문제 : https://www.acmicpc.net/problem/16964

풀이

문제로 주어진 그래프를 1부터 DFS로 탐색했을 때, 입력으로 주어지는 방문 순서가 올바른지 확인하는 문제이다.

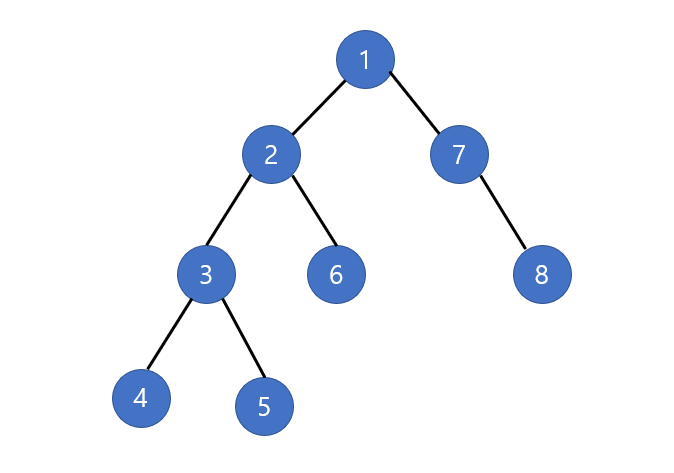
위와 같은 그래프가 있을 때 가능한 DFS 탐색 경우의 수를 일부 나열 하자면 다음과 같다.

• 1 2 3 4 5 6 7 8
• 1 2 4 3 5 4 7 8
• 1 2 6 3 4 5 7 8
• 1 2 6 3 5 4 7 8

• 1 7 8 2 3 4 5 6
• 1 7 8 2 6 3 4 5
• 1 7 8 2 3 5 4 6
• 1 7 8 2 6 3 5 4

굵은 글씨를 자세히보면 서로 형제관계에 있는 노드는 위치가 변하지 않는다는 것을 알 수 있다.
그리고 두 형제 노드 사이의 간격은 바로 먼저 나온 노드의 후손 수와 일치한다.

• 2의 경우 4개의 노드를 후손으로 갖고 있어 형제 노드인 7과의 간격이 4이다.
• 7의 경우 1개의 노드를 후손으로 갖고 있어 형제 노드인 2와의 간격이 1이다.

3, 6에서도 동일하게 적용된다.

• 1 2 3 4 5 6 7 8
• 1 2 6 3 4 5 7 8

3은 2개의 후손노드가 있어 6과의 간격이 2이고, 6은 자손이 없어 3과의 간격이 없다.

즉 입력 받은 순서에서 자신의 후손 수 만큼 떨어져있는 노드는 트리 깊이가 자신과 같다.

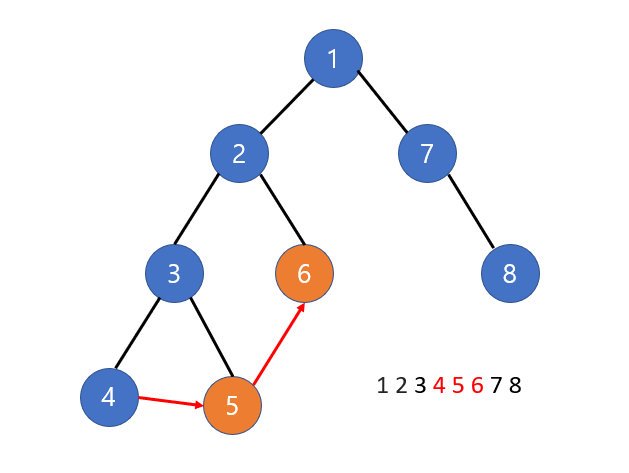
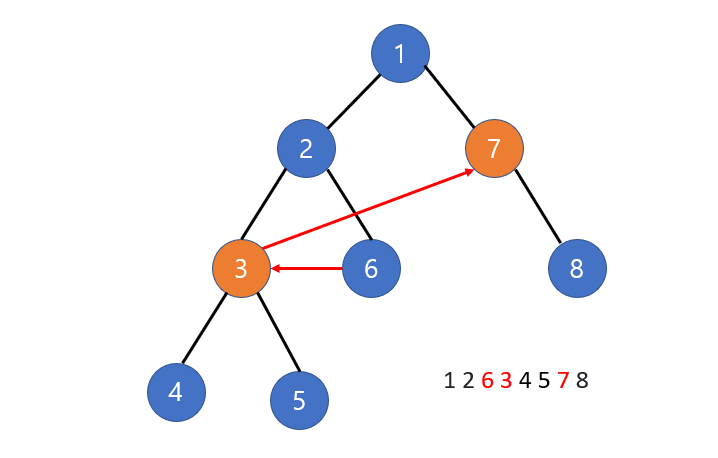
하지만 위와 같이 떨어져 있는 노드가 자신의 형제 노드가 아닌 경우가 있다.

이는 이미 앞서서 다른 형제노드를 먼저 방문해서 자신이 다음으로 방문할 형제 노드가 없기 때문이며, 이 경우 조상 노드의 형제 노드를 가리키게 된다

즉 올바른 DFS 탐색 순서라면 자신의 후손 수 만큼 떨어져있는 노드의 트리 깊이가 자기보다 깊은 경우는 없다

정리

1. 입력받은 그래프에 대해 DFS를 돌면서 각 노드의 후손 수와 트리 깊이를 구한다.
2. 주어진 배열에 대해 for문을 돌면서 자신의 후손 수 만큼 떨어져 있는 노드의 깊이가 자기보다 깊은지 확인한다.
   • 후손 노드의 트리 깊이가 더 깊은 경우 : 올바른 DFS가 아니므로 0을 출력하고 종료
   • 후손 노드의 트리 깊이가 같거나 얕은 경우 : 다음 순서로 이동
   • ※ 첫 순서는 무조건 1이어야 하므로, 첫 순서가 1이 아닐 경우 0을 출력하고 종료
3. 입력 된 순서를 모두 돌면, 문제가 되는 부분이 없으므로 1을 출력한다.

코드

날 것 그대로의 코드라 정리되지도 않았고 효율도 좋지 않습니다 참고만 해주세요

import sys
input = sys.stdin.readline


def DFS(L, node):
    if visited[node]:
        return 0
    visited[node] = True
    depth[node] = L
    for next_node in graph[node]:
        if not visited[next_node]:
            children[node] += DFS(L+1, next_node) + 1
    return children[node]


N = int(input())
graph = [[] for _ in range(N)]
children = [0] * N
depth = [0] * N
visited = [False] * N
for _ in range(N-1):
    a, b = map(int, input().split())
    graph[a-1].append(b-1)
    graph[b-1].append(a-1)

request = list(map(int, input().split()))

DFS(0, 0)

is_DFS = True

for i in range(N):
    if i == 0:
        if request[i] != 1:
            is_DFS = False
            break
        else:
            continue
    node = request[i]-1
    sibling = i+children[node]+1

    if sibling < N:
        sibling_node = request[sibling]-1
        if depth[sibling_node] > depth[node]:
            is_DFS = False
            break

print(1 if is_DFS else 0)