[백준] 11049. 행렬 곱셈 순서 (파이썬)

cjkangme·2023년 8월 5일

DP 알고리즘

Algorithm

목록 보기

32/35

문제 : https://www.acmicpc.net/problem/11049

문제 설명

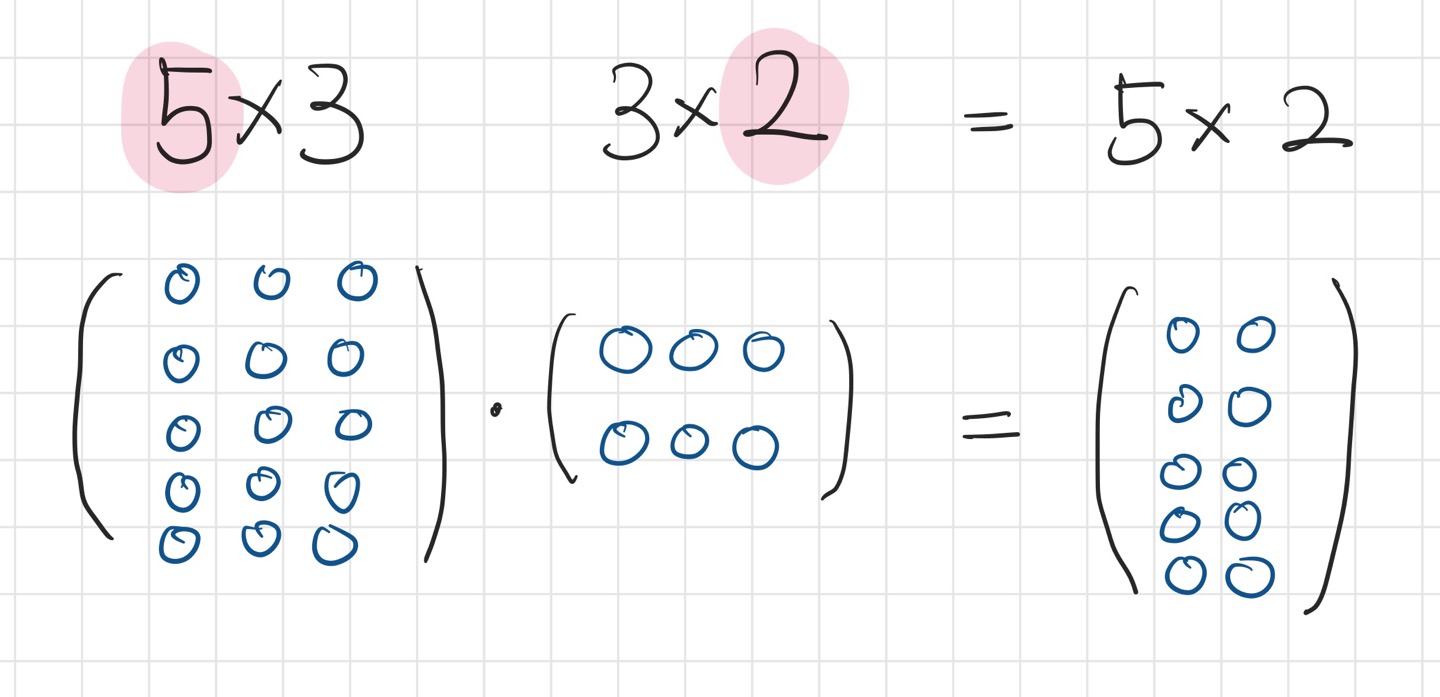
(N * M) 행렬과 (M * K) 행렬을 곱셈하면 (N * K) 행렬이 결과로 나오고
이 때 필요한 연산 횟수는 N * M * K 이다.

다만 3개 이상의 행렬을 곱셈할 때 곱셈하는 순서에 따라서 연산 횟수가 달라질 수 있다.

대표적으로 예제에 주어진 ABC행렬의 경우
1. (AB)C = 5×3×2 + 5×2×6 = 30 + 60 = 90번
2. A(BC) = 3×2×6 + 5×3×6 = 36 + 90 = 126번
이렇게 두가지 경우가 존재한다.

풀이

다이나믹 프로그래밍을 통해 풀 수 있다.

행렬 n개가 주어졌을 때 dp[i][j]는 i번 인덱스의 행렬부터 j번 인덱스의 행렬까지 곱셈했을 때의 최소 연산 횟수이다.

dp[0][0]은 행렬 자기 자신이므로 연산이 필요 없어 dp[i][i] = 0이 되고
dp[0][1]은 이웃한 행렬끼리 연산한 것이다.
dp[0][n]이 문제에서 출력해야할 최종 답안이 된다.

예제

행렬이 4개 주어졌다고 가정하면 다음과 같다.

dp[0][4]를 구하기 위해서는 위와 같이 3가지 경우의 수를 각각 구하고 최솟값을 취해야 한다.

즉 행렬을 서브 행렬로 쪼개어 각각의 최소 연산 횟수를 더한 것이다

이를 위해서는 dp[0][2]와 같은 값을 알아야 하는데

이렇게 작은 단위로 쪼개는 것을 통해 구할 수 있다.

구현

# 다이나믹 테이블 초기화
dt = [[INF] * N for _ in range(N)]
    
# 점화식을 위한 초기값 세팅
for i in range(N):
    dt[i][i] = 0

먼저 최솟값을 구해야하므로 INF로 리스트를 선언 한 뒤 dp[i][i]를 0으로 초기화 해준다.

for i in range(1, N):
  for j in range(N-i):
    for k in range(j, j+i):
      temp = dt[j][k] + dt[k+1][j+i] + (arr[j][0] * arr[k][1] * arr[j+i][1])
      dt[j][j+i] = min(dt[j][j+i], temp)

3중 for문을 통해 위 로직을 구현할 수 있다.

i는 dt를 구할 범위(윈도우)를 지정한다.
i=1이라면 dt[0][1], dt[2][3]과 같은 값을 구하는 것이고
i=3이라면 dt[0][3] 을 구하는 것이다.

j는 구하고 싶은 dt의 시작 인덱스를 나타낸다.

k는 서브행렬로 쪼갤 기준점을 나타낸다.

아까 사진을 다시 들고왔는데

여기서 i=3, j=0, k=[0, 1, 2] 를 나타낸다.

이를 통해 dt[j][j+i] 의 값을 구할 수 있다.

최종 코드

import sys

input = sys.stdin.readline
INF = 2 ** 31

if __name__=="__main__":
    N = int(input())
    arr = [tuple(map(int, input().split())) for _ in range(N)]
    dt = [[INF] * N for _ in range(N)]
    
    # 점화식을 위한 초기값 세팅
    for i in range(N):
        dt[i][i] = 0
    
    # 다이나믹 프로그래밍 탐색
    for i in range(1, N):
        for j in range(N-i):
            for k in range(j, j+i):
                temp = dt[j][k] + dt[k+1][j+i] + (arr[j][0] * arr[k][1] * arr[j+i][1])
                dt[j][j+i] = min(dt[j][j+i], temp)

    print(dt[0][N-1])