문제
아래의 표를 만족하는 정수 수열을 구하는 문제이다.
수열 a의 길이가 n일 때 n행 n열 크기의 표가 주어진다.
| 표 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | - | + | 0 | + |
| 2 | + | + | + | |
| 3 | - | - | ||
| 4 | + |
위 표가 의미하는 것은 다음과 같다.
1행 3열 -> a1 부터 a3까지 합한 값이 0이다.
1행 4열 -> a1 부터 a4까지 합한 값이 양수이다. (0보다 크다)
3행 4열 -> a3 부터 a4까지 합한 값이 음수이다. (0보다 작다)
즉, am부터 an까지 합한 값이 표의 m행 n열의 부호와 같아야 한다.
출력조건
답은 여러개가 존재할 수 있으며, 그 중 하나를 출력하면 된다.
수열의 모든 값은 -10 이상, 10 이하의 정수이다.
풀이
백트래킹 알고리즘을 이용해 풀 수 있다.
백트래킹이란, 우선 값을 대입해 본 뒤, 대입한 값이 정답이 아니라면 되돌아가서 다음 값을 대입해 보는 것이다.
DFS를 돌면서 현재 값이 답이 아닐 때, 더 이상 가지를 뻗지 않고 return 한다면 백트래킹 알고리즘이 된다.
알고리즘
부호 변환
기본적으로 0번 인덱스부터 시작하여, 인덱스가 n에 도달하면 종료하는 DFS로 문제풀이를 진행한다.

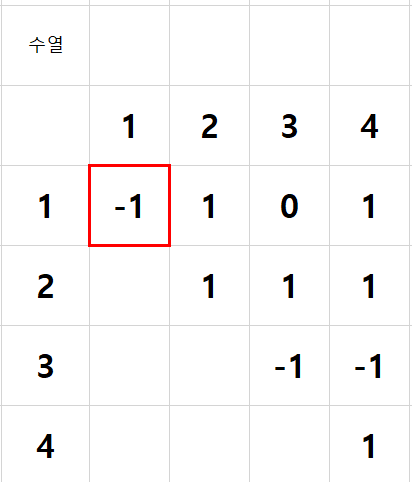
우선 input으로 받은 부호를 계산 편의를 위해 정수형으로 변환해준다.
답이 될 수 있는 범위는 -10 이상, 10 이하인데, 부호를 정수형으로 변환하면 비교 및 for문 처리가 쉬워진다.
1번 인덱스

수열의 값 범위는 -10 ~ 10 이므로, 범위 중에서 가능한 수는 다음과 같다.
-1, -2, -3, -4, -5, -6, -7, -8, -9, -10
for문을 통해 이들 숫자를 모두 대입한다.
가장 먼저 -1이 선택된다.
2번 인덱스
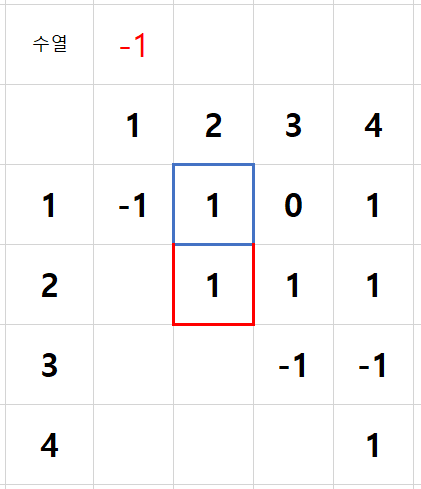
먼저 빨간색 테두리는 a2 값이 0보다 커야한다는 것을 의미한다.
즉 가능한 수는 다음과 같다.
a2: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
그 다음으로 파란색 테두리는 a1 + a2 값이 0보다 커야한 다는 것을 의미한다.
여기서 a2 = 1 일 경우, a1 + a2 = 0 이 되면서 조건을 만족하지 못하므로, a2 = 1을 대입한 경우는 더 이상 진행하지 않고 return한다. (백트래킹)
파란색 테두리
a2: 2, 3, 4, 5, 6, 7, 8, 9, 10
3번 인덱스
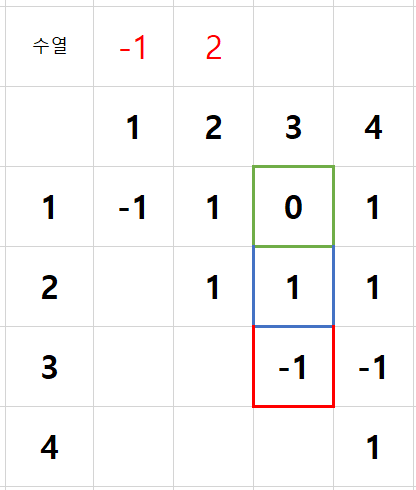
빨간색 테두리에 의해 a3 값이 0보다 작아야하므로 가능한 수는 다음과 같다.
a3: -1, -2, -3, -4, -5, -6, -7, -8, -9, -10
파란색 테두리는 a2 + a3 값이 0보다 커야함을 의미하므로 가능한 수는 다음과 같다.
a3: -1
초록색 테두리는 a1 + a2 + a3 = 0임을 의미하므로 가능한 수는 다음과 같다.
a3: -1
4번 인덱스
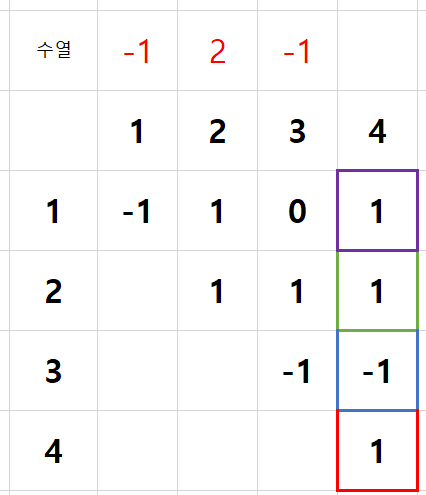
같은 방식으로 계속 적용을 진행한다.
빨간색 테두리
a4: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
그런데 파란색 테두리에서 a3 + a4 < 0 을 만족하는 a4가 존재하지 않는다.
이 수열은 정답이 아니므로 다시 3번 인덱스로 백트래킹을 하게 된다.
3번 인덱스 - 2
빨간색 테두리
a3: -1, -2, -3, -4, -5, -6, -7, -8, -9, -10
위 경우의 수 중 -1은 백트래킹으로 제외되었고, 다음으로 -2가 선택된다.
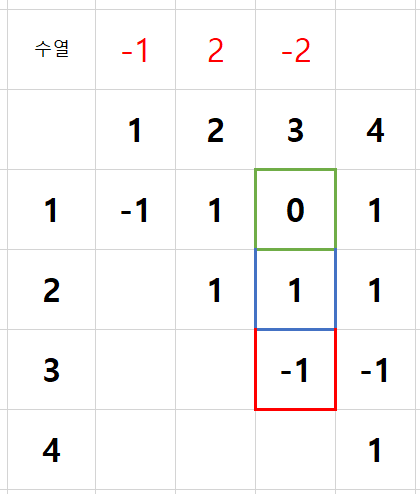
그런데 이번에도 파란색 테두리에서 a2 + a3 > 0 을 만족하는 값이 존재하지 않는다.
이 수열도 정답이 아니므로 2번 인덱스로 백트래킹을 한다.
2번 인덱스 - 2
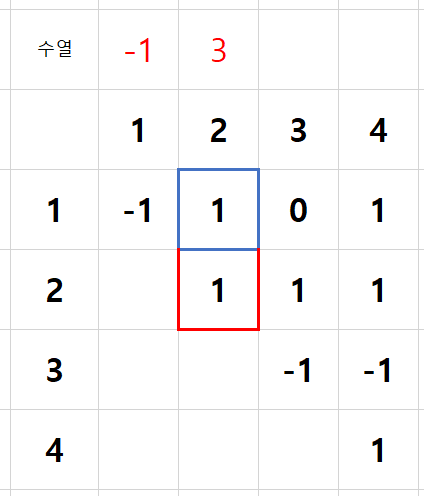
파란색 테두리에서 만족한 범위는 2 ~ 10이므로 이곳에서 부터 시작하면 된다.
a2: 3, 4, 5, 6, 7, 8, 9, 10
2는 백트래킹으로 돌아오게 되었으므로 제외하고, 3을 선택한다.
3번 인덱스 - 3
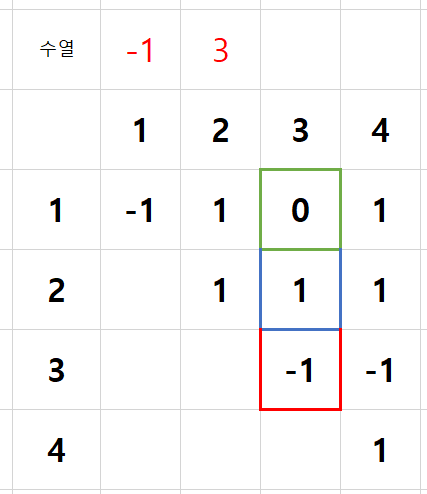
동일한 알고리즘으로 가능한 수를 선택한다.
빨간색 테두리
a3: -1, -2, -3, -4, -5, -6, -7, -8, -9, -10
파란색 테두리
a3: -1, -2
가능한 값이 2개인데, 지금까지와 마찬가지로 먼저 -1을 선택한다.
파란색 테두리에서 -1을 선택한경우 초록색 테두리에서 거짓이 된다. (a1 + a2 + a3 = 1)
다시 파란색 테두리로 백트래킹 한 뒤에 -2를 선택하면 참이 되어 다음으로 진행할 수 있다.
a3: -2
4번 인덱스 - 2
설명은 생략하지만, 동일한 알고리즘으로 a4 = 1이 가능함을 도출할 수 있다.

이상태로 다음 DFS로 진행되면 <DFS의 깊이> = n이 되며, 출력 후 함수를 종료하면 된다.
코드
import sys
def check(idx, num):
answer[idx] = num
temp = 0
for i in range(idx, -1, -1):
temp += answer[i]
if sign_matrix[i][idx] > 0 and temp <= 0:
return False
elif sign_matrix[i][idx] < 0 and temp >= 0:
return False
elif sign_matrix[i][idx] == 0 and temp != 0:
return False
return True
def DFS(L):
if L == n:
print(*answer)
sys.exit(0)
else:
if sign_matrix[L][L] == 0:
if check(L, 0):
DFS(L+1)
else:
for x in range(1, 11):
xx = x * sign_matrix[L][L]
if check(L, xx):
DFS(L+1)
if __name__ == "__main__":
n = int(input())
S = input()
sign_matrix = [[None] * n for _ in range(n)]
answer = [0] * n
pointer = 0
for i in range(n):
for j in range(i, n):
if S[pointer] == '+':
sign_matrix[i][j] = 1
elif S[pointer] == '-':
sign_matrix[i][j] = -1
else:
sign_matrix[i][j] = 0
pointer += 1
DFS(0)코드 설명
input
2차원 리스트 sign_matrix를 만들어 부호를 저장한다.
2차원 리스트이지만, 입력값이 한 줄로 주어지므로 별도의 처리가 필요하다.
-
우선 문자열을 한번에 입력 받는다.
-
pointer라는 변수를 만들어 0부터 n(n+1)/2까지 1씩 증가하며 문자열 index를 가리키도록 한다.
입력의 수가 n(n+1)/2개이므로, 그냥 1씩 증가시키면서 2중 for문을 돌면 된다. -
2중 for문을 돌면서 입력값이
'-'이면-1로,'+'이면1로, 나머지는0으로 저장한다.
DFS 함수
-
DFS의 깊이가
n에 도달하면 함수 출력후 프로그램을 종료하도록 한다.
sys.exit(0)이 프로그램을 즉시 종료하는 함수이다. -
sign_matrix[L][L]이answer[L]의 부호를 나타내므로, 이 값이 0이면 해당 값만 검사하면 된다, -
0이 아니라면 1~10 범위의 for문을 돈다.
sign_matrix에 1 또는 -1이 저장되어 있으므로,range(1,11)에 부호를 곱해주면 된다.
check 함수
현재 수열이 정답 조건을 만족하는지 아닌지 체크하는 함수이다.
for 문이 각 테두리를 검사한다.
- 문제의 조건을 조건문으로 구현하여, 정답이 아닌 조건이라면 False를 반환하고 함수를 빠져나온다. (백트래킹)
- 모든 반복문을 통과하면 정답조건을 만족했다는 뜻이므로 True를 반환한다.
다음 DFS
check함수에서 True를 반환 받았을 때만 가지를 뻗어야 하므로 if 문으로check함수의 반환값이 True일 때 다음 깊이의DFS함수를 호출한다.

