정석 풀이가 아닐 수 있습니다.
문제 요약
-
팰린드롬 : '회문'과 같은 말로, 뒤집어도 처음과 똑같은 수열을 가리키는 말이다.
-
1 2 3 4 2에 최소의 숫자를 추가해서 팰린드롬을 만드는 문제이다. -
이 경우 4와 2 사이에 3을, 2 다음에 1을 추가하여
1 2 3 4 3 2 1을 만들 수 있다. (추가한 숫자 2개)
풀이
- 다이나믹 프로그래밍을 이용하여 풀 수 있다.
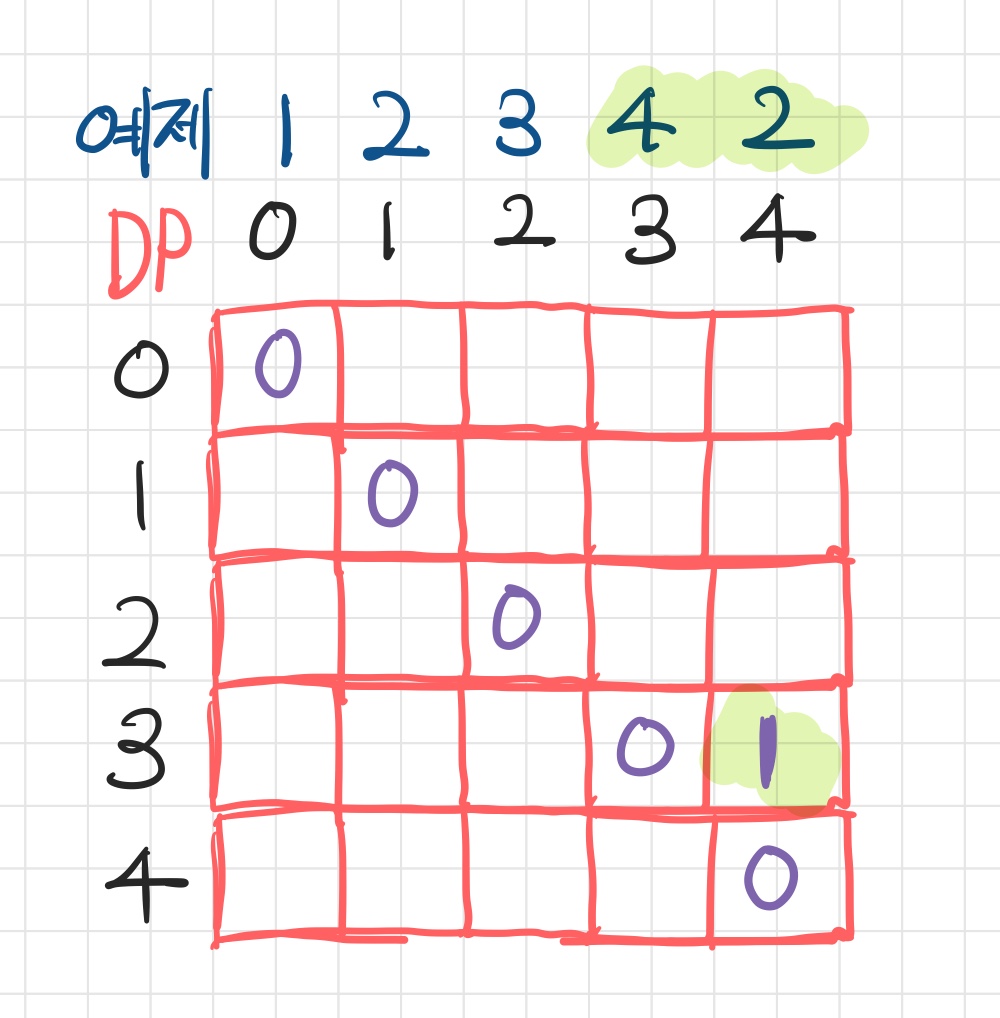
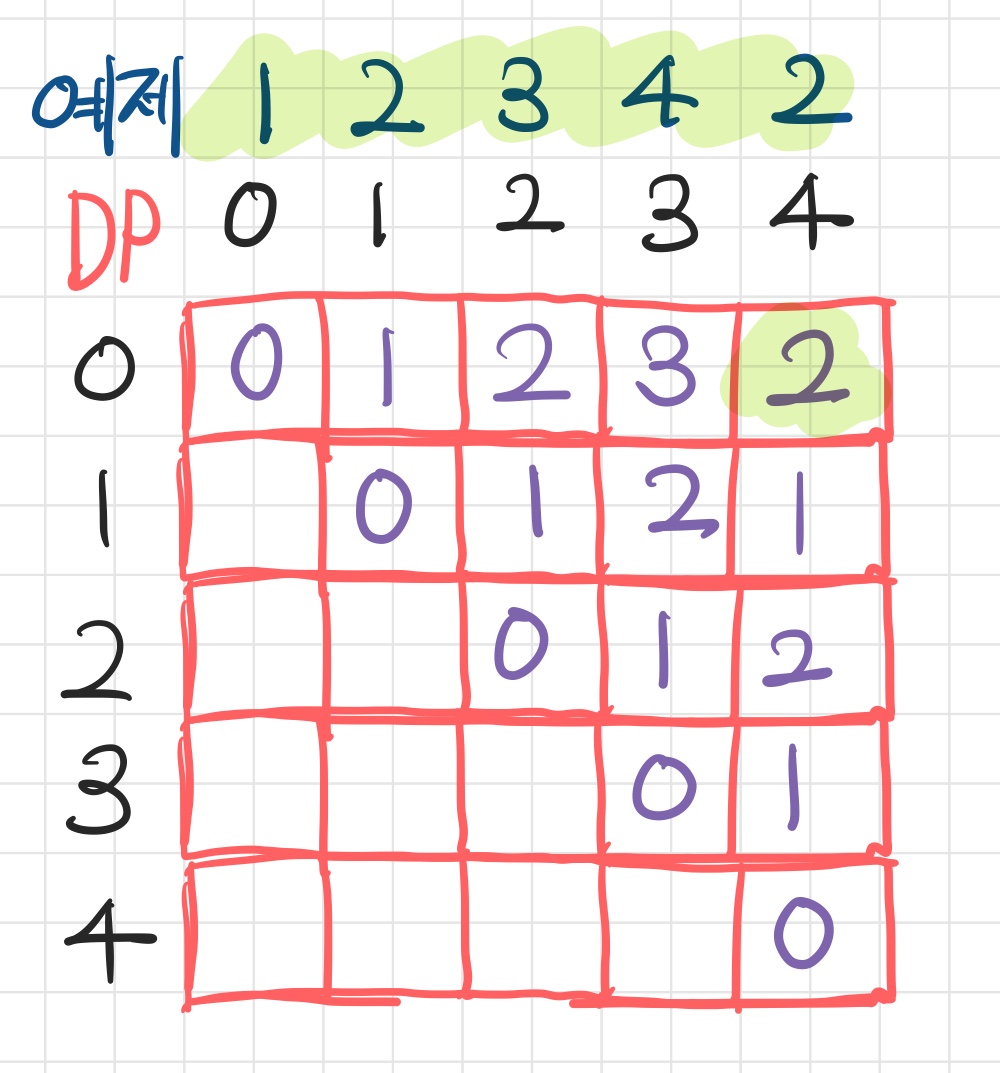
DP[i][j]는 i번째 글자부터 j번째 글자까지를 팰린드롬으로 만들기 위해 끼워넣어야 하는 수의 개수이다.- 가령
DP[3][4]는4 2를 팰린드롬으로 만들기 위해 필요한 수이며, 이 경우 오른쪽 끝에 2를 끼워넣거나, 왼쪽 끝에 2를 끼워 넣어 1임을 알 수 있다. - 이처럼 수열 길이가 2이고 서로 다른 수일 경우
DP[i][i+1]의 값은 1이된다.
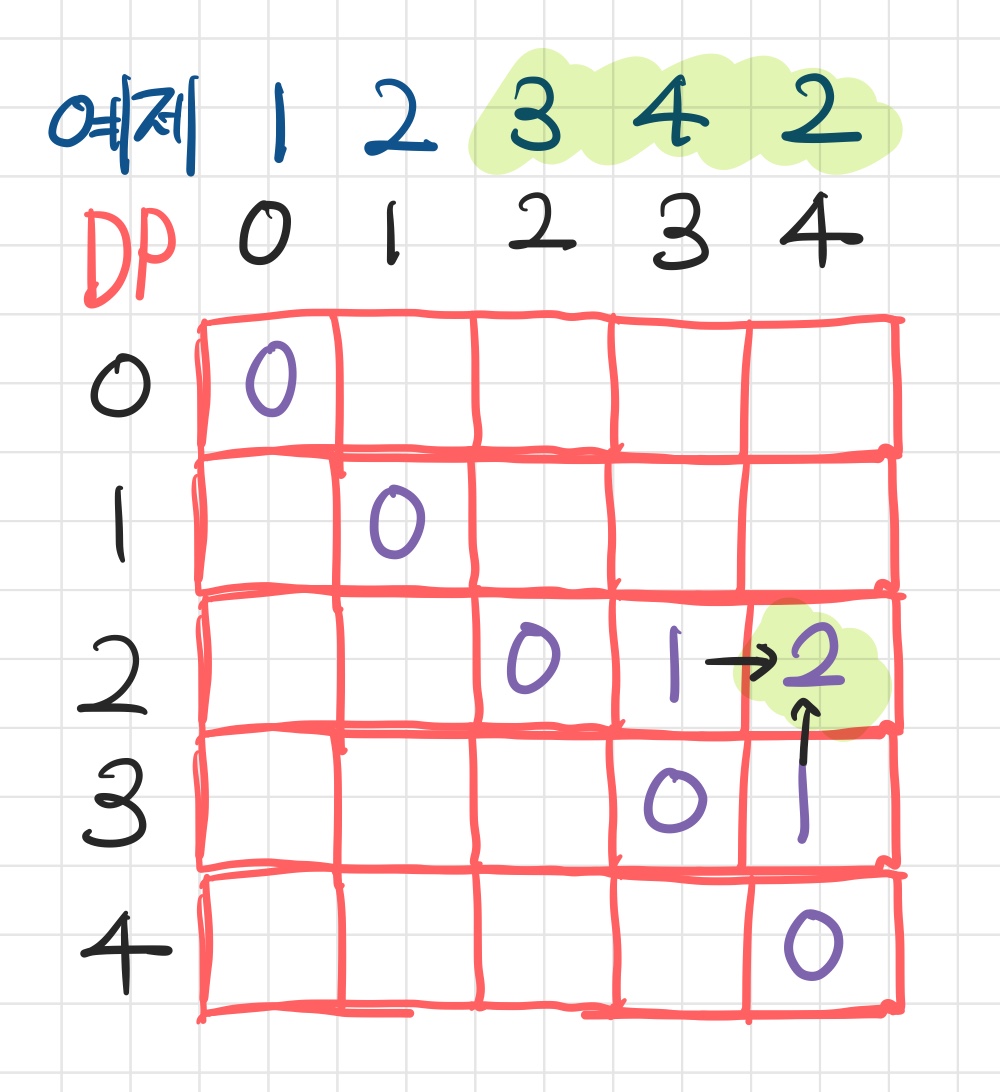
- 다이나믹 테이블을 채워나가다가
DP[2][4]를 마주하였을 때의 경우이다. - 결론만 말하자면
DP[i][j-1]과DP[i+1][j]값의 최소값을 구하여 여기에 1을 더한 숫자가DP[i][j]의 값이 된다.

- 이유를 조금 풀어서 설명하자면,
DP[2][4]는DP[2][3], DP[4]또는DP[2], DP[3][4]로 쪼개어 생각할 수 있다. - 이들은 이미 다이나믹 테이블이 알고 있는 값이며, 숫자를 1개(빨간색 숫자)만 추가하면 팰린드롬이 된다는 것이 확실하다. (
2 3 2또는3 4 3) - 이제 우리가 풀고자 하는
DP[2][4]는 팰린드롬의 한쪽 끝에 숫자 하나를 추가한 꼴이 된다. (2 3 2 4또는2 3 4 3) - 이제 여기에 반대쪽 끝에 같은 수를 추가하면 팰린드롬이 되므로 +1을 하면 된다.
- 최소로 추가하도록 DP 값을 구해야 하므로
DP[i][j-1]과DP[i+1][j]중 최소값을 취하여 1을 더하면DP[i][j]의 값이 된다.
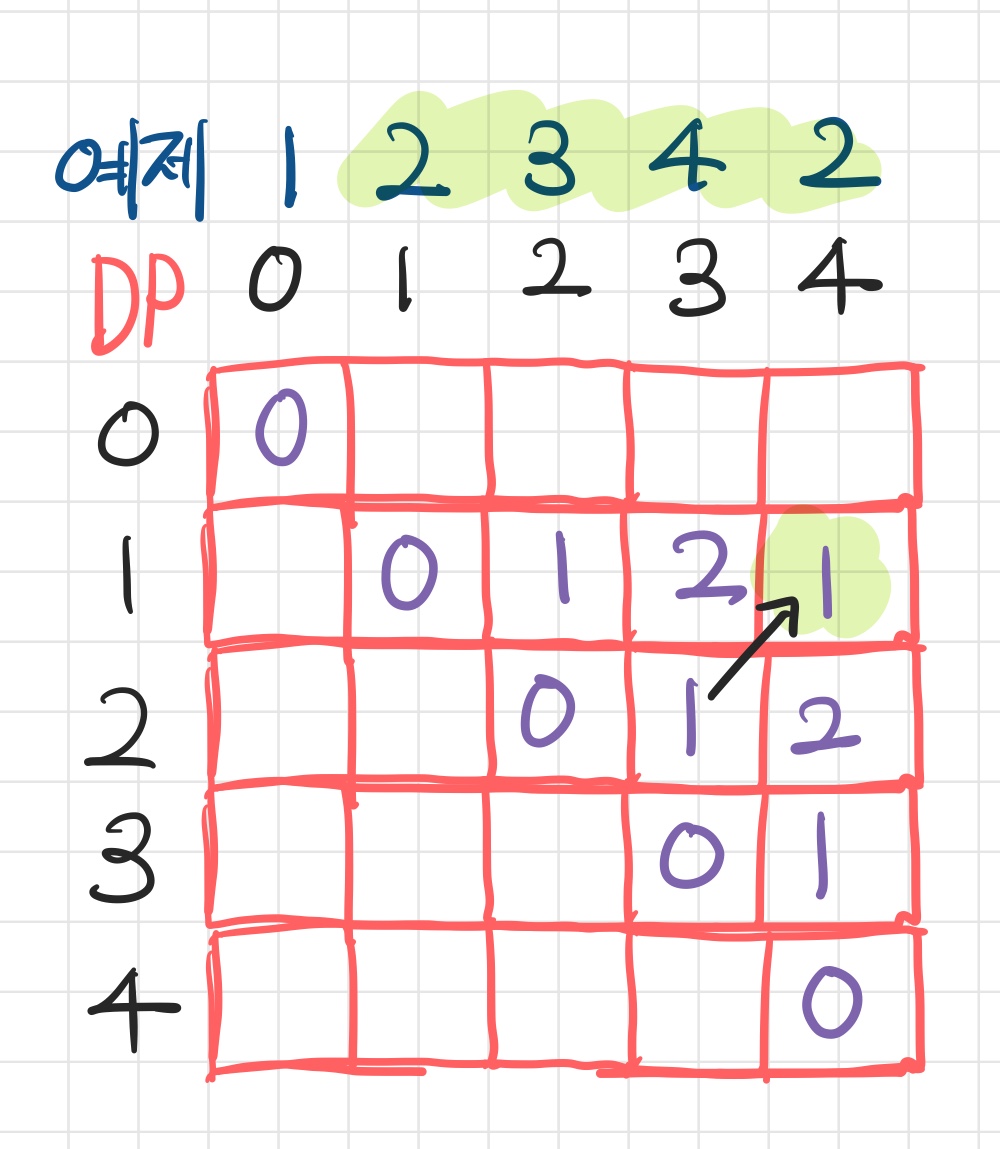
- 이번엔 새로운 경우인데 바로
DP[i][j]에서arr[i]==arr[j]인 경우이다. - 마찬가지로 결로만 말하면
DP[i+1][j-1]의 값이 그대로DP[i][j]값이 된다.
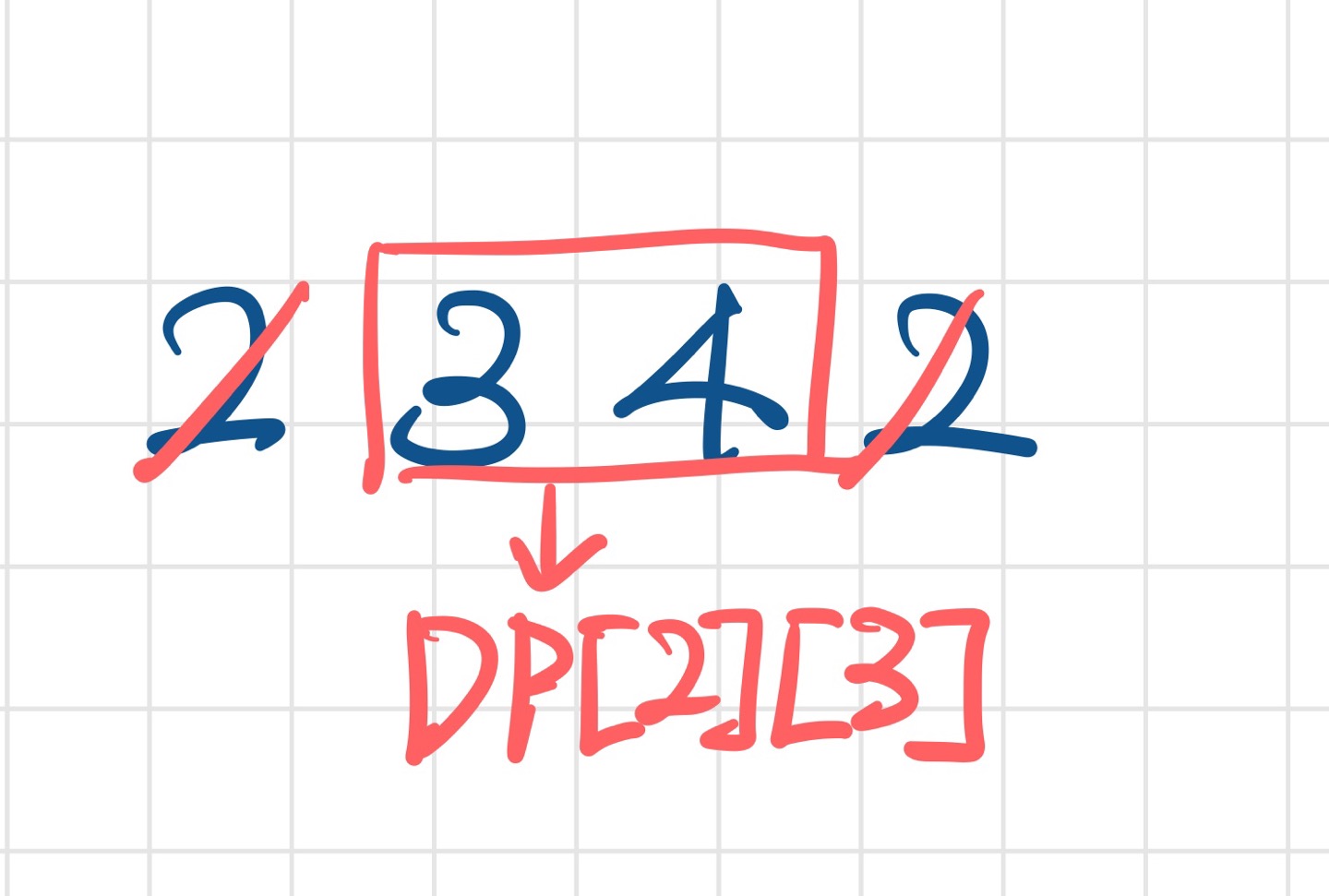
- 그 이유는 팰린드롬을 만들 때 양쪽 끝이 같기 때문에, 그냥 소거해 버릴 수 있고 결과적으로 i+1 부터 j-1 까지의 수열을 팰린드롬을 만드는 문제가 된다. 이는 이미
DP[i+1][j-1]이 알고 있으므로 그냥 값을 가져오면 된다.
- 같은 규칙을 적용하여
DP[0][-1]을 구했다면, 이것이 전체 수열을 팰린드롬으로 만들기 위해 추가해야할 수이다.
코드
-
풀이는 (N, N) 크기 이차원 행렬로 했지만 사실 (2, N) 크기의 행렬만 있어도 가능하다.
-
그 이유는 어짜피 정답은
DP[0][-1]으로 고정되어 있고, 한번에 봐야하는 행이 i와 i+1 2개이기 때문이다.
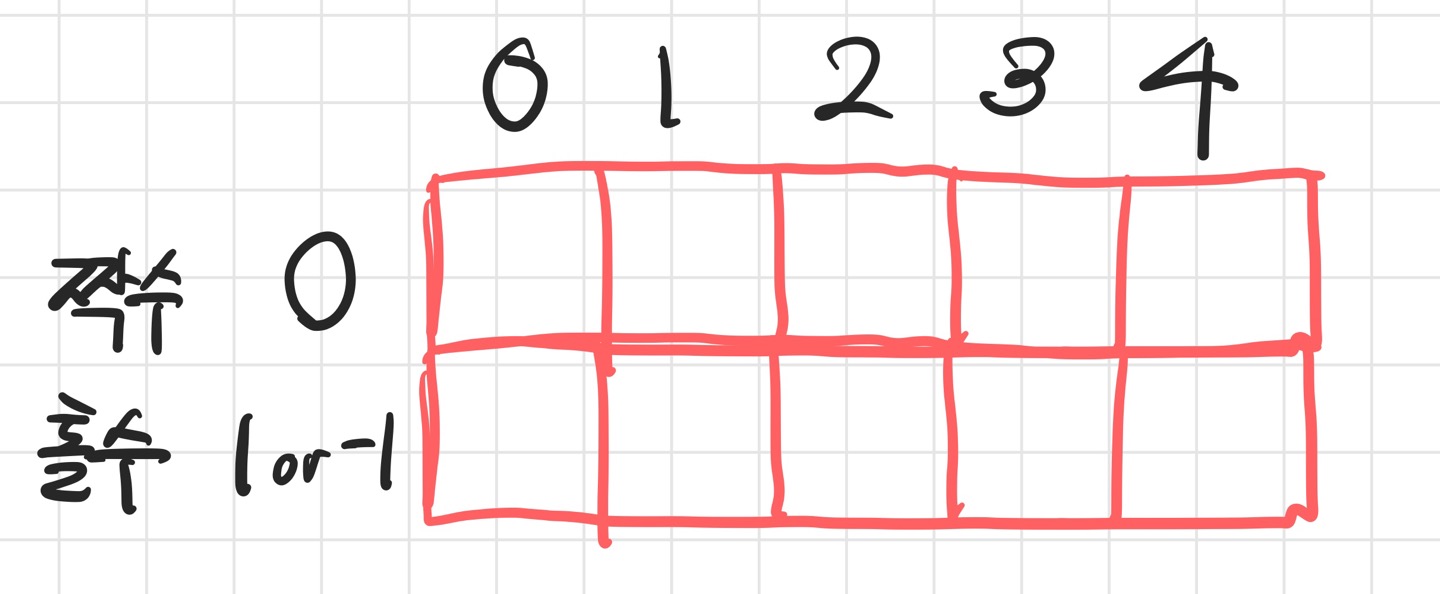
- 이렇게 행 인덱스가 짝수일 때 사용할 행과, 홀수일 때 사용할 행만 있으면 된다. 자세한 것은 코드로 확인하자.
import sys
input = sys.stdin.readline
N = int(input())
arr = list(map(int, input().split()))
dp = [[0] * N for _ in range(2)]
# 뒷부분부터 탐색해야함
for i in reversed(range(N)):
for j in range(i+1, N):
# 짝수와 홀수 구분
row = i % 2
# 홀수행(i=1)일 때 i-1=0으로 짝수행을 가리킴, 짝수행(i=0)일 때 i-1=-1로 홀수행을 가리킴
if arr[i] == arr[j]:
dp[row][j] = dp[row-1][j-1]
else:
dp[row][j] = min(dp[row][j-1], dp[row-1][j]) + 1
