풀이
- 주어진 종류의 동전을 무제한으로 사용해서 k원을 만들 수 있는 경우의 수를 출력하는 문제이다.
- 기본적으로 동적 계획법(DP)문제이지만, 다이나믹 테이블을 한 번 순회하고 끝나는 것이 아니라 동전의 종류 수만큼 순회해야 한다.
- 2원, 3원, 5원 동전 순으로 입력이 주어졌고, 입력된 순서대로 처리한다고 가정하자.
- 만들고자 하는 금액은 15원이다.
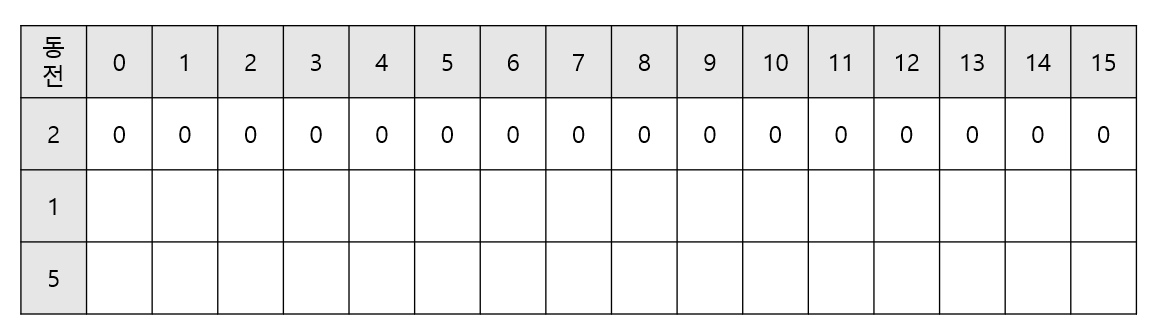
2원
- 다음과 같은 다이나믹 테이블을 만들 수 있다.
- 테이블의 i열 값은 i원을 만들 수 있는 경우를 뜻한다.
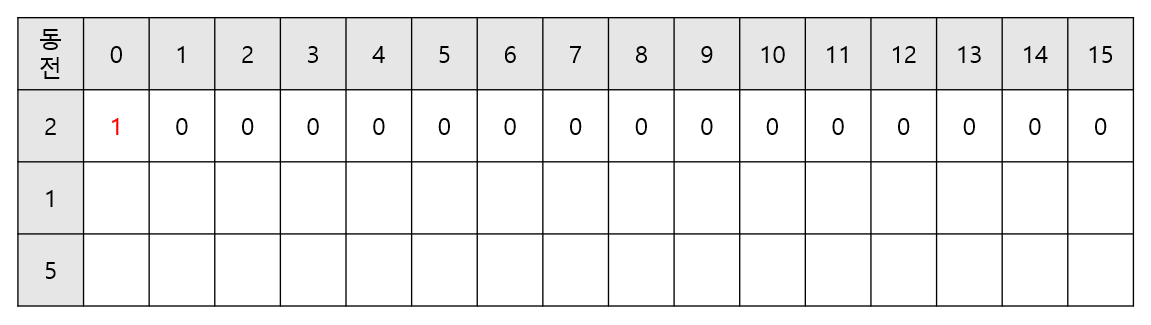
- 가장 먼저 0원을 만드는 경우의 수는 동전을 사용하지 않는 것 한가지이다.
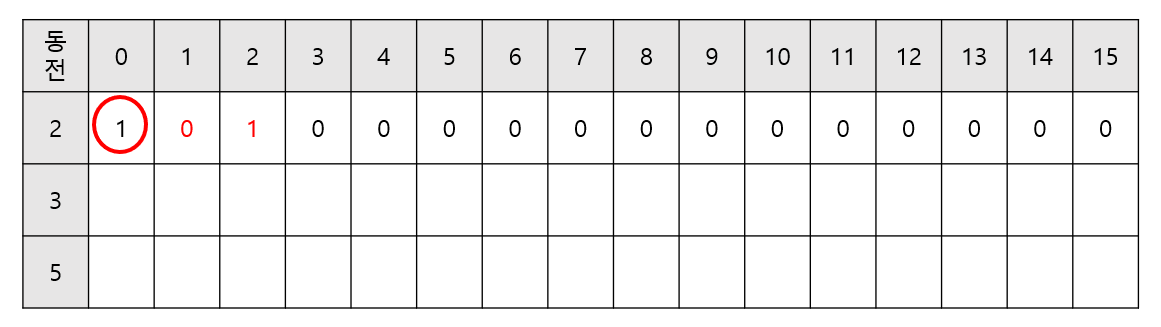
- 2원짜리 동전으로 1원을 만들순 없지만, 대신 0원에서 2원을 추가하여 2원을 만드는 것이 가능하다. 하지만 오직 2원 동전만 사용할 수 있으므로 경우의 수는 여전히 1이다.
- 이런식으로 15원까지 다이나믹 테이블을 채운다.
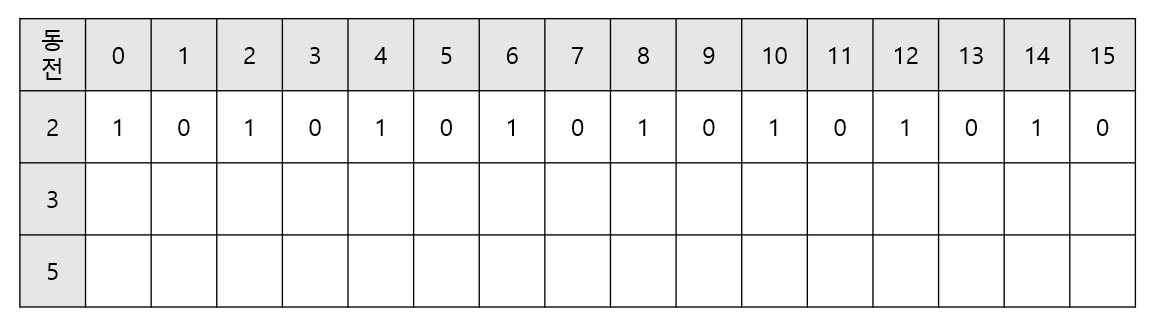
3원
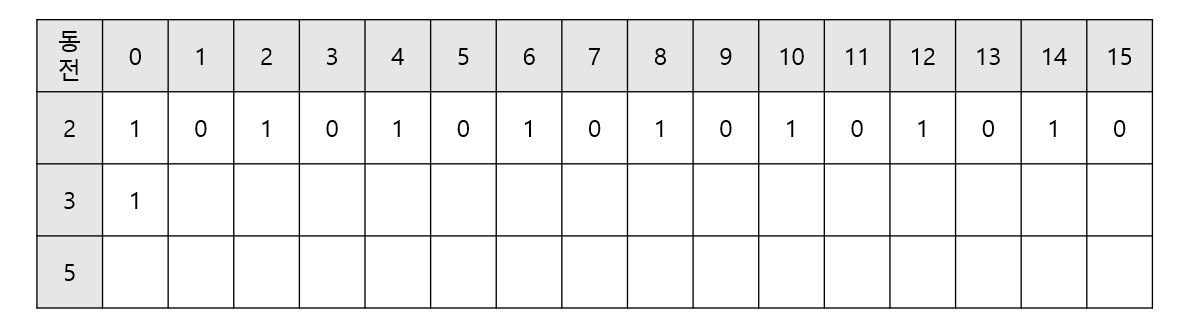
- 동일하게 0원, 경우의 수 1부터 출발한다.
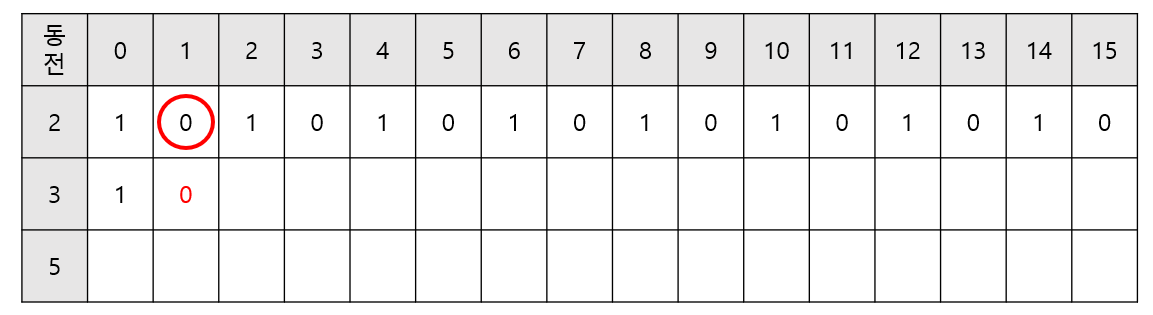
- 다음으로 1원인데, 3원으로 1원을 만들 수 없다. 또한 앞서 2원을 사용한 경우에도 1원을 만들 수 없으므로 경우의 수는 그대로 0이 된다.
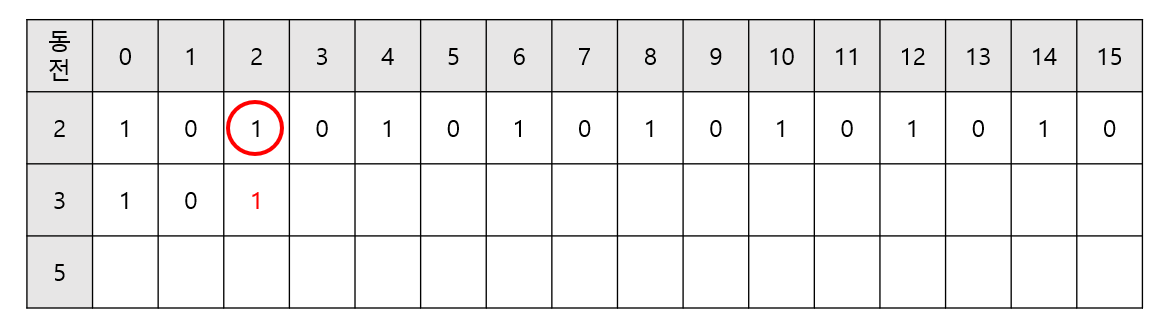
- 2원에서는 여전히 3원으로 만들 수 없다. 하지만 2원에서 1원을 만들 수 있는 경우가 있으므로 2원을 만드는 경우의 수는 1이다.
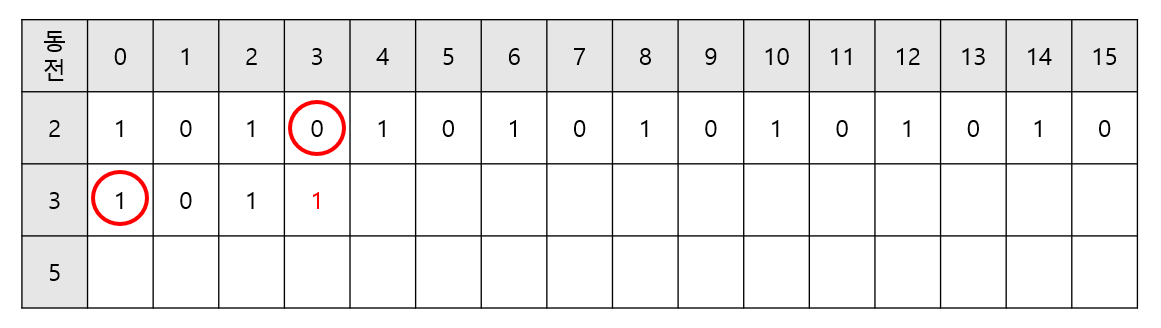
- 3원의 경우 0원에서 3원 동전 하나를 더해 만들 수 있다. 그러나 2원으로는 만들 수 있는 경우의 수가 없어 경우의 수는 1 + 0 = 1이다.
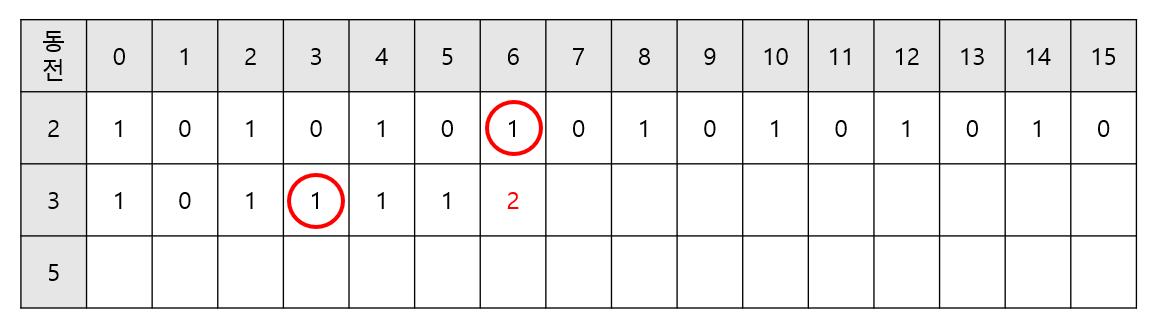
- 조금 건너 뛰어서 6원의 경우는 3원에서 3원 하나를 더해 6원을 만드는 경우의 수, 2원으로 6원을 만드는 경우의 수를 더하여 2가지의 경우의 수가 있다.
- 즉 k원의 가치가 있는 i번째 동전으로 j원을 만드는 경우의 수는
dy[i][j-k] + dy[i-1][j]라고 할 수 있다. - 동일한 방법으로 테이블을 모두 채워나간다.
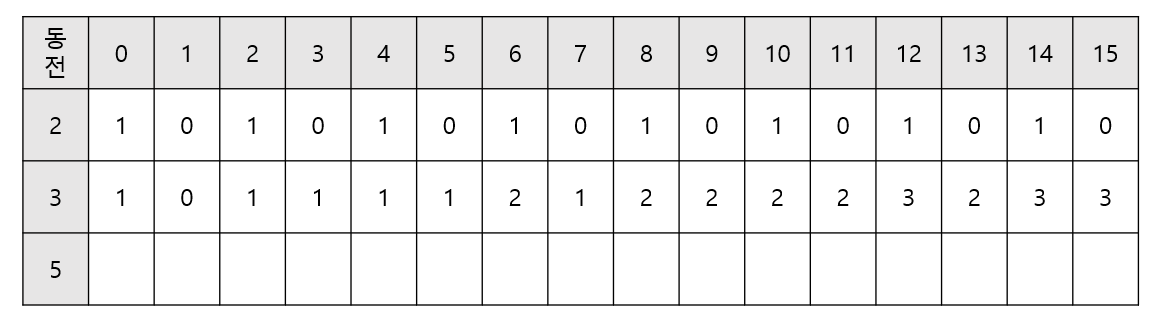
5원
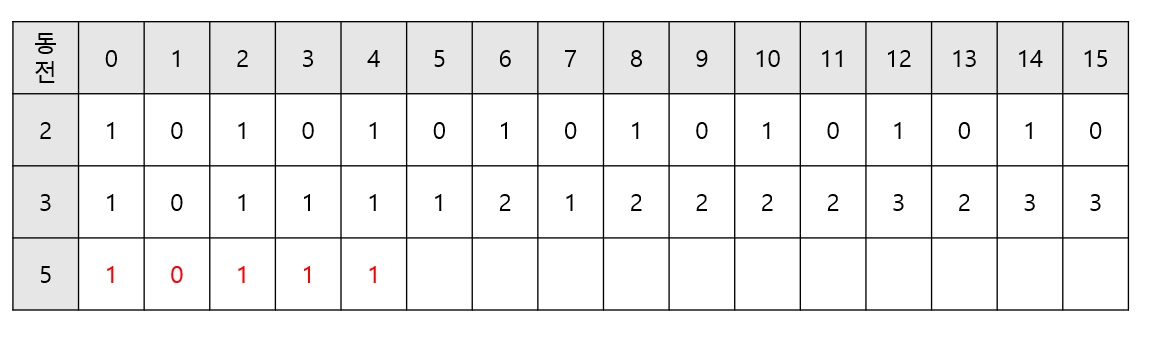
- 0원 ~ 4원까지는 5원으로 만들 수 있는 방법이 없어 3원까지 고려한 경우의 수와 동일하다.
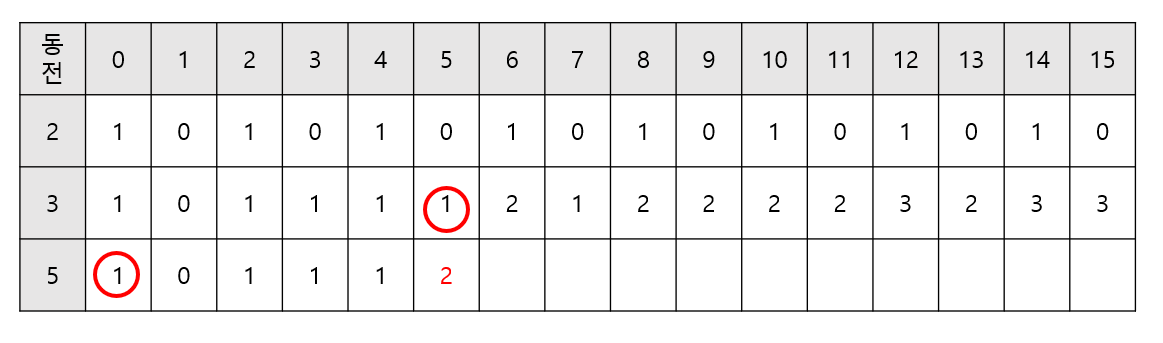
- 5원부터 다시 동일한 과정을 적용하면 된다.
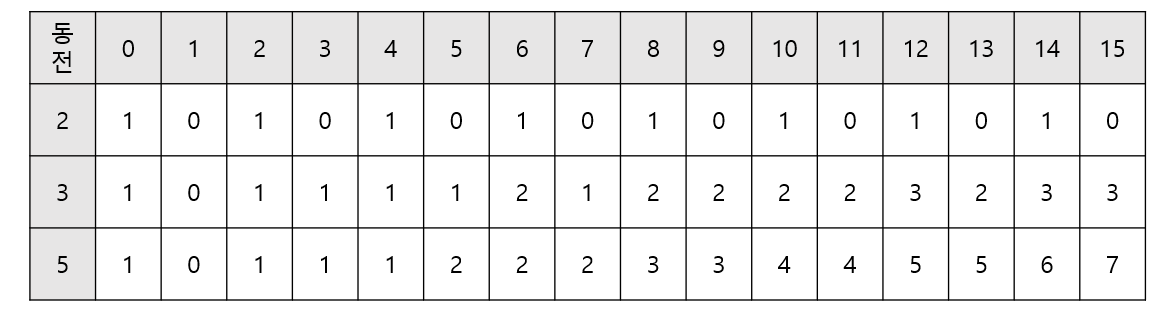
- 2, 3, 5원 모든 동전을 고려했을 때 15원을 만들 수 있는 방법은 7가지이다.
공간 복잡도 줄이기
- 위의 풀이 방법이라면 동전이 n 종류, 만들고자 하는 금액이 m원일 경우 (n+1) * m의 이차원리스트가 필요하다.
- 하지만 사실 n+1 길이의 1차원 리스트만 있으면 된다.
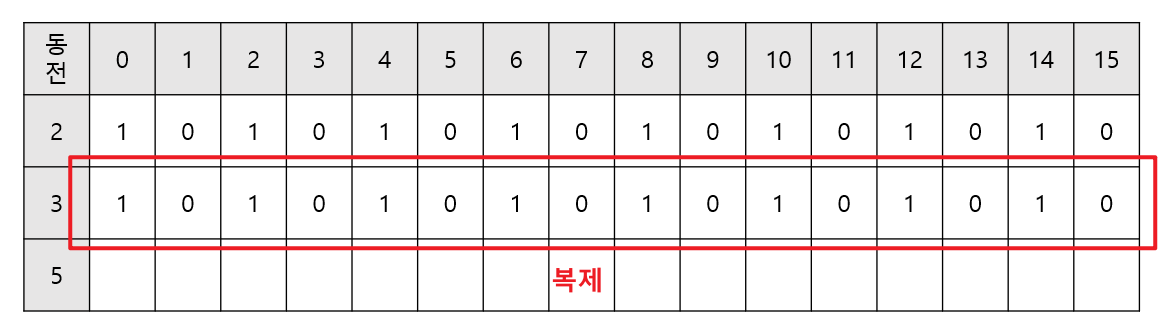
- 바로 위와 같이 리스트를 복제하고 순차적으로 for loop를 돌면
dy[j] = dy[j-k] + dy[j]로 나타낼 수 있기 때문이다.- 즉 실제로는 복제할 필요도 없이 하나의 일차원 리스트에서 누적합을 구하면 된다.
코드
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
coins = []
for _ in range(n):
coins.append(int(input()))
# 다이나믹 테이블을 생성하고 0번째 인덱스를 1로 지정
dy = [0] * (k+1)
dy[0] = 1
# 코인 종류별로 다이나믹 데이블 순회
for coin in coins:
for i in range(coin, k+1):
dy[i] += dy[i-coin]
print(dy[-1])코멘트
-
구현 자체는 전혀 어려운 문제가 아니지만, 다이나믹 테이블을 여러번 순회한다는 개념을 처음 접하여서 풀이에 상당한 애를 먹었다.
-
이러한 접근법도 있다는 것을 꼭 기억하자

