[백준] 2263. 트리의 순회 (파이썬)

cjkangme·2023년 7월 7일

알고리즘 파이썬

Algorithm

목록 보기

26/35

문제 : https://www.acmicpc.net/problem/2263

문제 요약

이진트리의 인오더(중위순회)와 포스트오더(후위순회) 순서가 주어졌을 때, 프리오더(전위순회)의 순서를 출력하는 문제이다.

주의할 점은 트리가 완전 이진트리가 아니라는 것이다.

※ 참고
전위 순회 : 부모 -> 왼쪽 자식 -> 오른쪽 자식
중위 순회 : 왼쪽 자식 -> 부모 -> 오른쪽 자식
후위 순회 : 왼쪽 자식 -> 오른쪽 자식 -> 부모

풀이

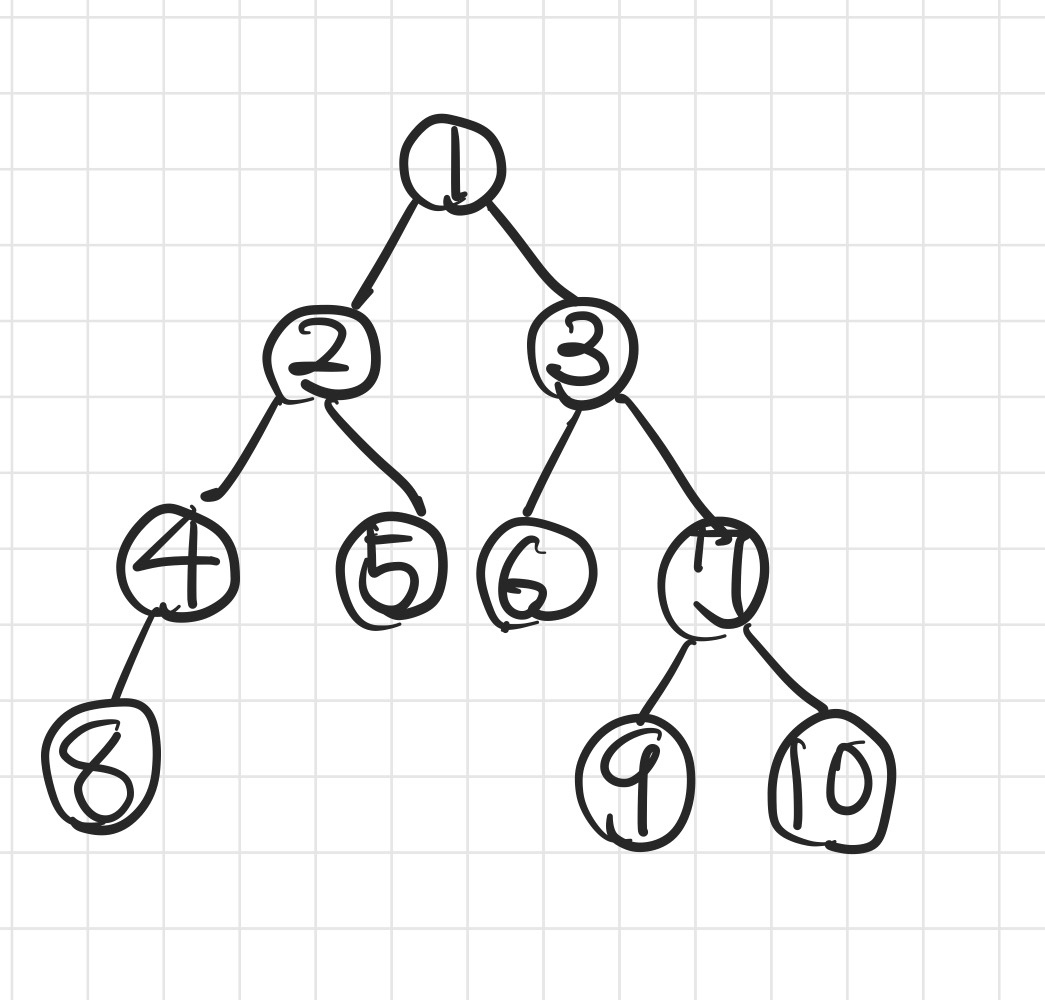
위와 같은 트리가 있을 때 주어지는 입력을 리스트로 만들면 다음과 같다.

중위 : [8, 4, 2, 5, 1, 6, 3, 9, 7, 10]
후위 : [8, 4, 5, 2, 6, 9, 10, 7, 3, 1]

루트 노드 찾기

여기서 후위 순위 리스트의 가장 마지막 원소는 항상 현재 트리의 루트 노드라는 것을 알 수 있다.

전위 순위에서는 부모 노드가 먼저 출력되므로 가장 먼저 이 루트 노드를 출력하면 된다.

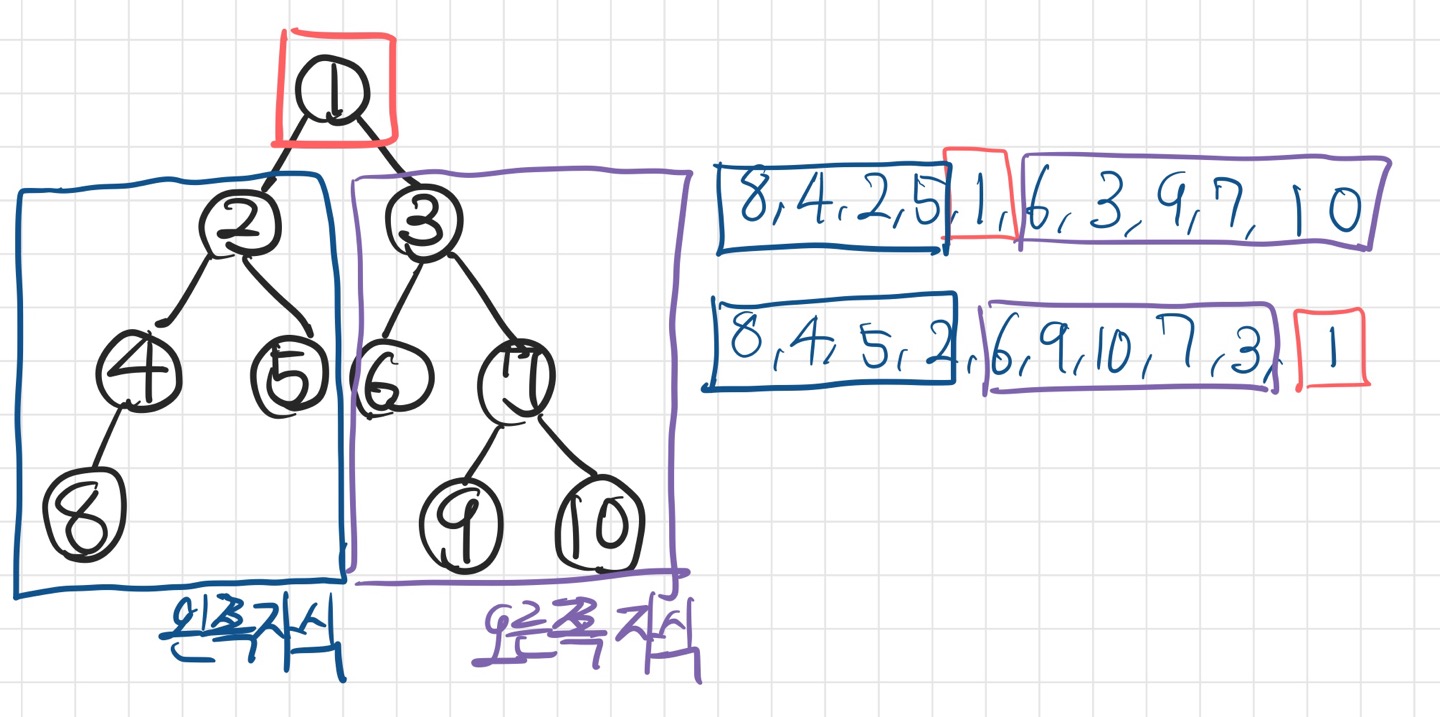
그리고 중위 순위 리스트에서 루트 노드 왼쪽의 원소들은 왼쪽 자식, 오른쪽의 원소들은 오른쪽 자식이라는 것도 알 수 있다.

왼쪽 자식 찾기

전위 순위에서 출력 순서는 부모 -> 왼쪽자식 -> 오른쪽자식이므로 찾아낸 왼쪽 자식에 대해 탐색을 진행한다.

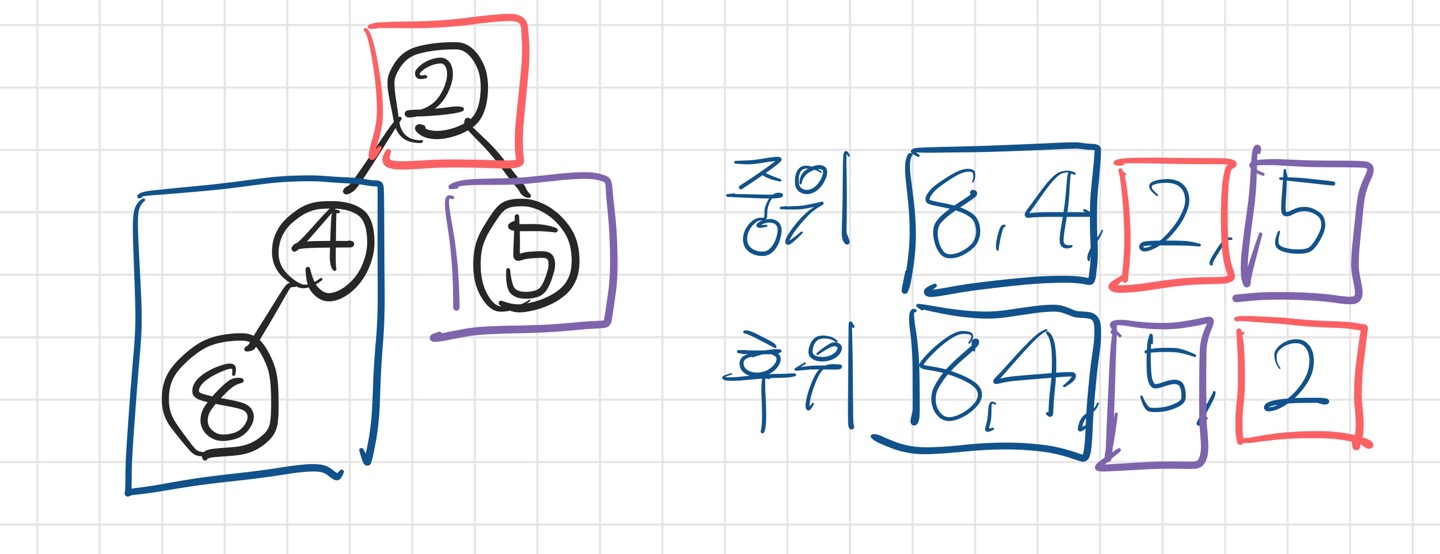
왼쪽 자식의 부분 트리에 대해서도 동일한 법칙이 적용된다.

후위 순위 리스트의 마지막 원소가 루트노드가 되며, 이를 출력한다.
중위 순위 리스트에서 루트노드의 왼쪽이 왼쪽자식, 오른쪽이 오른쪽 자식이 된다.

이를 원소가 하나 남을 때까지 반복한다.
원소가 하나라면 자기 자신밖에 없으므로 그대로 출력하면 된다.

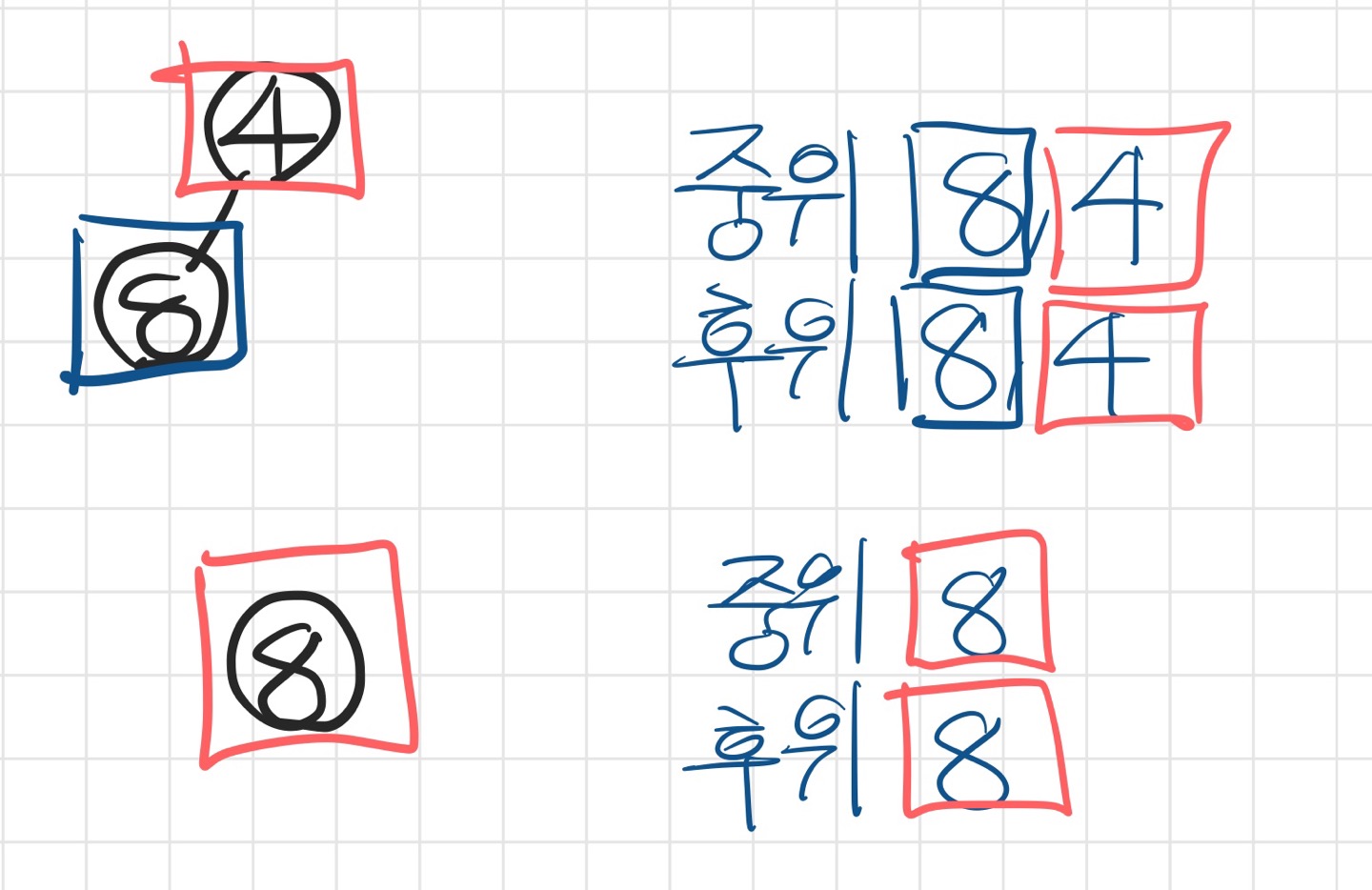
현재 출력 값 : 1 2 4 8

오른쪽 자식 찾기

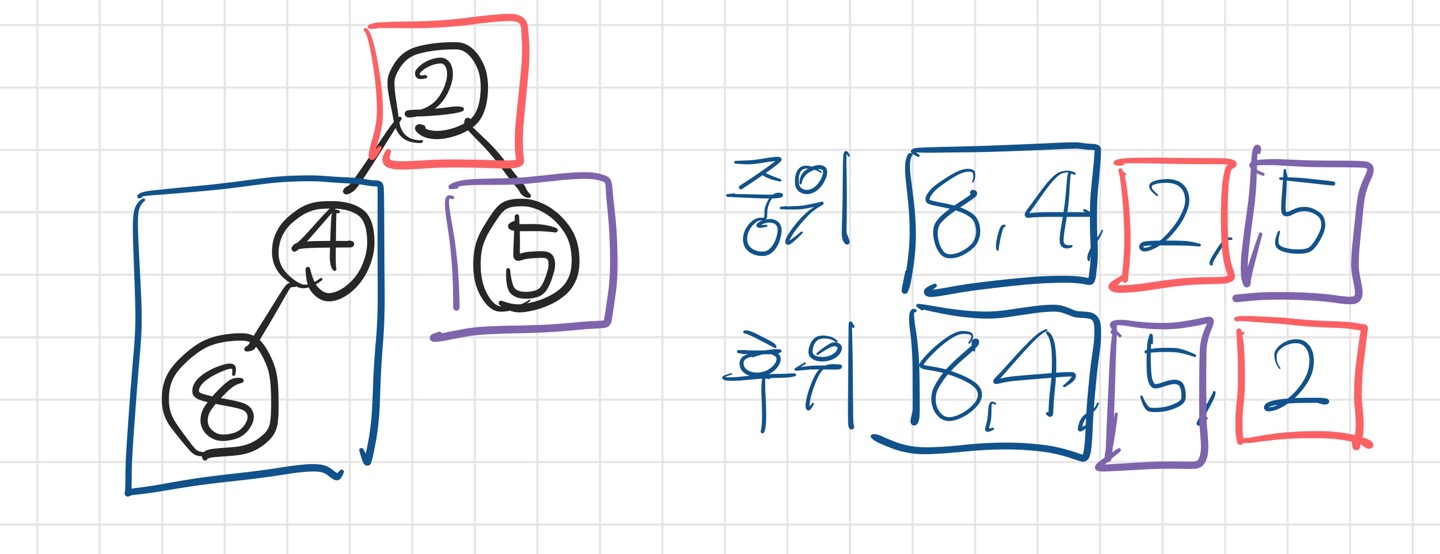
중위 순회는 루트 노드가 가운데, 후위 순회는 루트 노드가 오른쪽 가장 끝에 있으므로 오른쪽 자식의 리스트는 다음과 같이 찾을 수 있다.

(파이썬 리스트 슬라이싱 문법)
중위 순회의 오른쪽 자식 : tree[root_idx+1 :]
후위 순회의 오른쪽 자식 : tree[root_idx : last_idx]

이제 트리를 매개변수로 받는 재귀 함수를 이용하면 된다.
1. 루트노드 출력
2. 왼쪽 자식을 인자로 재귀 함수 호출
3. 오른쪽 자식을 인자로 재귀 함수 호출

이를 통해 출력 결과를 구하면 다음과 같다.

출력 값 : 1 2 4 8 5 3 6 7 9 10

구현

인덱스 전달하기

재귀함수를 호출할 때 리스트를 통째로 복사해서 넘기는 것도 좋은 방법이지만, 문제는 이러면 리스트가 계속 복사되기 때문에 메모리를 많이 사용하게 된다.

때문에 다소 귀찮더라도 왼쪽 자식 트리의 시작 인덱스와 끝 인덱스, 오른쪽 자식 트리의 시작 인덱스와 끝 인덱스를 매개 변수로 넘겨주는 방법을 쓰면 메모리 사용을 줄일 수 있다.

중위 순회 리스트에서 루트노드 인덱스 찾기

파이썬에는 .index() 라는 훌륭한 메서드가 있지만 문제는 이 메서드의 시간 복잡도는 O(N)이다.

즉, 매 재귀마다 .index() 메서드를 사용하여 루트 노드의 인덱스를 찾으면 시간초과가 발생한다.

다행히 이번 경우 리스트에 있는 수는 모두 서로 다른 수이므로, 딕셔너리를 이용해 어떤수가 리스트의 몇번 인덱스에 있는지 저장하면 O(1)의 시간복잡도로 루트 노드의 인덱스를 찾을 수 있다.

in_order_idx = {val: idx for idx, val in enumerate(in_order)}

맵핑 예시
중위 순회 리스트 : [8, 4, 2, 5, 1, 6, 3, 9, 7, 10]
인덱스 맵핑 딕셔너리 : {8: 0, 4: 1, 2: 2, 5: 3, ..., 10: 9}

코드

위 풀이와 구현 방법을 이용한 최종 코드는 다음과 같다.

import sys

sys.setrecursionlimit(10**6)

input = sys.stdin.readline

# 트리
def find_child(in_left, in_right, post_left, post_right):
    if in_left > in_right:
        return
    
    # 프리오더 이므로 루트 바로 출력
    root = post_order[post_right]
    print(root, end=" ")
    
    # 인오더에서 루트의 인덱스 구하기
    root_index = in_order_index[root]
    offset = root_index - in_left
    
    # 왼쪽 자식 탐색
    find_child(in_left, root_index-1, post_left, post_left+offset-1)
    # 오른쪽 자식 탐색
    find_child(root_index+1, in_right, post_left+offset, post_right-1)

N = int(input()) #노드의 개수
in_order = list(map(int, input().split()))
post_order = list(map(int, input().split()))
# 향후 루트 인덱스를 찾게되므로 미리 맵핑해둠
in_order_index = {value: index for index, value in enumerate(in_order)}

find_child(0, N-1, 0, N-1)