[백준] 6549. 히스토그램에서 가장 큰 직사각형 (파이썬)

cjkangme·2023년 7월 9일

알고리즘 파이썬

Algorithm

목록 보기

27/35

문제 : https://www.acmicpc.net/problem/6549

참고자료 (더 설명이 잘 되어있는 글들)
[백준] 6549번 : 히스토그램에서 가장 큰 직사각형 - JAVA [자바]
[BAEKJOON] 6549 히스토그램에서 가장 큰 직사각형

문제 요약

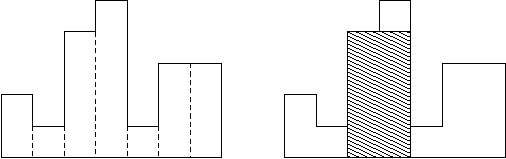
심플하다.
위와 같이 히스토그램이 주어졌을 때, 히스토 그램 내부에서 그릴 수 있는 가장 큰 직사각형을 찾으면 된다.

풀이

분할과 정복

예제로 주어진 히스토그램 기준 분할과 정복으로 mid 기준 왼쪽의 히스토그램을 다음과 같이 탐색할 수 있다.

그리다가 순서가 꼬여서 뒤죽박죽이 되었지만 (아마) 모든 경우의 수를 그렸을 것이다.

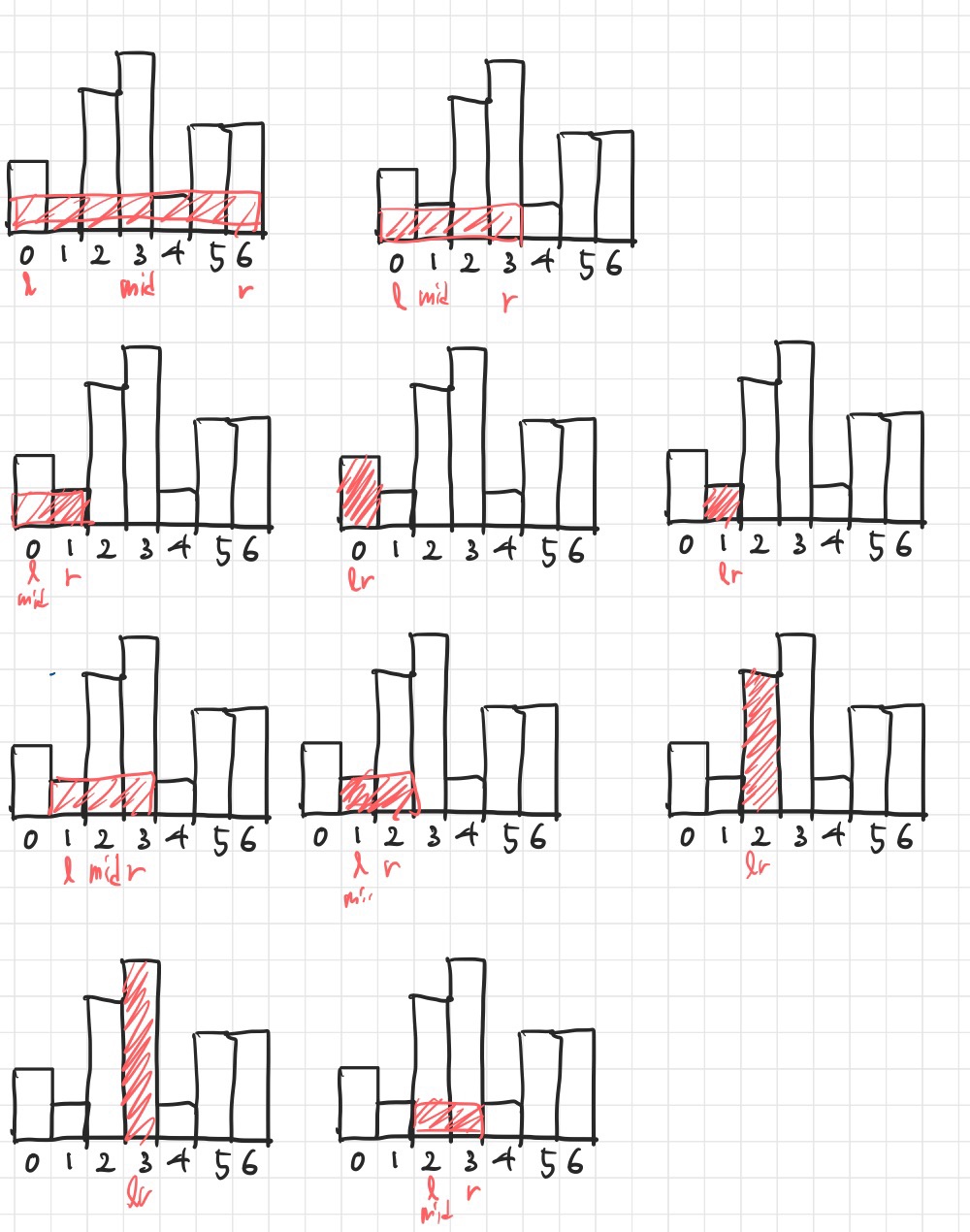
0 ~ 6부터 시작해 mid 3 -> 1 까지 수행했을 때의 탐색할 수 있는 직사각형이다.

그런데 잘 보면 빠져있는 사각형이 있다.

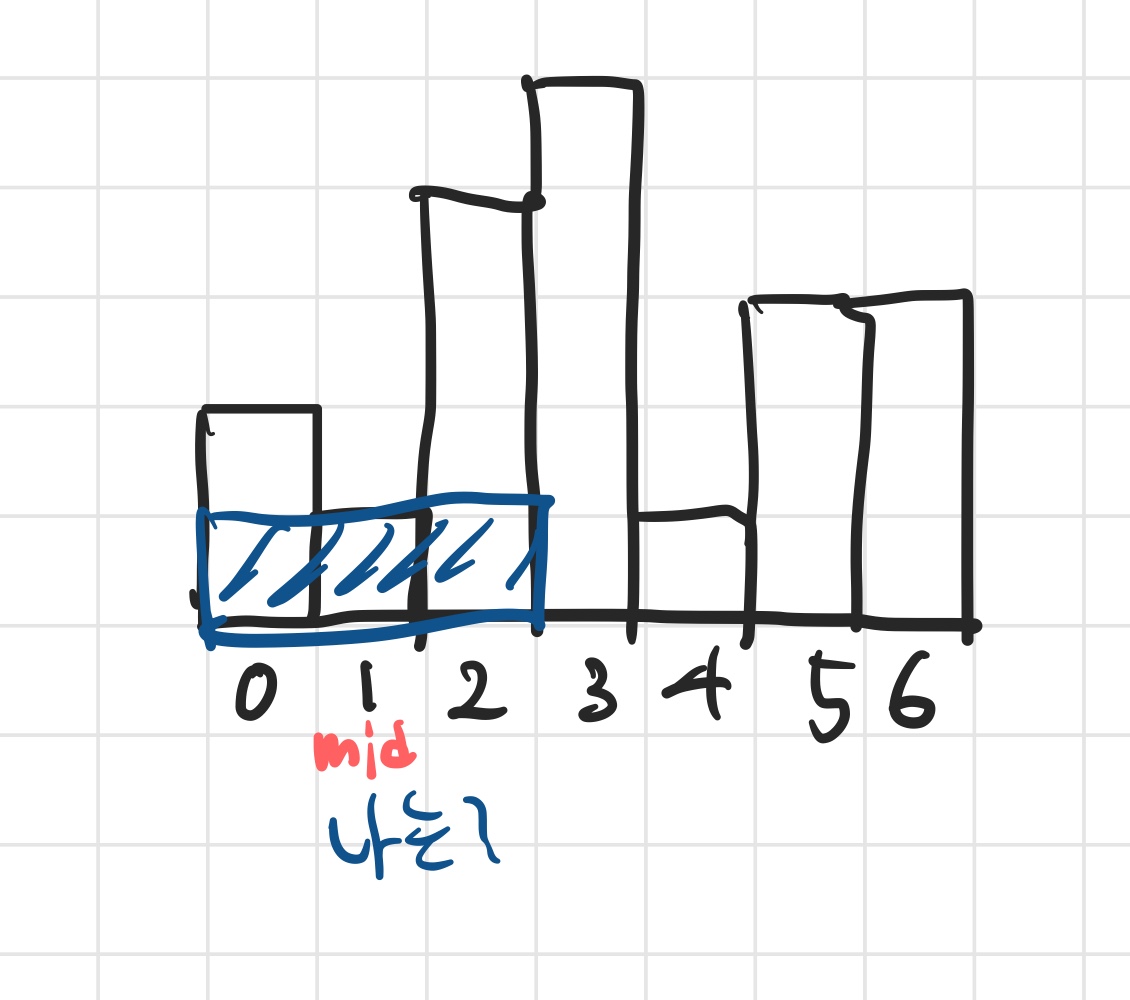
바로 두번째 기준점(mid)이었던 1을 횡단하는 사각형이다.

경우의 수를 따지진 않았지만 첫번째 기준점 3을 횡단하는 아래와 같은 사각형의 넓이 역시 고려하지 못할 것이다.

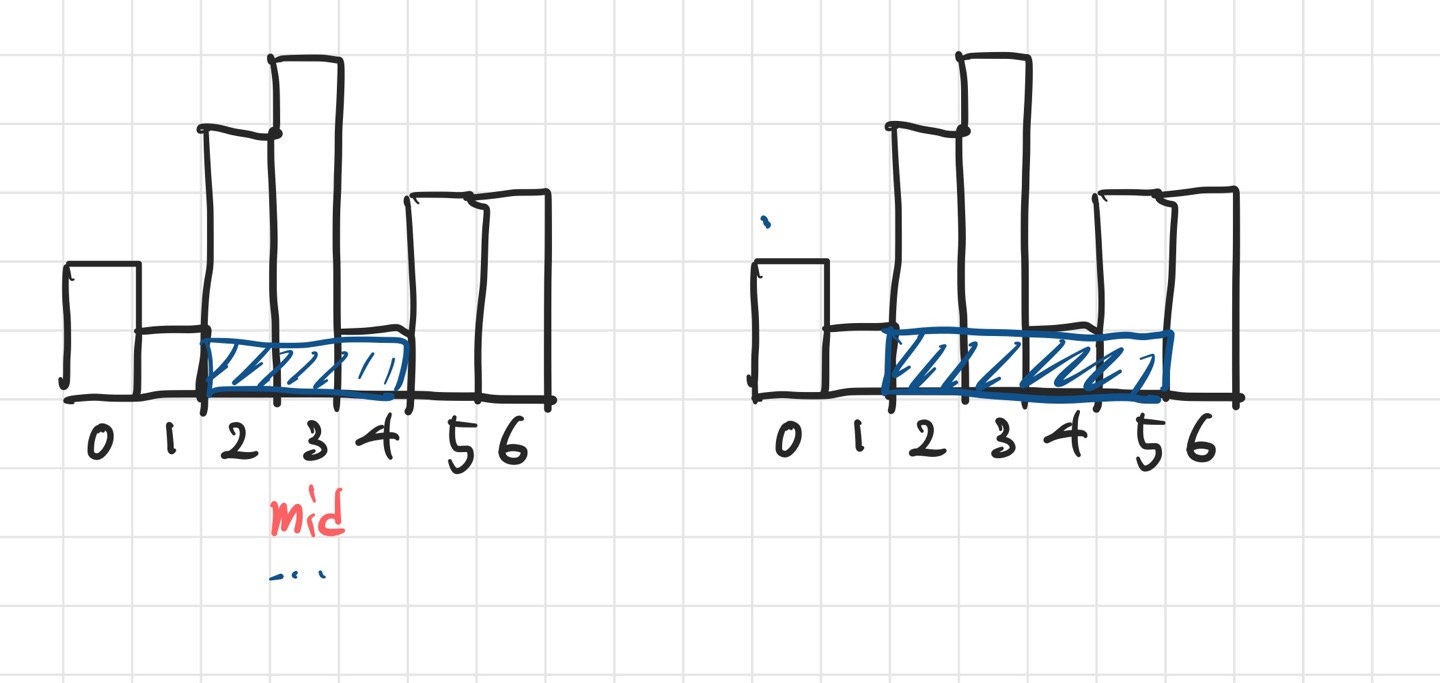
mid부터 출발해서 최대 넓이 구하기

때문에 분할과 정복이 고려하지 못하는 mid 지점부터 좌우로 탐색하면서 최대 넓이를 구해야한다.

뻗어나가는 경우의 수는 왼쪽과 오른쪽 2가지인데, 최대 넓이를 구해야하므로 왼쪽과 오른쪽 중 히스토그램의 넓이가 높은 곳으로 뻗어나가면 된다.

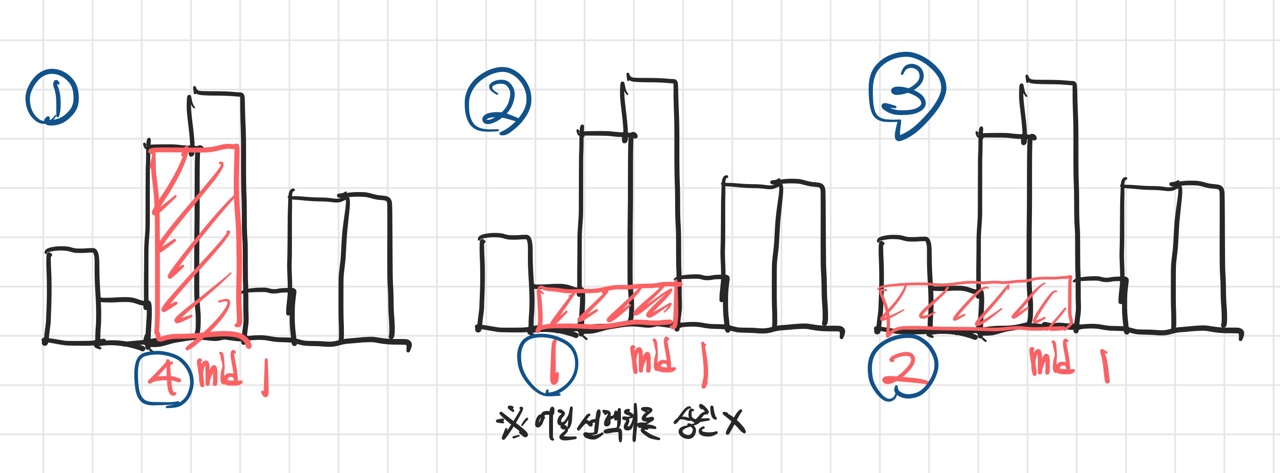
mid를 중심으로 왼쪽과 오른쪽을 비교 -> 왼쪽의 높이가 높으니 왼쪽으로 넓혀서 넓이 구함 (left -= 1)
left와 right가 동일한데 여기서는 왼쪽으로 이동하게 처리했다고 가정 (left -= 1)
left의 높이가 right보다 높으므로 왼쪽으로 넓혀서 넓이 구함 (left -= 1)
left가 탐색 범위를 벗어났으므로 무조건 right쪽으로 확장하며 탐색범위를 벗어날 때까지 탐색 (그림에서는 생략)

이렇게하면 모든 경우의 수를 시간복잡도 O(NlogN)으로 고려하여 답을 구할 수 있다.

코드

※ 사실 저도 제대로 이해 못한 상태로 푼거라 주석을 따로 못달았습니다.

import sys

input = sys.stdin.readline

def devide(left, right):
    global hist
    if left == right:
        return hist[left]
    
    mid = (left + right) // 2
    lmid, rmid = mid, mid+1
    area = max(devide(left, lmid), devide(rmid, right))
    
    height = min(hist[lmid], hist[rmid])
    area = max(area, height * 2, hist[lmid], hist[rmid])
    while (left < lmid or rmid < right):
        if (rmid < right and (lmid <= left or (hist[lmid-1] < hist[rmid+1]))):
            rmid += 1
            height = min(height, hist[rmid])
        else:
            lmid -= 1
            height = min(height, hist[lmid])
        area = max(area, height * (rmid-lmid+1))
    return area
    
while True:
    inputs = list(map(int, input().split()))
    if inputs == [0]:
        break
    answer = 0
    n = inputs[0]
    hist = inputs[1:]
    
    print(devide(0, n-1))