Sample Space
If output is resulted by randomly, it can become a set of outcome.
통계적 실험에서 발생 가능한 모든 집합
S(set)
Event(A) A⊂S
P(A) = Prob(outcome ∈ A)
P(A)는 outcome이 A라는 집합에 속할 확률
Conditional Probability
P(B|A) = P(B∩A) / P(A) = P(B∩A|S) / P(A|S)
The A, B is a subset of Sample Space S.
( A, B 는 Sample Space에 있다고 가정하고 생략)
P(A|B) != P(B|A)
이해하기 쉽게 예를 들어보면, 사건 A가 일어났을 때 B가 발생할 확률과 사건 B가 일어났을 때 A가 발생할 확률은 서로 다르다.
Total Probability
S라는 Sample Space 내에 {A1, A2, A3, A4, ... , An} 으로 구성되어 있다고 가정하자
P(A) = P(A1∩A) + P(A2∩A) + ... + P(An∩A)
조건부 확률의 곱에 의하여 다음과 같이 나타 낼 수 있다.
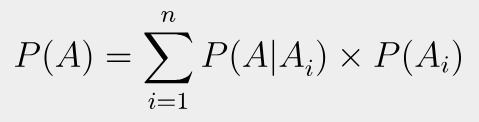
즉 Sample Space 내의 A를 구할 때 A를 다른 배반 사건들의 교집합의 합으로 나타낼 수 있다.
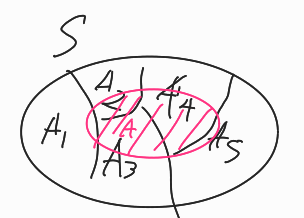
여기서 배반사건이란 A, B가 서로 공통 분모가 없는 상태를 말한다.
즉 P(A∩B)=0 이다.
독립사건은 두 사건 A, B가 서로 일어날 확률에 영향을 미치지 않는 상태를 말한다.
즉 P(A) * P(B) = P(A∩B) 를 말한다.
Bayesian Theorem
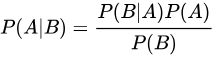
위 식과 같이 P(A|B)를 조건부 확률이 아닌 식으로 정의 할 수 있는데 이를 Bayesian Theorem 이라 한다.
위 식에서 P(B|A)는 조건부 확률에 의해 아래와 같이 정의 되는데, 대입해보면 참이 된다.
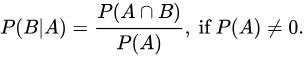
따라서 우리는 P(A|B)에 대한 정보가 없어도 P(B|A)라는 Priori(사전지식)을 알고 있으면 쉽게 구할 수 있다