Image Operations

한 장 이상의 영상으로 새로운 영상을 생성할 때 사용하는 연산과정이다.

Arithmetic Operations

4가지 연산

$s(x,y)=f(x,y)+g(x,y)$
$d(x,y)=f(x,y)-g(x,y)$
$p(x,y)=f(x,y)\times g(x,y)$
$v(x,y)=f(x,y)\div g(x,y)$

어디에 사용될까?

• Noise Processing
• Intensity manipulation
• Background/foreground subtraction
• Region Masking

예시

noise를 줄이기 위한 픽셀 평균 구하기

첫 번째 영상을 보면 noise가 굉장히 심한 것을 알 수 있다. 민감도를 높게 설정하여 어두운 배경에서도 밝게 나왔다. 이 민감도를 낮추면서 영상을 생성하고 그 값들의 평균을 사용하면 noise가 줄어듦을 알 수 있다. 순차적으로 5장, 10장, 20장, 50장, 100장의 영상을 연산한 것이다.

영상은 보통

$\mu+\epsilon$
$\epsilon \sim N(0,\gamma)$

다음과 같은 특징을 갖기 때문에 여러장을 사용할수록 본래의 값 $\mu$에 가까워짐을 확인할 수 있다.

값의 차를 이용한 영상 추출

뇌 주변의 혈관에 대해 관찰하고 싶을 때

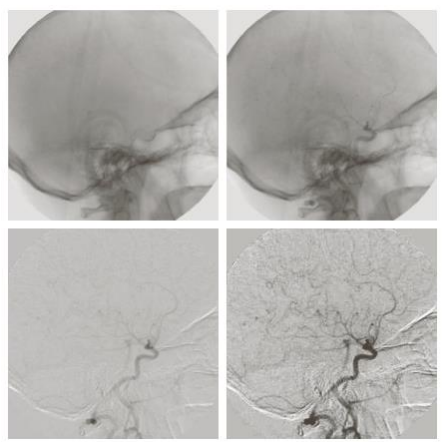
조영제를 넣기 전과 후의 영상의 intensity 차를 이용하고 앞선 포스터에서 배운 Intensity 변화를 한번 더 사용하면 마지막 그림처럼 혈관에 대해 자세히 볼 수 있다.
어떤 Intensity변화를 사용한건지 모르겠지만 로그함수를 이용하면 될 것 같다. 감마 함수를 이용하여 더 잘 보이게 만들 수도 있어 보인다.

Shading correction

첫번째 영상은 현미경으로 찍을 텅스텐 필라멘트인데 영상의 왼쪽 위가 오른쪽 아래에 비해 밝다. 이를 보정하기 위해 Shading pattern을 원본 영상과 연산하여 3번째처럼 shading을 없애줄 수 있다.

논리 연산

우리가 흔히 알고 있는 논리 연산을 이용한 영상처리 기법이다.

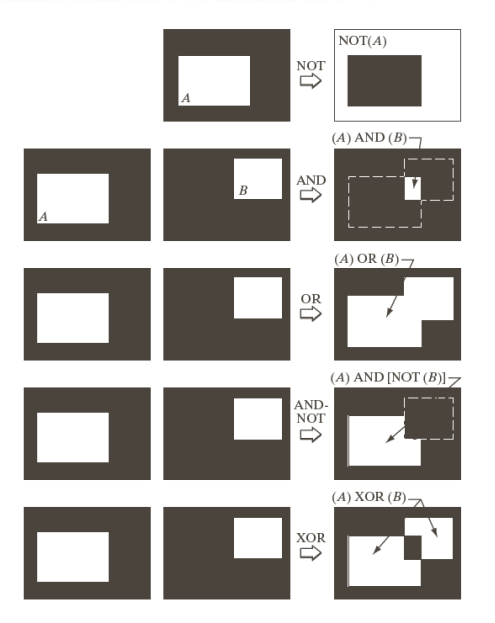
Spatial Operations

지금까지 한 픽셀에 대해 변환했던 것과 달리 주변 픽셀값을 고려해 한 픽셀의 값을 계산하는 것이다. Neighborhood Operation이라고 한다. 아래 Geometric Transformation에서 활용될 예정이다.

Gemometric Transformation

이 변환은 픽셀의 intensity는 건들지 않고 픽셀 좌표값을 변환하는 것이다.

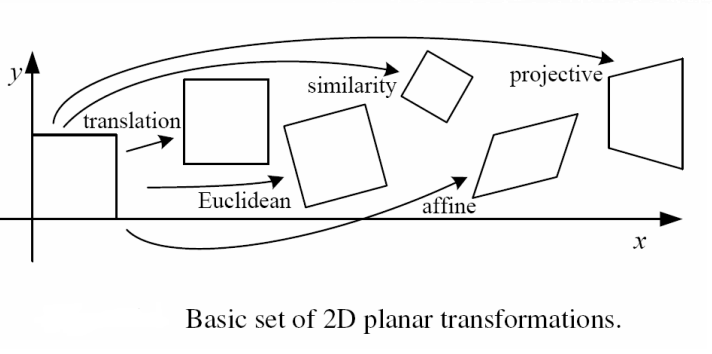
• translation: 이동
• Euclidean: 이동 + 회전
• similarity: 이동 + 회전 + 크기변화
• affine: 원본의 비율 변화, 찌그러졌지만 평행 유지
• projective: 원근법처럼 특정 시점에서 보이는 모습처럼 생김

눈으로만 살펴보면 위와 같이 정리할 수 있겠다.

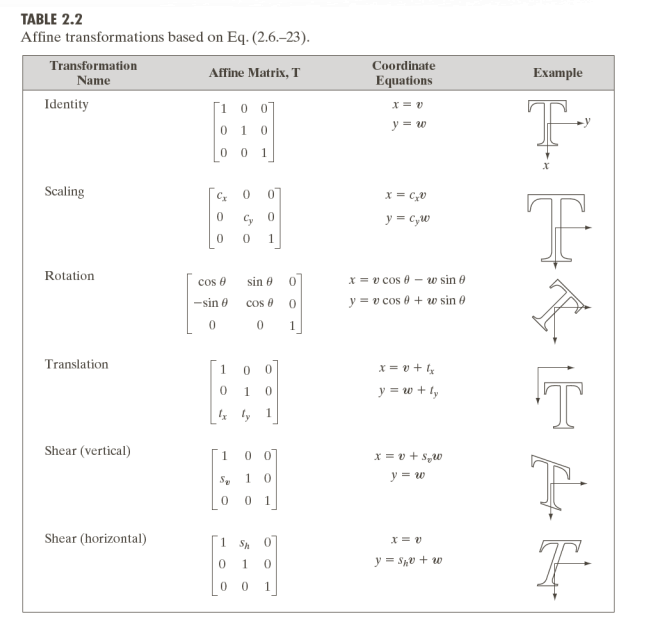
2D 변환

결론부터 말하면 projective를 제외한 2차원 변환은 아래 a,b,c,d,e,f 값을 조절하여 바꿀 수 있다.

$\begin{bmatrix}F\\G\\ \end{bmatrix}$=$\begin{bmatrix}a&b\\d&e\\ \end{bmatrix}$$\begin{bmatrix}x\\y\\ \end{bmatrix}$+$\begin{bmatrix}c\\f\\ \end{bmatrix}$

translation

$\begin{bmatrix}F\\G\\ \end{bmatrix}$=$\begin{bmatrix}1&0\\0&1\\ \end{bmatrix}$$\begin{bmatrix}x\\y\\ \end{bmatrix}$+$\begin{bmatrix}c\\f\\ \end{bmatrix}$

scaling

$\begin{bmatrix}F\\G\\ \end{bmatrix}$=$\begin{bmatrix}a&0\\0&e\\ \end{bmatrix}$$\begin{bmatrix}x\\y\\ \end{bmatrix}$+$\begin{bmatrix}0\\0\\ \end{bmatrix}$

rotation

$\begin{bmatrix}F\\G\\ \end{bmatrix}$=$\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\\ \end{bmatrix}$$\begin{bmatrix}x\\y\\ \end{bmatrix}$+$\begin{bmatrix}0\\0\\ \end{bmatrix}$

shear

$\begin{bmatrix}F\\G\\ \end{bmatrix}$=$\begin{bmatrix}1&b\\d&1\\ \end{bmatrix}$$\begin{bmatrix}x\\y\\ \end{bmatrix}$+$\begin{bmatrix}0\\0\\ \end{bmatrix}$

rigid (translation & rotation)

$\begin{bmatrix}F\\G\\ \end{bmatrix}$=$\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\\ \end{bmatrix}$$\begin{bmatrix}x\\y\\ \end{bmatrix}$+$\begin{bmatrix}c\\f\\ \end{bmatrix}$

길이와 각도는 보존된다.

affine

$\begin{bmatrix}F\\G\\ \end{bmatrix}$=$\begin{bmatrix}a&b\\d&e\\ \end{bmatrix}$$\begin{bmatrix}x\\y\\ \end{bmatrix}$+$\begin{bmatrix}c\\f\\ \end{bmatrix}$

평행만 보존된다.

Image registration

두 장 이상의 영상을 겹치고 싶을 때 사용.
예를 들어, 파노라마 영상을 촬영한다고 생각하자. 좌측에서 한번 우측으로 가서 한번 찍었을 때 두 영상의 교집합 부분을 정확히 매칭해야 한다. 매칭할 때 사람이 찍었으므로 교집합 부분의 각도, 길이가 다를 수 있다. 그럼 둘 중 하나의 영상을 affine변환으로 각도와 크기를 맞출 필요가 있다. 어떻게 하면 될까?

affine변환을 보면 우리가 알아야 할 변수 a,b,c,d,e,f 총 6개가 있다. 그럼 교집합에서 일치하는 픽셀의 좌표를 비교해보면 된다. 알아야할 변수는 6개이므로 왼쪽의 영상에서 3개 그리고 거기에 대응하는 오른쪽 영상에서 3개의 좌표를 계산할 수 있다. 혹은 여러개의 좌표를 통해 오차를 줄이는 방식을 사용할 수도 있다.

근데 대응하는 좌표를 어떻게 찾나 ? 앞에서 살펴본 neighborhood 특징을 활용해 좌표 대 좌표로 비교하는 것이 아닌 작은 영역끼리 비교하는 것이다.

Homogeneous Coordinates

만약 100x100, 즉 10000개의 픽셀값을 가진 영상을 계속 좌표변환한다고 생각해보자. 좌표 변환 한번에 10000번 이상의 연산을 해야 한다. 굉장히 비효율적이다.
그럼 변환 계산식들을 먼저 계산한다면 어떨까?
그래도 x,y에 붙은 계수들만 있으면 모를까 뒤에 $\begin{bmatrix}c\\f\\ \end{bmatrix}$처럼 더하는 값도 있어서 계산이 상당히 복잡할거라 생각한다.
그래서 사용하는 것이 Homogeneous Coordinate다.

$\begin{bmatrix}F\\G\\ \end{bmatrix}$=$\begin{bmatrix}a&b\\d&e\\ \end{bmatrix}$$\begin{bmatrix}x\\y\\ \end{bmatrix}$+$\begin{bmatrix}c\\f\\ \end{bmatrix}$

homogeneous coordinate에서는

$\begin{bmatrix}F\\G\\I \end{bmatrix}$=$\begin{bmatrix}a&b&c\\d&e&f\\0&0&1 \end{bmatrix}$$\begin{bmatrix}x\\y\\1 \end{bmatrix}$

이제 이렇게 homogeneous coordinate에서는 변환식들을 합성하기 수월할 것이다.

또한 계산량을 줄여준다는 장점 외에도 영상 왜곡을 감소시켜주는 효과가 있다. 무슨 말이냐?
rotate변환을 할 때 픽셀들이 정확히 다음 좌표의 픽셀의 정가운데에 위치할 확률이 매우 적다. 그렇다보니 픽셀의 값이 회전을 거듭할수록 변하거나 소실될 수밖에 없다. 따라서 homogeneous coordinate를 이용한 변환 합성을 먼저 해주는 것이 영상 왜곡을 조금 막아준다.

그리고 컴퓨터 그래픽스 수업에서 배운 내용은 rotate 변환식은 원점을 기준으로 한 회전이다. 따라서 이동을 하고 회전하는 것과 원점에서 회전하는 것을 다른 결과를 만든다. 따라서 이 점을 고려하면 homogeneous coordinate를 사용하는 것이 안전해 보인다.

Interpolation

우리가 영상을 확대하면 어떻게 될까? 원본 영상의 픽셀값은 굵직하게 있는데 픽셀은 더 세세하게 표현해야 한다. 없는 정보를 가지고 어떻게 표현해야하나? 그냥 검은색으로 나타낸다면 영상이 전체적으로 어두워질 것이다. 따라서 다음 3가지 방법이 있다.

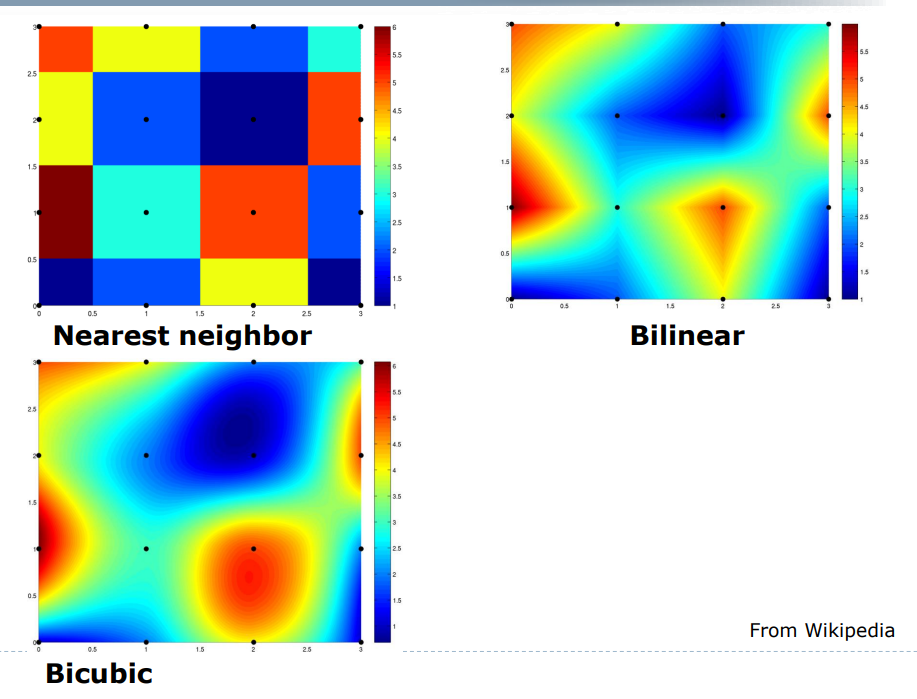
• Nearest neighbor
  맨하탄 거리를 통해 가장 가까운 픽셀의 값을 그대로 사용한다.
• Bilinear interpolation
  4개의 점에서 거리에 대한 비율을 토대로 색을 정한다.
• Bicubic interpolation
  16개의 점을 이용해 색을 정한다.
  

정리

가벼운 행렬 연산으로 시작해서 geometric 변환 그리고 interpolation에 대해 알아보았다. 파노라마 사진의 원리가 좌표 변환을 이용한 사실은 처음 알게됐고 굉장히 재미있었다. 영상 처리에 대한 다양한 개념을 내 것으로 만들고 활용하고 싶은 욕구가 생겼다.