🖐 본 글은 Red-Black Tree를 구현하는 방법에 대한 설명글이 아니다. Red-Black Tree의 구현자가 아닌 사용자의 관점에서 반드시 알고 넘어가야 하는 특성들에 대해 담아봤다. 구현은 다음을 참고

0. 일반적인 Binary Search Tree에 비해 Red-black Tree가 가지는 강점

기본적으로 Red-black Tree(rb tree)는 binary serach tree(bst)이다. rb tree는 bst에서 제공하는 대부분의 operation(예: search)들에 대해 시간 복잡도가 최악의 경우에도 O(*n)이 아닌 O(logn)을 유지할 수 있다. bst에서 operation들의 시간복잡도는 bst의 높이인 h에 달렸는데, 최악의 경우 h=n이다. 반면 rb tree에서는 self-balancing 메카니즘 덕분에 높이인 h가 <=2log2(n+1)으로 유지되기 때문이다.

*n은 트리의 모든 노드의 수이다

1. Red-black Tree의 높이(h)가 아무리 커도 2log2(n+1)을 넘을 수 없는 이유

네 줄 요약

• (1) n >= 2^k-1
• (2) k <= log2(n+1), 왜냐하면 (1)에 log2 적용
• (3) 경로 위 black node 수 <= log2(n+1), 왜냐하면 property 5 및 (2)
• (4) h <= 2log2(n+1), 왜냐하면 property 3 및 (3)

자세한 내용
1. 어떤 binary tree가 있다고 했을 때, k를 root에서 leaf로 가는 모든 경로들에 대해서 각각의 경로 위에 존재해야 하는 최소 노드수라고 정의하자. 참고로 root와 leaf 포함이며, rb tree에서 leaf는 nil 노드이다. 다음으로 tree의 모든 노드의 수를 n이라고 하면, n >= 2^k-1이다. 2^k-1이 어떻게 나왔는지 이해가 안 된다면, perfect binary tree의 특성을 참조하라. 아무튼 이 부등식을 다르게 표현하면 k <= log2(n+1)이 된다. 다시 k와 n의 정의와 연결지어 생각하면, 총 노드의 수가 n인 binary tree의 root에서 leaf로 가는 모든 경로들에 대해서 각각의 경로 위에 존재하는 최소 노드수는 log2(n+1)을 초과할 수 없다. 예를 들어, n=3인 binary search tree가 있다고 하자. 위의 정리에 따르면 k는 2(=log2(3+1))을 넘길 수 없다. 만약 k가 3이라면 n은 최소 7이 되어버리기 때문에 불가능하다.
1. rb tree의 다섯 번째 property에 따라, 모든 노드(root 포함)들은 자신과 자신의 leaf로 이어지는 모든 경로에 존재하는 black node의 수(black height)가 같아야 한다. 이 특성과 더불어 위에서 정리한 내용으로 인해 root에서 leaf로 가는 모든 경로들에 대해서 각각의 경로 위에 존재하는 모든 black node의 수는 최대 log2(n+1)을 넘길 수 없다.
1. rb tree의 네 번째 property에 따르면 모든 red node는 또 다른 red node와 인접할 수 없다. 또한 세 번째 property에 따르면 모든 leaf node는 검정색이다. 이 두 가지 property에 따르면 rb tree에서 높이가 되는 경로에 있는 node들 중 black node가 최소 절반 이상을 차지한다. 이 특성과 바로 앞에서 정리한 내용을 합치면, rb tree의 높이는 2log2(n+1)을 넘길 수 없게 된다. h <= 2log2(n+1). 이 부분이 나도 바로 이해되지는 않았다. 천천히 다시 생각해보자. 앞에서 root에서 leaf로 가는 모든 경로들에 대해서 각각의 경로 위에 존재하는 모든 black node의 수는 log2(n+1)을 넘길 수 없다라고 정리했다. root에서 leaf로 가는 경로가 있다고 했을 때, 그 경로 상에 존재하는 black node의 개수는 log2(n+1)을 넘길 수 없다고 한 것이다. 각 경로에는 black node 혹은 red node가 존재할 수 있고, 그 외의 색을 가진 node는 존재할 수 없다. black node의 수의 upper bound는 확인했으니, red node의 수만 세어주면 된다. 그런데 red node는 또 다른 red node와 인접할 수 없다고 했고 leaf node는 검정색이기 때문에, red node의 수는 black node의 수를 초과해서 존재할 수 없다. 따라서 root에서 leaf로 가는 경로 상에는 최대 log2(n+1) + log2(n+1)개의 노드보다 많은 노드가 존재하는 것이 불가능한 것이다. 다시 정리하면 h <= 2log2(n+1)가 성립한다.

2. insertion, deletion의 시간 복잡도가 log(n)인 이유

• Insertion의 시간 복잡도가 O(logn)인 이유

  • 삽입할 위치를 찾아 최초 삽입하는 데 logn 시간 복잡도
  • fixup을 할 때 case 1이 계속 포인터의 위치를 grand_parent로 옮기면서 최악의 경우 logn, case 2에 걸리면 case 3로 가면서 loop가 종료되므로 상수 시간 복잡도
  • 결론적으로 logn + logn => O(logn)
  • 참고로 최악 2번의 rotation(case 2 -> case 3)

• Deletion의 시간 복잡도가 log(n)인 이유

  • 삭제할 노드를 찾는 데 logn 시간 복잡도
  • 조건에 따라 다양한 로직으로 supplant하고 부모 자식 관계들 정리하는 데 상수 복잡도
  • fixup을 하는 데 logn 시간 복잡도(case 2가 계속 반복되는 경우가 최악)
    • case 1에 걸리면 한 번의 rotation 후 case 2, case 3, case 4로 이동
    • case 2에 걸리면 rotation 없이 case 1, case 2, case 3, case 4로 이동. 참고로 case 1에서 case 2로 넘어왔다면 case 2에서 loop가 종료됨
    • case 3에 걸리면 한 번의 rotation 후 case 4로 넘어감
    • case 4에 걸리면 한 번의 rotation 후 loop가 종료됨
  • 결론적으로 logn + 상수 + logn => O(logn)
  • 참고로 최악 3번의 rotation(case 1 -> case 3 -> case 4)

3. rb tree를 공부하면서 오해해서 시간 날리기 쉬운 부분들

3.1 Deletion 부분에서의 오해

• 보조 그림의 f, g, h, i, l, k가 nil nodes라고 오해
  codesdope 사이트(figures below are from codesdope) 설명에서 다음 그림의 case 1을 보면서, '왜 B까지의 black nodes는 root 포함 3개이고, D나 E까지의 black nodes는 2개인데 property 5가 깨지지 않는다고 하는거지?'와 같은 의문 때문에 힘들었다. case 3과 case 4에서도 마찬가지였다. 결국 Introduction to algorithms 책을 보면서 오해가 해결됐다. 아래 사진에서 f, g, h, i, l, k 등은 nil nodes가 아니라 subtree를 축약해서 보여준 것이였다.
  

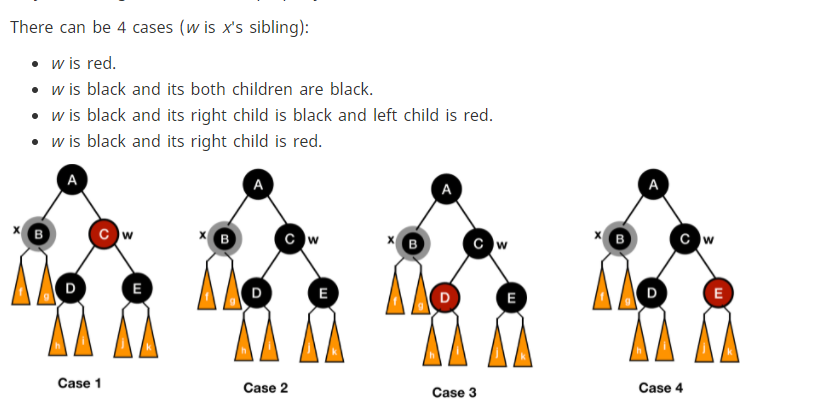
• Case 1에서 변환 후 black height가 깨지지 않는 이유
  B에서의 black height와 D에서의 black height, E에서의 black height가 같은 상태로 시작. 이걸 생각하고 case 1이 transform 완성된 사진을 보면 property 5가 깨지지 않는 것을 알 수 있다.
  

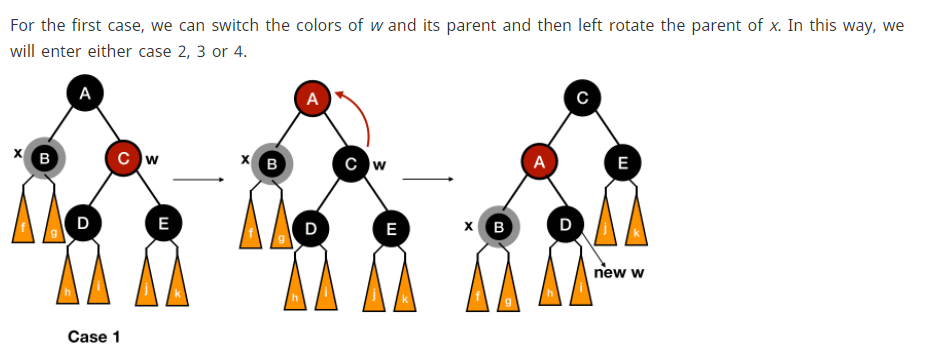
• Case 2에서 변환 후 black height가 깨지지 않는 이유
  이건 당연하다. B랑 C에서 Black node를 하나씩 빼줬기 때문에 black height property는 문제가 없다.
  

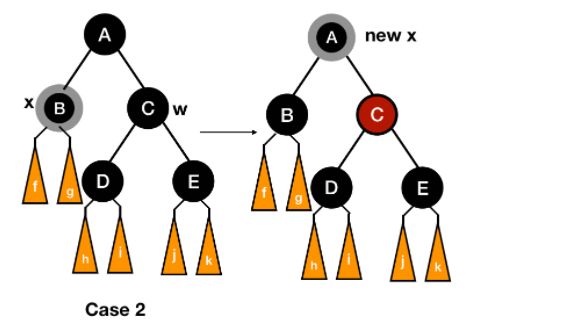
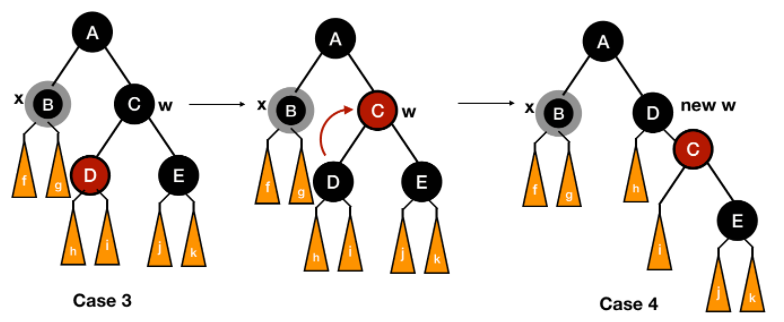
• Case 3랑 Case 4에서 balck height property가 깨지지 않는 이유
  Case 1이랑 Case 2에서도 적용가능한 방법인데, 모든 노드들에 바꾸기 전 기준 black height를 적어놓고, 실제로 돌려보면 black height property 깨지지 않는 것을 확인 할 수 있다. 예를 들어 아래 그림에서, A에는 height=n, B의 height=n-1, C의 height=n-1, D의 height=n-2, E의 height=n-1 이런 식으로 잡고, 조건이 시키는 대로 변환해보면 여전히 black height property가 지켜지는 것을 확인할 수 있다.
  

4. rb tree 구현 디테일 복습에 도움이 될 자료들

1. Introduction to algorithm 3rd edition: 이 책이 어렵다는 소문으로 멀리하고 있었다. 인터넷에서 각종 웹사이트들 및 유튜브 동영상 강의들 보면서 설명이 부족한 부분들 때문에 고생하다가, 이 책의 자세한 설명을 보고 모든 오해했던 지점들이 말끔히 해소됐다. 무서워하지 말고 반드시 봐야하는 1순위 참고자료. pseudo code가 담겨있지만, 사용하는 프로그래밍 언어에 맞게 조금만 손 보면 바로 구현 코드를 짤 수 있다.
2. codesdope 웹사이트의 red-black tree deletion 설명: Deletion에서 4가지 case들에 대해 도식화된 부분이 이해하기 쉽게 정리되어 있어, Introduction to algorithm의 보조 자료로 시너지가 크다.
3. 내가 작성한 주석이 달린 rb tree c 프로그램: deletion logic에 대해서 특히 자세히 주석을 남겼다.

5. 사소한 디테일

• root의 부모 노드와 nil 노드들을 표현할 오직 한 개의 노드로 Sentinel Node를 사용하면 insertion fixup과 deletion fixup 함수를 구현할 때 boundary check하는 과정이 정말 쉬워진다. 개인적으로 sentinel node를 사용하지 않고 null pointer로 nil 노드들을 표현해서 구현을 시도했으나 너무 지저분해져서 sentinel node를 쓰는 것으로 방향을 바꿨다.