기본적인 정렬 알고리즘 5개

Rosevillage·2023년 3월 3일
TILalgorithm자료구조
0

거품정렬, 선택정렬, 삽입정렬, 병합정렬, 퀵정렬의 특징과 작동 방식에 대해 알아본다.

거품정렬

두개의 숫자를 비교해 더 큰 숫자를 오른쪽으로 보내는 방식의 정렬로,
가장 큰 수를 가장 오른 쪽으로 보내는 것 같이 동작한다.

  • stable 정렬에 해당한다.

  • 시간복잡도

    최악, 최선, 평균 모두 O(n^2)으로 성능이 좋지는 않다. 그러나 구현이 간단하고, 직관적이라는 장점을 지닌다.

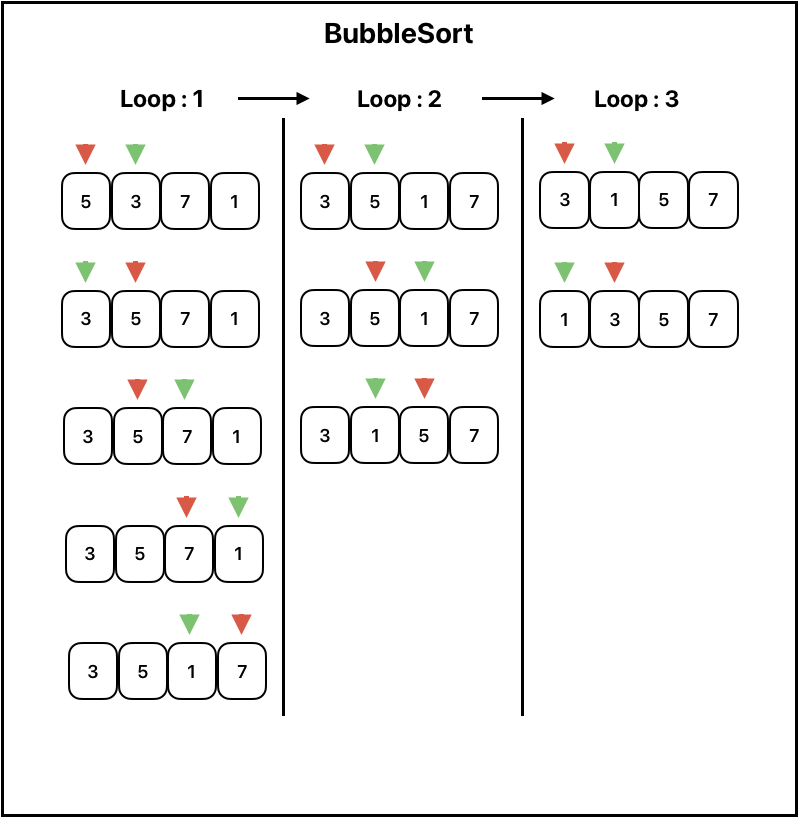
function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
      console.log(`count ${i}:` , arr)
    for (let j = 1; j < arr.length - x; j++) {
      if (arr[j - 1] > arr[j]) {
        [arr[j - 1], arr[j]] = [arr[j], arr[j - 1]];
      }
        console.log('inner:' , arr)
    }
  }
  return arr;
}
let newArr = [5,3,7,1];
console.log(bubbleSort(newArr))

/**
count 0: [ 5, 3, 7, 1 ]
inner: [ 3, 5, 7, 1 ]
inner: [ 3, 5, 7, 1 ]
inner: [ 3, 5, 1, 7 ]
count 1: [ 3, 5, 1, 7 ]
inner: [ 3, 5, 1, 7 ]
inner: [ 3, 1, 5, 7 ]
count 2: [ 3, 1, 5, 7 ]
inner: [ 1, 3, 5, 7 ]
count 3: [ 1, 3, 5, 7 ]
[ 1, 3, 5, 7 ]
**/

선택정렬

가장 작은 숫자를 찾아 특정 숫자와 비교후 위치를 교환하는 방식의 정렬로, 비교 횟수에 비해 교환 횟수가 적다.

많은 교환이 일어나야 하는 자료 상태에서 비교적 효율적이다.

  • 구현 방식에 따라 달라질 수 있지만 대체적으로 unstable 정렬에 해당한다.

  • 시간복잡도

    최악, 최선, 평균 모두 O(n^2)으로 거품정렬과 마찬가지로 성능이 좋지않으면서, 구현이 간단하다.

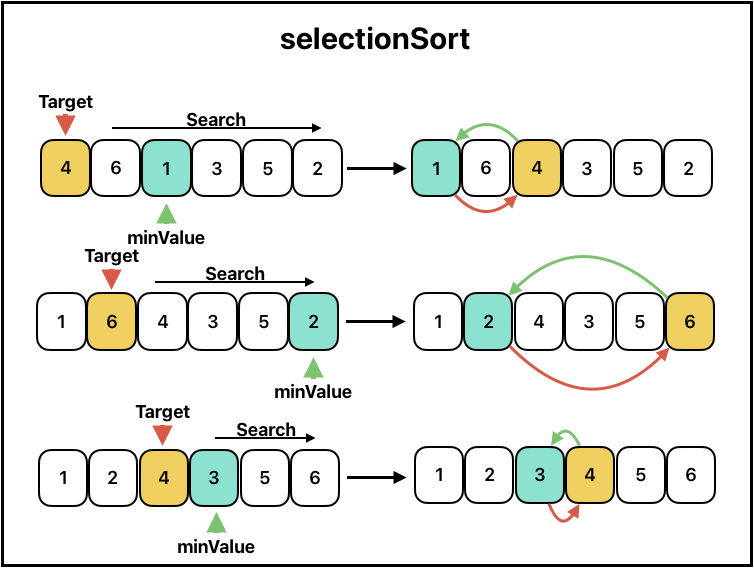
function selectionSort(arr) {
  let minIdx;
  for (let i = 0; i < arr.length - 1; i++) {
    minIdx = i;
    //console.log(`loop: `,i)
    //console.log(`initial min : ${arr[minIdx]}`, arr)
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[minIdx]) {
        minIdx = j;
      }
     // console.log(`inner min : ${arr[minIdx]}`, arr)
    }
    [arr[i], arr[minIdx]] = [arr[minIdx], arr[i]];
    //console.log(`change : ${arr}`)
  }
  return arr;
}
let newArr = [4,6,1,3,5,2];
console.log(selectionSort(newArr))

/**
loop:  0
initial min : 4 [ 4, 6, 1, 3, 5, 2 ]
inner min : 4 [ 4, 6, 1, 3, 5, 2 ]
inner min : 1 [ 4, 6, 1, 3, 5, 2 ]
inner min : 1 [ 4, 6, 1, 3, 5, 2 ]
inner min : 1 [ 4, 6, 1, 3, 5, 2 ]
inner min : 1 [ 4, 6, 1, 3, 5, 2 ]
change : 1,6,4,3,5,2

loop:  1
initial min : 6 [ 1, 6, 4, 3, 5, 2 ]
inner min : 4 [ 1, 6, 4, 3, 5, 2 ]
inner min : 3 [ 1, 6, 4, 3, 5, 2 ]
inner min : 3 [ 1, 6, 4, 3, 5, 2 ]
inner min : 2 [ 1, 6, 4, 3, 5, 2 ]
change : 1,2,4,3,5,6

loop:  2
initial min : 4 [ 1, 2, 4, 3, 5, 6 ]
inner min : 3 [ 1, 2, 4, 3, 5, 6 ]
inner min : 3 [ 1, 2, 4, 3, 5, 6 ]
inner min : 3 [ 1, 2, 4, 3, 5, 6 ]
change : 1,2,3,4,5,6

loop:  3
initial min : 4 [ 1, 2, 3, 4, 5, 6 ]
inner min : 4 [ 1, 2, 3, 4, 5, 6 ]
inner min : 4 [ 1, 2, 3, 4, 5, 6 ]
change : 1,2,3,4,5,6

loop:  4
initial min : 5 [ 1, 2, 3, 4, 5, 6 ]
inner min : 5 [ 1, 2, 3, 4, 5, 6 ]
change : 1,2,3,4,5,6

[ 1, 2, 3, 4, 5, 6 ]
**/

삽입정렬

작은 수가 나올때 까지 숫자들을 오른쪽으로 밀고, 삽입하는 방식의 정렬

버블 정렬의 비교 및 교환 횟수를 줄임으로써 높은 효율을 보여준다.

배열이 길어질수록 효율이 떨어지지만, 입력으로 들어오는 배열의 원소가 정렬되어있을수록 속도가 빠르며, 정렬된 값은 교환이 일어나지 않는다.

  • Stable 정렬에 해당한다.

  • 시간복잡도

    최악, 평균은 O(n^2), 최선은 O(n)이며, 구현이 간단하고 선택 정렬이나 거품 정렬과 같은 O(n^2) 알고리즘에 비해 빠르다.

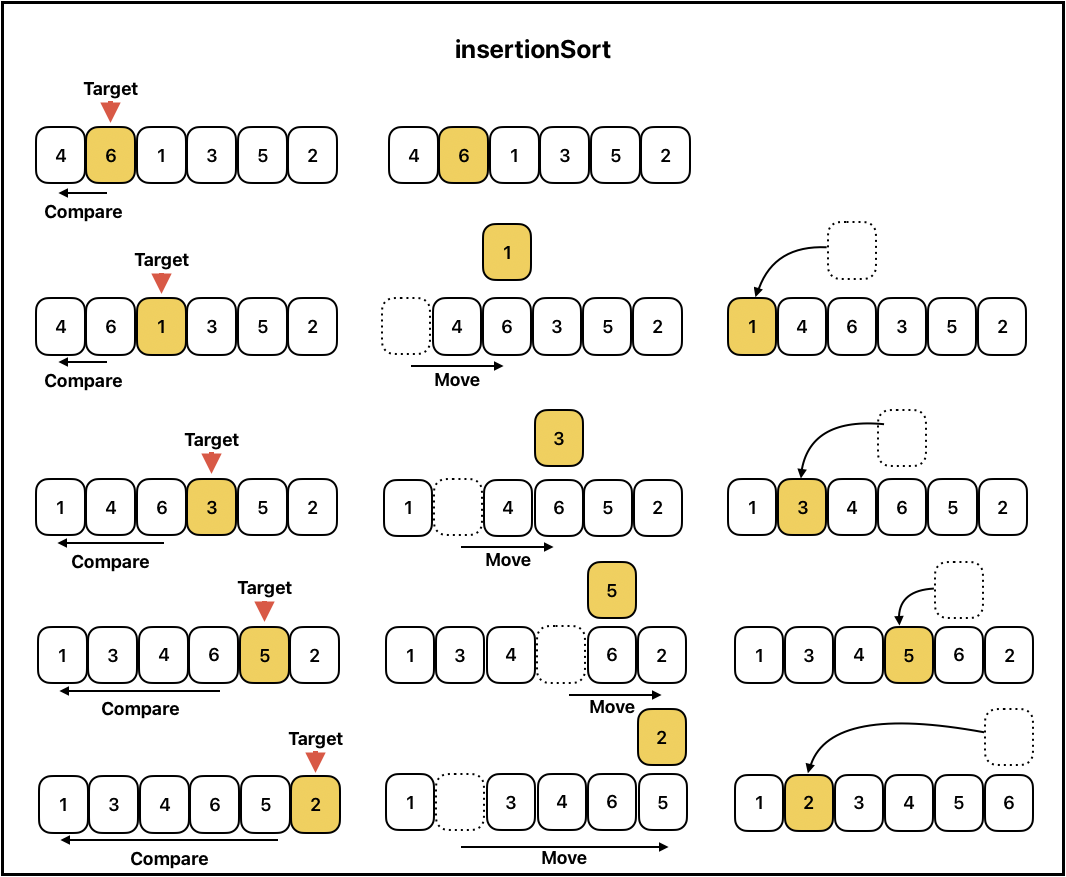
function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let target = arr[i];
    let prev = i - 1;
    //console.log('index='+i,'|','target='+target);
    while (prev >= 0 && arr[prev] > target) {
        //console.log('prev='+prev,'|', 'selectPrev='+arr[prev],'\n', 'before: ',arr)
      arr[prev + 1] = arr[prev];
      prev--;
    //console.log(' after: ',arr)
    }
    arr[prev + 1] = target;
    //console.log('prev='+prev,'\n',i,'loop End:' ,arr+'\n')
  }
  return arr;
}
let newArr = [4,6,1,3,5,2];
console.log(insertionSort(newArr))

/**
i=1 | target=6
prev=0 
 1 loop End: 4,6,1,3,5,2

i=2 | target=1
 prev=1 | selectPrev=6 
  before:  [ 4, 6, 1, 3, 5, 2 ]
  after:  [ 4, 6, 6, 3, 5, 2 ]

 prev=0 | selectPrev=4 
  before:  [ 4, 6, 6, 3, 5, 2 ]
  after:  [ 4, 4, 6, 3, 5, 2 ]

 prev=-1 
  2 loop End: 1,4,6,3,5,2

i=3 | target=3
 prev=2 | selectPrev=6 
  before:  [ 1, 4, 6, 3, 5, 2 ]
  after:  [ 1, 4, 6, 6, 5, 2 ]

 prev=1 | selectPrev=4 
  before:  [ 1, 4, 6, 6, 5, 2 ]
  after:  [ 1, 4, 4, 6, 5, 2 ]

 prev=0 
  3 loop End: 1,3,4,6,5,2

i=4 | target=5
 prev=3 | selectPrev=6 
  before:  [ 1, 3, 4, 6, 5, 2 ]
  after:  [ 1, 3, 4, 6, 6, 2 ]

 prev=2 
  4 loop End: 1,3,4,5,6,2

i=5 | target=2
 prev=4 | selectPrev=6 
  before:  [ 1, 3, 4, 5, 6, 2 ]
  after:  [ 1, 3, 4, 5, 6, 6 ]

 prev=3 | selectPrev=5 
  before:  [ 1, 3, 4, 5, 6, 6 ]
  after:  [ 1, 3, 4, 5, 5, 6 ]

 prev=2 | selectPrev=4 
  before:  [ 1, 3, 4, 5, 5, 6 ]
  after:  [ 1, 3, 4, 4, 5, 6 ]

 prev=1 | selectPrev=3 
  before:  [ 1, 3, 4, 4, 5, 6 ]
  after:  [ 1, 3, 3, 4, 5, 6 ]

 prev=0 
  5 loop End: 1,2,3,4,5,6

[ 1, 2, 3, 4, 5, 6 ]
**/

병합정렬

배열을 최소 단위 까지 분할 후, 부분 배열의 앞에서 부터 비교 삽입해 병합하는 방식으로 정렬한다.

  • 분할 정복 알고리즘의 하나

  • stable 정렬에 해당한다.

  • 시간 복잡도

    최악, 최선, 평균 O(n log n)
    빠른 정렬로 구분되는 정렬중 하나로, 일정한 시간복잡도를 가진다.

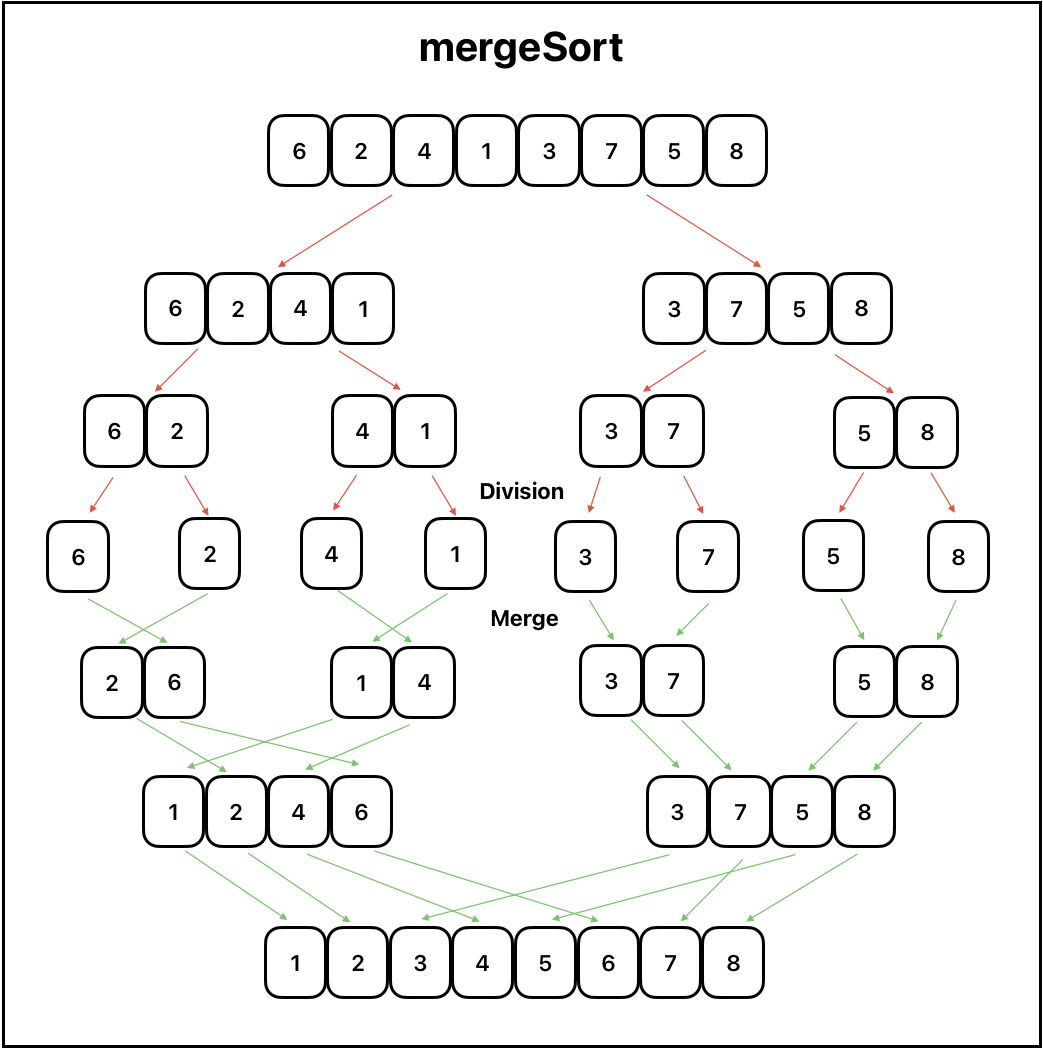
function merge(leftArr, rightArr) {
  const sortedArr = [];
  let l = 0;
  let r = 0;
  //console.log('arrays: ',leftArr,rightArr)
  while (l < leftArr.length && r < rightArr.length) {
    if (leftArr[l] <= rightArr[r]) {
      sortedArr.push(leftArr[l]);
      l++;
    } else {
      sortedArr.push(rightArr[r]);
      r++;
    }
  }
  while (l < leftArr.length) {
    sortedArr.push(leftArr[l]);
    l++;
  }
  while (r < rightArr.length) {
    sortedArr.push(rightArr[r]);
    r++;
  }
  //console.log('merge: ',sortedArr)
  return sortedArr;
}
let count=1;
function mergeSort(arr) {
  if (arr.length === 1) {
    return arr;
  }
  const mid = Math.ceil(arr.length / 2);
  const leftArr = arr.slice(0, mid);
  const rightArr = arr.slice(mid);
  //console.log('division: '+count,'|',leftArr, rightArr)
  count++
  return merge(mergeSort(leftArr), mergeSort(rightArr));
}
let newArr = [6,2,4,1,3,7,5,8];
console.log(mergeSort(newArr))

/**
division: 1 | [ 6, 2, 4, 1 ] [ 3, 7, 5, 8 ]
division: 2 | [ 6, 2 ] [ 4, 1 ]
division: 3 | [ 6 ] [ 2 ]

arrays:  [ 6 ] [ 2 ]
merge:  [ 2, 6 ]

division: 4 | [ 4 ] [ 1 ]

arrays:  [ 4 ] [ 1 ]
merge:  [ 1, 4 ]

arrays:  [ 2, 6 ] [ 1, 4 ]
merge:  [ 1, 2, 4, 6 ]

division: 5 | [ 3, 7 ] [ 5, 8 ]
division: 6 | [ 3 ] [ 7 ]

arrays:  [ 3 ] [ 7 ]
merge:  [ 3, 7 ]

division: 7 | [ 5 ] [ 8 ]

arrays:  [ 5 ] [ 8 ]
merge:  [ 5, 8 ]

arrays:  [ 3, 7 ] [ 5, 8 ]
merge:  [ 3, 5, 7, 8 ]

arrays:  [ 1, 2, 4, 6 ] [ 3, 5, 7, 8 ]
merge:  [1, 2, 3, 4, 5, 6, 7, 8]

[1, 2, 3, 4, 5, 6, 7, 8]
**/

퀵정렬

하나의 pivot(축)을 정해서 pivot보다 작은 값은 왼쪽에 큰값은 오른쪽에 위치시키는 방식의 정렬

재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

많이 사용되고 있는 정렬 알고리즘으로 대부분의 내장 라이브러리에서 존재하는 정렬 함수는 퀵 정렬 알고리즘을 사용한다.

  • 분할 정복 알고리즘 중 하나

  • Unstable 정렬에 해당한다.

  • 시간 복잡도

    최선, 평균 O(nlogn)
    최악(정렬이 되어 있는 경우) O(n^2)

    한 번 결정된 pivot들이 추후 연산에서 제외되는 특성 때문에, 시간 복잡도 O(nlogn)을 가지는 다른 정렬 알고리즘과 비교했을 때 가장 빠르다.

    일반적으로 준수한 효율을 보이지만 정렬된 배열에 대해서는 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.

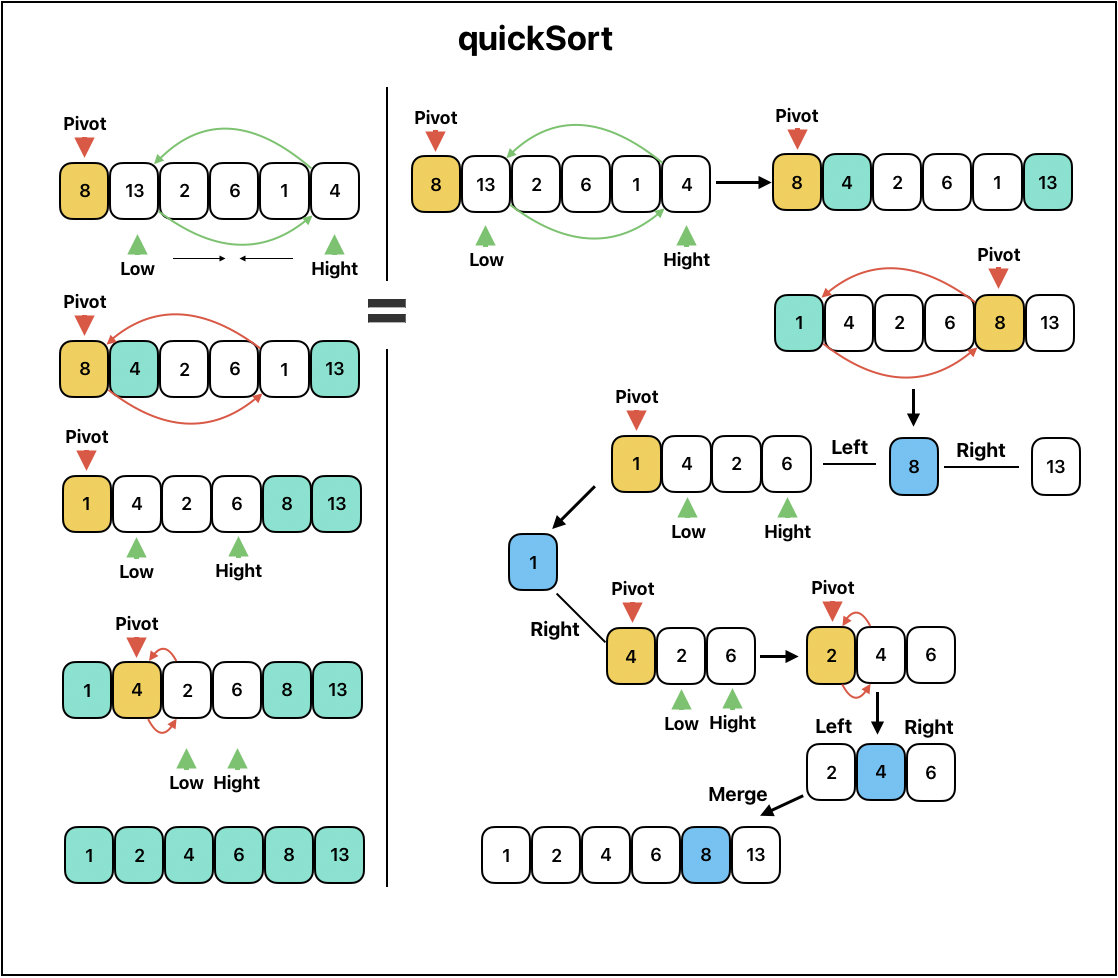
function quickSort(arr, left, right) {
  if (left >= right) {
    return;
  }

  let pivot = arr[left];
  let l = left;
  let r = right;
  //console.log('pivot='+pivot, 'l='+l, 'j='+j)
  //console.log('before: ',arr)
  while (l < r) {
    while (pivot < arr[r]) {
      r--;
    }
    while (l < r && pivot >= arr[l]) {
      l++;
    }
    [arr[l], arr[r]] = [arr[r], arr[l]];
    //console.log('inner: ',arr, 'l:'+l, 'r:'+r)
  }
  //console.log('after: ',arr, 'l:'+l, 'r:'+r)
  arr[left] = arr[l];
  arr[l] = pivot;
  //console.log('end: ',arr)
  quickSort(arr, left, l - 1);
  quickSort(arr, l + 1, right);
  return arr;
}
let newArr = [8,13,2,6,1,4];
console.log(quickSort(newArr, 0, newArr.length-1))

/*
pivot=8 l=0 r=5
before:  [ 8, 13, 2, 6, 1, 4 ]
inner:  [ 8, 4, 2, 6, 1, 13 ] i:1 j:5
inner:  [ 8, 4, 2, 6, 1, 13 ] i:4 j:4
after:  [ 8, 4, 2, 6, 1, 13 ] i:4 j:4
end:  [ 1, 4, 2, 6, 8, 13 ]

pivot=1 l=0 r=3
before:  [ 1, 4, 2, 6, 8, 13 ]
inner:  [ 1, 4, 2, 6, 8, 13 ] i:0 j:0
after:  [ 1, 4, 2, 6, 8, 13 ] i:0 j:0
end:  [ 1, 4, 2, 6, 8, 13 ]

pivot=4 l=1 r=3
before:  [ 1, 4, 2, 6, 8, 13 ]
inner:  [ 1, 4, 2, 6, 8, 13 ] i:2 j:2
after:  [ 1, 4, 2, 6, 8, 13 ] i:2 j:2
end:  [ 1, 2, 4, 6, 8, 13 ]

[ 1, 2, 4, 6, 8, 13 ]
*/

Reference

tistory-개발자 동쪽별-정렬 알고리즘(Sorting Algorithm) 정복하기 - with JS

inflearn-허민석-성공적인 코딩 인터뷰를 위한 코딩 인터뷰 정복하기 - 코딩 테스트

github.io-Heee's Development Blog-heejeong Kwon-[알고리즘] 퀵 정렬(quick sort)이란

profile
Rosevillage
이전 포스트

웹 접근성

다음 포스트

스택, 큐, 트리, 연결 리스트

0개의 댓글