이진 트리, 트리 순회방식

이진 트리

이진트리는 자식 노드를 2개 이하로 가지는 트리구조로
자식 노드는 각각 왼쪽노드, 오른쪽 노드라고 부르기도 한다.

자료를 처리하는 방법에 따라 크게 세 가지로 분류된다.

• 정 이진 트리 : 자식 노드가 2개나 없거나 둘중 하나의 상태를 가지는 이진 트리 구조
  

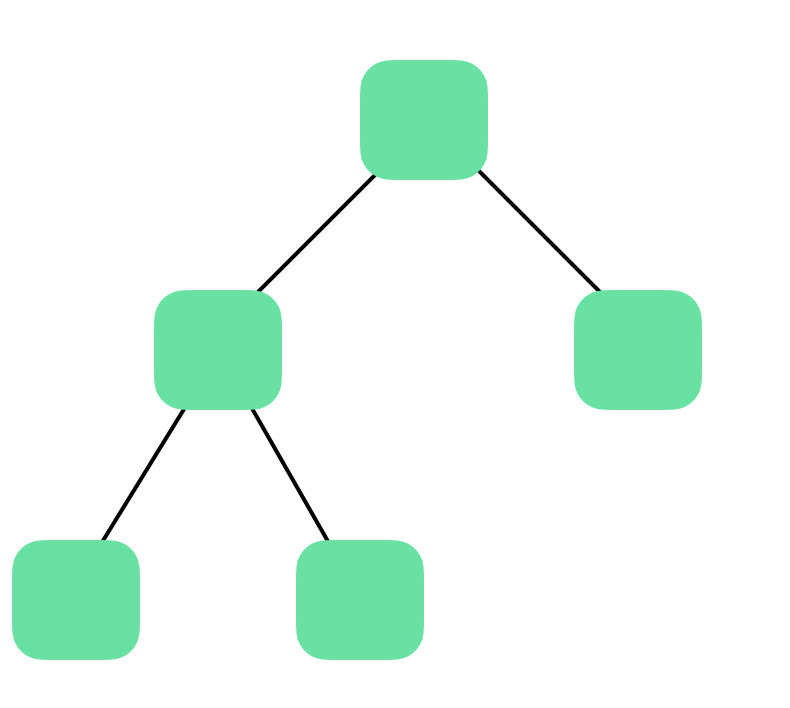
• 완전 이진 트리 : 마지막 레벨을 제외한 모든 노드가 가득 차 있는 이진 트리 구조, 마지막 레벨은 왼쪽부터 채워진다.
  

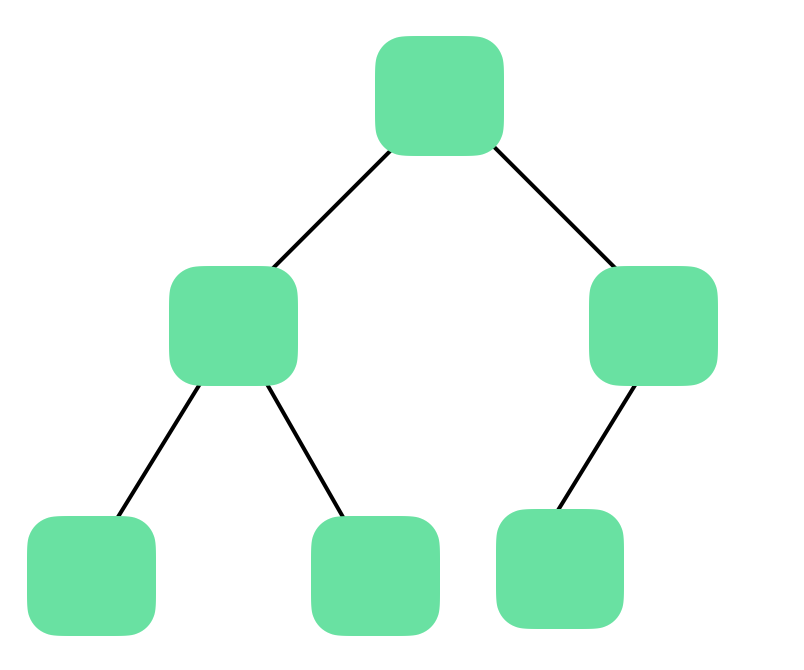
• 포화 이진 트리 : 모든 레벨의 노드가 가득 차 있는 이진 트리 구조
  

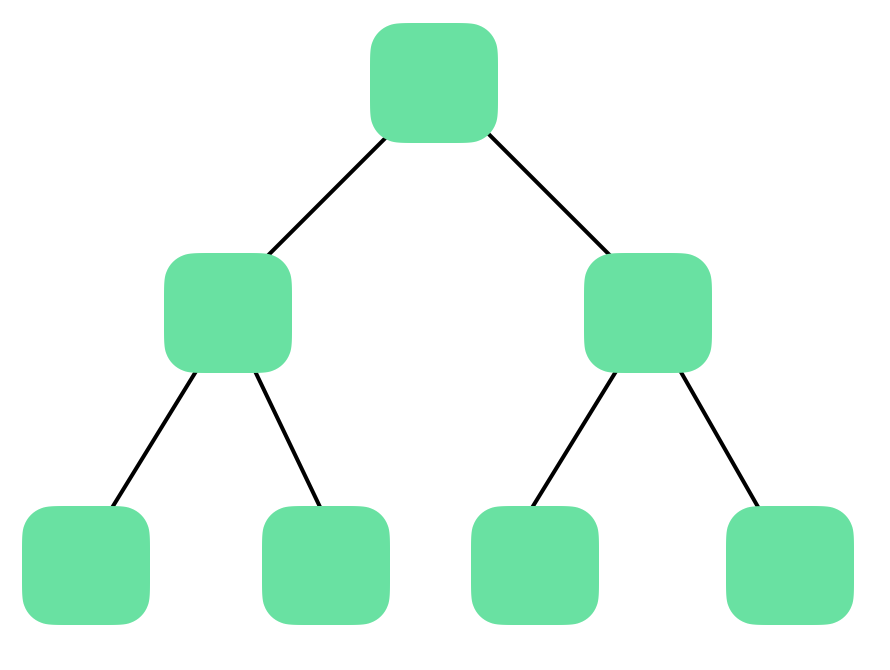
정렬된 트리

이진 탐색 트리(Binary Search Tree)

루트 노드의 값이 모든 노드의 값의 가운데 값인 형태의 이진 트리 구조로 부모노드는 자식 노드들의 가운데 값을 지니고, 왼쪽 노드는 더 작은 값, 오른쪽 노드는 더 큰 값을 지니고 있다.

또한 모든 노드는 중복되지 않는 고유한 값을 지니는데 트리의 한 종류라기 보다는 이진 탐색을 위해 조건에 맞는 트리를 만드는 방법에 가깝다.

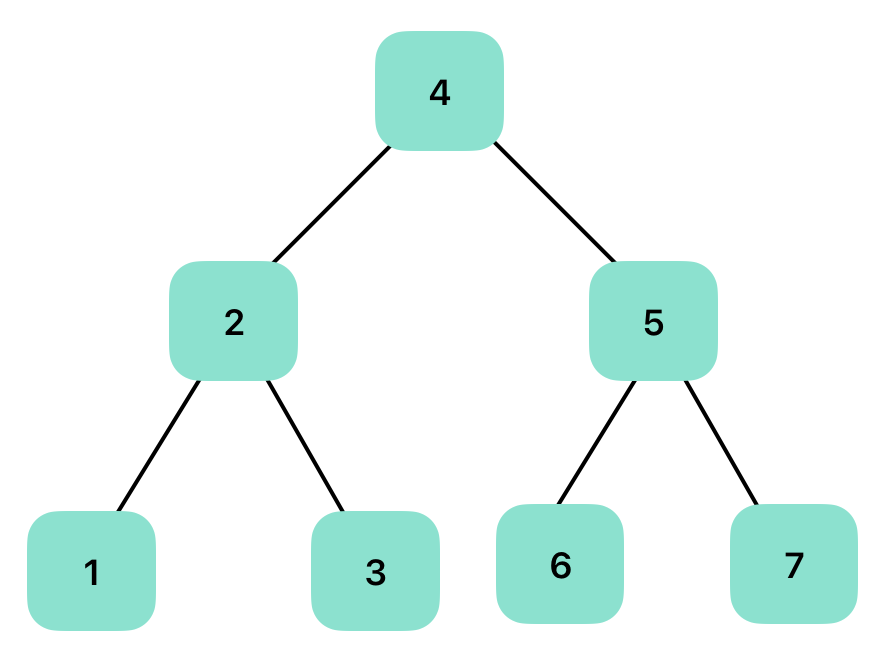
트리 순회

트리의 모든 노드에 접근해 값을 확인하는 것을 트리 순회하고 하며, 방식에 따라 크게 네가지로 나뉜다.

• 전위 순회
  루트(부모)노드로부터 시작해서, 왼쪽 노드, 오른쪽 노드 순서로 접근하는 순회 방식으로, 주로 트리를 복사할 때 사용한다.
  
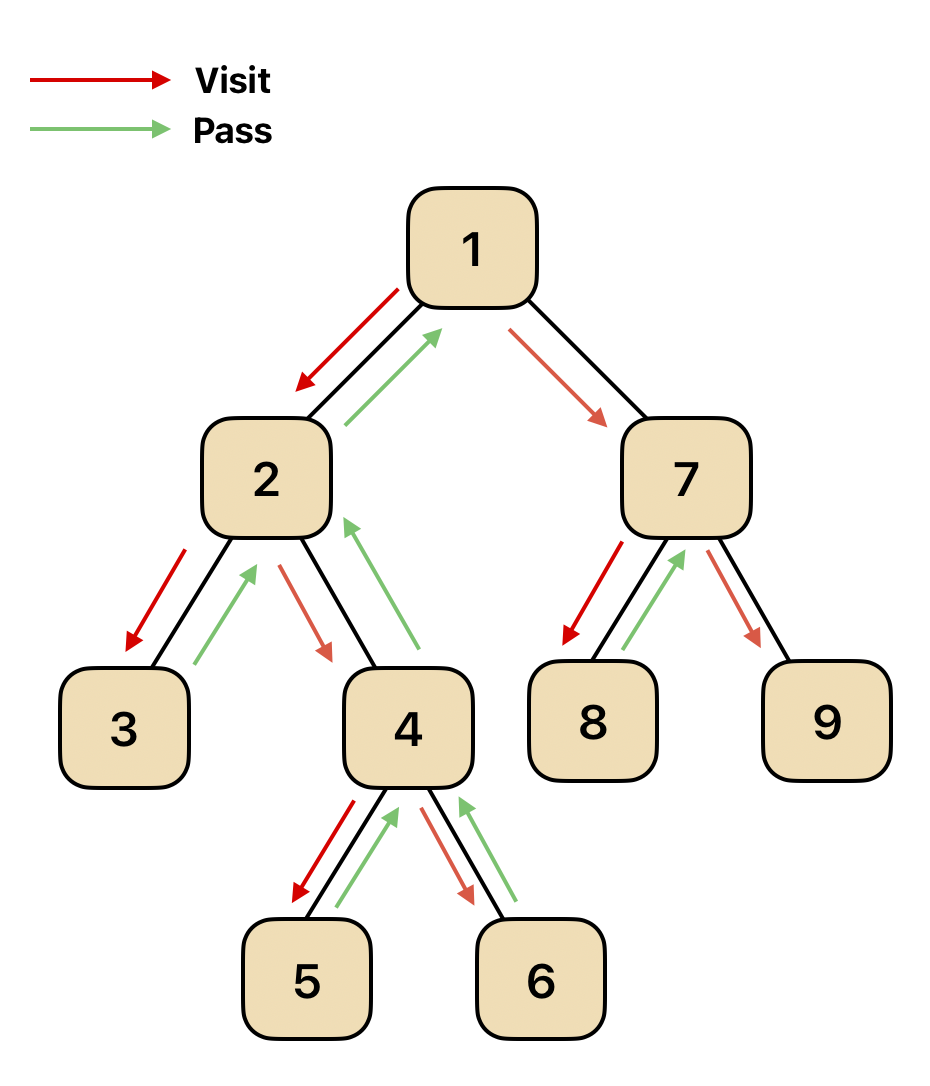
  재귀를 통해 다음과 같이 구현할 수 있다.

  class Node {
   constructor(val = 0, left = null, right = null) {
   this.val = val;
   this.left = left;
   this.right = right;
   }
  }
  let answer=[]
  const preOrder=(node)=> {
   if(!node) return;
   answer.push(node.val); // 부모 노드부터 순회
   if(node.left) preOrder(node.left); // 왼쪽 노드 탐색
   if(node.right) preOrder(node.right); // 오른쪽 노드 탐색
  }
  
  const root1 = new Node(5, new Node(13, new Node(35), new Node(8)), new Node(21));
  //         5
  //        / \
  //       13 21
  //      / \
  //     35  8
  preOrder(root1);
  console.log(answer) // [5,13,35,8,21]

• 중위 순회
  왼쪽 노드로부터 시작해서 부모 노드, 오른쪽 노드 순서로 접근하는 순회 방식으로, 주로 이진 탐색 트리의 오름차순 값을 얻어올 때 사용한다.
  
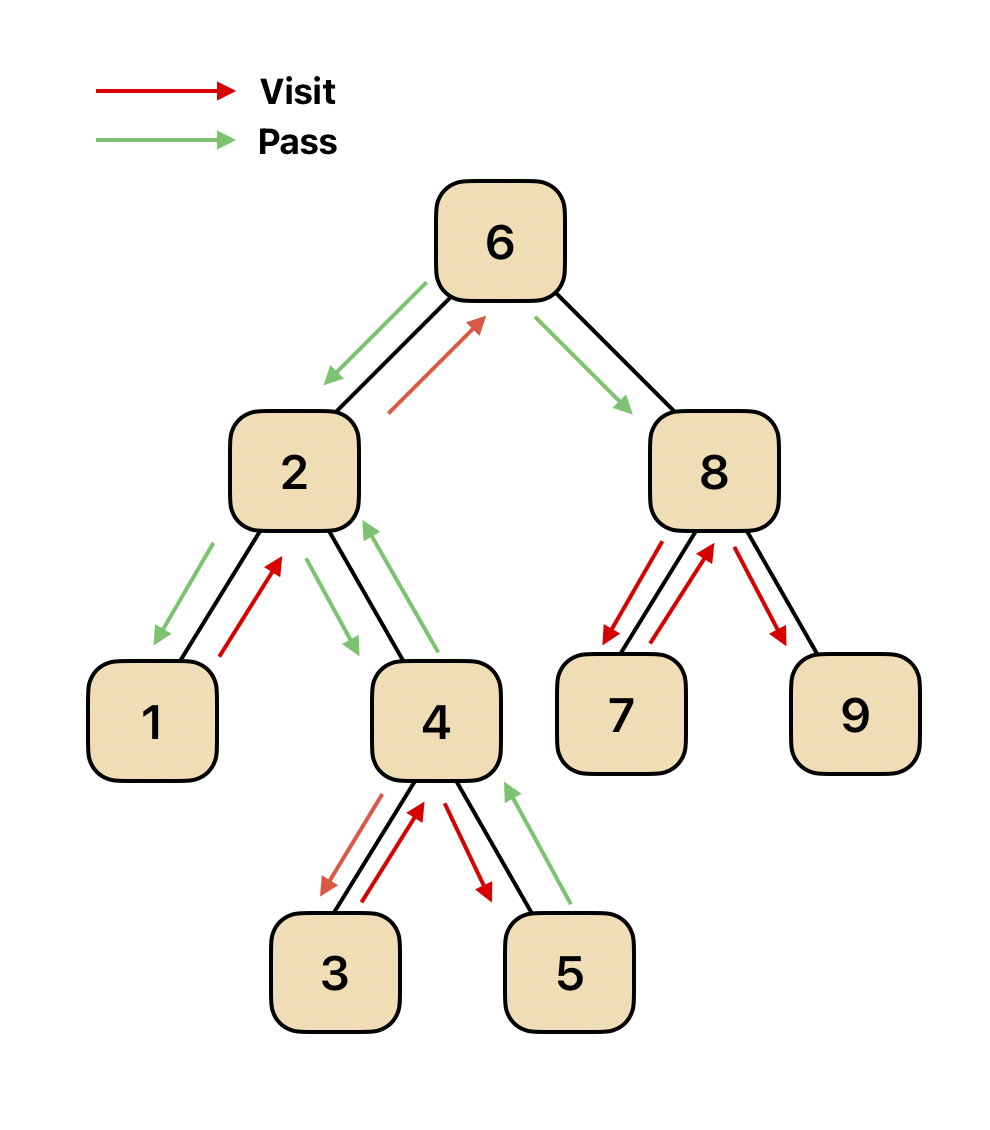
  재귀를 통해서 다음과 같이 구현할 수 있다.

  class Node {
   constructor(val = 0, left = null, right = null) {
   this.val = val;
   this.left = left;
   this.right = right;
   }
  }
  let answer=[]
  const inOrder=(node)=> {
   if(!node) return;
   if(node.left) inOrder(node.left);
   answer.push(node.val);
   if(node.right) inOrder(node.right);
  }
  
  const root = new Node(5, new Node(13, new Node(35), new Node(8)), new Node(21));
  //         5
  //        / \
  //       13 21
  //      / \
  //     35  8
  inOrder(root);
  console.log(answer) // [35,13,8,5,21]

• 후위 순회
  윈쪽 노드로 부터 시작해서, 오른쪽 노드, 부모 노드 순서로 접근하는 순회방식으로, 주로 트리를 삭제할 때 시용된다.
  
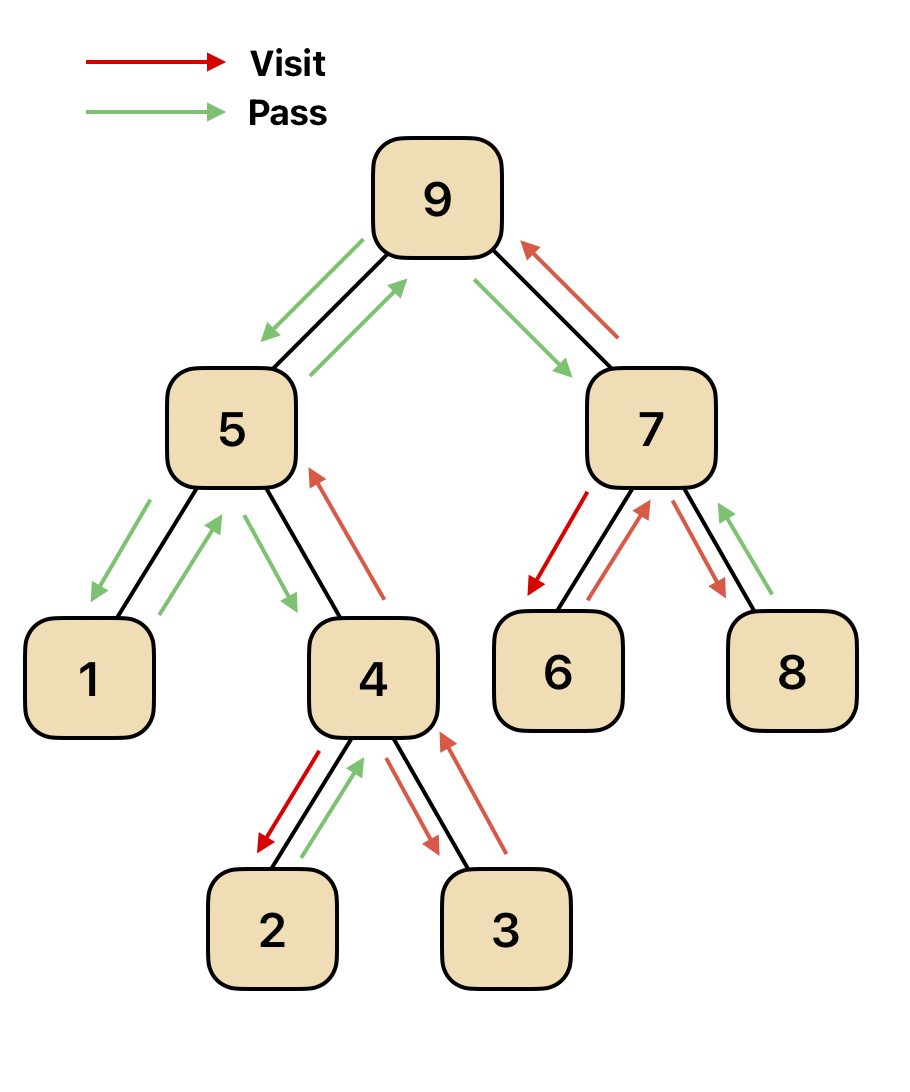
  재귀를 통해서 다음과 같이 구현할 수 있다.

  class Node {
   constructor(val = 0, left = null, right = null) {
   this.val = val;
   this.left = left;
   this.right = right;
   }
  }
  let answer=[]
  const postOrder=(node)=> {
   if(!node) return;
   if(node.left) postOrder(node.left);
   if(node.right) postOrder(node.right);
   answer.push(node.val);
  }
  
  const root = new Node(5, new Node(13, new Node(35), new Node(8)), new Node(21));
  //         5
  //        / \
  //       13 21
  //      / \
  //     35  8
  postOrder(root);
  console.log(answer) // [35,8,13,21,5]

• 레벨 순회
  트리의 레벨을 기준으로 노드들에 접근하는 순회 방식으로, 같은 층의 노드를 왼쪽에서 오른쪽으로 모두 탐색한 다음, 다음 층으로 이동한다.
  

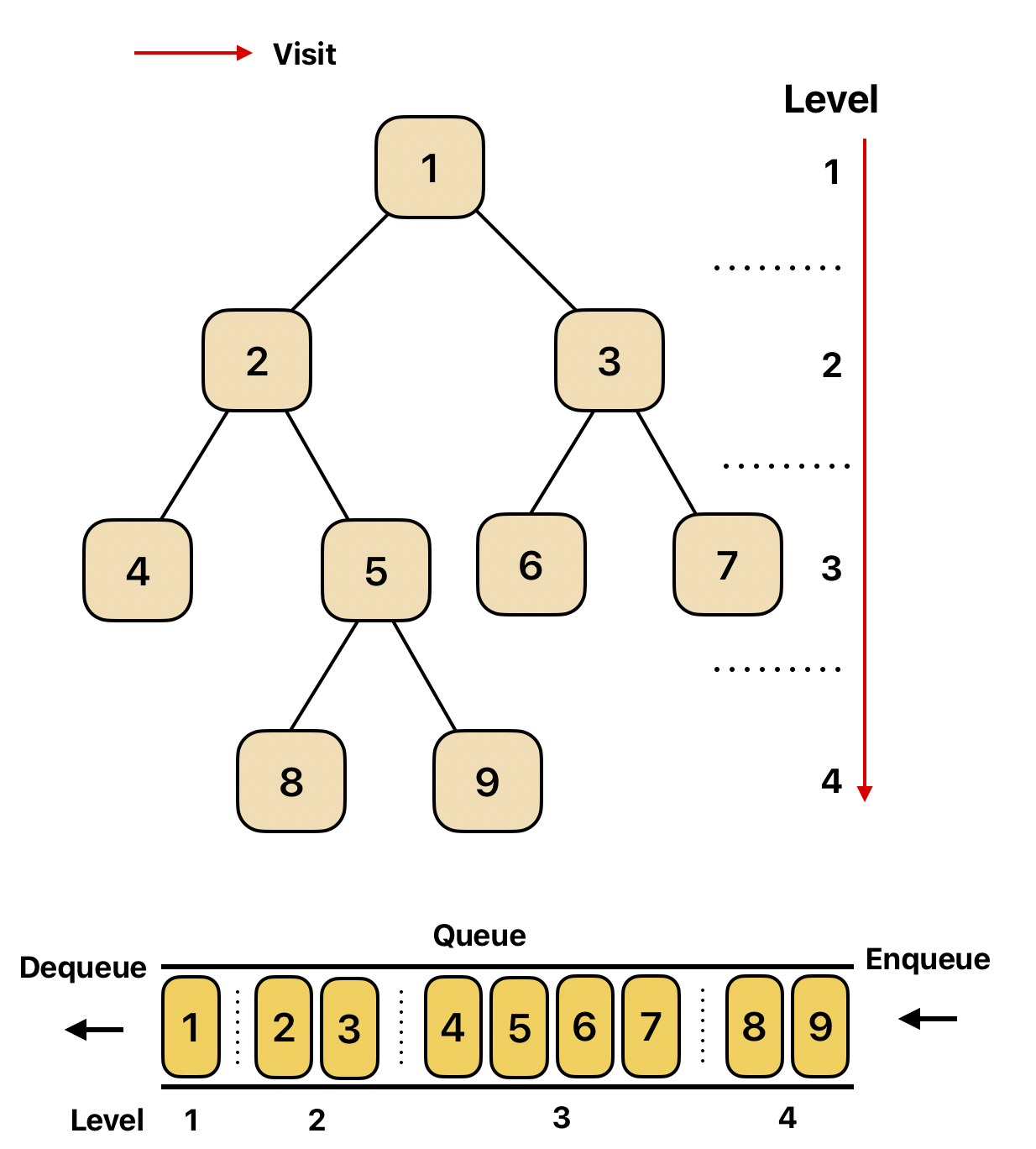
  반복문을 통해 다음과 같이 구현할 수 있다.

  class Node {
   constructor(val = 0, left = null, right = null) {
   this.val = val;
   this.left = left;
   this.right = right;
   }
  }
  
  const levelOrder=(node)=> {
   const result=[];
   if(!node) return result;
   
   const queue=[node];
   
   while(queue.length>0) {
     const leng=queue.length;
     
     for(let i=0;i<leng;i++) {
       const curNode = queue.shift()
       result.push(curNode.val)
       if(curNode.left) queue.push(curNode.left)
       if(curNode.right) queue.push(curNode.right)
     }
   }
   return result
  }
  
  const root = new Node(5, new Node(13, new Node(35), new Node(8)), new Node(21));
  //         5
  //        / \
  //       13 21
  //       / \
  //      35  8
  console.log(levelOrder(root)) // [5, 13, 21, 35, 8]

이 네가지 순회 방식은 또 둘로 나눌 수 있다.

• 재귀로 작성하기 쉽고, 우선적으로 마지막 레벨에 도달하는 과정을 가지는 방식

  dfs(Depth-First Search)[깊이 우선 탐색]에 가깝다.

  • 전위 순회
  • 중위 순회
  • 후위 순회

• 큐를 통해 작성하기 쉽고, 마지막 레벨을 나중에 도달하는 과정을 가지는 방식

  bfs(Breadth-First Search)[너비 우선 탐색]에 가깝다.

  • 레벨 순회