힙(Heap)과 힙 정렬

힙(Heap)

이진 트리(binaly tree)를 기반으로 하는 자료구조로, 최댓값과 최소값을 빠르게 얻어내기 위해 고안되었다.
힙은 크게 두가지 종류로 나뉜다.

• 최대 힙 : 부모 노드의 값이 자식보다 크다는 규칙을 가지는 경우
• 최소 힙 : 부모 노드의 값이 자식보다 작다는 규칙을 가지는 경우

힙의 root노드가 최댓값/최솟값을 가지는 특성을 활용해 우선순위 큐 같은 자료구조를 만들 수도 있다.

힙 정렬

힙을 이용해 정렬을 하는 방식으로, 주어진 배열을 오름차순으로 정렬할 경우 최대 힙으로 변환한 다음 루트 노드를 가장 뒤쪽으로 보내는 방식으로 정렬한다.

힙을 만드는 과정에서 O(n), 힙을 정렬하는 과정에서 O(n log n)의 시간복잡도를 가지기 때문에
힙 정렬 전체의 시간복잡도는 최악, 최선, 평균 O(n log n)으로 나타난다.

배열을 힙 트리로 변환하는 과정을 heapify라고하며, 최대 힙의 경우 부모 노드의 값이 자식보다 커지는 것을 목표로 동작한다.

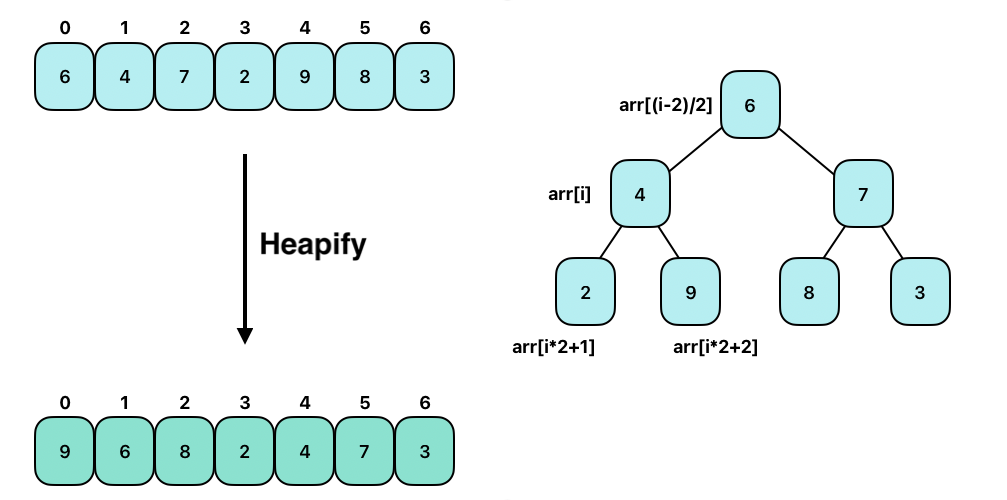
자식을 가지는 마지막 자식 노드부터 시작해서, 루트 노드까지 이동하며, 부모 노드가 자식 노드보다 크도록 만드는 과정을 통해 최대 힙을 생성한다.

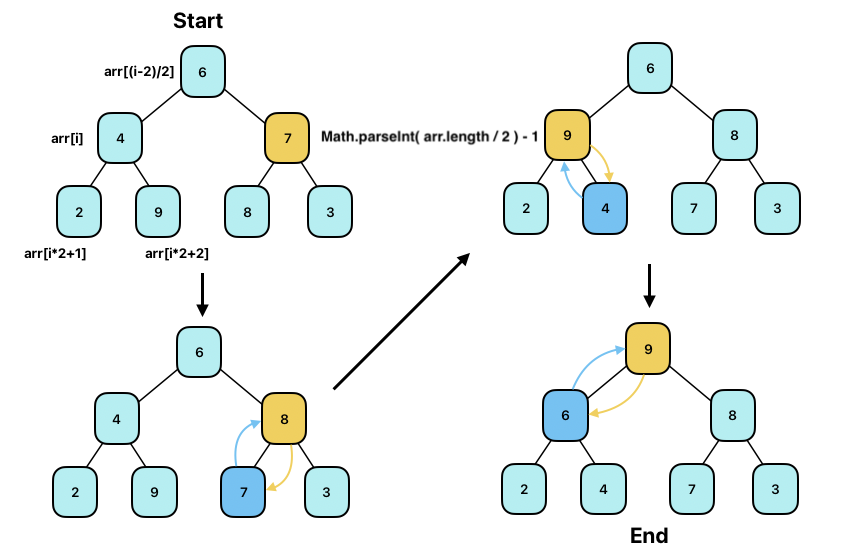
위의 그림의 동작을 코드로 변환해보면 다음과 같다.

function makeHeap(arr) {
  const copy = arr.slice();
  let leng = copy.length - 1;
  let p = parseInt(leng / 2);
  while (p >= 0) {
      heapify(copy, p, leng);
      p--;
  }
  return copy;
}

function heapify(arr, i, limit) {
  let l = i * 2 + 1;
  let r = i * 2 + 2;
  let p = i;

  if((l <= limit && arr[l] && arr[l] > arr[p]) || (r <= limit && arr[r] && arr[r] > arr[p])) {
      p = r <= limit && arr[r] && arr[r] > arr[l] ? r : l;
      [arr[p], arr[i]] = [arr[i], arr[p]];
      heapify(arr, p, limit);
  }
}

let target = [6, 4, 7, 2, 9, 8, 3];

makeHeap(target);
// heapify: [6, 4, 8, 2, 9, 7, 3]
// heapify: [6, 9, 8, 2, 4, 7, 3]
// heapify: [9, 6, 8, 2, 4, 7, 3]
// heapify: [9, 6, 8, 2, 4, 7, 3]

힙이 만들어지면
다음과 같은 단계를 통해 정렬한다.

• 루트 노드의 값과 마지막 노드의 값을 교환한다.
• 변경된 마지막 노드를 제외한 나머지 노드들의 힙을 다시 구성한다.
• 위 두 단계를 반복하다가 정렬이 완료되면 종료한다.

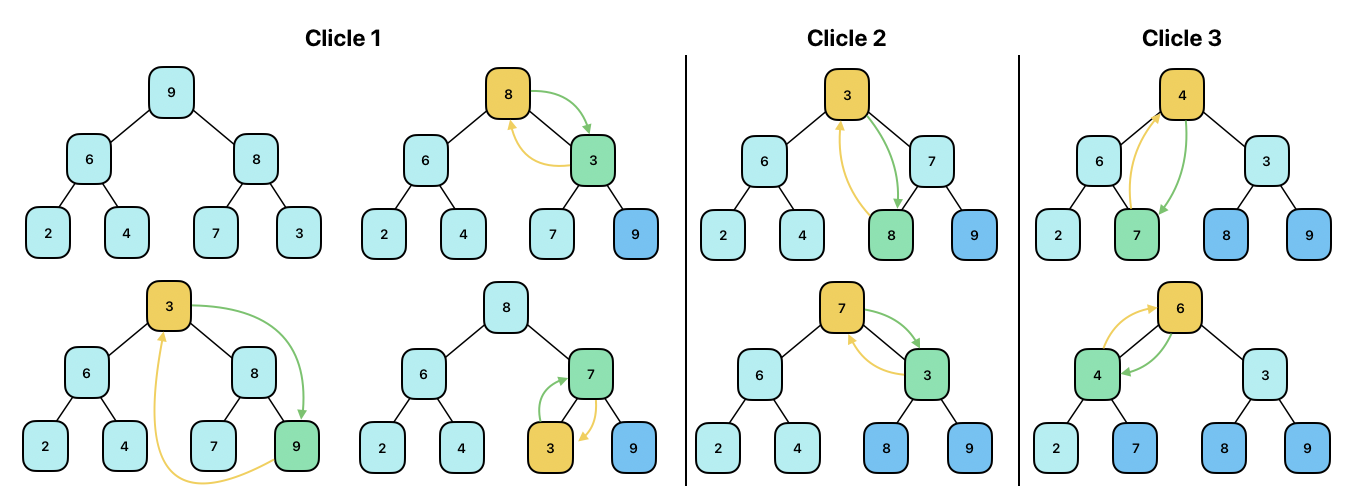
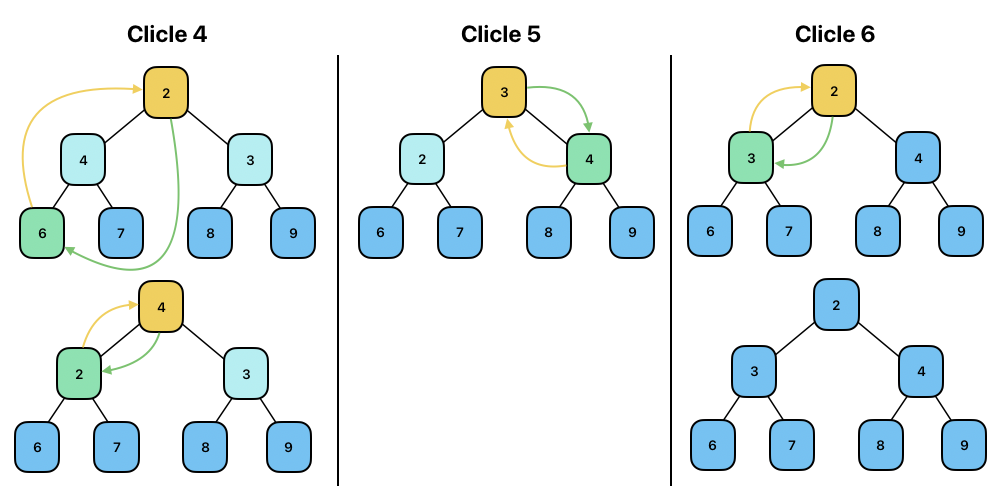
그림의 동작을 다음과 같이 구현해 볼 수도 있다.

function heapSort(arr) {
  const copy = arr.slice()
  const length = copy.length
  
  if (length === 1) return copy
  
  let end = length - 1
  while (end > 0) {
    let temp = copy[0];
    copy[0] = copy[end]
    copy[end] = temp;
    end--
    heapify(copy, 0, end) 
  }
  return copy
}

// 힙으로 만들어진 target은 다음과 같은 모습을 하고 있다. [9, 6, 8, 2, 4, 7, 3]

heapSort(target);
// [9, 6, 8, 2, 4, 7, 3]
// swap:  [3, 6, 8, 2, 4, 7, 9] 
// heapify:  [8, 6, 7, 2, 4, 3, 9]

// swap:  [3, 6, 7, 2, 4, 8, 9]  
// heapify:  [7, 6, 3, 2, 4, 8, 9]

// swap:  [4, 6, 3, 2, 7, 8, 9]   
// heapify:  [6, 4, 3, 2, 7, 8, 9]

// swap:  [2, 4, 3, 6, 7, 8, 9]  
// heapify:  [4, 2, 3, 6, 7, 8, 9]

// swap:  [3, 2, 4, 6, 7, 8, 9]  
// heapify:  [3, 2, 4, 6, 7, 8, 9]

// swap:  [2, 3, 4, 6, 7, 8, 9] 
// heapify:  [2, 3, 4, 6, 7, 8, 9]