분리 집합(Union-Find)

Union-Find

분리 집합(Union-Find)은 두 노드가 같은 집합에 속하는지 확인하는 그래프 알고리즘이다

노드를 합치는 Union 알고리즘과, 노드가 집합에 있는지 확인하는 Find 알고리즘으로 이루어진다

동작 과정

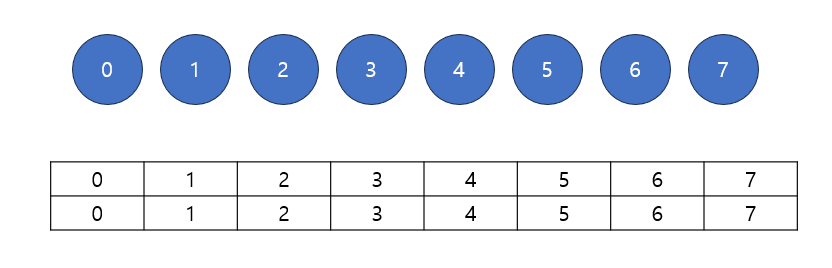
[1717] 집합의 표현 문제의 예제를 통해 동작 과정을 확인해보자

초기에 서로 분리되어있는 8개의 노드가 있고, 각 노드의 부모는 자기자신이 된다

(1) 1과 3을 합치기

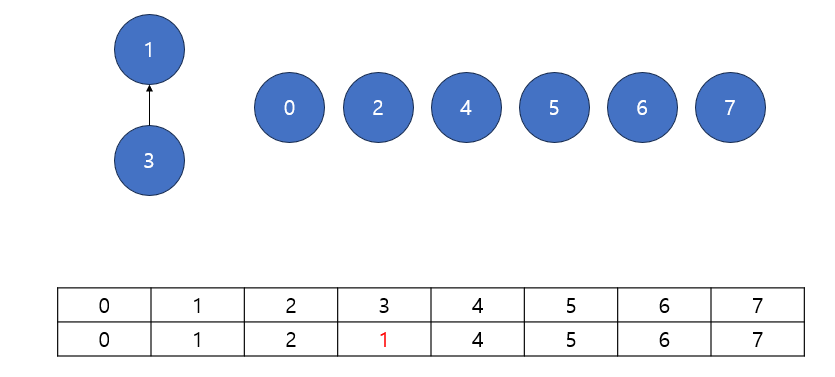
위 상황과 같이 1번 노드의 부모와, 3번 노드의 부모를 찾은 다음

한 노드의 부모를 다른 노드의 부모 노드 값으로 갱신한다
(이때, 일관성있게 기록하도록 부모 노드 값이 작은 쪽으로 갱신을 시켰다)

(2) 1과 7번이 같은 집합에 있는지 확인

1의 부모는 1이며, 7의 부모는 7이므로 서로 다른 부모를 가리키기때문에 같은 집합에 있지 않다

(3) 7과 6을 합치기

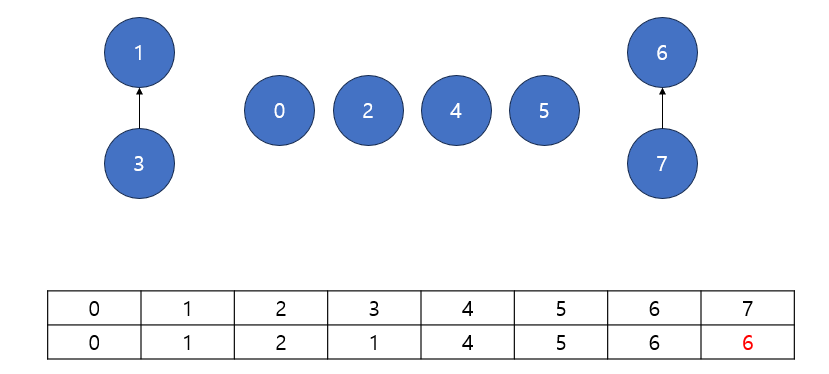
(1) 과정과 동일하다

(4) 7과 1이 같은 집합에 있는지 확인

7의 부모는 6으로 갱신되었지만, 여전히 1의 부모는 1로 서로 다르기때문에 같은 집합에 있지 않다

(5) 3과 7을 합치기

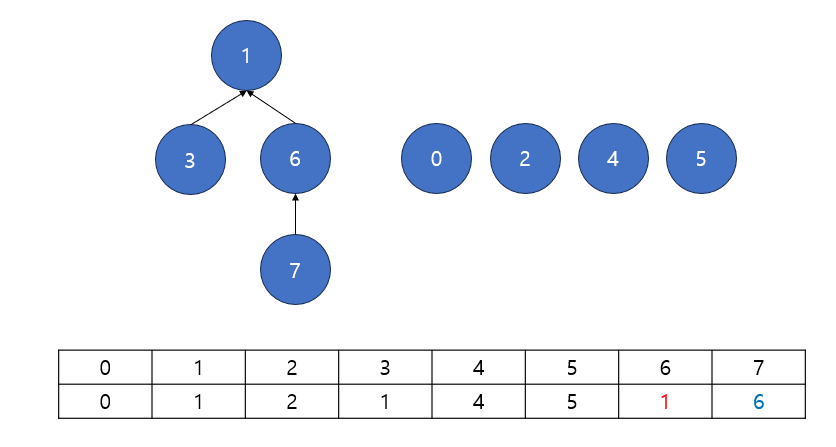
7의 부모 6, 3의 부모 1에 대해 6은 부모로 1을 갖게 된다

그러나 여기까지만 기록한 후 7과 다른 어떤 노드를 합치려고하면, 7의 부모 6에서 다시 6의 부모 1로 거쳐가게 되기 때문에 비효율적으로 동작하게 된다

따라서 7또한 부모로 1을 가짐을 기록하게 해야하며, 이것이 경로 압축이 된다

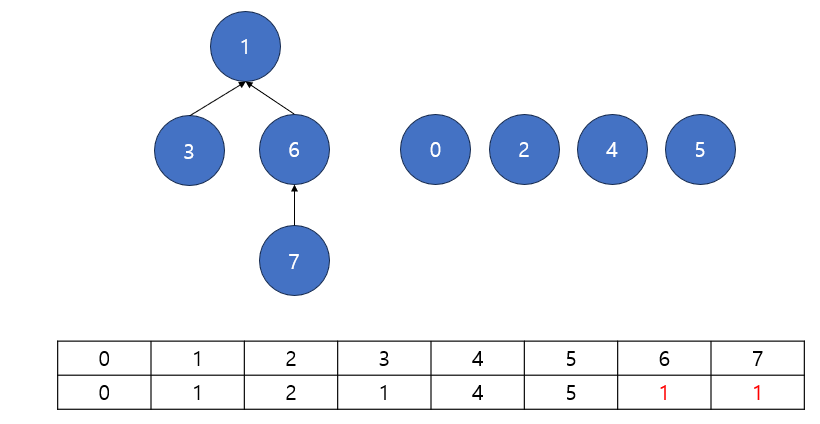
이후의 과정은 앞의 과정과 동일하므로 생략한다

[1717] 집합의 표현 문제를 풀어보며 union-find를 구현해보면 다음과 같다

코드

import sys
sys.setrecursionlimit(100000)
input = sys.stdin.readline

def find_parent(target):
    if target == pointer[target]: return target # 자기자신
    
    pointer[target] = find_parent(pointer[target])
    return pointer[target]

def union(x, y):
    x = find_parent(a)
    y = find_parent(b)

    if x == y: return # 같은 부모에 연결되어있음

    if x < y: pointer[y] = x # 더 작은 값이 루트가 된다
    else: pointer[x] = y 

def is_union(x, y):
    x = find_parent(a)
    y = find_parent(b)

    if x == y: return True
    else: return False

n, m = map(int, input().split())
pointer = [i for i in range(n+1)] # 처음엔 자기자신을 지목
for _ in range(m):
    q, a, b = map(int, input().split())

    if q == 0: union(a, b)
    else: 
        if is_union(a, b): print('YES')
        else: print('NO')

부모를 찾는 과정을 재귀를 통해 진행했으며,
부모를 찾고 돌아오는 과정에서 이전에 방문했던 모든 노드들을 return된 부모의 값으로 저장해줌으로써 경로 압축을 진행했다