플로이드-워셜(Floyd-Warshall)

플로이드-워셜(Floyd-Warshall)

플로이드-워셜 알고리즘은 변의 가중치가 음이거나 양인 가중 그래프에서 최단 경로들을 찾는 알고리즘이다

알고리즘을 한 번 수행하면 모든 꼭짓점 쌍 간의 최단 경로의 길이을 찾는다

모든 정점 쌍 사이의 최단경로를 구할 때 최대로 구해야할 경우의 수는 $n^2$개이다 (자신으로 돌아오는 경로까지 모두 포함)

작동 방식은 다음과 같다

1. 한 정점(s)에서 다른 정점(e)로 갈 때, 중간 정점(k)를 거쳐갈 때 나오는 최단 경로를 계산한다

2. 각 k에 대해 1의 과정을 모든 가능한 쌍 (s, e)에 대해 진행한다

이때 k의 횟수는 정점의 개수 V개 만큼 반복이 된다

이 이유는 벨만-포드 알고리즘에서 설명된 것과 같다

따라서 어느 정점을 순서 상관없이 방문하며 갱신을 진행해도 최종적으로 최단 경로가 갱신이 된다

플로이드-워셜 알고리즘은 동적 계획법 알고리즘이기도 하다

다익스트라 알고리즘이나 벨만-포드 알고리즘은 각 정점(s, e) 간의 최단 경로를 찾아가는 방식으로 진행된다

반면에 플로이드-워셜 알고리즘은 중간 정점(k)을 통해 계산된다

하나의 큰 문제를 여러 작은 문제로 쪼개고 중복된 연산을 방지하기 위해 작은 문제의 답을 저장해나가는 동적 계획법 특징을 생각해보면, 하나의 큰 문제 s → e의 최단 경로를 s → k, k → e로 나누면서 각각의 최단 경로를 저장해 나가고, 그것을 종합하여 s → e의 한 문제를 해결해낸다

동작 과정

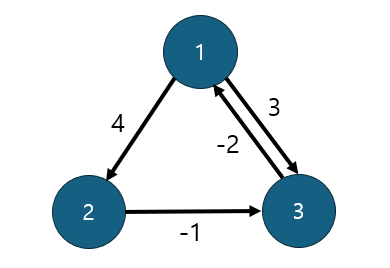
다음 그래프를 통해 작동 과정을 확인해보자

먼저 반복을 시작하기 전 테이블의 최단 경로 값은 2차원 테이블로 작성한다
행은 시작점 s, 열은 종점 e 라고 하자

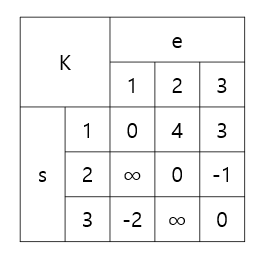
이제 중간 정점 K를 1부터 3까지 반복하며 최단 경로를 갱신해보자

1. K = 1

   • (1, 1): 자기자신은 0이다

   • (1, 2): 1에서 1을 거쳐(0), 2로 가는 경우(4)는 이미 4로 갱신되어 있다

   • (1, 3): 1에서 1을 거쳐(0), 3으로 가는 경우(3)는 이미 3으로 갱신되어 있다

   • s = 2: 2에서 1을 거치는 경로는 없으므로 INF로 남겨놓는다

   • (3, 1): 3에서 1을 거쳐(-2), 1로 가는 경우(0)는 이미 -2로 갱신되어 있다

   • (3, 2): 3에서 1을 거쳐(-2), 2로 가는 경우(4)는 총합 2이므로 2로 갱신한다

   • (3, 3): 3에서 1을 거쳐(-2), 3으로 가는 경우(3)는 총합 1이지만, 이미 0으로 갱신되어있어 그대로 유지한다

   여기까지 K = 1에 대해 모든 반복이 종료된다

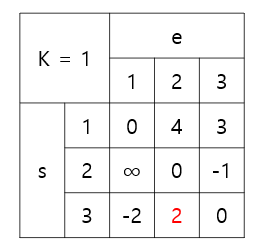
이 과정을 K = 2에 대해 진행하면 다음과 같다

2. K = 2

   • (1, 1): 1에서 2를 거쳐(4), 1로 가는 경우(INF)는 여전히 없다

   • (1, 2): 1에서 2를 거쳐(4), 2로 가는 경우(0)는 여전히 4이다

   • (1, 3): 1에서 2를 거쳐(4), 3으로 가는 경우(-1)는 여전히 3이다

   • (2, 1): 2에서 2를 거쳐(0), 1로 가는 경우(INF)는 여전히 없다

   • (2, 2): 자기자신은 0이다

   • (2, 3): 2에서 2를 거쳐(0), 3으로 가는 경우(-1)는 여전히 -1이다

   • (3, 1): 3에서 2를 거쳐(2), 1로 가는 경우(INF)는 여전히 없다

   • (3, 2): 3에서 2를 거쳐(2), 2로 가는 경우(0)는 여전히 2이다

   • (3, 3): 3에서 2를 거쳐(2), 3으로 가는 경우(-1)는 1이지만, 이미 0으로 갱신되어 있다

   여기까지 K = 2에 대해 모든 반복이 종료된다

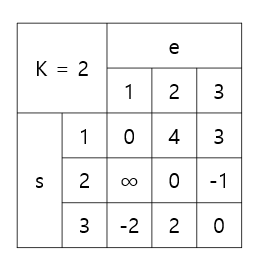
마지막으로 K = 3에 대해 진행하면 다음과 같다

3. K = 3

   • (1, 1): 1에서 3을 거쳐(3), 1로 가는 경우(-2)는 1이지만 이미 0으로 갱신되어 있다

   • (1, 2): 1에서 3을 거쳐(3), 2로 가는 경우(2)는 5이지만 이미 4로 갱신되어 있다

   • (1, 3): 1에서 3을 거쳐(3), 3으로 가는 경우(0)는 여전히 3이다

   • (2, 1): 2에서 3을 거쳐(-1), 1로 가는 경우(-2)는 총합 -3으로 드디어 2에서 1로 가는 최단 경로를 갱신하게 되었다!

   • (2, 2): 2에서 3을 거쳐(-1), 2로 가는 경우(2)는 1이지만 이미 0으로 갱신되어 있다

   • (2, 3): 2에서 3을 거쳐(-1), 3으로 가는 경우(0)는 여전히 -1이다

   • (3, 1): 3에서 3을 거쳐(0), 1로 가는 경우(-2)는 여전히 -2이다

   • (3, 2): 3에서 3을 거쳐(0), 2로 가는 경우(2)는 여전히 2이다

   • (3, 3): 자기자신은 0이다

   여기까지 K = 3에 대해 모든 반복이 종료된다

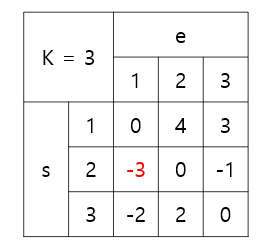
이렇게 각 시점에서 각 종점까지의 최단경로 테이블이 완성되었다!

음수 사이클

위에서 예시를 든 것과 같이 음수 가중치가 있는 그래프에서도 작동하는 것이 특징인데, 플로이드-워셜 알고리즘은 음수 사이클을 거치면 어떤 테이블 결과가 나타날까?

위에서 든 예시 그래프를 조금 바꿔 음수 사이클이 생기게 만들었다

다시 테이블을 만들고 각 K에 대해 채워보자

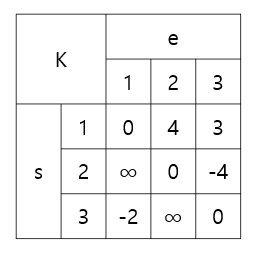
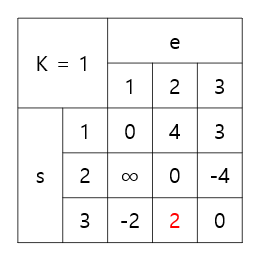
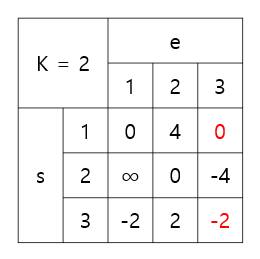
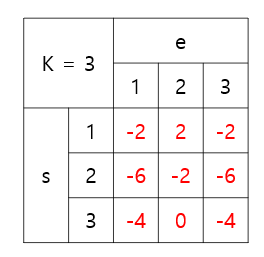
위 테이블과 같이 변했는데, 자기자신이었던 s = e의 경우가 음수로 갱신되었다!

직관적으로 생각해볼때, s에서 여러 정점을 돌고돌아 다시 s로 돌아오면 가중치를 타고 거리값이 양수나 0이 될 것이고 갱신은 되지 않는다

그러나 돌고돌아 음수로 돌아오는 경로가 존재하면 그 경로의 모든 정점은 -∞으로 발산하게 되고, 이것은 음수 사이클이 발생한다는 것을 의미한다

따라서 플로이드-워셜 알고리즘 진행 중에 (s, s) 인 쌍이 어느것 하나라도 0에서 음수로 갱신된다면, 음수 사이클이 존재한다는 것을 검증할 수 있다!

시간복잡도

각 k에 대해, 그리고 각 정점 쌍(s, e)에 대해 반복이 되므로 k가 1부터 V까지, s가 1부터 V까지, e가 1부터 V까지의 경우를 모두 반복하게 되어 코드로 구현하게 되면 삼중 반복문이 만들어진다

따라서 $O(V^3)$의 시간복잡도를 갖게 된다