1. Amdahl's law(암달의법칙)
암달의 법칙(Amdahl's law)은 암달의 저주로도 불리며 컴퓨터 시스템의 일부를 개선할 때 전체적으로 얼마만큼의 최대 성능 향상이 있는지 계산하는 데 사용됩니다. 진 암달의 이름에서 따왔습니다.
보통은 암달의 법칙은 프로세서 개수에 따라 시스템 성능이 어느정도 향상되는지 보여주는 그래프로 많이 설명합니다.
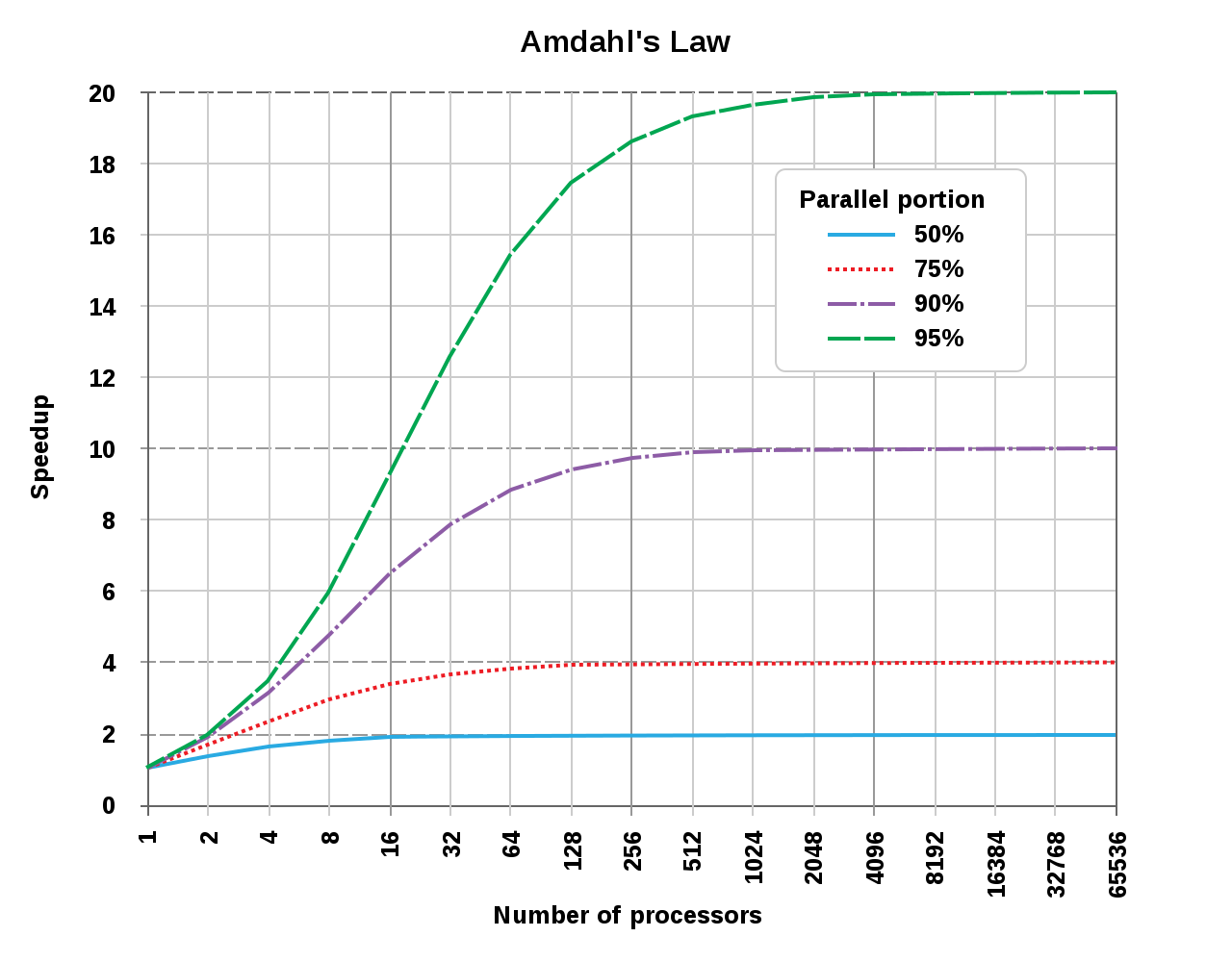
프로그램은 병렬처리가 가능한 부분과 불가능한 순차적인 부분으로 구성되므로 프로세서를 아무리 병렬화 시켜도 더 이상 성능이 향상되지 않는 한계가 존재합니다.
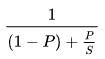
계산하는 공식은 다음과 같습니다. 1-P는 병렬처리가 불가능한 부분이고, P는 병렬처리가 가능한 부분입니다. S는 프로세서 개수입니다.
예를 들어 병렬처리가 가능한 부분이 95% 라고 해보겠습니다. 그렇다면 S를 무한대로 놓고 최대로 속도향상이 가능한 임계점을 계산해보면 1/(1-0.95) = 20 이 됩니다. 즉, 최대한 프로세서를 늘려봤자 20배가 마지노선 이라는 뜻이 됩니다.
만약 프로세서의 개수가 20개이고 병렬처리가 가능한 부분이 95% 라면? 1/{(1-0.95)+(0.95/20)} = 10.25가 됩니다. 10.25배 향상이 가능하다는 소리입니다.
2. Gustafson's Law(구스타프슨 법칙)
구스타프슨의 법칙(Gustafson's Law)은 컴퓨터 과학에서 대용량 데이터 처리는 효과적으로 병렬화할 수 있다는 법칙입니다.
암달의 법칙이 일의 양을 정해놓고 실행시간 감소에 초점을 두었다면 구스타프슨의 법칙은 일의 양을 정해놓지 않고 동일한 시간 동안의 작업분량에 초점을 두었습니다. 즉, 암달의 법칙은 latency에, 구스타프슨의 법칙은 throughput에 기준을 두었다고 보면 됩니다.
두 법칙은 서로 대립되는 느낌이지만 관점이 다르기 때문에 대립된다고는 볼 수 없을 듯합니다.
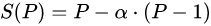
여기에서 P는 프로세서의 개수, a는 병렬화되지 않는 부분의 비율, S(P)는 이론상 성능 향상 비율입니다.
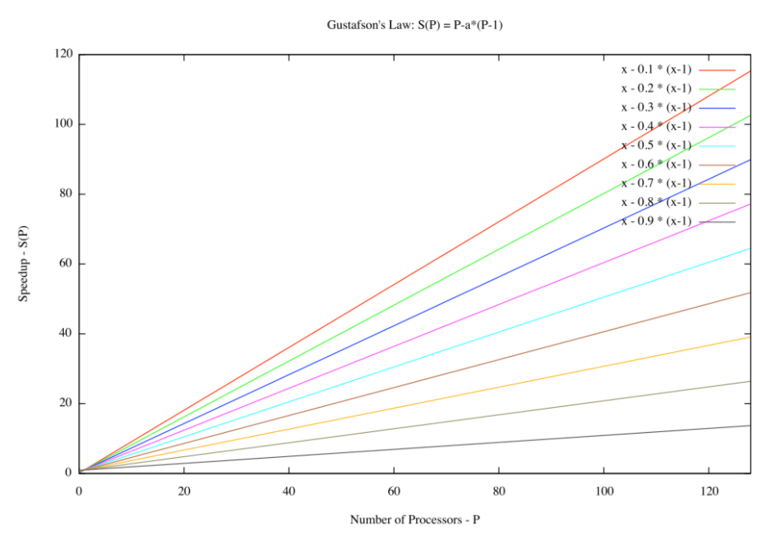
가령 병렬화되지 않는 부분이 전체 프로세스의 50%이고 CPU를 128개 투입한다면 성능 향상은 128 - 0.5 * (128 - 1) = 64.5입니다. 즉 같은 시간 동안 128개의 CPU를 활용해서 64.5배의 데이터를 처리할 수 있게 됩니다.
이렇듯 두 법칙 모두 병렬화되지 않는 부분이 생기는 공통점이 있는데요. 왜 생길까요? 가령 관리자 한명과 근로자들이 있다고 해보겠습니다. 관리자는 근로자들에게 일을 나눠주고 근로자들은 그제서야 일을 시작합니다. 일이 끝나면 관리자에게 보고하고 관리자는 다시 일을 줍니다. 이처럼 관리자가 일을 나눠주고 결과를 모으는 일은 병렬처리가 불가능합니다.
3. Little's Law(리틀의 법칙)
MIT가 개설한 경영과학 과정에서 최초로 학위를 받은 존 리틀에 의해 만들어진 경제와 관련된 법칙으로 프로세스의 안정상태에서의 재고와 산출율 그리고 흐름 시간의 상관관계를 나타낸 법칙. IT에선 성능 평가에 많이 사용됩니다.
n = x * (z + r)
- n = 동시 사용자 수,
- x = 시스템이 처리 가능한 용량(Throughput)
- r = 단위 처리의 응답 시간
- z = 각 단위 처리 사이의 간격(think time)
# 예시 1
이 법칙에 대한 예를 들어보겠습니다. 간단한 성능 테스트를 진행했을 때의 결과가 다음과 같이 나왔다고 하겠습니다. 동시에 1명이 접속하고, think time은 0이고, 꽤 많은 횟수를 테스트하고 평균 응답 시간이 2초로 측정되었다면 이를 리틀의 법칙 수식에 넣으면 다음과 같이 될 것입니다.
1 user = x * (0 sec + 2 sec)
이 수식을 풀면 x 값은 0.5 (user/sec)가 됩니다. 즉, 초당 0.5 사용자의 동시 요청을 처리할 수 있는 용량입니다.
# 예시 2
동일한 시스템에 대하여 더 테스트를 진행합니다. 그래서 다음과 같은 측정값들을 얻었습니다.
동시에 5명이 접속하고, think time은 0 (그리고 당연히 꽤 많은 횟수를 테스트하고) 일 때, 평균 응답 시간이 2.3초가 나왔다면, 다음과 같이 수식이 나올 것입니다.
5 user = x * (0 sec + 2.3 sec)
이 식을 계산하면 x는 대략 2.17 users/sec 의 값을 갖습니다. 즉 일초당 2.17 사용자의 요청(request)를 처리할 수 있습니다.
결과
이런 식으로 계속 동시 사용자를 증가시켜가면서 테스트를 진행합니다. 그리고 throughput에 대한 그래프를 그려가면 어느 순간에 throughput이 이전보다 떨어지는 경우를 발견하게 됩니다. 이 지점이 이 시스템의 최대 성능을 내는 지점이 됩니다. 주로 x 축은 동시 사용자, y 축은 throughput의 형태로 그래프를 그립니다.
잘 구성된 좋은 시스템(하드웨어 + 소프트웨어)는 동시 사용자가 증가해도 응답 시간의 증가율이 낮은 특성을 보입니다.
출처 : https://blog.naver.com/sungjinlee/130020477203
마침
컴퓨터 구조 이번시간에는 유명한 법칙 3가지에 대해 알아봤습니다. 무어의 법칙도 있기는한데 그건 다 알만한 거라서 생략했습니다.
다음시간에는 CPU 성능 측정 방법에 대해 알아보도록 하겠습니다.
References
- 위키피디아 암달의 법칙 : https://ko.wikipedia.org/wiki/%EC%95%94%EB%8B%AC%EC%9D%98_%EB%B2%95%EC%B9%99
- 위키피디아 구스타프슨의 법칙 : https://ko.wikipedia.org/wiki/%EA%B5%AC%EC%8A%A4%ED%83%80%ED%94%84%EC%8A%A8%EC%9D%98_%EB%B2%95%EC%B9%99
- 나무위키 암달의 법칙 : https://namu.wiki/w/%EC%95%94%EB%8B%AC%EC%9D%98%20%EB%B2%95%EC%B9%99
- 리틀의 법칙 - Little's Law : https://blog.naver.com/sungjinlee/130020477203
