백준 11497번 - 통나무 건너뛰기(★★ / O / 1) : Python

기운찬곰·2021년 3월 13일

백준2

목록 보기

3/17

개요

풀이 시간 : 20분
시간 제한 : 1초
메모리 제한 : 256 MB
기출 : ICPC Asia Regional - Daejeon 2015 E번
링크 : https://www.acmicpc.net/problem/11497

문제

남규는 통나무를 세워 놓고 건너뛰기를 좋아한다. 그래서 N개의 통나무를 원형으로 세워 놓고 뛰어놀려고 한다. 남규는 원형으로 인접한 옆 통나무로 건너뛰는데, 이때 각 인접한 통나무의 높이 차가 최소가 되게 하려 한다.

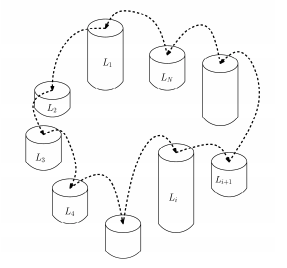
통나무 건너뛰기의 난이도는 인접한 두 통나무 간의 높이의 차의 최댓값으로 결정된다. 높이가 {2, 4, 5, 7, 9}인 통나무들을 세우려 한다고 가정하자. 이를 [2, 9, 7, 4, 5]의 순서로 세웠다면, 가장 첫 통나무와 가장 마지막 통나무 역시 인접해 있다. 즉, 높이가 2인 것과 높이가 5인 것도 서로 인접해 있다. 배열 [2, 9, 7, 4, 5]의 난이도는 |2-9| = 7이다. 우리는 더 나은 배열 [2, 5, 9, 7, 4]를 만들 수 있으며 이 배열의 난이도는 |5-9| = 4이다. 이 배열보다 난이도가 낮은 배열은 만들 수 없으므로 이 배열이 남규가 찾는 답이 된다.

입력

입력은 T개의 테스트 케이스로 이루어져 있다. 첫 줄에 T가 주어진다.

이어지는 각 줄마다 첫 줄에 통나무의 개수를 나타내는 정수 N(5 ≤ N ≤ 10,000), 둘째 줄에 각 통나무의 높이를 나타내는 정수 Li가 주어진다. (1 ≤ Li ≤ 100,000)

출력

각 테스트 케이스마다 한 줄에 주어진 통나무들로 만들 수 있는 최소 난이도를 출력하시오.

해결방법

문제 이해하기

초반에 문제를 읽으면서 이진 탐색인가? 했지만 전체를 다 읽어보니 그렇게 어려운 문제가 아닌거 같았다. 몇분만 잘 생각해보면 쉽게 규칙을 찾을 수 있는 문제.

알고리즘

예를 들어 13 10 12 11 10 11 12 가 있다고 가정해본 다음 생각해보자.

처음에 나는 이렇게 생각했다. 먼저 정렬을 수행한다. 10 10 11 11 12 12 13 이 된다.
그런 다음 순서대로 양쪽 끝에서부터 하나씩 배치를 한다. 이러면 결과적으로 10 11 12 13 12 11 10 이 된다.
그렇게 해서 차이를 구한다음 최대값은 1이 되는 것이다.

그런데 실제로 2번처럼 양쪽 끝에 배치하는거는 할 수는 있겠지만 효율이 떨어질거 같았기 때문에 나는 left, right 배열을 만든다음 하나씩 저장을 번갈아가면서 해주었다.

left : 10 11 12 13
right : 10 11 12

이런 다음 left, right 각 원소마다 차이를 구하고 마지막으로 left 마지막 값과 right 마지막 값도 계산해서 조사를 진행하였다.

더 나은 방법

밑에서 코드를 보겠지만 내 코드는 남들보다 상당히 긴 편이었다. 그래서 다른 사람 코드를 봤더니 더 좋은 방법이 있었다. 굳이 left, right 만들필요없이 i, i + 2 원소끼리 조사를 하면 되었다... (이게 뭔소린지는 코드를 보면 쉽게 이해할 것이다)

Python

내 코드

import sys
input = sys.stdin.readline

if __name__ == "__main__":
    t = int(input())
    for _ in range(t):
        n = int(input())
        data = list(map(int, input().split()))
        data.sort()

        left, right = [], []
        for i in range(n):
            if i % 2 == 0:
                left.append(data[i])
            else:
                right.append(data[i])

        # print(left, right)
        # 1. left간 차이, right간 차이 계산
        # 2. left 마지막과 right 마지막 차이 계산
        result = 0
        for i in range(1, len(left)):
            diff = abs(left[i - 1] - left[i])
            if diff > result:
                result = diff

        for i in range(1, len(right)):
            diff = abs(right[i - 1] - right[i])
            if diff > result:
                result = diff

        print(max(result, abs(left[-1] - right[-1])))