양자 터널링
고전 역학에서는 입자가 에너지 장벽을 넘으려면,
당연히 장벽의 높이보다 더 많은 에너지를 가져야 함.
근데 양자역학에서는 낮은 에너지임에도 일정 확률로 장벽을 터널링해서 넘어간다.
왜냐면 파동 함수에 따라 파동은 에너지 장벽을 확률적으로 통과할 수 있게 됨.
파동 함수: 입자의 양자 상태를 기술. 입자가 주어진 시간과 위치에 가질 수 있는 모든 가능성.
양자 터널링이 문제인 이유
고전 컴퓨터에서 트랜지스터가 나노 크기로 작아지면서, 트랜지스터에서 양자 터널링 현상이 증가하면 전자가 의도하지 않은 방식으로 장벽을 통과하게 된다.
이 경우 누설 전류가 증가하여 전력 소비 증가, 발열, 성능 저하 등 문제를 일으킨다.
게이트
게이트란 일종의 함수이다.
즉, 입력에 따른 출력이 있다.
측정 게이트
측정을 통해 출력이 생기므로 측정도 게이트이다.
중첩 상태의 큐빗을 받아, 0 또는 1을 출력으로 내보낸다.
출력 값은 무작위가 아니라 확률이 존재한다.
(중첩 상태에서 확률이 있음.)
스왑 게이트
2개의 큐빗을 입력받아 상태를 서로 맞바꾼다.
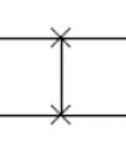
파울리 X 게이트
고전 컴퓨터의 NOT 게이트과 비슷
큐빗을 X축에서 180도 회전
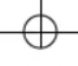
파울리 Y, Z 게이트
1개의 큐빗에 대해 동작
블로그 구의 Y, Z 축을 중심으로 파이 라디안(180도) 회전
즉, 기저 상태의 큐비트가 각각의 게이트를 통과하면 상태가 달라짐.
Y 게이트
|0> 을 i|1>로 매핑
|1>을 -|1>로 매핑
Z 게이트
|0> 은 그대로 둚
|1> 을 -|1>로 매핑
하다마르 게이트(H)
1개의 큐빗에 대해 동작
다음 두 개의 회전 결함
- X축 위에서 파이 만큼
- Y축 위에서 파이/2 만큼
큐비트가 |0> 이면 |0> +|1> / 루트2
큐비트가 |1> 이면 |0> -|1> / 루트2
둘 다 각각 50%이지면, |1> 상태에는 상대적인 위상 차이가 존재
요약: 큐비트를 중첩 상태로 변화시킴
제어 게이트(cX, cY, cZ)
2개 이상의 큐빗에 대해 동작
1개 이상의 큐빗이 연산을 제어 함.
cX: CNOT 게이트
제어 큐빗이 1 상태일 때 타겟 큐빗에 X 게이트(NOT 연산)을 적용
cY
제어 큐빗이 1 상태일 때 타켓 규빗에 Y 연산 적용
(y게이트는 x와 z 게이트 조합과 유사)
cZ
제어 큐빗이 1 상태일 때 타켓 큐빗에 Z 연산을 적용
(z게이트는 큐빗 확률 진폭은 그대로 유지하면서 위상만 변화)
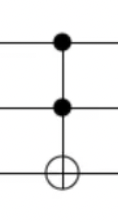
토폴리 게이트(CCNOT)
3개의 큐빗에 대해 동작
처음 2개 큐빗이 1이면 세번 째 큐핏에 X 게이트 적용
그 외에는 변화 없음
|a, b, c> 를 |a, b, c+ab>로 매핑
가역 게이트(출력 값으로 입력 값을 재구축 가능)
양자 게이트의 핵심
중첩 상태를 입력받고 확률값을 회전시켜 또 다른 중첩 상태를 출력값으로 내보낸다.
U 게이트
유니버설 게이트
큐비트 상태에 임의의 단일 큐비트 연산을 적용하게 해줌.
세 가지 회전 각도를 매개변수로 받아 큐비트에 대해 복소수 공간에서의 회전을 정의
큐비트 상태를 조작하기 위해 사용됨.
특정 매개변수를 사용하는게 다른 양자 게이트(파울리 X, Y, Z, H, T 등이 되는 것)
큐빗을 어떻게 만들지?
다양한 방법을 연구 중
이 중 초전로 루프가 가장 앞서 있음.
- 초전도 루프: IMB Q Experience
- 이온 덫
- 실리콘 양자점
- 위상학 큐브
- 다이아몬드 점결합
양자 컴퓨팅이 효과적인 분야
- 복잡한 시뮬레이션
- 분자 모델링과 신소재
- 정교한 딥러닝
- 양자 신경망(QNN)과 인공지능: SF 성격
양자 컴퓨터의 어려움
결 어긋남
양자가 주변 환경과 접촉하면서(관측) 결맞음이 시간의 흐름과 함께 붕괴되는 것
양자 오류
양자 컴퓨팅은 기본적으로 중첩 상태의 큐비트에 게이트를 적용해서, 큐빗을 얽힘으로 만들고 확률을 조작한 후 출력값을 측정함으로써 중첩을 붕괴시켜서 0 또는 1의 시퀀스를 얻는 방식으로 동작함.
그리고 이 모든 계산은 동시에 수행됨. 그리고 계산 결과 우리는 1개의 답을 얻음.
(확률적으로 가장 높은 게 출력)
근데 이 과정에서 오류가 발생할 수도 있음.(확률이니까)
해결 방법의 예시로는 1큐빗의 정보를 9뷰킷의 얽힌 큐빗에 저장해서 오류 정정 코드를 구현
양자 컴퓨터가 특정 종류의 계산 작업에서 고전적 컴퓨터를 능가하는 성능을 보여주는 시점을 지칭
양자 어널링
단열 양자 계산
단열 정리에 의존해 계산을 수행하는 컴퓨팅 방식
제한적 양자 컴퓨팅.
결정적으로 쇼어 알고리즘을 실행할 수 없음.
