CSAPP
운영체제
프로그램은 키보드, 디스플레이, 디스크나, 메인 메모리에 직접 접근하지 않는다.
OS가 제공하는 서비스를 활용한다.
운영체제의 목적
1. 응용프로그램의 하드웨어 오용 방지
2. 응용프로그램이 단순하고 균일한 메커니즘을 사용해 (매우 다른) 저수준 하드웨어 장치 조작 가능하도록
프로세스
프로세스: 실행 중인 프로그램에 대한 운영체제의 추상화
프로세서가 프로세스들을 바꿔주는 방식으로 한 개의 CPU가 다수의 프로세스를 동시에 실행하는 것처럼 보이게 함.
이 때 사용하는 방법이 문맥 전환(context switching)
문맥전환: 현재 프로세스의 컨텍스트를 저장 -> 새 프로세스의 컨텍스트 복원
(제어권을 새 프로세스로 넘겨줌)
OS는 프로세스 실행에 필요한 모든 상태정보를 추적
이러한 상태정보를 컨텍스트라고 함.
컨텍스트의 요소: PC, 레지스터 파일, 메인 메모리의 현재 값을 포함
단일 프로세서는 1개의 프로세스만 실행 가능함!!
동시성(concurrently)이란?
한 프로세스의 인스트럭션들이 다른 프로세스의 인스트럭션들과 섞이는 것
동시성 예시
"shell에 ./hello를 입력하는 상황"
1. 쉘 프로세스 혼자 동작, 입력 대기
2. hello 프로그램 실행 명령
3. 쉘은 시스템 콜(특수 함수)을 호출, OS로 제어권 넘김
4. OS는 쉘의 컨텍스트 저장 -> hello 프로세스 컨텍스트 생성 -> hello 프로세스로 제어권 넘김(context switching)
5. hello가 종료되면 OS를 쉘 프로세스 컨텍스트 복구 -> 쉘 프로세스로 제어권 넘김(context switching)
커널
모든 프로세스를 관리하기 위해 시스템이 이용하는 코드와 자료 구조의 집합
커널은 별도의 프로세스가 아니다.
context switching은 커널에 의해 관리됨.
커널은 OS 코드의 일부분, 메모리에 상주
응용 프로그램 -> OS -> 시스템 콜 -> 커널(제어권) -> 커널(수행) -> 응용 프로그램 리턴
쓰레드(Thread)
프로세스가 다수의 제어 흐름을 가질 수 있음.
해당 프로세스의 컨텍스트에서 동일 코드, 전역 데이터 공유
다수 프로세스보다 다수 쓰레드가 데이터 공유가 더 쉽다
가상 메모리
각 프로세스들이 메인 메모리를 독점하는 것처럼 속이는 추상화
각 프로세스는 가상주소 공간이라는 균일한 메모리를 소유
가상 메모리 영역 구분
-
프로그램 코드 & 데이터
코드: 코드는 모든 프로세스들이 같은 고정 주소에서 시작
데이터: 전역변수에 대응되는 데이터 위치
크기가 고정되어 있다. -
힙(Heap)
런타임 힙
malloc, free로 런타임에서 동적으로 크기가 변함 -
공유 라이브러리
공유 라이브러리의 코드 & 데이터 저장 -
스택
사용자 스택
함수 호출 구현
런타임에서 동적으로 크기 변함
함수 호출 시 크기가 커지며, 리턴 시 작아진다. -
커널 가상메모리
주소공간 맨 위는 커널을 위해 예약됨
응용프로그램이 이 영역 읽기, 쓰기 금지, 커널 영역 내 정의 직접 호출 금지
(단, 커널을 호출하여 위 행위 할 수 있음)
가상 메모리 기본 아이디어
프로세스 가상메모리 내용을 디스크에 저장 -> 메인 메모리를 디스크의 캐시로 사용
파일
단순하게 그냥 연속된 바이트
모든 입출력장치는 파일로 모델링
시스템의 모든 입출력은(유닉스I/O 시스템콜) 파일을 읽고 쓰는 형태
모든 하드웨어는 소프트웨어적인 파일로 모델링된다.
현실에 물리적으로 존재하는 하드웨어를 0과 1의 바이트로 모델링 하는 것이 신기
네트워크
네트워크를 통한 통신도 입출력장치와 통신하는 것과 다르지 않다.
네트워크도 일종의 입출력 장치이다.
telet으로 hello를 실행시키는 예제
1. "hello"를 telet 클라이언트에 입력, 엔터
2. 클라이언트 프로그램이 "hello"를 telnet 서버로 전송
3. teㅣnet 서버는 스트링 받음, 원격 쉘 프로그렘에 전달
4. telnet 서버 -> 네트워크 -> telnet 클라이언트
5.클라이언트 프로그램은 로컬 터미널에 표시 ("Hello, world\n")
Amdahl의 법칙
시스템의 일부분을 개선한 상황에서 성능효과는
1. 전체 시스템 대비 개선한 부분의 중요도
2. 이 부분이 얼마나 빨라졌는지
과 관계 있다.
시스템의 일부분을 개선할 때 전체적으로 얼마나 최대 향상이 있는지 계산
'시스템의 작고 안 중요한 부분 개선하는 것보다 중요하고 큰 부분을 개선해라'는 의미 일까?
암달의 법칙 연습문제 풀어보기
연습문제 1.1
문제 분석
1. 총 거리 2,500km
2. 평균 100km/h
3. 25시간 걸림
4. 거리 중 1,500km에 대하여 150km/h로 주행 가능
5. 속도 개선율은?
풀이
1. 개선하려는 부분의 비율은 1500/2500 = 0.6
2. 개선 효율은 150/100 = 1.5
3. 최종 운행 시간 = (1-0.6)25 + (25*0.6)/1.5
= 25[(1-0.6) + 0.6/1.5]
= 25[0.4 + 0.4]
= 20
4. 속도 개선율 = 25/20 = 1.25
60%에 해당하는 부분을 1.5배 개선했을 때 전체 시스템은 1.25배 개선
연습문제 1.2
문제 분석
1. 목포 개선율 4배
2. 개선 가능 부분 90%
3. 필요한 부분 개선율
풀이
1. 0.25 = (1-0.9) + 0.9/k
2. 0.25 = 0.1 + 0.9/k
3. 0.15 = 0.9/k
4. k0.15 = 0.9
5. k = 0.9/0.15
6. k = 6
90%에 해당하는 부분을 6배 개선 했을 때 전체 시스템은 4배 개선
동시성과 병렬성
동시성: 동시에 일어나는 시스템의 일반적인 개념
병렬성: 동시성을 사용해서 시스템을 빠르게 동작시키는 것
이제 보니 뭔가 이상하다? 2024. 3. 4.
동시성: 한 프로세스가 빠르게 스위칭 하며 동시에 일어나는 것처럼 착각
병렬성: 여러 코어가 물리적으로 병렬적으로 실행
쓰레드 수준 동시성
멀티 프로세서 시스템: 다수의 프로세서가 하나의 OS 커널 제어에 의해 동작
(<-> 유니프로세서)
멀티코어 프로세서: 하나의 프로세서에 여러 CPU(코어) 내장, 별도이 L1, L2 캐시
멀티쓰레딩(하이퍼쓰레딩): 하나의 CPU가 여러 개의 제어 흐름 실행 기술
(멀티쓰레딩) 프로그램 카운터나 레지스터 파일 같은 여러 개의 동일한 CPU 하드웨어를 가지고 있는 반면, 부동소수 연산기와 같은 다른 부분들은 한 개의 하드웨어만 가지고 있는 구조와 관련되어 있다.
무슨 말인지 이해 안 됨
와.. 이제 이해된다. 2024. 3. 4.
파이썬
파이썬의 배열
리스트: mutable(원소 변경 가능) list형 객체
튜플: immutable(원소 변경 불가능)
# 튜플은 결합 연산자 생략 가능
tuple1 = ()
tuple2 = 1,
tuple3 = (1,)
range()
range()함수는 list를 생성하는 게 아니다.
range()는 range객체(연속된 시퀀스를 나타내는 객체)를 생성함.
값을 미리 생성하지 않고 필요한 순간에 생성 -> 효율적인 메모리 관리
순환 가능한 iterable 객체
파이썬 변수 할당 방식
변수 값을 변경하면 값이 복사되는 게 아니라 값을 참조하는 객체 식별 번호가 변경
대입식은 값 자체가 아니라 참조 객체 식별 번호를 대입한다!
배열의 최댓값 구하기
def max_og(arr: list[int]) -> int:
if not arr:
return 0
maximum = arr[0]
for i in range(i, len(arr)):
if arr[i] > maximum:
maximum = arr[i]
return maximum
if name == 'main':
해당 코드가 직접 실행되는지, 임포트 되는지 체크
__name__은 파이썬 내장 변수(built-in variable)
현재 모듈의 이름을 나타냄.
- 스크립트가 직접 실행될 때
__name__은'__main__'이 할당 - 스크립트가 임포트되어 실행될 때
__name__은 원래 모듈 이름
이거 정확히 몰랐는데 확실히 알게 됨!
자료구조
자료구조란?
데이터 단위와 데이터 자체 사이의 물리적 또는 논리적인 관계
-> 데이터가 모여 있는 구조
자료구조를 공부해야 하는 이유?
컴퓨터 데이터를 효율적으로 관리하고 구조화
배열
(C언어 기준으로 공부함)
(파이썬의 리스트는 배열의 유연한 버전? 같은 느낌)
배열: 같은 타입의 변수들로 이루어진 유한 집함
인덱스와 데이터(인덱스에 대응하는)로 이루어진 자료 구조
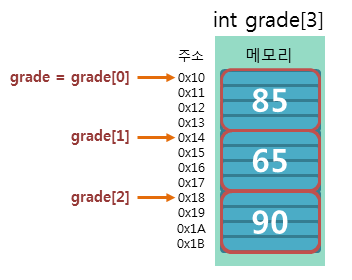
배열이 왜 필요할까?
배열이 없다면 모든 원소에 별도의 변수에 할당해야 한다.
불러올 때도 각 변수를 불러와야 한다.
-> 비효율적이다.
배열의 특징
1. 메모리 상에서 연속된다.
2. 인덱스로 접근할 수 있다.
-> (1&2) 관리가 편하다.
3. 배열의 이름은 배열[0]의 포인터이다.
4. 선언 할 때 배열 크기를 결정하며, 변경할 수 없다.
-> 크기가 부족하거나 낭비되는 문제가 발생한다.
5. 같은 종류 변수만 선언 가능하다.
-> 이를 해결하기 위해 구조체가 등장했다.
문자열
하나 이상의 연속된 문자들의 나열
파이썬에서 문자열은 큰따옴표, 또는 작은따옴표 사이에 위치
# end 매개변수, 기본값: "\n")
print("한 줄 쓰고 ", end="")
print("이어서 쓴다.")print()함수가 자동으로 줄이 바뀌는 이유는
end="\n"이 기본값이기 때문
파이썬 문자열은 배열처럼 순환이 가능하다.
하지만 배열은 아님. 왜냐면 인덱스로 접근해서 수정할 수 없음.
파이썬 문자열은 불변(immutable) 시퀀스 타입
C에서의 문자열
파이썬의 문자열은 <class 'string'> 타입을 갖는다.
그런데 C에는 string이라는 자료형은 없다.
C에서는 char라는 단일 문자 자료형만 있다.
즉, '문자열'을 나타내려면 여러 개의 char를 담을 수 있는 배열을 활용
#include <stdio.h>
int main ()
{
char my_string[] = "Hello";
printf("%s\n", my_string);
return 0;
}C에서 왜
print()가 아니라printf()를 쓸까?
print formatted의 약어이다.
printf는 서식 문자열을 사용하여 서식 지정된 출력(형식화된 방식)을 수행한다.
C의 문자열은 배열이기 때문에 파이썬과 다르게 인덱스로 접근, 삭제, 수정이 가능하다.
#include <stdio.h>
int main ()
{
char my_string[] = "Hello";
my_string[0] = 'N';
printf("%s\n", my_string);
return 0;
}C에서 단일문자는 홑따옴표, 문자열은 쌍따옴표를 쓰는 것에 주의!
복잡도
시간 복잡도
정의: 입력값과 연산 수행 시간의 상관관계를 나타내는 척도
점근 표기법(란다우 표기법: Landau notaion)으로 나타낸다.
(시간 복잡도를 근사치로 표현)
종류
(빠른 순서대로 오름차순)
1. O(1)
2. O(log n)
3. O(n)
4. O(n log n)
5. O(n^2)
6. O(n^3)
7. O(2^n)
8. O(n!)
(log 지수 함수의 역함수이며, 밑이 2다.)
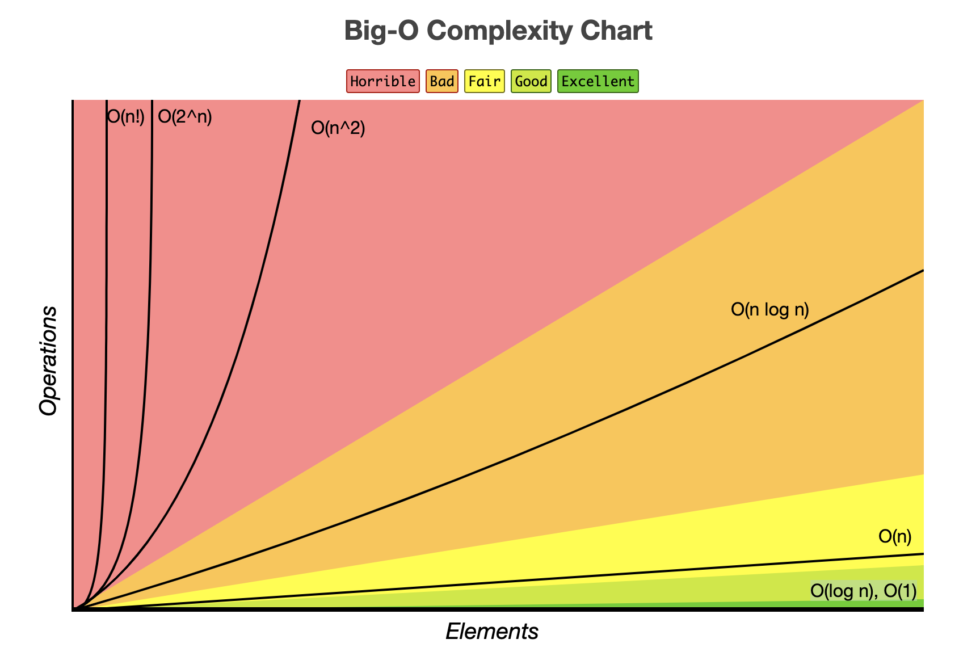
시간 복잡도 표기법
1. Big-O(빅-오) : 상한 점근(최악)
2. Big-Ω(빅-오메가): 하한 점근(최선)
3. Big-θ(빅-세타): 평균(중간)
최악의 경우를 대비하는 게 바람직하다.
시간 복잡도 예시
1. O(1)
constant complexity(일정한 복잡도)
입력 크기와 알고리즘 실행 시간에 선형적인 관계가 없다.
입력값이 증가해도 시간이 늘어나지 않음.(즉시 출력 가능)
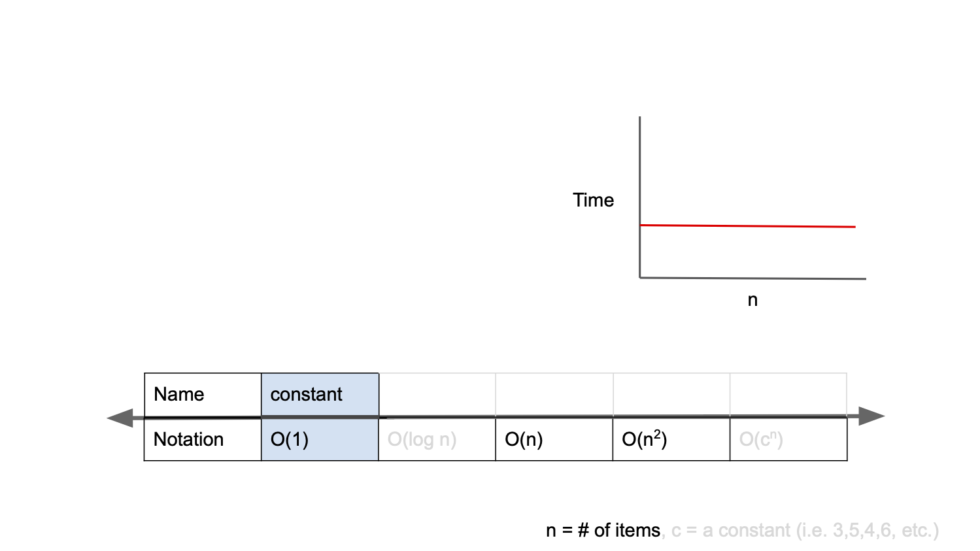
def get_first_element(my_list):
return my_list(0)
my_list = [1, 2, 3, 4, 5]
result = get_first_element(my_list)
print(result)2. O(log n)
logarithmic complexity(로그 복잡도)
절반씩 줄어듦.
대표적으로 이진 검색
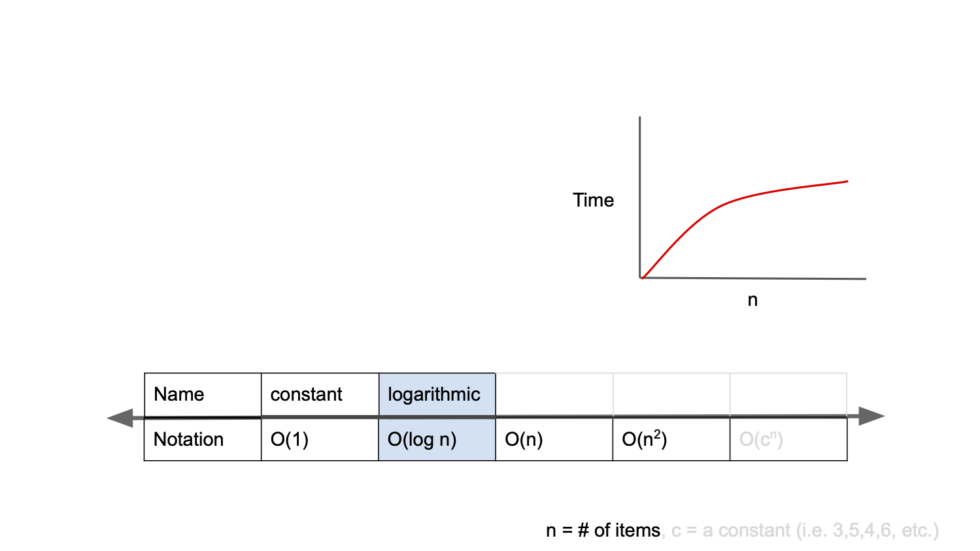
# 단, 이 알고리즘은 이미 정렬된 배열에서 유효함
def binary_search(arr, target):
left, right = 0, len(arr)-1
while left <= right:
mid = (left + right) // 2
if arr(mid) == target:
return mid
elif arr(mid) < target:
left = mid + 1
else:
right = mid - 1
return -13. O(n)
linear complexity(선형 복잡도)
입력 값, 시간이 같은 비율로 증가
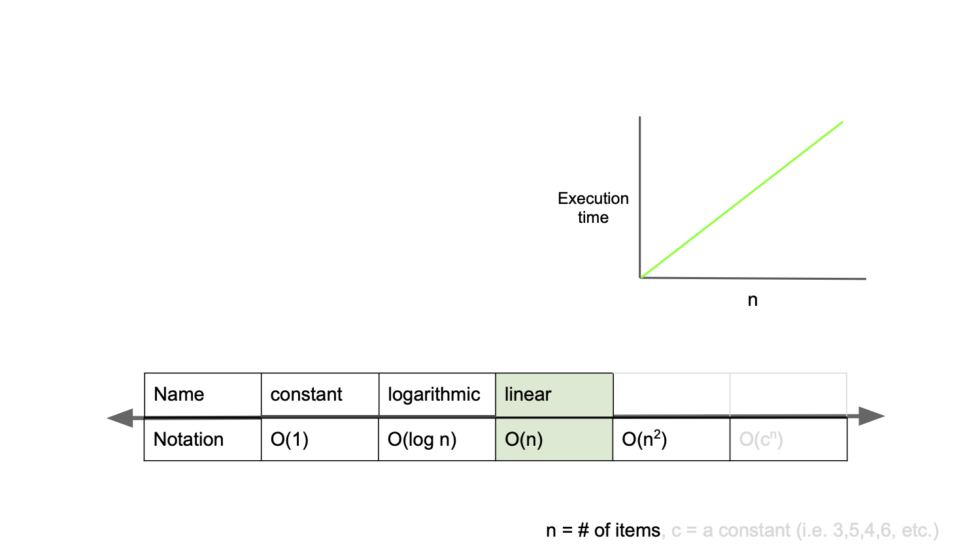
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -14. O(n log n)
대표적으로 병합 정렬
# O(log n)
def merge_sort(arr):
if len(arr) <= 1:
return arr
# 리스트를 반으로 분할
middle = len(arr) // 2
left_half = arr[:middle]
right_half = arr[middle:]
# 각 부분을 재귀적으로 정렬
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)
# 정렬된 각 부분을 병합
return merge(left_half, right_half)
# O(n)
def merge(left, right):
result = []
left_idx, right_idx = 0, 0
while left_idx < len(left) and right_idx < len(right):
if left[left_idx] < right[right_idx]:
result.append(left[left_idx])
left_idx += 1
else:
result.append(right[right_idx])
right_idx += 1
result.extend(left[left_idx:])
result.extend(right[right_idx:])
return result5. O(n^2)
quadratic complexity(2차 복잡도)
입력값의 증가에 따라 시간이 n의 제곱수의 비율로 증가
대표적으로 버블정렬
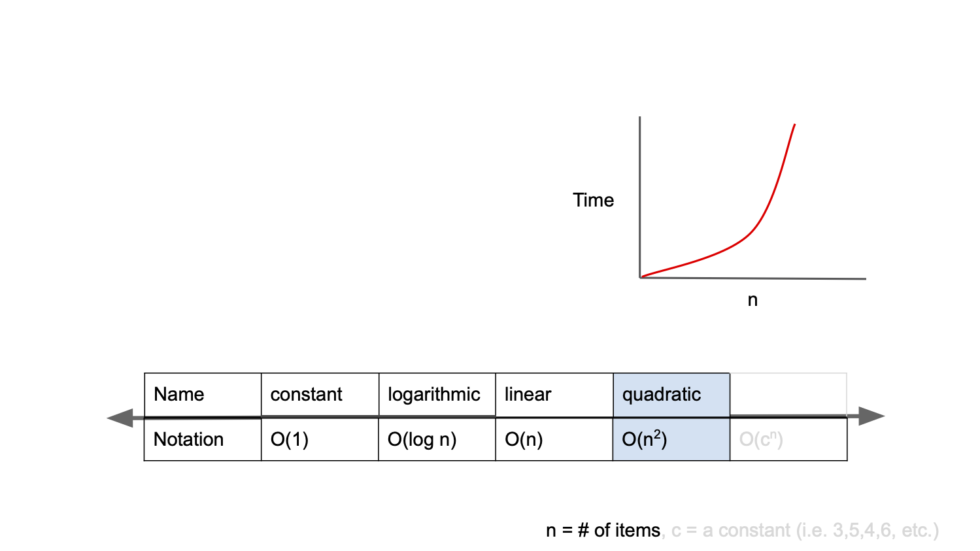
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]6. O(n^3)
def cubic_algorithm(arr):
n = len(arr)
result = 0
for i in range(n):
for j in range(n):
for k in range(n):
result += arr[i] * arr[j] * arr[k]
return result7. O(2^n)
exponential complexity(기하급수적 복잡도)
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)8. O(n!)
def generate_permutations(arr):
if len(arr) == 0:
return [[]]
permutations = []
for i in range(len(arr)):
rest = arr[:i] + arr[i+1:] # i번째 요소 제외
for p in generate_permutations(rest):
permutations.append([arr[i]] + p)
return permutations
def print_permutations(arr):
permutations = generate_permutations(arr)
for p in permutations:
print(p)
my_list = [1, 2, 3]
print_permutations(my_list)공간 복잡도
프로그램 실행 후 완료까지 필요한 자원 공간(메모리)의 양
S(P) = c = Sp(n)
c: 고정 공간(코드 저장 공간, 단순 변수, 고정 크기 구조 변수, 상수)
Sp(n): 가변 공간(동적 공간)
시간 복잡도와 마찬가지로 Big-O로 표현한다.
- O(1): 입력 크기에 상관 없이 고정된 메모리 사용, 변수 1개 선언
- O(log n): 분할 정복, 이진 트리
- O(n): 배열, 리스트
- O(n log n)
- O(n^2): 2차원 배열
- O(N^3): 3차원 배열
- O(2^n): 조합, 부분집합
- O(n!): 가능한 모든 순열 생성
공간 복잡도 예시
1. O(1)
필요한 공간은 i, result, n이 스택에 쌓인다.
즉, n의 값과 무관하게 필요한 공간이 3이므로 O(1)이다.
int factorial(int n)
{
int i = 0;
int result = 1;
for(i = 1; i <= n;, i++)
{
result = result * i;
}
return result;
}2. O(n)
재귀적으로 f(n), f(n-1), f(n-2) ... f(1)까지 스택에 쌓인다.
즉, n의 값만큼 스택영역이 필요하다.
(각 호출 함수마다 필요한 변수는 상수이므로 무시)
int factorial(int n)
{
if(n > 1) return n*factorial(n - 1);
else return 1;
}시간 복잡도와 공간 복잡도는 일반적으로 반비례 관계
현대에는 하드웨어 수준이 높아져 공간 복잡도보다 시간 복잡도를 고려하는 경우가 많다
컴파스 인터뷰 읽어 보고 느낌 점
1. CS기초 지식이 중요하다.(신입, 저연차는 어차피 가르쳐야 한다.)
2. 채용 시 코딩테스트는 과정이다. 정답을 맞추는 게 중요한게 아니라 그 과정을 본다.
3. 일회성 사이드프로젝트, 클론코딩 의미 없다. 실사용 서비스 운영 경험이 중요하다.
정렬
데이터 집합을 일정한 순서 만드는 것
정렬을 왜 해야 할까?
검색이 쉽다!
대표적인 정렬 8가지
1. 버블 정렬
2. 단순 선택 정렬
3. 단순 삽입 정렬
4. 셸 정렬
5. 퀵 정렬
6. 병합 정렬
7. 힙 정렬
8. 도수 정렬
정렬의 핵심은 교환, 선택, 삽입
안정 vs 불안정
안정적인 알고리즘: 같은 값의 원소는 정렬 후 원래 순서 유지 보장
불안정한 알고리즘: 같은 값의 원소는 정렬 후 원래 순서가 보장되지 않음
내부 vs 외부
내부 정렬: 정렬할 모든 데이터를 메모리 상에 모두 로드 가능
외부 정렬: 정렬할 모든 데이터를 메모리 상에 모두 로드 불가능
(외부 정렬은 내부 정렬을 응용한 것, 복잡하다. 외부장치와 연계해야 한다.)
버블 정렬(단순 교환 정렬)
이웃한 두 원소의 대소 관계를 비교하여 필요에 따라 교환을 반복
(교재는 뒤에서부터 교환하는데 앞에서부터 교환하는 걸로 구현해 봄)
import random
def test(fn, count):
for _ in range(count):
origin_arr = [random.randint(1, 100) for _ in range(10)]
sorted_arr = fn(origin_arr)
if sorted_arr == sorted(origin_arr):
print("✅ 테스트에 통과했습니다.")
else:
print("❌ 테스트에 실패했습니다.")
return False
return True
def bubble_sort(arr):
"""버블 정렬"""
n = len(arr)
for i in range(n - 1):
for j in range(1, n - i):
if arr[j - 1] > arr[j]:
arr[j - 1], arr[j] = arr[j], arr[j - 1]
return arr
test(bubble_sort, 1000)버블정렬 원리를 정확히 이해 못해서 처음에는 엉뚱하게 구현했음.
버블 정렬은 바깥 반복이 끝나면 다시 처음부터 비교 해야 하는데,
1회전 시 두 포인터를 모두 하나씩 이동하는 형태로 착각함.
그래서 테스트 코드를 짜 보았음!
버블 정렬의 시간 복잡도는?
O(n^2)
버블 정렬의 공간 복잡도는?
O(1): 입력 배열 외 별도의 메모리 공간 필요하지 않음
버블 정렬 알고리즘의 개선1
핵심 아이디어: 만약 한 사이클을 돌 때 한번도 교환이 이루어지지 않으면 이미 정렬된 배열이라는 뜻이므로 즉시 코드을 종료한다.
import random
def test(fn, count):
for _ in range(count):
origin_arr = [random.randint(1, 100) for _ in range(10)]
sorted_arr = fn(origin_arr)
if sorted_arr == sorted(origin_arr):
print("✅ 테스트에 통과했습니다.")
else:
print("❌ 테스트에 실패했습니다.")
return False
return True
def bubble_sort(arr):
"""버블 정렬"""
n = len(arr)
for i in range(n - 1):
exchage = 0
for j in range(1, n - i):
if arr[j - 1] > arr[j]:
arr[j - 1], arr[j] = arr[j], arr[j - 1]
exchage += 1
if exchage == 0:
break
return arr
test(bubble_sort, 100)버블 정렬 알고리즘 개선 2
핵심 아이디어: 특정 원소 이후에 교환이 이루어지지 않으면 부분 정렬로 간주하고 그 부분은 정렬하지 않는다.
# 작성 중
