정렬(어제 이어서)
단순 선택 정렬(Straight selection sort)
가장 작은 원소부터 선택해 알맞은 위치로 옮기는 작업을 반복
기본 아이디어: 정렬이 되지 않은 나머지 부분의 전체를 훑으면서 가장 작은 원소를 나머지 중 가장 앞과 교환함
요약: 제일 작은 애를 기억해서 (정렬이 아직 안 된 부분의) 맨 앞으로 보낸다!
불안정한 알고리즘(기존 순서 보장 안됨)
시간 복잡도는 O(n^2)
import random
def test(fn, count):
for _ in range(count):
origin_arr = [random.randint(1, 100) for _ in range(10)]
sorted_arr = fn(origin_arr)
if sorted_arr == sorted(origin_arr):
print("✅ 테스트에 통과했습니다.")
else:
print("❌ 테스트에 실패했습니다.")
print(origin_arr)
print(sorted_arr)
return False
return True
def selection_sort(arr):
"""단순 선택 정렬"""
n = len(arr)
for i in range(n - 1):
min = i
for j in range(i + 1, n):
if arr[j] < arr[min]:
min = j
arr[i], arr[min] = arr[min], arr[i]
return arr
test(selection_sort, 100)단순 삽입 정렬(straight insertion sort)
(셔틀 정렬(shuttle sort)
주목한 원소보다 더 앞쪽에서 알맞은 위치로 삽입
기본 아이디어:
(1) 현재 포인터의 원소를 임시 공간에 저장
(2) 현재 포인터 바로 직전 원소와 비교
(2-1) 직전 원소가 더 크면 현재 원소 값에 직전 원소 값을 덮어씌움 > 반복
(임시 공간에 저장된 원소가 알맞은 위치를 찾아가는 과정)
(2-2) 직전 원소가 더 작으면 이미 정렬이 완료되었으므로 임시 공간의 값을 직전 원소 값에 임시 공간 원소 값을 덮어 씌움(사실상 교환 효과)
시간 복잡도는 O(n^2)
안정 알고리즘(기존 순서 보장됨)
단순 선택 정렬과 다른 점은?
가장 작은 원소를 선택하지 않는다!
요약: 이미 정렬된 부분을 유지하면서 새로운 원소를 이미 정렬된 부분에 삽입한다.
삽입을 위해 비교를 할 때마다 직전 원소를 다음 원소로 복사한다.
import random
def test(fn, count):
for _ in range(count):
origin_arr = [random.randint(1, 100) for _ in range(10)]
sorted_arr = fn(origin_arr)
if sorted_arr == sorted(origin_arr):
print("✅ 테스트에 통과했습니다.")
else:
print("❌ 테스트에 실패했습니다.")
print(origin_arr)
print(sorted_arr)
return False
return True
def insertion_sort(arr):
"""단순 삽입 정렬"""
n = len(arr)
for i in range(1, n):
j = i
current_element = arr[i]
while j > 0 and arr[j - 1] > current_element:
arr[j] = arr[j - 1]
j -= 1
arr[j] = current_element
return arr
test(insertion_sort, 100)
이해는 했음! 코드 직접 짜보자!
교재에 tmp라고 명명한 곳은 이해가 어렵다.
현재 체크 대상이 되는 숫자니까, now_number, checking_number, current_element 같은 변수명이 더 가독성 있을 것 같다!
단순 삽입 정렬은 n이 커지면 비교/교환 비용이 커진다.
이진 삽입 정렬(binary insertion sort)로 해결할 수 있다.
(이건 전체 정렬 훑어보고 심화 학습해보기)
셸 정렬(shell sort)
단순 삽입 정렬의 장점 살리고, 단점 보완
단순 삽입 정렬은 삽입할 위치가 멀리 떨어져있으면 성능이 안 좋다.
그래서 그룹을 나누어서 삽입할 위치를 가깝게 만들어 주는 것이 셸 정렬
(이름에 의미가 있는 건 아니고 '도널드 셸'이 고안한 알고리즘)
불안정한 정렬(기존 순서가 보장되지 않는다.)
정렬 횟수는 늘어나지만 원소의 이동 횟수가 줄어들어 효율적이다.
셸 정렬을 수행할 때는 h-정렬을 여러 번 수행한다.
h-정렬: h칸 떨어져 있는 2개의 원소를 정렬
기본 아이디어
1. h-정렬을 통해 거의 정렬된 배열을 만든다.
2. 마지막으로 단순 삽입 정렬을 1회 수행한다.(1-정렬과 동일)
효율적인 h값
1. h는 서로 배수가 되면 안 된다.
2. 효율적인 h값: h = h * 3 + 1
(h는 h를 9로 나누었을 때 몫을 넘으면 안 된다.)
어려워서 보류퀵 정렬(quick sort)
가장 빠른 정렬, 널리 사용됨
핵심 아이디어: 피벗을 기준으로 작은 건 왼쪽으로 몰고, 큰건 오른쪽으로 몬다.
피봇 + 파티셔닝
1. 스왑하는 방법
import random
def test(fn, count):
for _ in range(count):
origin_arr = [random.randint(1, 100) for _ in range(10)]
answer = sorted(origin_arr)
sorted_arr = fn(origin_arr, 0, len(origin_arr) - 1)
if origin_arr == answer:
print("✅ 테스트에 통과했습니다.")
else:
print("❌ 테스트에 실패했습니다.")
print(origin_arr)
print(answer)
return False
return True
def quick_sort(arr, start, end):
"""퀵 정렬"""
if start >= end:
return arr
pivot = start
left_pt = start + 1
right_pt = end
while left_pt <= right_pt:
while left_pt <= end and arr[left_pt] <= arr[pivot]:
left_pt += 1
while right_pt > start and arr[right_pt] >= arr[pivot]:
right_pt -= 1
# 이 순간에 잘못된 원소 2개를 각각의 파티션에서 찾은 것
# arr[left_pt]와 arr[right_pt]는 바뀌어야 한다.
if left_pt > right_pt:
arr[right_pt], arr[pivot] = arr[pivot], arr[right_pt]
else:
arr[left_pt], arr[right_pt] = arr[right_pt], arr[left_pt]
quick_sort(arr, start, right_pt - 1)
quick_sort(arr, right_pt + 1, end)
test(quick_sort, 1000)
2. 별도의 배열을 만들고 합치는 방법
import random
def test(fn, count):
for _ in range(count):
origin_arr = [random.randint(1, 100) for _ in range(10)]
sorted_arr = fn(origin_arr)
if sorted_arr == sorted(origin_arr):
print("✅ 테스트에 통과했습니다.")
else:
print("❌ 테스트에 실패했습니다.")
return False
return True
def quick_sort(arr):
"""퀵 정렬"""
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
lesser_arr, equal_arr, greater_arr = [], [], []
for num in arr:
if num < pivot:
lesser_arr.append(num)
elif num > pivot:
greater_arr.append(num)
else:
equal_arr.append(num)
return quick_sort(lesser_arr) + equal_arr + (quick_sort(greater_arr))
test(quick_sort, 1000)
퀵 소트 아이디어는 이해했음!
아직 퀵 소트 혼자 코드 못 짜겠음ㅠ 우선 넘어간다!
알고리즘
파이썬 문법 추가
set 객체
set 객체는 인덱스로 접근할 수 없다! (순서를 보장하지 않는다.)
sort에 lambda 적용
N = int(input())
words = []
for _ in range(N):
word = input()
words.append(word)
words = list(set(words))
sorted_arr = sorted(words, key=lambda x: (len(x), x))
for word in sorted_arr:
print(word)
lambda 함수란?
익명 함수(Anonymous Function)
주로 한 줄로 간단한 연산을 수행할 때 사용
# 기본 문법
lambda aarguments: expression(return value)
# 간단한 예시
add = lambda x, y: x + y
result add(3, 5)
# 정렬 예시
data = [(1, 'apple'), (3, 'banana'), (2, 'cherry')]
data.sort(key=lambda x: x[1]) # 두 번째 요소를 기준으로 정렬람다 함수(+ filter)를 연습해 보자!
# 주어진 수 중에서 짝수만 필터링 하기
numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
even_numbers = list(finter(lambda x: x % 2 == 0, numbers))
# filter 사용법
filter(function, iterable)분할 정복((Divide and Conquer)
특정한 알고리즘이 아니라 알고리즘 설계의 패러다임
분할 정복의 사례
병합 정렬, 퀵소트
이진 검색
거듭제곱 계산
그래픽 문제
행렬 곱셉
재귀 함수
거듭제곱 계산을 분할 정복으로
# 반복문으로 풀기
def pow(x, n):
answer = 1
for _ in range(n):
answer = answer * x
return answer
# 분할 정복으로 풀기
def power(x, n):
if n == 0:
return 1
half_pow = power(x, n // 2)
elif n % 2 == 0:
return half_pow * half_pow
else:
return x * half_pow * half_pow재귀가 모두 분할 정복이 아니다.
분할 정복 안에 재귀가 일부분 들어가 있는 개념
재귀지만 분할 정복은 아닌 예
def power(x, n):
if n == 0:
return 1
else:
return x * power(x, n - 1)재귀를 좀더 자세히 알아 보았다.
def power(x, n):
print(f"x: {x} / n: {n} 함수를 호출합니다.")
if n == 0:
print(f"[리턴] 1")
return 1
else:
result = x * power(x, n - 1)
print(f"[리턴] {result}")
return result
print(power(2, 10))
x: 2 / n: 10 함수를 호출합니다.
x: 2 / n: 9 함수를 호출합니다.
x: 2 / n: 8 함수를 호출합니다.
x: 2 / n: 7 함수를 호출합니다.
x: 2 / n: 6 함수를 호출합니다.
x: 2 / n: 5 함수를 호출합니다.
x: 2 / n: 4 함수를 호출합니다.
x: 2 / n: 3 함수를 호출합니다.
x: 2 / n: 2 함수를 호출합니다.
x: 2 / n: 1 함수를 호출합니다.
x: 2 / n: 0 함수를 호출합니다.
[리턴] 1
[리턴] 2
[리턴] 4
[리턴] 8
[리턴] 16
[리턴] 32
[리턴] 64
[리턴] 128
[리턴] 256
[리턴] 512
[리턴] 1024
1024재귀는 계속해서 함수가 호출됐다가, 베이스 조건일 때 호출됐던 함수가 거꾸로 리턴된다. 함수 호출 스택(Function Call Stack)에서 쌓이다가 꺼내온다. 그래서 재귀가 너무 깊으면 콜 스택이 넘쳐 버릴 수도 있다.
이럴 때를 '스택 오버플로우'라고 한다!!
1부터 10까지 구하는 걸 분할정복으로 풀어봤음!
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
def summary(arr):
length = len(arr)
mid = length // 2
if length == 1:
print(arr[0])
return arr[0]
print(arr[0:mid], arr[mid:])
return summary(arr[0:mid]) + summary(arr[mid:])
print(summary(arr))
[1, 2, 3, 4, 5] [6, 7, 8, 9, 10]
[1, 2] [3, 4, 5]
[1] [2]
1
2
[3] [4, 5]
3
[4] [5]
4
5
[6, 7] [8, 9, 10]
[6] [7]
6
7
[8] [9, 10]
8
[9] [10]
9
10
55base와 recursive를 정하고 푸니까 풀림.
근데 아직까지 어떤 과정으로 풀어지는지 잘 모르겠음.
어쨌든 분할 정복과 재귀에 대해서 감은 잡긴 함.
백준 1629 나머지 분배 법칙
분할 정복(재귀)로 풀었는데 나머지 분배 법칙 못해서 인터넷 찾아봄
나머지 분배 법칙
(a + b) % m = ((a % m) + (b % m)) % m
(a - b) % m = ((a % m) - (b % m) + m) % m
(a * b) % m = ((a % m) * (b % m)) % m
나머지 분배 법칙을 통해 정수 오버플로우를 방지할 수 있다!
화요일 퀴즈 준비
자료구조
배열(정적, 동적)
스택(FILO)
큐(FIFO)
해쉬
링크드리스트(단일, 이중)
정렬 종류
1. 버블 정렬
2. 단순 선택 정렬
3. 단순 삽입 정렬
4. 셸 정렬
5. 퀵 정렬
6. 병합 정렬
7. 힙 정렬
8. 도수 정렬
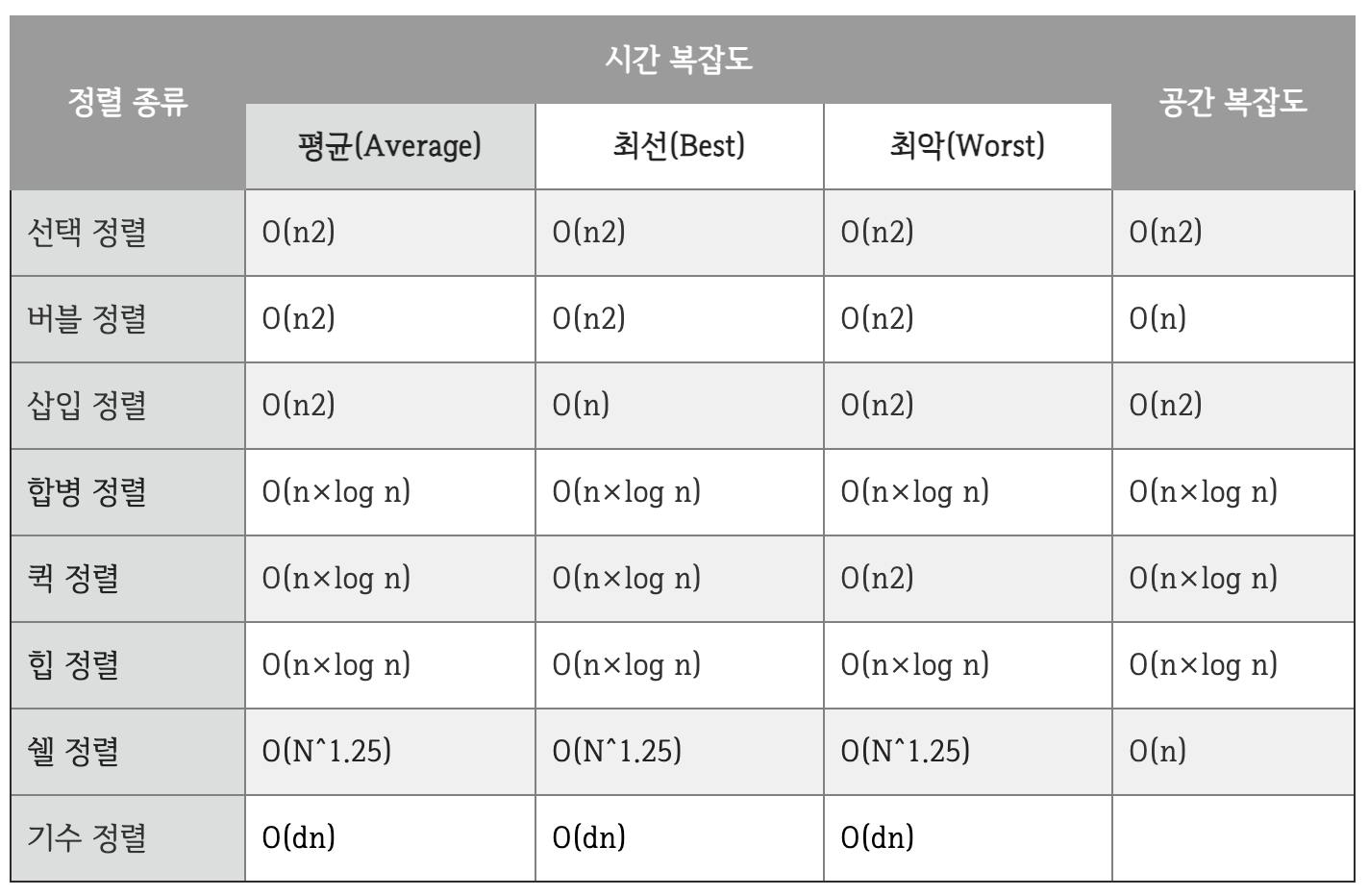
정렬별 시간 복잡도
삽입 정렬 O(n^2)
퀵 소트 O(n^2) 평균 n log n (왜 퀵 소트를 선호?)
머지(병합) 소트 O(n log n)
힙 소트 O(n log n)
선택 정렬 O(n^2)
버블 정렬 O(n^2)
쉘 정렬 O(n^2)
안정한 정렬 vs 불안정 정렬
안정한 정렬: 중복된 값을 입력 순서와 동일하게 한다.
(버블, 삽입, 쉘, 병합)
불안정한 정렬: 중복된 값의 입력 순서가 보장되지 않는 것.
(선택, 퀵, 힙, 도수)
n개의 정렬의 최대 성능은 O(n lon n) 증명이 됨.
(머지나 퀵보다 더 빠르게 짤 수 없다.)
검색(탐색)
검색의 종류
1. 선형 검색(완전 탐색)
2. 이진 검색
3. 해시법
선형 검색(완전 탐색, linear search)
찾을 때까지 맨 앞에서부터 검색
선형 검색 종료 조건
1. 값이 없음(맨 끝을 지남)
2. 값이 있음(검색 성공)
시간 복잡도
운이 좋으면 O(1), 운이 나쁘면 O(n)
보초법(sentinel method)
sentinel: 정보 요소의 시작, 또는 끝을 마크하는 기호
(보초병, 보호자 역할을 함)
보초법의 핵심 아이디어
선형 검색에서는 매 원소 검색 시마다 종료 조건 2가지를 탐색해야 한다.
이 때 매번 2번씩 조건을 확인하는 건 비용이 증가한다.
그래서 기존 배열의 마지막에 보초(찾으려는 값)을 추가해서,
매 탐색마다 '원소가 있는지'만 체크하고, '배열이 끝났는지'는 체크하지 않는다.
arr = [3, 1, 6, 4, 8, 9, 0, 5, 6, 7, 3, 4, 1, 2]
target = 1
def linear_search(arr, target):
temp = arr[:]
bocho_index = len(arr)
temp.append(target)
i = 0
while True:
if temp[i] == target:
break
i += 1
return -1 if i == bocho_index else 1
print(linear_search(arr, target))
이진 검색(binary search)
중요! 이진 검색을 하려면 데이터가 정렬되어 있어야 한다.
이진 검색은 선형 검색보다 빠르다.
백준 1920 이진 탐색에서 없는 경우 0을 출력해야 하는 -1을 출력해서 계속 삽질함. 문제 제대로 읽자!
삽질해서 구현한 이진 검색 코드 원본
N = int(input())
arr = list(map(int, input().split()))
arr.sort()
M = int(input())
targets = list(map(int, input().split()))
for target in targets:
left_pointer = 0
right_pointer = len(arr) - 1
while True:
mid = (left_pointer + right_pointer) // 2
if target == arr[mid]:
print(1)
break
elif target < arr[mid]:
right_pointer = mid - 1
else:
left_pointer = mid + 1
if left_pointer > right_pointer:
print(0)
breakwhile문 조건을 개선
N = int(input())
arr = list(map(int, input().split()))
arr.sort()
M = int(input())
targets = list(map(int, input().split()))
for target in targets:
left_pointer = 0
right_pointer = len(arr) - 1
found = False
while left_pointer <= right_pointer:
mid = (left_pointer + right_pointer) // 2
if target == arr[mid]:
found = True
break
elif target < arr[mid]:
right_pointer = mid - 1
else:
left_pointer = mid + 1
if found:
print(1)
else:
print(0)이진 검색도 재귀로 풀어보자!
김코치님이 알려주신 브랜치 사이트 퀴즈 끝나고 연습
https://learngitbranching.js.org/?locale=ko
자료구조
(배열은 어제 했음)
(참고로 파이썬의 리스트는 배열과 유사하지만 배열은 아님. 동적 배열 또는 유사 배열이라고 할 수 있음.)
스택
스택은 데이터를 임시 저장할 때 사용하는 자료 구조
후입선출(LIFO, Last In First Out)
push: 스택에 데이터 넣기
pop: 스택에서 데이터 꺼내기
top: 스택의 맨 위
bottom: 스택의 맨 아래
스택 배열(stk): skt[0] = 스택의 bottom
스택 크기(capacity): 스택의 최대 크기를 나타내는 정수
스택포인터(prt): 스택에 쌓여 있는 데이터의 정숫값
(스택이 비어있으면 포인터는 0, 가득 차면 포인터는 capacity)
파이썬 스택 Hands On
스택에서 사용할 수 있는 다양한 메서드를 직접 구현해야 함.
from typing import Any
import random
class FixedStack:
"""고정 길이 클래스"""
class Empty(Exception):
"""비어 있는 FixedStack에 팝 또는 피크할 때 내보내는 예외 처리"""
def __init__(self, message="스택이 비었습니다."):
self.message = message
super().__init__(self.message)
class Full(Exception):
"""가득 찬 FixedStack에 푸시할 때 내보내는 예외 처리"""
def __init__(self, message="스택이 가득 찼습니다."):
self.message = message
super().__init__(self.message)
def __init__(self, capacity: int = 256) -> None:
"""스택 초기화"""
self.stk = [None] * capacity # 스택 본체
self.capacity = capacity # 스택의 크기
self.ptr = 0 # 스택 포인터
def __len__(self) -> int:
"""스택에 쌓여 있는 데이터 개수를 반환"""
return self.ptr
def is_empty(self) -> bool:
"""스택이 비어 있는지 판단"""
return self.ptr <= 0
def is_full(self) -> bool:
"""스택이 가득 차 있는지 판단"""
return self.ptr >= self.capacity
def push(self, value: Any) -> None:
"""스택에 value를 푸시"""
if self.is_full():
raise FixedStack.Full
self.stk[self.ptr] = value
self.ptr += 1
def pop(self) -> Any:
"""스택에서 데이터를 팝"""
if self.is_empty():
raise FixedStack.Empty
self.ptr -= 1
return self.stk[self.ptr]
def peek(self) -> Any:
"""스택에서 데이터를 피크"""
if self.is_empty():
raise FixedStack.Empty
return self.stk[self.ptr - 1]
def clear(self) -> None:
"""스택을 비움(모든 데이터 삭제)"""
self.ptr = 0
def find(self, value: Any) -> Any:
"""스택에서 value를 찾아 인덱스를 반환(없으면 -1을 반환)"""
for i in range(self.ptr - 1, -1, -1):
if self.stk[i] == value:
return i # 검색 성공
return -1 # 검색 실패
def count(self, value: Any) -> int:
"""스택에 있는 value의 개수를 반환"""
c = 0
for i in range(self.ptr): # 바닥 쪽부터 선형 검색
if self.stk[i] == value: # 검색 성공
c += 1
return c
def __contains__(self, value: Any) -> bool:
"""스택에 value가 있는지 판단"""
return self.count(value) > 0
def dump(self) -> None:
"""덤프(스택 안의 모든 데이터를 바닥부터 꼭대기 순으로 출력)"""
if self.is_empty(): # 스택이 비어있음
print('스택이 비어 있습니다.')
else:
print(self.stk[:self.ptr])
# 스택 생성
stack = FixedStack(64)
# 더미 데이터 생성
random_num = [random.randint(1, 100) for _ in range(100)]
# 더미 데이터 push
for n in random_num:
stack.push(n)
# 데이터 개수
print("스택에 들어있는 데이터 개수")
print(len(stack))
# 팝
print("pop")
print(stack.pop())
# 커패시티(스택 크기)
print("capacity")
print(stack.capacity)
# 포인터
print("현재 포인터")
print(stack.ptr)
# 검색
print("10을 검색")
print(stack.find(10))
# 개수 카운트
print("7이 몇 개인지 카운트")
print(stack.find(7))
# 덤프
print("dump")
stack.dump()
# 픽(엿보기)
print("peek")
print(stack.peek())
# 스택 비우기
print("clear")
stack.clear()
# 스택 길이(비우기 확인)
print("len")
print(len(stack))
__len__(self)로 지정하는 이유
이렇게 하면 파이썬 내장 함수 len()과 연결되어
stack.__len__()를len(stack)으로 쓸 수 있음.
스택을 비울 때 포인터를 0으로 하는 방식은 메모리 누수가 발생하지 않을까?
맞음. 하지만 파이썬 같은 건 알아서 가비지 컬렉션 내장.
그리고 포인터를 초기화 하는 방식으로 스택을 비우면, 새로운 데이터가 스택에 push될 때 덮어쓰기가 되기 때문에 문제는 없음!
스택을 직접 구현해 봤다! 교재 보고 따라친거지만 hands-on에 의미!
스택의 구조와 메서드가 확실히 이해되었음!
파이썬의 Exception 클래스
Exception은 모든 내장 예외의 기본 클래스
Exception 클래스를 통해 많은 예외 처리를 쉽게 사용할 수 있음
class CustomError(Exception):
passclass에 단지 Exception클래스를 상속받기만 해도 사용자 정의 예외를 사용할 수 있음!
여기에__init__으로 기본 메시지 지정하면 에러 발생 시 커스텀 메시지 출력할 수도 있음!
