07:50 입실
어제 모기 한 마리가 계속 시끄럽게해서 잠을 잘 못 잠.
잠깐 깼는데 뭔가 개발하거나(또는 알고리즘 풀기) 꿈을 꿨음
아침에 일어났는데 왼쪽 어깨 근육이 아픔. 스트레칭 자주 하기.
백준 18352: 특정 거리의 도시 찾기(다익스트라)
문제 보고 다익스트라 떠오름.
근데 BFS가 훨신 간단하다고 하는데 다익스트라 연습할 겸 다익스트라로 풀어봄.
(근데 다익스트라 혼자 100% 제대로 구현 못함. 우선 더듬더듬 코딩함.)
# 출발도시 X 노드에 대한 각 노드들의 최단거리를 구하는 것(다익스트라)
import sys
from collections import defaultdict
import heapq
def dijkstra(graph: defaultdict, node_count: int, start_node: int) -> list:
INF = float("inf")
# 노드별 최단거리 초기화
distances = [INF] * (node_count + 1)
# 힙(우선순위 큐) 생성
queue = []
# 힙에 최초 노드 삽입(가중치 0)
distances[start_node] = 0
heapq.heappush(queue, (0, start_node))
while queue:
distance, current_node = heapq.heappop(queue)
if distances[current_node] < distance:
continue
for adj_distance, adj_node in graph[current_node]:
new_distance = distance + adj_distance
if new_distance < distances[adj_node]:
distances[adj_node] = new_distance
heapq.heappush(queue, (new_distance, adj_node))
return distances
N, M, K, X = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
graph = defaultdict(list)
for edge in edges:
u, v = edge
graph[u].append((1, v))
distances = dijkstra(graph, N, X)
result = []
for i in range(1, N + 1):
if distances[i] == K:
result.append(i)
if result:
result.sort()
for node in result:
print(node)
else:
print(-1)70% 정도는 혼자 힘으로 구현한 듯
오류가 많아서 GPT 도움 받았지만 기본적인 틀은 혼자 구현함!
오류 복기
문제 제대로 안 읽음.
출발 지점이 X인데 무조건 1부터 시작함.
해당하는 거리가 없으면 -1을 출력해야 하는데 빼먹음.
오름차순으로 출력해야하는데 그냥 출력함.
시작 노드 거리를 0으로 초기화하지 않아서 계속 틀림
백준 18352: 특정 거리의 도시 찾기(BFS)
BFS로도 풀어봄
from collections import defaultdict, deque
import sys
N, M, K, X = map(int, input().split())
graph = defaultdict(list)
for _ in range(M):
u, v = map(int, sys.stdin.readline().split())
graph[u].append(v)
distances = [-1] * (N + 1)
distances[X] = 0
queue = deque([X])
while queue:
current_node = queue.popleft()
for next_node in graph[current_node]:
if distances[next_node] == -1:
distances[next_node] = distances[current_node] + 1
queue.append(next_node)
result = [i for i, d in enumerate(distances) if d == K]
if result:
for node in result:
print(node)
else:
print(-1)BFS는 너비 우선 탐색이니까 처음 방문한 곳을 다시 방문할 필요가 없음.
왜냐면 이미 방문한 곳을 나중에 다시 방문하는 순간 그건 최단거리가 아님.
(이때는 각 노드들 간의 거리가 동일하다는 전제)
만약 거리 간에 가중치가 있다면, 다익스트라로 가야 함.
백준 11725 트리의 부모 찾기
80% 정도 혼자 풂! 전체적인 아이디어는 맞았는데 DFS 재귀를 아직 확실하게 이해하지 못한 듯.
# 트리의 부모 찾기
import sys
from collections import defaultdict
sys.setrecursionlimit(10 ** 6)
def dfs(tree, node, N, parents=None, visited=None):
if parents is None:
parents = [i for i in range(N + 1)]
if visited is None:
visited = set()
visited.add(node)
for adj_node in tree[node]:
if adj_node not in visited:
parents[adj_node] = node
dfs(tree, adj_node, N, parents, visited)
return parents
N = int(sys.stdin.readline().strip())
edges = []
while True:
try:
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
except:
break
tree = defaultdict(list)
for edge in edges:
u, v = edge
tree[u].append(v)
tree[v].append(u)
result = dfs(tree, 1, N)
for node in result[2:]:
print(node)재귀 쓸 때는 백준에서 무조건 리커전 리밋 풀기!
디폴트 인자로 변경 가능한 타입을 사용하는 것을 피하기! (안티 패턴)
함수 내에서 변경한 값이 함수 밖에 영향을 미칠 수 있어서 예기치 않은 동작을 할 수 있다.
Do not use mutable default arguments in Python, unless you have a REALLY good reason to do so.
Instead, default to None and assign the mutable value inside the function
https://florimond.dev/en/posts/2018/08/python-mutable-defaults-are-the-source-of-all-evil/
백트래킹(Backtracking)
해결책에 대한 후보를 구축하다가 가능성이 없다고 판단되는 즉시 후보를 포기(백트랙)
브루트포스는 가능성 여부와 무관하게 모두 다 탐색하지만
DFS를 통하 백트래킹은 가능성이 없으면 추가 탐색을 진행하지 않는다.
DFS로 순열 구현하기
def permute(data, depth, n, r, result=None):
if result is None:
result = []
if depth == r:
result.append(tuple(data[:r]))
return
for i in range(depth, n):
data[depth], data[i] = data[i], data[depth]
permute(data, depth + 1, n, r, result)
data[depth], data[i] = data[i], data[depth]
return result
data = [1, 2, 3]
result = permute(data, 0, len(data), len(data))
print(result)
이거 진짜 하루 종일 고민했음.
(오전 8시부터 오후 7시까지 고민함)
depth랑 i 왜 스왑하는거야!!!!!!!
GPT계속 물어봐서 알아냈음.
depth까지 이미 확정됐다고 생각한 게 문제
dpeth는 확정된 자리가 아니라, depth이전까지 확정된 것.
depth는 유동적인 공간으로, depth를 포함해서 그 뒤에 요소를 하나씩 집어넣고,
나머지 뒷부분을 재귀로 돌리는 것!
아직 재귀적 사고에 100% 적응하지 못해서 100% 이해는 아니지만,
지금까지 이해했던 재귀 함수에 비추어 볼 때 흐름은 이해함.
퀴즈 후기
- 다익스크라 이해하려고 열심히 노력한 보람이 있음. 실행 흐름에 맞게 잘 적어서 냄.
- DFS, BFS 수도 코드 구현. 여러번 연습한 보람이 있음. 스택과 큐로 어떻게 탐색이 이루어지는지 확실히 설명할 수 있음.
- 프로세스, 쓰레드 : 실행 컨텍스트라는 용어를 오용함. 컨텍스트가 아니라 유닛이라고 해야 됨. 적은 김에 실행 컨텍스트 공부할 예정. 단순히 프로세서만 독점/공유하는게 아니라 프로세서, 메모리(코드, 데이터, 스택, 힙), 레지스터, 프로그램 카운터 등 컴퓨팅 자원을 독점/공유하는 것이 더 정확함.
- B-tree는 키워드에 없던 것 같은데 나와서 아직 학습 전이라고 냄.
- 최소 신장 트리 경로 구하는 거랑 가중치 구하는 건 그냥 맛보기 문제
실행 컨텍스트 찾아 봄.
프로세스나 스레드가 실행되는 동안 필요한 정보를 담고 있는 데이터 구조
레지스터 값, 프로그램 카운터(PC), 메모리 관리 정보, CPU 스케쥴링, I/O 상태 등
컨텍스트 스위칭이 일어나면 프로세스(스레드)의 상태가 실행 컨텍스트에 저장되고, CPU를 다시 점유하면 저장된 실행 컨텍스트를 불러와서 다시 프로세스(스레드) 재개
실행 컨텍스트는 메모리에 저장된다고 함.
여기서 드는 의문. 실행 컨텍스트를 메모리에 저장하면 CPU로 다시 올라갈 때 너무 느리지 않아?
다양한 최적화 기법이 사용된다고 함. 자주 사용되는 컨텍스트는 캐시에 올려놓음. 실행 컨텍스트 자체가 용량이 크지 않다고 함.
가상 메모리
램과 하드디스크를 하나로 합쳐서 추상화한 것
B-tree
이진 검색 트리(BST)를 응용
비트리는 모든 리프 노드가 같은 레벨이 있다.
즉, 평균, 최악의 경우에도 시간 복잡도는 O(log N)
차이는 BST는 자녀노드가 최대 2개이지만, B-tree는 자녀 노드를 2개 이상 가질 수 있음.
인터널 노드의 키가 x라면 자녀 노드는 x+1개여야 한다.
마찬가지로 노드의 키는 자녀 노드 - 1이 된다.
m차 비트리에서 자식 노드는 최소 m/2(올림)이다.
최대 M개의 자녀를 가질 수 있는 B-tree를 M차 B-tree라고 한다.
(최대 자녀가 3인 경우 3차 비트리)
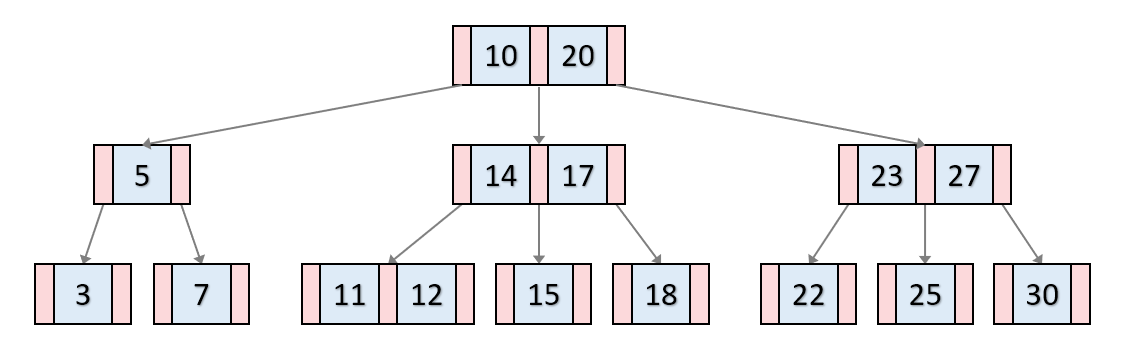
B-tree의 이름이 왜 'B'인가에 대해서는 명확한 답은 없지만,
Balanced의 약자이거나 B-tree를 고안한 Bayer, 또는 그가 일했던 보잉 과학 연구소(Boeing Scientific Research Labs) 약어라는 설이 있음.
스터디
알고리즘 시뮬레이션
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
백준 14888 연산자 끼워넣기
고군분투하다가 GPT 혹사시킴
import sys
def dfs(i, n, array, result, ops):
# 모든 수를 다 사용했을 때, 최대/최소값 반환
if i == n:
return [result]
results = []
# 각 연산자에 대해 재귀 호출
if ops[0]: # add
results.extend(dfs(i + 1, n, array, result + array[i], [ops[0]-1, ops[1], ops[2], ops[3]]))
if ops[1]: # sub
results.extend(dfs(i + 1, n, array, result - array[i], [ops[0], ops[1]-1, ops[2], ops[3]]))
if ops[2]: # mul
results.extend(dfs(i + 1, n, array, result * array[i], [ops[0], ops[1], ops[2]-1, ops[3]]))
if ops[3]: # div
results.extend(dfs(i + 1, n, array, int(result / array[i]), [ops[0], ops[1], ops[2], ops[3]-1]))
return results
n = int(sys.stdin.readline())
array = list(map(int, sys.stdin.readline().strip().split()))
ops = list(map(int, sys.stdin.readline().strip().split()))
results = dfs(1, n, array, array[0], ops)
print(max(results))
print(min(results))파이썬 1e9
수학적 지수 표기법
기수e지수 = 기수*10 ^ 지수
10억: 1e9 = 10^9
-10억: -1e9 = -10^9
백준 1916 최소비용 구하기
오!! 100% 혼자서 풀었음!
문제 보자마자 다익스트라 떠올렸고, 코드 짜서 한 번에 성공함!!!
다익스트라 이해하려고 하루 종일 씨름했는데,
한번 이해하고 나니까 퀴즈 문제도 쉽게 풀었고,
백준도 금방 풀었음!
문제 무조건 양치기로 하기보다는 기본 개념을 확실히 이해하고 넘어가기!
백준 골드5 '중'문제였는데 한번에 풀다니.. 기쁘다..
왠지 오전에 70%만 풀었다고 한 문제도 다익스트라로 혼자 풀 수 있을 것 같다!
import sys
import heapq
from collections import defaultdict
N = int(sys.stdin.readline().strip())
M = int(sys.stdin.readline().strip())
edges = []
for _ in range(M):
u, v, weight = map(int, sys.stdin.readline().strip().split())
edges.append((u, v, weight))
start, end = map(int, sys.stdin.readline().strip().split())
graph = defaultdict(list)
for edge in edges:
u, v, weight = edge
graph[u].append((weight, v))
def dijkstra(graph, n, start):
INF = float("inf")
distances = [INF] * (n + 1)
queue = []
heapq.heappush(queue, (0, start))
distances[start] = 0
while queue:
weight, current_node = heapq.heappop(queue)
if distances[current_node] < weight:
continue
for weight, adj_node in graph[current_node]:
new_distance = distances[current_node] + weight
if new_distance < distances[adj_node]:
distances[adj_node] = new_distance
heapq.heappush(queue, (new_distance, adj_node))
return distances
print(dijkstra(graph, N, start)[end])
스터디
인접 행렬은 불필요하게 0을 많이 넣어야 하니까 공간 복잡도에서 손해
하지만 특정 노드가 연결되어있는지는 O(1)
백준에서도 인접행렬로 메모리 초과가 뜬 문제를 인접 리스트도 바꿔서 통과함.






