7:40 입실
코딩하는 꿈 꿨음. 뭔가 자고 일어났는데 공부한 것 같다.
오늘은 위상정렬, 트라이, 다익스트라, 플로이드 와샬
위에 거 다 훑으면 기본 개념 끝! 문제 풀 수 있음!
백준 2178번 미로 탐색 다시 풀기
혼자서는 못 풀겠음. 이해하면서 따라쳐 봄
미로탐색에서 x가 변하는 건 상하가 움직임
y가 변하는 건 좌우로 움직임
import sys
from collections import deque
def bfs(current_x, current_y, end_x, end_y, maze):
# x가 변하는 건 하, 상
dx = (-1, 1, 0, 0)
# y가 변하는 건 우, 좌
dy = (0, 0, 1, -1)
queue = deque()
queue.append((current_x - 1, current_y - 1))
while queue:
current_x, current_y = queue.popleft()
for i in range(4):
next_x = current_x + dx[i]
next_y = current_y + dy[i]
if next_x < 0 or next_x >= end_x or next_y < 0 or next_y >= end_y:
continue
if maze[next_x][next_y] == 0:
continue
if maze[next_x][next_y] == 1:
maze[next_x][next_y] = maze[current_x][current_y] + 1
queue.append((next_x, next_y))
return maze[end_x - 1][end_y - 1]
N, M = map(int, sys.stdin.readline().strip().split())
maze = []
for _ in range(N):
maze.append(list(map(int, sys.stdin.readline().strip())))
print(bfs(1, 1, N, M, maze))오류 복기
2차원 배열 익숙하지 않아서 실수함
return maze[end_x - 1][end_y - 1]을
return maze[end_x - 1, end_y - 1]라고 적음.
변수명 변경할 때 전부 변경하지 않아서 틀림
for문 안에 있어야 할 코드가 밖에 있어서 틀림
BFS는 큐(deque)를 쓴다는 것 기억하기!
(DFS는 스택)
위상 정렬을 이해하기 위해서
위상 정렬을 이해하기 위해서는 먼저 DAG를 알아야 한다.
DAG에서만 위상 정렬이 가능하다!
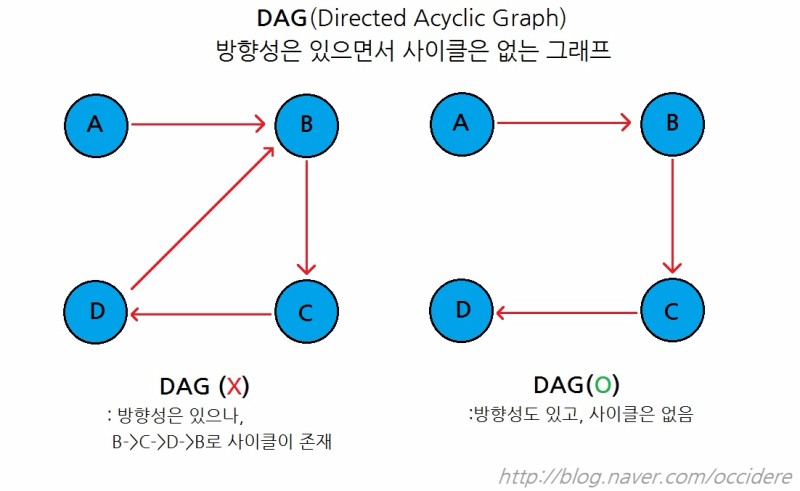
비순환 그래프(Directed Acyclic Graph)
- 사이클이 없는 (시작점에서 출발하면 다시 시작점으로 돌아올 수 없음)
- 유방향 그래프(간선은 한 방향으로만)
(우선순위를 나타내기 위해 주로 사용)
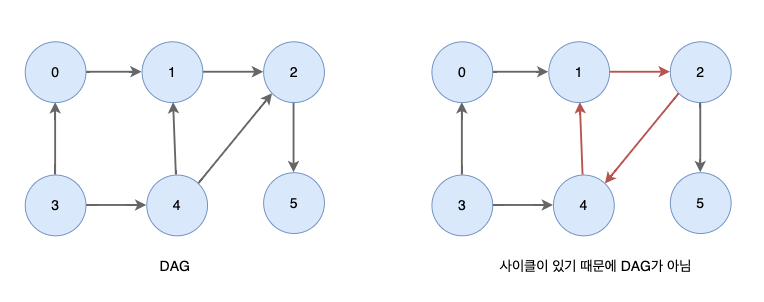
위상 정렬(topological sorting)이 뭐야?
유향 그래프의 꼭짓점을 변의 방향을 거스르지 않도록 나열하는 것
지금까지의 정렬은 '수'를 정렬하는 것이었다면 위상 정렬은 그래프를 정렬하는 것
진입 차수의 비 내림차순 순서로 정렬한다!
진입 차수: 각 노드로 들어오는 간선의 수
비 내림차순 순서: 비감소 순서, 동일한 값인 경우 상대적 순서가 중요하지 않음
진입차수가 동일한 경우 순서는 상관 없이 정렬한다!
즉 위상 정렬 결과는 여러 개가 나올 수 있다.
정렬 방법은 DFS를 이용하는 방법과 진입차수를 이용하는 방법(BFS)이 있다.
DFS탐색 결과를 역으로 하면 위상정렬과 같다.
위상 정렬 실행 방법
- 인접 리스트 형식으로 그래프 생성, 노드별 진입차수 기록
- 큐를 2개 생성
2.1 탐색 큐: 탐색할 노드를 저장
2.2 결과 큐: 정렬 결과를 저장 - 진입 차수가 0인 노드를 탐색 후 탐색 큐에 저장
(진입 차수가 0이면 정렬이 완료된 것!) - 탐색 큐에서 노드를 pull하고 결과 큐에 push
- 탐색 큐에서 뽑은 노드와 연결된 노드들의 진입차수를 -1
(직전 노드가 제거되어 다음 노드 입장에서는 진입차수가 1이 줄어들었기 때문) - 진입 차수 수정 결과가 0인 노드가 있으면 탐색 큐에 넣음.
4~6 과정을 탐색 큐가 빌 때까지 반복
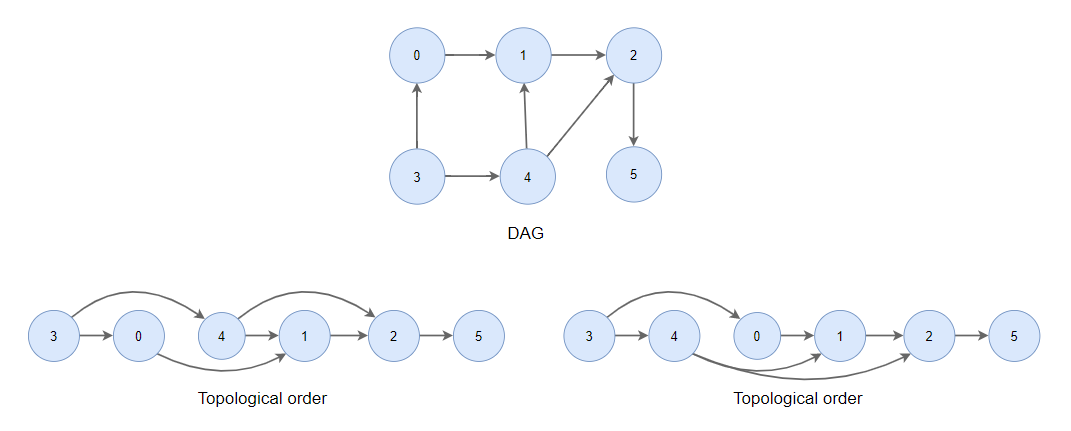
백준 2252 (줄 세우기) 위상정렬
아직 혼자는 못 풂. 여러 번 연습해보기!
import sys
from collections import deque, defaultdict
def topological_sort(N, edges):
# 그래프와 진입차수 초기화
graph = defaultdict(list)
indegree = [0] * (N + 1)
# 간선을 바탕으로 그래프 생성 및 최초 진입차수 정리
for edge in edges:
u, v = edge
graph[u].append(v)
indegree[v] += 1
# 결과와 큐 생성
result = []
queue = deque()
# 최초 진입차수가 0인 노드 큐에 삽입
for i in range(1, N + 1):
if indegree[i] == 0:
queue.append(i)
# 큐가 빌때까지 반복
while queue:
current_node = queue.popleft()
result.append(current_node)
# 정렬이 완료된 자식 노드들의 진입차수를 1 감소
for adj_node in graph[current_node]:
indegree[adj_node] -= 1
# 진입차수가 감소된 노드 중에서 진입차수가 0이면 큐에 삽입
if indegree[adj_node] == 0:
queue.append(adj_node)
return result
N, M = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
print(" ".join(map(str, topological_sort(N, edges))))백준 2252 (줄 세우기) 위상정렬 혼자 연습
80% 정도 혼자 풀었음
위상 정렬은 진입차수를 관리해야 함!
import sys
from collections import deque, defaultdict
def topological_sort(N: int, edges: list[tuple[int, int]]) -> list:
queue = deque()
indegree = [0] * (N + 1)
result = []
# 초기 진입차수를 업데이트한다
graph = defaultdict(list)
for edge in edges:
u, v = edge
graph[u].append(v)
indegree[v] += 1
# 진입차수가 0인 노드를 큐에 넣는다
for i in range(1, N + 1):
if indegree[i] == 0:
queue.append(i)
# 큐가 빌때까지 반복한다
while queue:
current_node = queue.popleft()
result.append(current_node)
for adj_node in graph[current_node]:
indegree[adj_node] -= 1
if indegree[adj_node] == 0:
queue.append(adj_node)
return result
N, M = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
print(" ".join(map(str, topological_sort(N, edges))))트라이 trie가 뭐야
탐색 트리의 일종
동적 집합이나 연관 배열을 저장하는 데 사용되는 트리 자료 구조
(글자 찾을 때 사용할 수 있음)
꼭 이진 트리는 아님.
다음 노드가 있으면 노드로 내려가고 없으면 노드를 생성
공간 복잡도가 올라가지만, 시간 복잡도는 내려 감
tried이 루트는 언제나 0
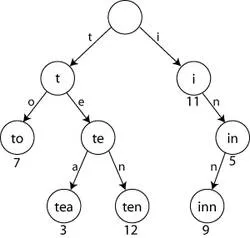
트라이는 노드가 직접적으로 값을 갖지 않는다!!
연관된 키(자식 노드)만 저장한다.
즉, 키의 값 자체가 자료구조 전반에 분산되는 형태
자식들을 조합해서 키의 값을 구하는 것!
값을 저장할 수는 있지만 일반적인 트라이 사용례가 아님!
트라이 어떻게 구현해?
배열, 해시맵으로 구현 가능
각 노드마다 현재 노드가 트리의 끝(리프인지)인지를 표시하는 값과
다음 노드가 해시맵 형태로 들어감.
트라이 자료구조 hands-on(클래스 기반)
class TrieNode:
def __init__(self):
# 자식 노드
self.children = {}
# 단어의 끝인지 확인하는 플래그
self.is_end_of_word = False
class Trie:
def __init__(self):
# 아무 것도 없는 루트 노드 생성
self.root = TrieNode()
def insert(self, word: str) -> None:
"""단어를 Trie에 삽입"""
node = self.root # 루트 노드에서 시작
for char in word: # 한 글자씩 순회
# 현재 문자가 자식 노드에 없으면 새 노드를 생성
if char not in node.children:
node.children[char] = TrieNode()
node = node.children[char] # 현재 주목 노드를 새로 생성한 노드로 변경
node.is_end_of_word = True
def search(self, word: str) -> bool:
"""단어가 Trie에 있는지 확인"""
node = self.root
for char in word:
# 검색하다가 자식에 다음 글자가 없으면 찾는 글자 없다는 뜻
if char not in node.children:
return False
# 만약 다음 글자가 있으면 주목 노드를 다음 노드로 변경
node = node.children[char]
return node.is_end_of_word # 해당 단어가 끝인지 아니면 어떤 단어의 일부인지 체크
def starts_with(self, prefix: str) -> bool:
"""단어가 주어진 접두사로 시작하는지 확인"""
node = self.root
for char in prefix: # 프리픽스를 한 글자씩 순회
if char not in node.children: # 다음 노드에 글자가 없으면 해당 접두사 없다는 뜻
return False
node = node.children[char] # 다음 글자가 있으면 주목 노드를 다음 노드로 변경
return True
trie = Trie()
trie.insert("apple")
print(trie.search("apple"))
print(trie.search("pop"))
print(trie.starts_with("app"))
print(trie.search("appl"))트라이 자료구조 hands-on(함수 기반)
클래스 기반은 각 함수에 root를 안 넘겨도 됐는데(self를 넘기니까)
함수 기반은 각 함수에 root를 넘겨줘야 함.
(원리는 똑같음. 클래스는 self를 받아서 그 안에서 루트를 찾음)
def create_trie_node():
return {"is_end_of_word": False, "children": {}}
def insert(root, word):
node = root
for char in word:
if char not in node["children"]:
node["children"][char] = create_trie_node()
node = node["children"][char]
node["is_end_of_word"] = True
def search(root, word):
node = root
for char in word:
if char not in node["children"]:
return False
node = node["children"][char]
return node["is_end_of_word"]
def starts_with(root, prefix):
node = root
for char in prefix:
if char not in node["children"]:
return False
node = node["children"][char]
return True
trie_root = create_trie_node()
insert(trie_root, "apple")
print(search(trie_root, "apple"))
print(search(trie_root, "app"))
print(starts_with(trie_root, "app"))다익스트라(Dijkstra)
그래프에서 정점 간의 최단 경로를 찾는 알고리즘!
도로 교통망 등에 활용(구글맵이나 네이게이션에 활용)
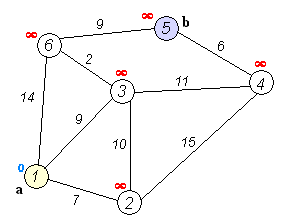
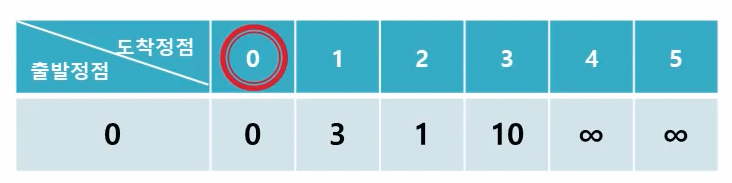
다익스트라는 하나의 출발 정점을 기준으로 모든 정점의 거리를 각각 계산한다.
플로이드 와샬 잠깐 정리
하나의 정점에서 다른 모든 정점까지의 최단 경로 : 다익스트라
모든 정점에서 모든 정점까지의 최단 경로 : 플로이드 와샬
다익스트라 어떻게 구현하지?
- 시작 노드 설정
- 모든 노드에 대한 거리를 무한대로 초기화, 시작 노드 거리는 0
(distance 1차원 배열 만듦) - 방문하지 않는 노드 중 가장 최단 거리가 짧은 노드 선택(그리디 방식)
- 선택된 노드로 가는 거리를 계산하여 기존보다 짧으면 업데이트
- 모든 노드 방문할 때까지 반복
다익스트라랑 프림 알고리즘이랑 같은 거 아닌가?
비슷하지만 같지 않음!
다익스트라는 최단 거리를 찾는 것이 목적!
프림은 간선의 가중치가 최소가 되는 최소신장트리를 찾는 것이 목적!
다익스트라는 양수 가중치인 경우에만 적용 가능!
다익스트라 hands-on
파이썬에서 무한대 수 지정하는 방법
float("infinity")or `float("inf")
BST처럼 뭔가 근접한 애들을 탐색하는 건 일반적으로 큐를 쓰는 것 같음.
(순서 상관없이 탐색하는 건 리스트 형태의 큐를 쓰면 되고, 작은 것부터 꺼내거나 할 때는 우선순위 큐를 씀.)
다익스트라를 이해하기 쉽게 비유적으로 표현해 봄!
우선 노드와 그 노드로 들어오기 위한 간선이 세트임.
노드와 간선을 따로 따로 생각하면 시뮬레이션을 해보다가 헷갈림.
노드와 간선을 따로 생각하지 말고, 간선의 가중치를 그 노드에 들어오는 입장료라고
생각하면 노드와 간선이 하나의 세트로 묶여서 이해가 더 쉬움!
간선의 가중치를 그 도시를 들어오는(다른 도시에서 들어올 때 드는 소모되는) 비용이라고 생각하고
한 번 도시를 들어오면 되돌릴 수 없음.
import heapq
def dijkstra(graph, start):
distances = {node: float("infinity") for node in graph}
distances[start] = 0
queue = []
heapq.heappush(queue, (distances[start], start))
print(f"힙에 {(distances[start], start)}를 넣습니다.")
while queue:
# 여기서 currnet_distance는 출발지로부터 현재까지 확인된 최단 거리
current_distance, current_node = heapq.heappop(queue)
print(f"힙에서 {(current_distance, current_node)}를 꺼냅니다.")
# 새롭게 추가해서 확인하려는 길이가 기존 최단거리보다 크면 로직을 돌릴 필요가 없음.
# 왜냐면 우선순위큐이기 때문에 과거에 비싼 경로가 추가되어 있는데, 그게 나중에 팝될 수도 있음.
# 새롭게 갱신된 (노드 & 최단거리)를 과거에 이미 힙에 추가된 건 그대로 남아 있기 떄문에 그걸 체크함.
if distances[current_node] < current_distance:
print(f"구버전의 노드 정보입니다. 현재까지의 최단거리인 {distances[current_node]}보다 {current_distance}가 크므로 다음 노드를 탐색하지 않습니다.")
continue
# 현재 노드를 통해 인접노드로 가는 길이를 계산함
for adj_node, weight in graph[current_node].items():
distance = current_distance + weight
# 현재 노드를 통해 인접 노드로 접근하는 게 기존보다 더 짧다면
if distance < distances[adj_node]:
print(f"{adj_node}의 최단거리를 기존 {distances[adj_node]}에서 {distance}로 갱신합니다.")
distances[adj_node] = distance
heapq.heappush(queue, (distance, adj_node))
print(f"힙에 {(distance, adj_node)}를 넣습니다.")
else:
print(f"{adj_node}의 현재 최단거리 {distances[adj_node]}보다 새로 계산된 {distance}가 더 크므로 다음 노드를 탐색하지 않습니다.")
print("우선순위큐가 비었습니다. 모든 탐색이 완료되었습니다.")
return distances
# 그래프
graph = {
"A": {"B": 2, "D": 10},
"B": {"C": 3, "D": 5},
"C": {},
"D": {"C": 1},
}
print(dijkstra(graph, "A"))
힙에 (0, 'A')를 넣습니다.
힙에서 (0, 'A')를 꺼냅니다.
B의 최단거리를 기존 inf에서 2로 갱신합니다.
힙에 (2, 'B')를 넣습니다.
D의 최단거리를 기존 inf에서 10로 갱신합니다.
힙에 (10, 'D')를 넣습니다.
힙에서 (2, 'B')를 꺼냅니다.
C의 최단거리를 기존 inf에서 5로 갱신합니다.
힙에 (5, 'C')를 넣습니다.
D의 최단거리를 기존 10에서 7로 갱신합니다.
힙에 (7, 'D')를 넣습니다.
힙에서 (5, 'C')를 꺼냅니다.
힙에서 (7, 'D')를 꺼냅니다.
C의 현재 최단거리 5보다 새로 계산된 8가 더 크므로 다음 노드를 탐색하지 않습니다.
힙에서 (10, 'D')를 꺼냅니다.
구버전의 노드 정보입니다. 현재까지의 최단거리인 7보다 10가 크므로 다음 노드를 탐색하지 않습니다.
우선순위큐가 비었습니다. 모든 탐색이 완료되었습니다.
{'A': 0, 'B': 2, 'C': 5, 'D': 7}다익스트라는 하나의 정수 값을 반환하는 게 아니라
시작 노드부터해서 각 정점까지의 최단거리를 계산하는 것!
다익스트라 핵심
현재까지의 거리를 갱신해 나가면서 새롭게 계산되는 거리와 비교하는 것!
(다이나믹 프로그래밍이라고 할 수 있다. 메모이제이션.)
오류 복기
에지를 기준으로만 계산하려고 해서 다익스트라를 이해하지 못했음.
에지를 기준으로 하는게 아니라 현재 노드의 최단 거리 값을 기준으로 갱신해 나가야 함.
다익스트라 시뮬레이션

인접 노드부터 탐색하려고해서 어려웠음. 그냥 우선순위 큐에 따라서 탐색하면 됨.
플로이드 와샬(floyed warshall)
모든 정점 간의 최단 경로를 찾는다
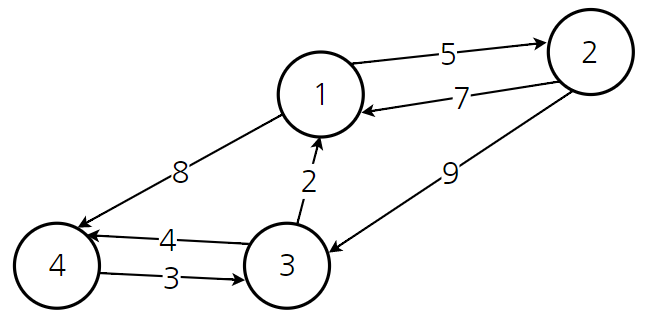
플로이드 와샬 어떻게 구현하지?
동적 프로그래밍이라고 볼 수 있음.
완전 탐색 방법
동적 프로그래밍(dynamic programmin) 어이 없는 거 찾음
왜 하필 다이나믹(동적) 프로그래밍이냐?
'다이나믹'이라는 이름이 붙은 이유는 이 방법을 개발한 Richard Bellman이 그냥 멋있어 보이는 이름을 정한 거임.(진심)
동적 프로그래밍은 컴퓨터에만 국한되지 않고 문제를 해결하는 일반적인 방법론으로 볼 수 있음.
큰 문제를 작은 문제로 쪼개고 작은 문제의 정답을 저장하고, 전체 문제의 정답을 찾는 것
중간 노드를 기반으로 작동한다.
(a, b 가 구하려는 각 정점, k는 중간 노드)
distance[a][b]=min(distance[a][b],distance[a][k]+distance[k][b])
- 모든 노드 쌍에 대한 거리를 무한대로 초기화(같은 노드 간의 거리는 0)
(distance 2차원 배열 만듦) - 그래프의 간선들에 대한 정보를 사용하여 거리 초기화
- 3중 반복문으로 모든 쌍에 대해 모든 중간 노드를 고려하여 거리를 갱신
예를 들어 15개의 정점이 있는 그래프가 있다고 하자.
그럼 중간노드 k를 먼저 설정하고, 모든 쌍(15 x 15 = 225)의 거리를 비교한다.
(i, j, k가 같은 경우도 검색함)
즉, k를 한번 순회할 때마다 225쌍을 탐색하고 이를 15번 시행하므로 225 x 15의 횟수가 필요한다.
시간 복잡도는 O(n^3)이다. (k, i, j를 각각 순회하므로 3중 반복문)
플로이드 와샬 hands-on
초창기 그래프는 각 노드별로 직접적으로 연결된 노드만 기록되어 있다.
즉, (연결되지 않은 것도 무한대로 표기하고) 모든 노드 쌍에 대한 거리를 비교하고
중간 노드를 선택 한 후,
중간 노드의 값과 중간 노드 기존 앞, 뒤를 합한 값을 비교해서 더 짧은 쪽으로 업데이트
def floyd_warshall(graph):
distance = graph.copy()
vertices = list(graph.keys())
for k in vertices:
for i in vertices:
for j in vertices:
distance[i][j] = min(distance[i][j], distance[i][k] + distance[k][j])
return distance
INF = float("inf") # 무한대 값
# 그래프 표현 (2차원 딕셔너리)
# 직접 연결되지 않은 정점들 간의 거리는 무한대로 설정
graph = {
"A": {"A": 0, "B": 5, "C": INF, "D": 10},
"B": {"A": 5, "B": 0, "C": 3, "D": INF},
"C": {"A": INF, "B": 3, "C": 0, "D": 1},
"D": {"A": 10, "B": INF, "C": 1, "D": 0},
}
distances = floyd_warshall(graph)
for node, distance in distances.items():
print(f"{node}: {distance}")
플로이드 와샬은 다익스트라에 비해 구현이 어렵지 않음!
가장 싼 항공권 찾기(직항 vs 경유)문제를 활용해서 풀 수 있을 것 같음!
플로이드 와샬의 궁금한 점
중간 노드를 1개 기준으로 완전 탐색을 하는데 그럼 중간노드 2개, 3개일 때는 고려하지 않는 거 아니야?
아님! 중간 노드로 탐색을 할 때 만약 더 싼 값이 있다면 그 값으로 업데이트가 되기 때문에,
단순히 중간 노드 1개일 때만을 비교하는게 아니라
한번 탐색을 거친 중간 노드로 인해 업데이트된 직항 노선이
사실상 이미 중간 노드를 경유한 값으로 반영된 것
플로이드는 그리디 알고리즘인가?
아니다! 그리디는 순간 순간 최적의 해를 구하는건데 플로이드는 한번 계산에서 최선의 해를 선택하는 건 아님. 이건 일부 구간의 비용을 그때그때 업데이트하고, 저장된 값으로 또 다른 경로의 비용을 계산한다는 측면에서 동적 프로그래밍(DP)라고 할 수 있음.
파이썬 문법: items()
딕셔너리에서 키와 밸류의 쌍을 튜플 형태로 반환하다.
반환된 값을 순환 가능한 객체라서 for문으로 돌릴 수 있고
튜플 언팩킹(다중 할당)도 가능하다!
dict = {"a": 10, "b": 20, "c": 30}
# dict_items 객체를 반환
# dict_items([('a', 10), ('b', 20), ('c', 30)])
print(dict.items())
# ('a', 10)
# ('b', 20)
# ('c', 30)
for item in dict.items():
print(item)
# a 10
# b 20
# c 30
for key, value in dict.items():
print(key, value)
깊은 복사 vs 얕은 복사
import copy
# 얕은 복사
copy.copy(a)
# 깊은 복사
copy.deepcopy(a)얕은 복사를 단순히 참조 값을 복사하는 것이라고 보면 안 됨.
얕은 복사는 객체 내부의 참조 타입은 참조값만 복사하고, 원시 타입은 실제 값을 복사함.
즉, 얕은 복사는 반(semi)복사라고 볼 수 있음.
딕셔너리를 기준으로 딕셔너리 안에 딕셔너리가 있으면 얕은 복사에서는 문제가 생길 수 있음.
복합 객체 내부에 복합 객체를 쓰면 얕은 문제에서는 문제가 발생할 수 있음.
(복사된 객체를 수정했는데 원복 객체가 수정되어 버림.)
스터디
최소 신장 트리는 방향성이 중요한 게 아니고 전체가 연결되어 있는 형태가 중심
전체 연결이 가장 효율적으로 연결되는 것(비용이 최소화되는 형태로 연결되는 것)
예) 도시 설계(도로), 통신 네트워크, 전력 그리드
최소 신장 트리(MST)
크루스칼: 간선 중심
-> 노드에 비해서 간선이 적을수록 (상대적으로) 유리하다.
-> 간선이 적은 그래프 희소 그래프라고 한다.
-> 간선이 점점 많아지면(완전 그래프에 가까워 질수록)
완전 그래프: 모든 정점이 서로 직접 연결된 그래프
프림: 노드 중심
-> 노드에 비해서 간선이 많으면 (상대적으로) 불리하다.
-> 간선에 비해서 노드가 적을수록 (상대적으로) 유리하다.
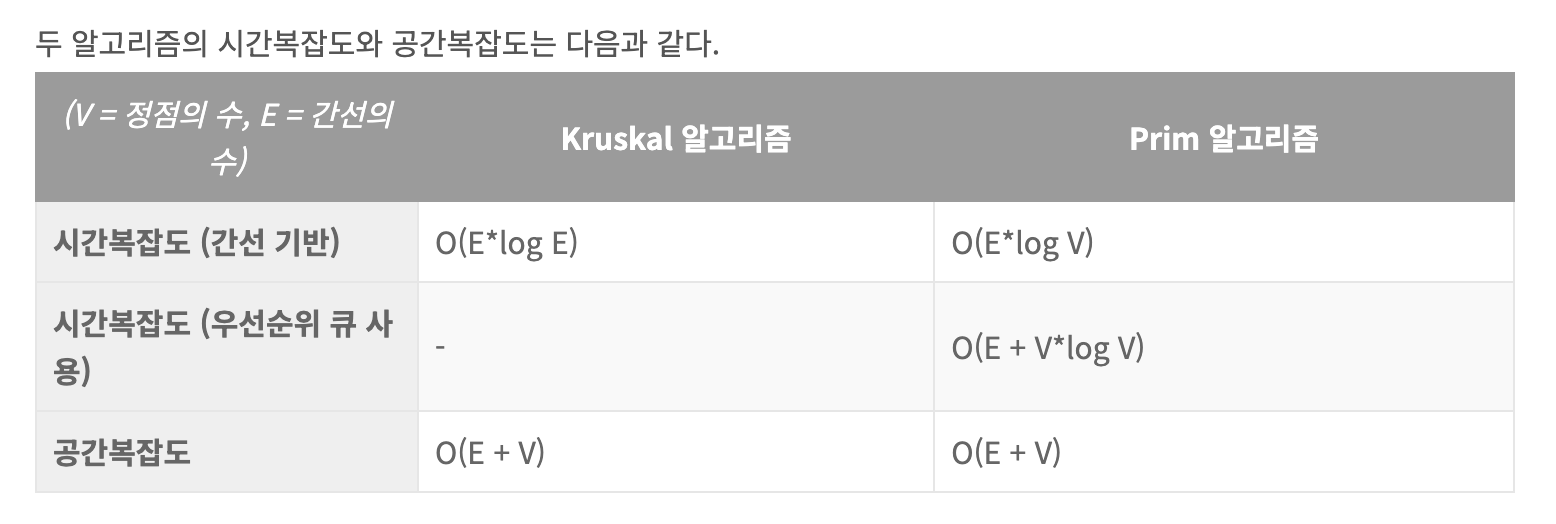
이번 주 핵심 개념 판서

