7:50 입실
어제 밤에 샤워하는데 화장실 벽에서 모기 발견
그 한 마리였음. 어제는 모기 없이 편하게 잠.
나오다가 습관적으로 방 키 뽑아들고 왔는데 룸메 키였음.
내려왔다가 다시 올라가서 꽂아놓고 옴.
오늘은 알고리즘 테스트..
자신은 없다.
시험 보기 전까지 '하' 문제 위주로 복습할 예정
백준 1991 트리 순회
깔끔하게 혼자 짜는 거 성공!
import sys
from collections import defaultdict
N = int(sys.stdin.readline().strip())
edges = []
for _ in range(N):
root, left, right = sys.stdin.readline().strip().split()
if left == '.':
left = None
if right == '.':
right = None
edges.append((root, left, right))
tree = defaultdict(list)
for edge in edges:
root, left, right = edge
tree[root] = ((left, right))
def dfs_preorder(tree, v, order=None, visited=None):
if order is None:
order = []
if visited is None:
visited = set()
if v:
left, right = tree[v]
order.append(v)
dfs_preorder(tree, left, order, visited)
dfs_preorder(tree, right, order, visited)
return order
def dfs_inorder(tree, v, order=None, visited=None):
if order is None:
order = []
if visited is None:
visited = set()
if v:
left, right = tree[v]
dfs_inorder(tree, left, order, visited)
order.append(v)
dfs_inorder(tree, right, order, visited)
return order
def dfs_postorder(tree, v, order=None, visited=None):
if order is None:
order = []
if visited is None:
visited = set()
if v:
left, right = tree[v]
dfs_postorder(tree, left, order, visited)
dfs_postorder(tree, right, order, visited)
order.append(v)
return order
print("".join(dfs_preorder(tree, 'A')))
print("".join(dfs_inorder(tree, 'A')))
print("".join(dfs_postorder(tree, 'A')))백준 5639 이진 검색 트리
기존 postorder=None 처리하는 방식 대신 extend를 써보려다가 90%정도 혼자 풀고 나머지 GPT 도움 받음.
extend는 None을 반환하는데 자꾸 반환값을 postorder에다가 할당하려고 그래서 생긴 문제. 그냥 extend를 했으면 해결 됐음.
import sys
sys.setrecursionlimit(10 ** 6)
preorder = []
while True:
try:
preorder.append(int(sys.stdin.readline().strip()))
except:
break
def pre_to_post(preorder):
postorder = []
if preorder:
root = preorder[0]
i = 1
while i < len(preorder):
if preorder[i] > root:
break
i += 1
postorder.extend(pre_to_post(preorder[1:i]))
postorder.extend(pre_to_post(preorder[i:]))
postorder.append(root)
return postorder백준 1260 DFS와 BFS
딕셔너리도 정렬할 수 있음. sorted를 하면 key값을 기준으로 오름차순 정렬됨.
오.. 이제 DFS, BFS그냥 후다다닥 코딩할 수 있음.(기본 문제만.. 응용 문제는 좀 어렵..)
import sys
from collections import defaultdict, deque
sys.setrecursionlimit(10 ** 6)
N, M, V = map(int, sys.stdin.readline().strip().split())
edges = []
for _ in range(M):
u, v = map(int, sys.stdin.readline().strip().split())
edges.append((u, v))
graph = defaultdict(list)
for edge in edges:
u, v = edge
graph[u].append(v)
graph[v].append(u)
def dfs_recursion(graph, v, order=None, visited=None):
if order is None:
order = []
if visited is None:
visited = set()
if v not in visited:
order.append(v)
visited.add(v)
for adj_node in sorted(graph[v]):
dfs_recursion(graph, adj_node, order, visited)
return order
def dfs_loop(graph, start_v):
order = []
visited = set()
stack = [start_v]
while stack:
current_node = stack.pop()
if current_node not in visited:
order.append(current_node)
visited.add(current_node)
for adj_node in sorted(graph[current_node], reverse=True):
stack.append(adj_node)
return order
def bfs_loop(graph, start_v):
order = []
visited = set()
queue = deque([start_v])
while queue:
current_node = queue.popleft()
if current_node not in visited:
order.append(current_node)
visited.add(current_node)
for adj_node in sorted(graph[current_node]):
queue.append(adj_node)
return order
print(" ".join(map(str, dfs_recursion(graph, V))))
# print(" ".join(map(str, dfs_loop(graph, V))))
print(" ".join(map(str, bfs_loop(graph, V))))
2주차 시험
2문제 풀었음. 완전 만족.
(정석대로 푼 건 아니라 답 맞추기에 급급했지만 김코치님께서 '우선 돌아가는 게 좋은 코드다. 최적화는 그 다음이다.'고 하셨으니까..)
2번 문제(2667 단지 번호 붙이기)가 익숙해 보여서 이거 먼저 했는데 70분 정도 걸림.=로 할당해야 하는데==쓰고 있어서 무한 루프 돌고 그랬음.
2번 문제 먼저 풀고 20분 밖에 없어서
1번 문제(1388 바닥장식)은 부호가 복잡해 보여서 거의 포기했는데,
세련된 기법은 아니지만 이중 반복문으로 11:29에 '맞았습니다!' 뜸!
쾌감 미쳤음.. 1분 남기고 풀다니..
김코치님 조언
눈 감고 모든 알고리즘 코드를 술술술 쓰지 못해도 괜찮음.
지금의 최소 기준은 '이 알고리즘이 어떤 것인지'를 인식하는 것.
'내가 무엇을 모르는지를 알는 게 가장 중요하다'
좋은 프로그램이란 '돌아가는 프로그램이다.' 현업에서도 우선 돌아가게 만들고 최적화는 다음에 한다.
3번 문제 발표하신 분 덕분에 이거 알게 됨.
PriorityQueue가 heapq를 통해 구현되었다고 함.
둘 중 뭐가 좋은건 없지만, 자유도가 더 높은 건 heapq
from queue import PriorityQueue백준 1388 바닥장식
import sys
N, M = map(int, sys.stdin.readline().strip().split())
floor = []
for _ in range(N):
floor.append(list(sys.stdin.readline().strip()))
left_to_right = 0
up_to_down = 0
for i in range(N):
temp = 0
for j in range(M):
if floor[i][j] == '-':
temp = 1
else:
left_to_right += temp
temp = 0
left_to_right += temp
for i in range(M):
temp = 0
for j in range(N):
if floor[j][i] == '|':
temp = 1
else:
up_to_down += temp
temp = 0
up_to_down += temp
print(left_to_right + up_to_down)
백준 2667 단지번호붙이기
import sys
from collections import deque
import copy
N = int(sys.stdin.readline().strip())
city_map = []
for _ in range(N):
city_map.append(list(map(int, sys.stdin.readline().strip())))
# start_node는 (x, y) 형태
def bfs(N, start_node):
global city_map
# 상, 하, 좌, 우
dx = (1, -1, 0, 0)
dy = (0, 0, 1, -1)
queue = deque()
queue.append((start_node))
count = 0
while queue:
x, y = queue.popleft()
if x < 0 or y < 0 or x >= N or y >= N:
continue
if city_map[x][y] == 0:
continue
city_map[x][y] = 0
count += 1
for i in range(4):
next_x = x + dx[i]
next_y = y + dy[i]
queue.append((next_x, next_y))
return count
results = []
for i in range(N):
for j in range(N):
if city_map[i][j] == 1:
count = bfs(N, (i, j))
results.append(count)
results = sorted(results)
total = len(results)
print(total)
for count in results:
print(count)
운영진 면담
앞으로는 공채가 아니라 추천에 의한 채용이 더 확대될 것.
(추천 후 코딩 테스트, 면접 보겠지만 가장 중요한 건 레퍼런스)
코딩, 하드스킬을 늘리는 것도 중요하지만 소프트스킬이 더 중요하다.
함께 일하고 싶은 매력적인 사람이 되어라.
현업에서는 라이브러리 직접 만들어 쓰는 경우 있다.
왜 이미 있는 걸 만드냐? 기성품은 성능 등에서 만족스럽지 못한 경우도 있다.
CS를 모르면 이런 걸 못한다.
남이 만든 걸 가져다만 쓸 수 있다.
이런 걸 할 수 있는 개발자는 많지 않다. 그런 개발자가 되어야 한다.
CSAPP 3장프로그램의 기계 수준 표현
1. 역사
x86-64
x86은 intel 8086 마이크로프로세서와 그 후속 제품군 지칭 명칭
x86 = 아키텍처
뒤에 숫자 = 확장 비트
1-1. CISC(x86) vs RISC(ARM)
둘 다 명령어 집합이라는 것 기억하기
CISC
Complex Instruction Set Computer
설계 철학: 하나의 명령어로 다양한 작업을 수행
- 복잡하고 가변 길이 명령어 세트 사용(복잡한 연산을 하나의 명령어로 수행)
- 명령어마다 다양한 클록 사이클 필요
- 메모리와 레지스터 간의 직접적인 데이터 이동에 중점
(메모리로부터 직접 데이터를 읽거나 쓰는 명령어, 메모리 접근 빈번)
(move, load, store, push, pop, add/substract, increment, decrement, compare 등...) - 복잡한 명령어들은 내부적으로 마이크로 코드를 사용하여 여러 단계로 나누어짐
(복잡한 명령어가 들어오면 cpu의 마이크로코드 엔진에 의해 여러 단계로 나뉘어 실행)
(마이크로코드는 전용 공간인 마이크로코드 ROM이나 유사한 하드웨어에 저장되어 있음)
(CISC도 마이크로코드마다 1클록 주기로 실행됨) - 다양한 기능을 제공하는 복잡한 명령어가 있지만 자주 쓰이는 것만 쓰이고,
나머지 복잡한 명령어는 잘 안 쓰임
(논문에 따르면 20% 명령어가 80% 기능을 수행) - 명령어 파이프라인 불리(실행 클럭도 다르고 하나의 명령어가 너무 복잡)
- 전통적인 PC, 노트북, 서버 등
- 메모리가 충분치 않았던 초창기에 사용됨(명령어가 차지하는 메모리 최대한 줄여서 프로그램 용량 줄최소화)
RISC
Reduced Instruction Set Computer
설계 철학: 간단하고 빠른 명령어들로 복잡한 작업을 수행
- 간단하고 고정 길이 명령어 세트 사용(복잡한 연산은 다양한 명령어를 조합해서 수행)
- 대부분 명령어들이 단일 클록 사이클 내에서 실행(3 GH는 1초에 30억 연산, 1클록 = 0.33ns)
- 메모리와 레지스터 간의 직접적인 데이터 이동보다 레지스터 내부에서의 연산 및 데이터 이동이 주
(메모리 직접 접근을 최소화한다. 기본 메모리 명령어는 load, store로 한정) - 간소화된 명령어로 인해 파이프라이닝(동시에 여러 명령어 실행 기술) 수현이 쉬움
- 저전력, 임베디드, 모바일에 주로 사용
CISC와 RISC에서 덧셈을 실행하는 방법 비교
1. CISC
(이거 한 줄로 끝)
ADD MEM1, MEM2, MEM3실행 과정:
1. MEM1의 값을 CPU 내부의 임시 레지스터로 불러옵니다.
2. MEM2의 값을 또 다른 임시 레지스터로 불러옵니다.
3. 두 임시 레지스터의 값을 더합니다.
4. 결과를 MEM3에 저장합니다.
2. RISC
LOAD R1, MEM1
LOAD R2, MEM2
ADD R3, R1, R2
STORE MEM3, R3실행 과정:
1. MEM1의 값을 레지스터 R1로 불러옵니다.
2. MEM2의 값을 레지스터 R2로 불러옵니다.
3. 레지스터 R1와 R2의 값을 더하여 결과를 레지스터 R3에 저장합니다.
4. R3의 값을 MEM3에 저장합니다.
내부적으로 진행되는 단계는 비슷하다.
하지만 명령어 수준에서 어떻게 표현하고 처리하는지가 두 아키텍처의 차이
2. 프로그램의 인코딩
기계어 코드
익스트럭션 포맷: 하나의 명령어가 바이너리 필드들도 구성된 형식
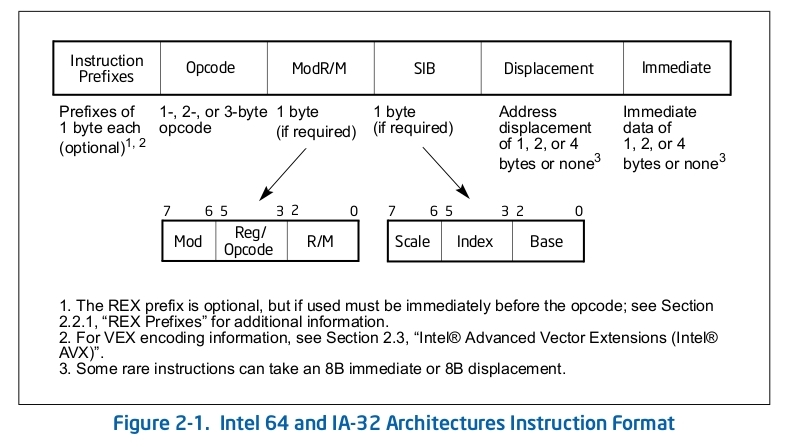
인스트럭션으로 CPU의 내부 구성요소들을 조작하거나 동작시킴
CPU 내부 구성 요소
프로그램 카운터: 실행 할 다음 인스트럭션의 메모리 주소
정수 레지스터 파일: 연산을 위한 일시적인 데이터 저장 공간 64비트 값 저장, 정수 데이터 저장
조건코드 레지스터 파일: 플래그 래지스터, 상태 레지스터. 가장 최근에 실행한 산술 또는 논리 인스트럭션 상태 저장(오버플로우, 제로, 부호 등)
벡터 레지스터: 하나 이상의 정수 또는 부동소수점 값들을 각각 저장(한 번의 연산으로 여러 데이터 요소에 동일한 연산 적용)
컴파일
처음으로 어셈블리어로 컴파일 해 보았다!
mstore.c
long mult2(long, long);
void multstore(long x, long y, long *dest) {
long t = mult2(x, y);
*dest = t;
}mstore.s
확장자 s는 소스파일이라는 뜻
s 확장자 소스파일은 기계어로 변환될 수 있다.
gcc -Og -S mstore.c
.section __TEXT,__text,regular,pure_instructions
.build_version macos, 12, 0 sdk_version 13, 1
.globl _multstore ; -- Begin function multstore
.p2align 2
_multstore: ; @multstore
.cfi_startproc
; %bb.0:
stp x20, x19, [sp, #-32]! ; 16-byte Folded Spill
stp x29, x30, [sp, #16] ; 16-byte Folded Spill
add x29, sp, #16
.cfi_def_cfa w29, 16
.cfi_offset w30, -8
.cfi_offset w29, -16
.cfi_offset w19, -24
.cfi_offset w20, -32
mov x19, x2
bl _mult2
str x0, [x19]
ldp x29, x30, [sp, #16] ; 16-byte Folded Reload
ldp x20, x19, [sp], #32 ; 16-byte Folded Reload
ret
.cfi_endproc
; -- End function
.subsections_via_symbolsmstore.o
gcc -Og -c mstore.c
CFFAEDFE 0C000001 00000000 01000000 04000000 68010000 00200000 00000000
19000000 E8000000 00000000 00000000 00000000 00000000 00000000 00000000
48000000 00000000 88010000 00000000 48000000 00000000 07000000 07000000
02000000 00000000 5F5F7465 78740000 00000000 00000000 5F5F5445 58540000
00000000 00000000 00000000 00000000 24000000 00000000 88010000 02000000
D0010000 01000000 00040080 00000000 00000000 00000000 5F5F636F 6D706163
745F756E 77696E64 5F5F4C44 00000000 00000000 00000000 28000000 00000000
20000000 00000000 B0010000 03000000 D8010000 01000000 00000002 00000000
00000000 00000000 32000000 18000000 01000000 00000C00 00010D00 00000000
02000000 18000000 E0010000 04000000 20020000 20000000 0B000000 50000000
00000000 02000000 02000000 01000000 03000000 01000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 F44FBEA9 FD7B01A9 FD430091 F30302AA 00000094 600200F9
FD7B41A9 F44FC2A8 C0035FD6 00000000 00000000 00000000 24000000 01000004
00000000 00000000 00000000 00000000 10000000 0300002D 00000000 01000006
19000000 0E010000 00000000 00000000 13000000 0E020000 28000000 00000000
01000000 0F010000 00000000 00000000 0C000000 01000000 00000000 00000000
005F6D75 6C747374 6F726500 5F6D756C 7432006C 746D7031 006C746D 70300000목적파일(.o)을 소스파일(.s)로 리버스 엔지니어링(역공학)
odjdump - mstore.o (오브젝트 파일 명령어)
mstore.o: file format mach-o arm64
Disassembly of section __TEXT,__text:
0000000000000000 <ltmp0>:
0: f4 4f be a9 stp x20, x19, [sp, #-32]!
4: fd 7b 01 a9 stp x29, x30, [sp, #16]
8: fd 43 00 91 add x29, sp, #16
c: f3 03 02 aa mov x19, x2
10: 00 00 00 94 bl 0x10 <ltmp0+0x10>
14: 60 02 00 f9 str x0, [x19]
18: fd 7b 41 a9 ldp x29, x30, [sp, #16]
1c: f4 4f c2 a8 ldp x20, x19, [sp], #32
20: c0 03 5f d6 ret확장자 .O가 실행 파일이 아님! 이건 목적 파일이고 링킹 후에 실행 가능한 실행파일이 생성되는 것!
링커가 여러 목적 파일을 모아 하나의 실행 파일로 만들어 주는 것!
링킹
실행 가능한 코드를 생성하기 위해서 링커를 목적코드들에 대해 실행해야 한다.
gcc Og -o prog main.c mstore.c
hello.c를 컴파일 했는데 hello.out이 아니라 hello가 생성되어 GPT 물어 봄
gcc hello.c -o hello
이유는 -o 옵션이 출력되는 파일명을 지정하는 거!
-o를 생략하면 a.out이 생성됨.
hello.c
#include <stdio.h>
int main () {
printf("Hello, World!\n");
return 0;
}**hello.o -> objdump -d hello
hello: file format mach-o arm64
Disassembly of section __TEXT,__text:
0000000100003f68 <_main>:
100003f68: ff 83 00 d1 sub sp, sp, #32
100003f6c: fd 7b 01 a9 stp x29, x30, [sp, #16]
100003f70: fd 43 00 91 add x29, sp, #16
100003f74: 08 00 80 52 mov w8, #0
100003f78: e8 0b 00 b9 str w8, [sp, #8]
100003f7c: bf c3 1f b8 stur wzr, [x29, #-4]
100003f80: 00 00 00 90 adrp x0, 0x100003000 <_main+0x18>
100003f84: 00 a0 3e 91 add x0, x0, #4008
100003f88: 05 00 00 94 bl 0x100003f9c <_printf+0x100003f9c>
100003f8c: e0 0b 40 b9 ldr w0, [sp, #8]
100003f90: fd 7b 41 a9 ldp x29, x30, [sp, #16]
100003f94: ff 83 00 91 add sp, sp, #32
100003f98: c0 03 5f d6 ret
Disassembly of section __TEXT,__stubs:
0000000100003f9c <__stubs>:
100003f9c: 10 00 00 b0 adrp x16, 0x100004000 <__stubs+0x4>
100003fa0: 10 02 40 f9 ldr x16, [x16]
100003fa4: 00 02 1f d6 br x16위 코드에 대한 GPT 해설
sub sp, sp, #32: 스택 포인터(sp)를 감소시켜 스택 프레임을 생성합니다.
이는 로컬 변수를 저장할 공간을 확보하는 것입니다.
stp x29, x30, [sp, #16]: x29(프레임 포인터)와 x30(링크 레지스터)를 스택에 저장합니다.
add x29, sp, #16: 현재 스택 포인터의 값을 x29에 저장합니다.
mov w8, #0: 0 값을 w8 레지스터에 할당합니다.
str w8, [sp, #8]: w8의 값을 스택의 특정 오프셋에 저장합니다.
stur wzr, [x29, #-4]: 0 값을 x29의 특정 오프셋에 저장합니다.
adrp x0, 0x100003000: 페이지 주소를 x0에 로드합니다.
add x0, x0, #4008: x0에 주소 오프셋을 추가합니다.
bl 0x100003f9c: 주어진 주소로 분기하고 현재 주소를 링크 레지스터(x30)에 저장합니다.
즉, _printf 함수를 호출하는 것으로 보입니다.
ldr w0, [sp, #8]: 스택에서 값을 w0 레지스터에 로드합니다.
ldp x29, x30, [sp, #16]: 스택에서 x29와 x30 값을 로드합니다.
add sp, sp, #32: 스택 프레임을 해제합니다.
ret: 현재 함수를 종료하고 x30에 저장된 주소로 돌아갑니다.3. 데이터의 형식
16비트 데이터 타입 = 워드
(이유는 원래 인텔 프로세서는 16비트 구조를 사용하다가 추후에 32비트로 확장되었기 때문)
32비트 = 더블워드
64비트 = 쿼드워드
C에서의 데이터 타입(x86-64)
표준 int: 4바이트 더블워드
포인터: 8바이트 쿼드워드
long: 8바이트 쿼드워드
float(단일 정밀도): 4바이트 더블워드
double(이중 정밀도): 8바이트 쿼드워드
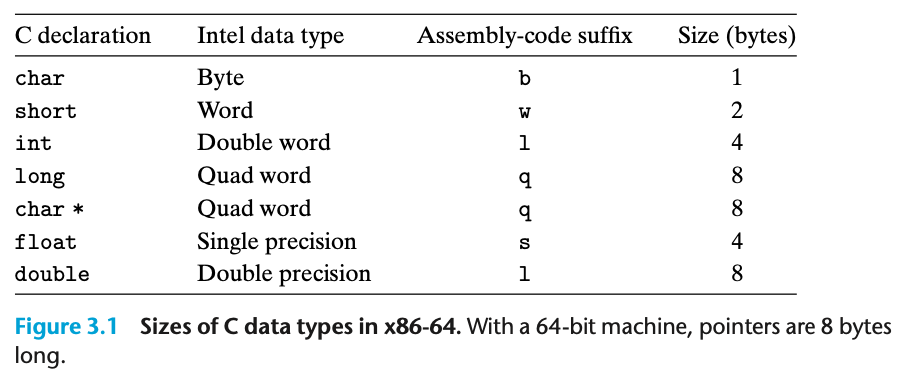
C가 있는데 어셈블리어로 코딩하는 경우가 있을까?
있다! 컴파일러가 훌륭하지만, C로 구현하지 못하는 기계어 수준의 코드들이 있다.
이때는 어셈블리어로 코딩 후 C와 연결할 수 있다.
동적 프로그래밍(DP)
지난 번에 공부함. 문제 풀어보자!
(요약하면 동적이라는 이름은 그냥 멋있어 보여서 붙인거고,
핵심은 문제를 작게 나누어 해를 저장(메모이제이션)하고 이를 모아서 전체 문제의 해를 구하는 철학)
백준 2748 피보나치 수2
재귀, 반복문 말고 DP로 풀어보자!
import sys
sys.setrecursionlimit(10**6)
n = int(sys.stdin.readline().strip())
def fib(n, mz=None):
if mz is None:
mz = [0] * (n + 1)
if mz[n] != 0:
return mz[n]
if n <= 2:
mz[n] = 1
return 1
mz[n] = fib(n - 1, mz) + fib(n - 2, mz)
return mz[n]
print(fib(n))
유튜브로 흐름만 먼저 보고 구현해서 성공!
마지막에 재귀 자체를 return해서 오류가 있었는데(mz에 저장을 안함)
mz에 저장 코드 넣고, 그 값을 리턴하게 바꾸니까 정상 동작!
백준 1904 01 타일
피보나치 수열인 것 찾았음.
기본 로직은 짰는데% 15746계속 못 풀어서 GPT 도움.
코드는 좀 깔끔하지 못하지만 해결은 함.
import sys
N = int(sys.stdin.readline().strip())
sys.setrecursionlimit(10**6)
def bi_loop(N):
if N == 1:
return N
mz = [1, 1]
temp = 0
for _ in range(N - 1):
a = mz[0]
b = mz[1]
temp = (a + b) % 15746
mz[0] = b
mz[1] = temp
return temp
print(bi_loop(N))GPT 코드
def bi_loop(N):
if N == 1:
return 1
mz = [1, 1]
for _ in range(N - 1):
mz[0], mz[1] = mz[1], (mz[0] + mz[1]) % 15746
return mz[1]
N = int(input())
print(bi_loop(N))오류 복기
요즘 자꾸 할당을==로 잘못하고 있음. 주의할 것!
정글러 강의
PID는 알고 있었는데 TID(쓰레드 아이디)를 알게 되었음.
TID를 LWP(Light Weight Process)라고도 함.
top명령어를 통해 실행 중인 프로세스의 동적인 실시간 뷰를 볼 수 있음.
(table of processes)
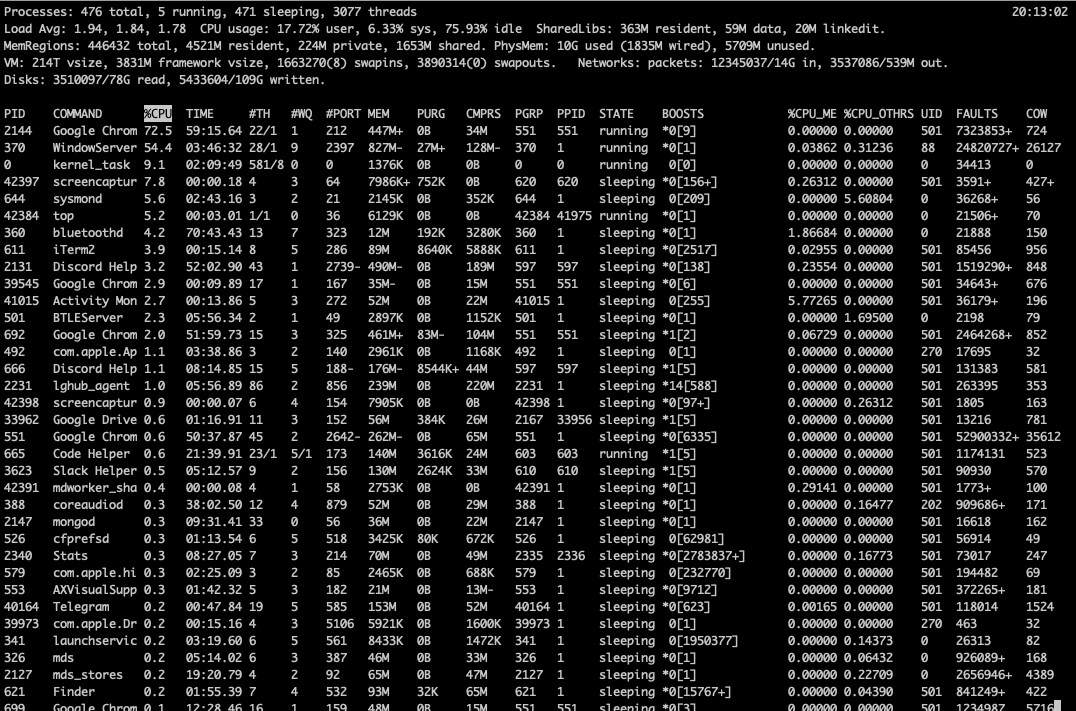
그리디 알고리즘
그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식
단, 근사 알고리즘이다. 100% 최적해를 보장하지는 않는다.
(어느 정도 적합한 수준의 해답)
2가지 조건이 있는 경우 그리디를 적용할 수 있다.
탐욕 선택 속성(greedy choice property)
: 매 선택이 지역적으로 최적이어야 한다.
: 현재의 선택이 이후 선택에 대한 정보나 가능성을 제거하면 안 된다.
(예를 들어, 주어진 예산 내에서 A책을 고르면 아직도 C책을 선택할 수 있는 여유가 있지만, B책을 먼저 고르면 예산 부족으로 C책을 선택할 수 없게 되는 상황에서는 그리디 알고리즘의 탐욕 선택 속성 조건을 충족하지 않는다.)
최적 부분 구조(optimal substructure)
: 부분해로 최적해를 구할 수 있다.
: 부분 문제의 해결 방법을 합치면 전체 문제의 최적해를 구할 수 있다.
백준 11047 동전 0
예전에 비슷한 문제 프로그래머스에서 풀어본 적 있어서 쉽게 풀었음.
제일 큰 가치부터 하나씩 사용하는 방식으로 그리디 방식이라고 할 수 있음.
import sys
N, K = map(int, sys.stdin.readline().strip().split())
coins = []
for _ in range(N):
coins.append(int(sys.stdin.readline().strip()))
count = 0
for coin in sorted(coins, reverse=True):
count += K // coin
K = K % coin
if K == 0:
break
print(count)백준 1541 잃어버린 괄호
'하'인데 코드 구현이 어려움.
풀이 흐름은 혼자 생각해 냄.
핵심 아이디어는 - 이후에 등장하는 +는 모두 -처럼 취급해도 됨.
입력값을 정리하는 게 어렵다.
import sys
s = sys.stdin.readline().strip().split("-")
result = 0
for num in s[0].split("+"):
result += int(num)
for i in s[1:]:
for num in i.split("+"):
result -= int(num)
print(result)분할 정복(Divide and Conquer)
한번에 해결 불가능한 전체 문제를 작은 문제로 분할하여 분할된 부분부터 해결
대표적으로 병합 정렬(머지 소트)
분할 -> 정복 -> 결합
1. 분할: 현재의 문제와 동일하지만 크기가 더 작은 다수 부분 문제로 분할
2. 정복: 부분 문제를 재귀적으로 정복(부분 문제 크기가 충분히 작으면 직접적으로 해결)
3. 결합: 부분 문제의 해를 결합해 원래 문제의 해로 만듦
