샐러드 냉장고에 넣고 오느라 좀 늦음
7:55 입실
오늘은 CSAPP 연습 문제 다 푸는 거 목표!
연습문제 3.3
movb $0xF, (%ebx)
%ebx 레지스터에 할당된 메모리 주소 값에 0xF 상수를 할당한다.
하지만 64비트 아키텍처에서 메모리 주소를 참조할 때는 64비트 레지스터를 사용해야 하는데
%ebx는 32비트 레지스터이기 때문에 잘못된 주소 지정 방식이다.
따라서 해당 레지스터에는 메모리 주소를 할당할 수 없다.
movl %rax, (%rsp)
%rsp는 64비트 레지스터이기 때문에 메모리 주소를 참조하는 레지스터로 사용할 수 있다.
%rax는 64비트 레지스터인데, 인스트럭션 접미사가 l로 32비트에 해당한다.
이 인스트럭션은 %rax의 모든 값을 가져오지 않고 하위 32비트만 가져온다.
(어셈블러가 이 인스트럭션은 허용하지 않아 에러 메시지 송출)
따라서 전체 64비트 값을 사용하려면 인스트럭션의 접미사를 q로 변경해야 한다.
movw (%rax), 4(%rsp)
%rax 메모리 주솟값을 참조하여 참조된 메모리 주소에서
2바이트(16비트)만큼의 값을 읽어 온 후 메모리 (4 + %rsp)에 저장한다.
단, x86 아키텍처 ISA(Instruction Set Architecture)에서
소스와 데스티네이션이 모두 메모리 주소로 사용될 수 없다.
movb %al, %sl
1바이트(8비트) 레지스터 %al값을 %sl레지스터로 이동한다.
하지만 %sl이라는 이름의 레지스터는 존재하지 않는다.
movq %rax, $0x123
64비트 레지스터 %rax에 할당된 값을 상수 $0x123로 이동한다.
어떤 값을 메모리 또는 레지스터가 아닌 상수(즉시값) 자체로 옮길 수 없기 때문에
목적지가 잘못되었다.
movl %eax, %rdx (문제 오타인 듯)
movl %eax, %dx
32비트 레지스터 %eax의 값을 16비트비트 레지스터 %dx로 이동한다.
접두어 l은 32비트를 의미하는데, 목적지의 레지스터 16비트는 크기 불일치로 인해 에러가 발생한다.
movb %si, 8(%rbp)
16비트 레지스터 %si의 값을 메모리 주소 (%rbp + 8)로 이동한다.
movb는 8비트 명령어인데, 이 경우 %si의 16비트와 크기가 불일치하기 때문에 에러가 발생한다.
8(%rbp)는 레지스터 자체에 값을 할당하는 게 아니라 메모리 참조값을 활용하기 때문에
movb와는 무관하다.
연습문제 3.4
// typedef로 선언된 자료형
src_t *sp;
dest_t *dp;
// 구현할 연산
*dp = (dest_t) *sp;| src_t | dest_t | Instruction |
|---|---|---|
| long | long | movq (%rdi), %rax movq %rax, (%rsi) |
| char | int | movsbl (%rdi), %eax movl %eax, (%rsi) |
| char | unsigned | movsbl (%rdi), %eax movl %eax, (%rsi) |
| unsigned char | long | movsbl (%rdi), %eax movl %eax, (%rsi) |
| int | char | movl (%rdi), %eax movb, %al, (%rsi) |
| unsigned | unsigned char | movl (%rdi), %eax movb, %al, (%rsi) |
| char | short | movsbw (%rdi), %ax movw, %ax, (%rsi) |
%rax에 할당된 값은 %eax, %ax, %al로도 하위 비트에 접근할 수 있다!
0으로 확장하는 데이터 이동 인스트럭션 movz
복사되는 원래 값에 상위 비트에 0을 추가하여 확장한다.(제로 확장)
부호에 관계없이 무조건 0으로 채움
movzbw: byte to word
movzbl: byte to double word
movzwl: word to double word
movzbq: byte to quad word
movzwq: word to quad word
movzlq는 없다! movl은 특별하게 상위 32비트를 0으로 채운다.
부호를 확장하는 데이터 이동 인스트럭션 movs
복사되는 원래 값은 상위 비트에 부호 비트(sign bit)를 추가하여 확장
원래 값이 양수면 0으로 확장, 원래 값이 음수면 1로 확장
movsbw
movsbl
movswl
movsbq
movswq
movslq
제로 확장, 부호 확장 모두 작은 데이터 타입의 값을 더 큰 데이터 타입의 레지스터로 복사할 때 활용
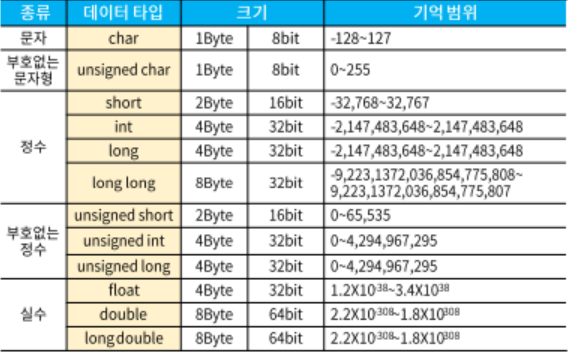
char는 주로 문자를 표현할 때 사용되지만 char자체가 문자를 나타내는 것이 아니라 1바이트 정수를 나타내는 데이터 타입이다. 따라서 unsigned char도 존재할 수 있는 것!
int도 4바이트, long도 4바이트?
long은 긴 정수형이다.
대부분의 아키텍처에서 int는 4바이트를 차지하지만,
long은 32비트 시스템에서는 4바이트, 64비트 시스템에서는 8바이트를 차지한다.
(이상한게 windows 64비트에서 long은 4바이트, macOS에서는 8바이트)
크로스 플랫폼 코드 작성할 때는 long타입은 쓰지 않는 것이 좋음.
연습문제 3.5
void decode1(long *xp, long *yp, long *zp);
// *xp 는 %rdi
// *yp 는 %rsi
// *zp 는 %rdxdecode1:
movq (%rdi), %r8 // 64비트 %rdi 메모리 값(xp의 값)을 %r8 레지스터로 이동
movq (%rsi), %rcx // 64비트 %rsi 메모리 값(yp의 값)을 %rcx 레지스터로 이동
movq (%rdx), %rax // 64비트 %rdx 메모리 값(zp의 값)을 %rax 레지스터로 이동
movq %r8, (%rsi) // xp의 값을 *yp 주솟값의 참조값으로 변경
movq %rcx, (%rdx) // yp의 값을 *zp 주솟값의 참조값으로 변경
movz %rax, (%rdi) // zp의 값을 *xp 주솟값의 참조값으로 변경
ret#include <stdio.h>
void decode1(long *xp, long *yp, long *zp)
{
long x = *xp;
long y = *yp;
long z = *zp;
*yp = x;
*zp = y;
*xp = z;
}
연습문제 3.6
%rbx에 p 저장
%rdx에 q 저장
%rax에 저장되는 값
(leaq는 movq와 비슷하지만 메모리에 직접 접근하지 않는다.)
leaq 9(%rdx), %rax
유효 주소 9 + q의 값을 %rax 레지스터에 할당한다.
leaq (%rdx, %rdx), %rax
유효 주소 q + p의 값을 %rax 레지스터에 할당한다.
leaq (%rdx,%rbx,3), %rax
유효 주소 q + 3p의 값을 %rax 레지스터에 할당한다.
leaq 2(%rbx,%rbx,7), %rax
유효 주소 2 + p + 7p = 2 + 8p의 값을 %rax 레지스터에 할당한다.
leaq 0xE(,%rdx,3),%rax
유효 주소 14 + 3q의 값을 %rax 레지스터에 할당한다.
leaq 6(%rbx,%rdx,7),%rax
유효 주소 6 + p + 7q의 값을 %rax 레지스터에 할당한다.
연습문제 3.7
short scale3(short x, short y, short z) {
short t = _______; // 10 * y + z + y * x
return t;
}short scale3(short x, short y, short z)
x in %rdi, y in %rsi, z in %rdx
scale3:
leaq (%rsi, %rsi, 9), %rbx // y + 9y = 10 * y 값을 %rbx에 저장
leaq (%rbx, %rdx), %rbx // 10 * y + z 값을 %rbx에 저장
leaq (%rbx, %rdi, %rsi), %rbx // 10 * y + z + y * x를 %rdx에 저장
ret오퍼랜드가 3개인 경우 연산
lead(base, index, scale)
leaq 명령어는 메모리 주소 계산을 위한 도구이지만 지금은 간단한 산술 연산 수행하는 것!
(최적화된 코드에서 볼 수 있는 기법)
leaq를 무조건 주소 연산에 쓴다고만 잘못 생각함. 메모리 접근 없이 이루어지는 연산을 leaq로 할 수 있음.
정리하면 leaq는 원래 목적이 메모리 주소를 계산하는 것이지만,
그 특성을 활용해서 레지스터 간의 산술 연산에도 사용할 수 있는 것! (성능상의 이점)
만약 이렇게 하지 않으면 stack 메모리에 중간 값을 저장하는 등의 불필요한 메모리 접근이 필요함.
mov와 lea는 뭐가 다르지?
mov는 기본적으로 메모리 접근을 염두한 명령어(메모리 값 복사, 전송 목적)
(레지스터 간, 메모리 -> 레지스터, 레지스터 -> 메모리 등 다양한 경우에 사용)
mov는 소스에서 목적지로 값을 전송하는 것이 주요 기능
lea는 메모리 접근을 염두하지 않은 명령어(유효 주소 계산 목적)
그렇지만 mov도 오퍼랜드에 메모리 주소가 아니라 레지스터만 사용하면 메모리 접근 없이 동작이 발생함
lea는 주소를 계산하고 그 계산 값을 목적 레지스터에 저장하는 게 목표
다음 두 명령어는 같은 결과를 주지만 사용하는 방식과 목적이 다르다!
mov %rax, %rbx // %rax에 저장된 값을 %rbx로 복사
lea (%rax), %rbx // %rax에 저장된 값을 (유효 주소를 계산한 후) %rbx로 복사
mov는 데이터의 '복사'가 주 목적이라는 것 기억!
lea는 유효 주소를 '계산'하는 것이 목적이라는 것 기억!
연습문제 3.8
addq %rcx, (%rax)
%rcx의 값과 %rax 메로리 주소에 할당된 값을 더해서 %rax 주소에 저장한다.
D: 0x100
Value: 0x1 + 0xFF = 0x100
subq %rdx, 8(%rax)
8 + %rax(0x100) = 0x108
메모리 0x108에는 0xAB값이 있다.
이 값에서 %rdx(0x3)을 뺀다.(0xAB - 0x3 = 0xA8)
0xA8을 원래 메모리 0x108에 저장한다.
D: 0x108
Value: 0xA8
imulq $16, (%rax,%rdx,8)
0x100 + 8 * 0x3 = 256 + 24 = 280 = 0x118
메모리 주소 0x118의 값은 0x11임
0x11에 16을 곱하면 0x110
D: 0x118
Value: 0x110
incq 16(%rax) (이거 못 풀었음!)
(16바이트 + 0x100) = (0x10 + 0x100) = (0x110)
D: 0x110
Value: 0x14
(16바이트는 16진수로 0x10)
$이 없으면 상수가 아니라 16바이트를 의미
inc는 주어진 오퍼랜드 값을 1만큼 증가시키는 명령어
decq %rcx
%rcx는 그 자체가 0x1이다. 이 값을 1 감소 시키면 0이다.
D: %rcx
Value: 0
subq %rdx,%rax
%rax 값인 0x100에서 %rdx값인 0x3을 빼면
D: %rax
Value: 0xFD
어셈블리어 기본적인 연산은 할 수 있겠다!
연습문제 3.13
해당 인스트럭션 해석 방법 먼저 공부함.
inc comp(data_t a, data_t b) {
return a COMP b;
}a는 %rdi, b는 %rsi에 저장
A.
cmpl %esi, %edi // 내부적으로 %edi - %esi 연산을 수행한 후 플래그 레지스터를 업데이트
// set less는 SF(Sign Flag)와 OF(Over Flag)값이 다를 때, %al 레지스터에 1을 설정함.
setl %al
B.
cmpw %si, %di // if %si >= %di: %al = 1 else 0
// set if grater or equal은 SF와 OF가 같을 때, %al 레지스터에 1을 설정함.
setge %al
C.
cmpq %rsi, %rdi
setne %al //%rsi와 %rdi 값이 같이 않으면 %al 레지스터를 1로 설정함.cmp는 연산 후 결과를 저장하지 않고 EFLAGS 레지스터의 상태 플래그를 자동으로 업데이트한다.
그 후 변경된 플래그 값을 기준으로 set계열의 조건 명령어를 활용할 수 있다.
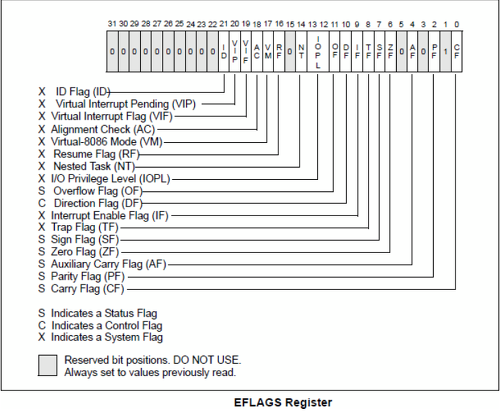
REFLAGS 레지스터
상태 플래그와 제어 플래그를 저장한다.
16비트 아키텍처: FLAGS(16비트)
32비트 아키텍처: EFLAGS(32비트)
64비트 아키텍처: RFLAGS(64비트)
연습문제 3.15
A.
4003fa: 74 02 je XXXXXX
4003fc: ff d0 callq *%rax풀이
je는 다음 인스트럭션 시작 주소를 기준으로 2바이트 앞으로 뛰어야 한다.
따라서 xxxxxx의 값은 4003fc에서 2바이트 건너 뛴 4003fe가 된다.
(왼쪽이 바이트 코드, 오른쪽이 어셈블리 주석)
4003fa: 인스트럭션이 위치한 메모리 주소
74: je 인스트럭션의 오퍼코드
02: 점프할 위치에 대한 오프셋, 현재 주소(정확히는 점프 인스트럭션의 다음 인스트럭션을 기준으로)에서 2바이트 다음 위치로 점프
je XXXXXX: Zero Flag(ZF)가 1(set)일 때, 지정된 주소로 점프
je명령어는 해당 명령어가 끝나는 지점(다음 명령어 시작점)에서 XXXXXX으로 점프하라는 의미
x86아키텍처에서 점프 인스트럭션 오프셋은 해당 점프 인스트럭션 다음 인스트럭션의 주소를 기준으로 함.
이러한 방식은 인스트럭션을 가져온 후 프로그램 카운터를 즉시 다음 인스트럭션 주소로 업데이트 했던 관습에서 가져 옴.
B.
40042f: 74 f4 je XXXXXX
400431: 5d pop %rbp풀이
je는 오퍼랜드를 signed로 해석한다.
f4는 바이너리로 표현하면 1111 0100이며, 최상위 비트가 1이므로 음수이다.
1의 보수로 반전 시키면 0000 1011이며, 2의 보수로 나타내기 위해 1을 더하면
0000 1100이며 이 값은 12이며, 원래 바이너리 부호를 반영하여 -12이다.
점프를 해야 하는 위치를 점프 인스트럭션 다음 인스트럭션 주소인 0x400431에서 -12를 하면 된다. 그 값은 0x400425이다.
je는 ZF가 1이면(즉, 직전 연산의 값이 0이거나 cmp가 0이면) 점프한다. 즉, 조건문을 구현할 때 비교 후 참이면 해당 조건문이 실행되는 방식에서 적용될 수 있다.
C.
이거 혼자 풀어서 맞음!
// 문제
XXXXXX: 77 02 ja 400547
XXXXXX: 5d POP %rbp
// 정답
400543: 77 02 ja 400547
400545: 5d POP %rbpja 인스트럭션은 2바이트를 차지한다.
바이트 코드에서 FF와 같이 나오는 숫자를 무조건 signed로 해석하는건가?
아님! 바이트 코드 자체가 signed, unsigned를 결정하는 건 아님!
인스트럭션에 따라 오퍼랜드의 값을 signed로 해석할지 unsigned로 해석할지가 달라지는 것!
D.
4005e8: e9 73 ff ff ff jmpq XXXXXX
4005ed: 90 nop풀이
리틀 엔디안 방식이므로 오프셋은 FF FF FF 73
1의 보수를 구하면 00 00 00 8C
2의 보수를 구하면 00 00 00 8D
10진수로 변환하면 141, 부호를 반영하면 -141
다음 인스트럭션 4005ed에서 -141을 하면 점프 주소가 400560이 나옴.
리틀 엔디안 vs 빅 엔디안
둘 다 바이트 순서를 나타내는 용어이다. 비트 순서가 아닌 것 주의!
빅 엔디안은 높은 주소에 높은 중요도를 가진 바이트가 저장된다.
-> 메모리 시작 주소에는 데이터 앞쪽 바이트가 있다.
리틀 엔디안은 낮은 주소에 높은 중요도를 가진 바이트가 저장된다.
-> 메모리 시작 주소에는 데이터의 뒤쪽 바이트가 있다.(역순)
x86-64 아키텍처는 리틀 엔디안을 사용한다.
리틀 엔디안이 좋은 점은 하위 비트가 필요할 때 시작 주소부터 바로 접근해서 가져올 수 있음.
확장성 측면에서 간단함. 비트를 확장하려면 추가 바이트를 메모리 뒷부분에 추가하면 됨.(빅 엔디안은 기존 값을 메모리 뒤로 옮기고, 나머지를 앞쪽에 추가해야 함.)
연습문제 3.16
c코드와 어셈블리 매칭이 안 돼서 이해에 2시간 이상 소요함.
왜 jle로 하는지 모르겠음. (jge아닌가?)
void cond(short a, short *p)
{
if (a && *p < a)
*p = a;
}
// a in %rdi, p in %rsi
// cond:
// testq %rdi, %rdi ; a값이 0이 아닌지 체크
// je .L1 ; a값이 0이면 L1로 점프(함수 종료)
// cmpq (%rsi), %rdi ; *p와 a비교
// jge .L1 ; *p >= a 인지 체크해서 충족하면 L1로 점프(함수 종료) 교재에서는 이 부분이 jge가 아니라 jle이다.
// movq %rdi, (%rsi) ; a의 값을 *p로 할당
// .L1:
// rep; ret ; 함수 종료3주차 퀴즈 복기
- 스택에 대한 피상적인 정의만 알고 있었음. 스택 프레임 구성 요소 정확히 공부하기
- LCS 경로 역추적 하는 것 정확히 모르고 있음.
- 플로이드 와샬 이행적 폐쇄 개념 모름
- 꼬리 재귀 최적화는 들어본 적도 없음 (교재에 없는데 중요해서 출제했다고 하심)
- 동적 프로그래밍에서 상향식과 하향식 차이 정확히 모름
동적 프로그래밍: 복잡한 문제를 하위 문제로 나누어 해결하고, 그 해결책을 저장해서 최종 문제의 해답을 구하는데 사용하는 알고리즘 설계 기법
상향식: 가장 작은 문제부터 시작하여 큰 문제의 해답을 구하는 방식(작은 문제 답 구하고 점점 나아감)
하향식: 큰 문제에서 시작해서 아직 계산되지 않은 하위 문제를 재귀적으로 호출하며 해결(큰 문제 답이 안 구해진 상황에서 큰 문제를 냅두고 더 작은 문제를 풀어 나감)
메모이제이션 vs 타뷸레이션
메모이제이션은 부분 문제에 대한 해결 결과를 저장해놓는 개념이며, DP하향식에서 사용한다.
특정 부분 문제에 대한 해를 저장하고, 다른 동일한 부분 문제에서 사용한다.
-> 필요한 것만 계산해서 저장해 놓고 씀.
타뷸레이션은 전체 문제에 대한 부분의 문제를 순차적으로 결과를 저장하기 위한 표를 작성해 나가는 방식이며, DP상향식에서 사용한다.
상향식으로 부분 문제를 해결해 나갈 때 표를 작성해 나가면서 작성된 표를 다른 부분 문제를 해결할 때 사용한다.
-> 모든 부분 문제의 답을 순차적으로 계산해서 표로 정리함.
메모이제이션은 필요할 때 부분 문제의 해결을 저장하는 방식이며, 타뷸레이션은 모든 부분 문제의 해결을 순차적으로 표 형식으로 저장하는 방식이다. (GPT)
아직 안 푼 문제
3.9 ~ 3.31
