[크래프톤 정글 3기] 12/2(토) TIL

ClassBinu·2023년 12월 2일

크래프톤 정글 3기 TIL

목록 보기

49/120

08:40 입실
핀토스 MLFQ 완성하고 발표까지 준비하기

Pintos

load_avg

평균 부하를 나타낸다.
시스템 전체에서 1개의 값이다.

실행 중이거나 대기 중인 스레드들의 평균 수를 나타낸다.
이 값을 매 초마다 업데이트되며, 시스템 부하에 따라 변한다.

load_avg = (59/60) * load_avg + (1/60) * ready_threads
현재까지의 부하의 59/60을 반영하고,
새롭게 반영될 부하(스레드 수)를 1/60 만큼 반영한다.

recent_cpu

특정 스레드가 최근에(과거에) 얼마나 많은 CPU를 사용했는지 나타내는 값
각 스레드마다 가지고 있는 값이다.

해당 스레드가 얼마나 바쁜지 평가하는 요소.
-> 스레드가 CPU를 많이 점슈할 수록 이 값은 증가한다.

우선순위 계산에 반영한다.
recent_cpu가 높으면 cpu를 과도하게 사용한 것이므로, 스레드의 우선 순위를 낮춘다.

recent_cpu = (2 * load_avg) / (2 * load_avg + 1) * recent_cpu + nice

recent_cpu가 업데이트되는 시점은 다음과 같다.
1. 매 타이머 틱마다 1씩 증가

priority

각 스레드가 가지고 있는 우선순위 값

0부터 64까지의 값이 있으며 나이스 값(-20 ~ 20)에 따라 계산된다.
recent_cpu가 높으면, nice가 높으면 우선순위는 낮아진다.
4틱마다 우선순위를 재조정한다.

priority = PRI_MAX - (recent_cpu / 4) - (nice * 2)

재계산 시점

매틱마다 recent_cpu를 +1한다.
4틱마다 priority 재계산한다.
100틱마다 시스템의 load_avg를 재계산한다.
100틱마다 전체 스레드의 priority를 재계산한다.

1차 구현

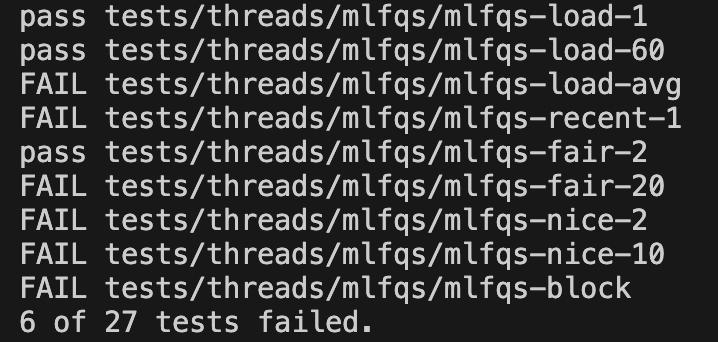
2차 구현

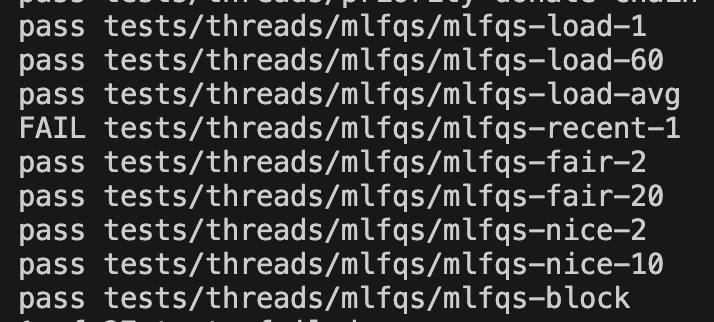
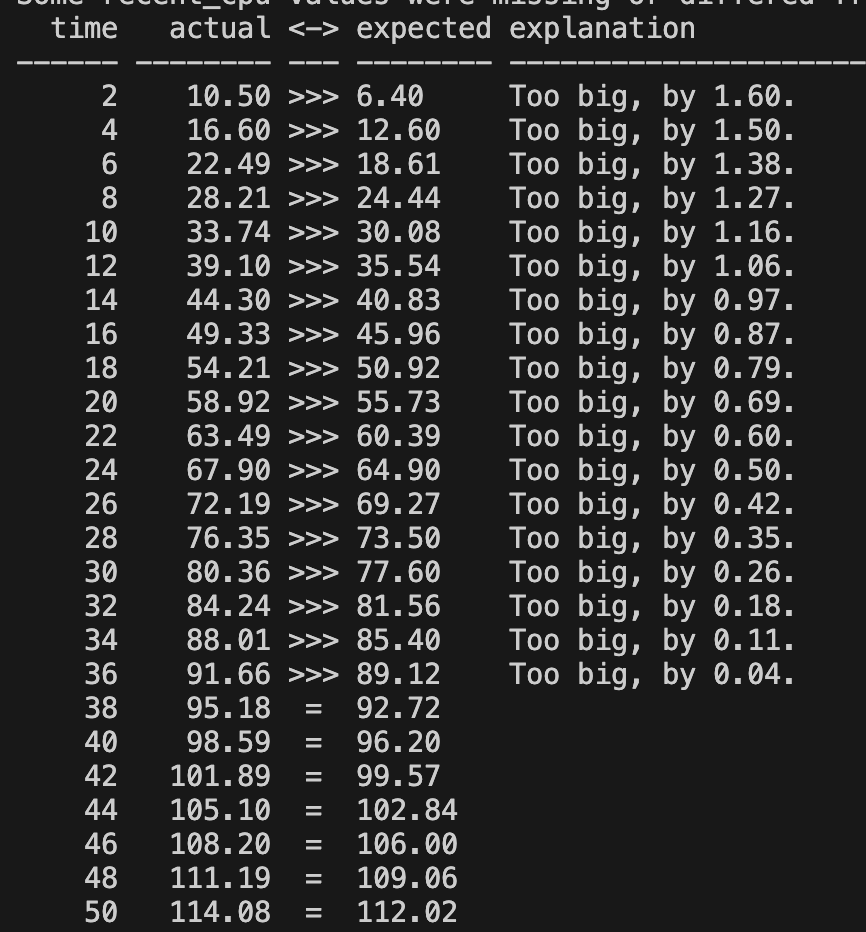
3차 구현

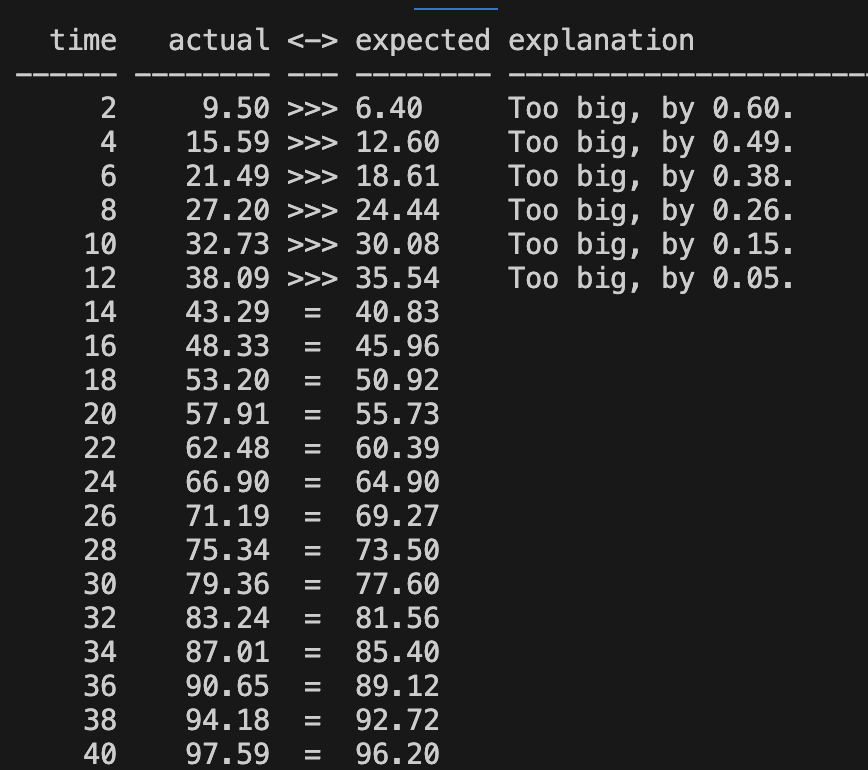
recent_cpu 반올림 코드를 없애니까 오류 케이스가 조금 줄어 들었음.

4차 구현

void mlfqs_recalc(void)
{
	struct thread *cur = thread_current();
	struct list_elem *e;

	// 현재 스레드의 recent_cpu와 priority 재계산
	if (cur != idle_thread)
	{
		mlfqs_recent_cpu(cur);
		mlfqs_priority(cur);
	}

	for (e = list_begin(&ready_list); e != list_end(&ready_list); e = list_next(e))
	{
		struct thread *t = list_entry(e, struct thread, elem);
		if (t != idle_thread)
		{
			mlfqs_recent_cpu(t); // recent_cpu 재계산
			mlfqs_priority(t);	 // priority 재계산
		}
	}

	for (e = list_begin(&sleep_list); e != list_end(&sleep_list); e = list_next(e))
	{
		struct thread *t = list_entry(e, struct thread, elem);
		if (t != idle_thread)
		{
			mlfqs_recent_cpu(t); // recent_cpu 재계산
			mlfqs_priority(t);	 // priority 재계산
		}
	}
}