[계산사진학] Edge Aware Image Filtering - Guided Filtering

Edge aware filter 중 가장 대표적인 bilateral filter를 알아보았다. 이번에는 다른 방법인 guided image filtering에 대해서 알아보려고 한다. Guided filter는 마찬가지로 edge aware filter이며 bilateral filter와 비슷한 결과를 만들어낸다. 하지만 guided filter는 bilateral filter보다 훨씬 빠른 속도로 동작한다. 이것이 guided filter를 사용하는 이유가 된다.

Guided Filter

Guided filter는 input 이미지 $p$와 guide 이미지 $I$를 필요로 한다. Bilateral filter와는 다르게 guide 이미지를 추가로 사용하게 된다. 여기서 guide 이미지 $I$는 input 이미지 $p$가 될 수도 있다. 즉, guided filtering 시 input 이미지를 guide 이미지로 사용할 수 있다. Guide 이미지는 input 이미지와는 다른 intensity 값들을 가지고 있다. 그러나 guide 이미지는 input 이미지와 edge 정보를 공유하게 된다. Input 이미지는 edge와 더불어 high frequency component의 noise가 많이 있다. 이러한 두 종류의 이미지로부터 output 이미지 $q$를 만들어내게 된다. Guided filtering은 $I$에 있는 edge 정보를 기반으로 $p$에 있는 noise를 제거하게 된다. 그럼 이제 guided filter가 어떻게 동작하는지 알아보도록 하자.
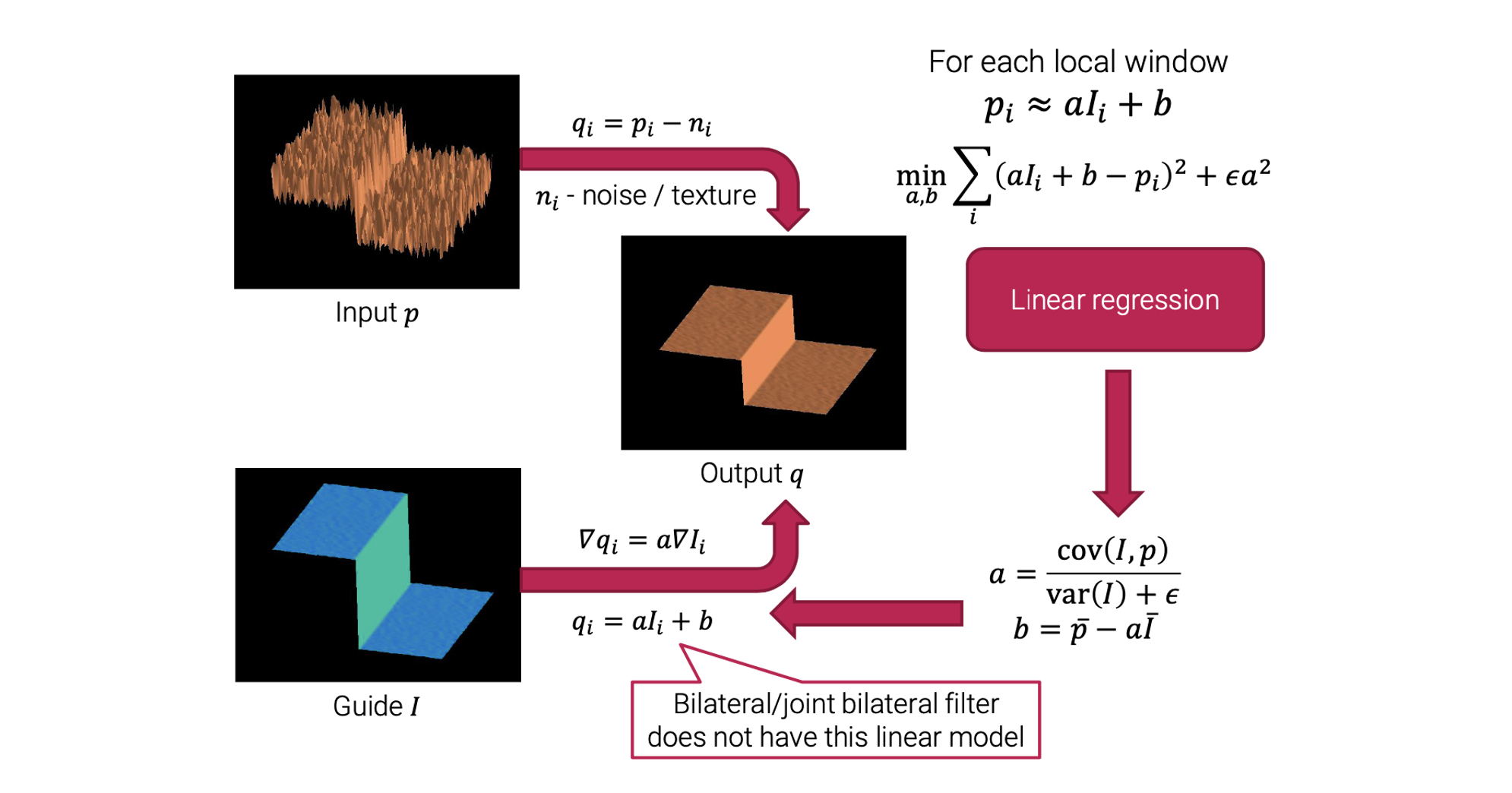가장 먼저 guided filtering은 이미지 patch로부터 동작하게 된다. 위에서 input $p$는 전체 이미지를 나타내는 것은 아니다. 이는 I로부터 단지 하나의 patch에 대응되는 일부분이다. 그리고 이는 똑같이 guide $I$에 대응되게 된다. 그래서 우리는 $p$와 $I$로 부터 2개의 patch 추출하게 되는 것이다. 그리고 이 patch들은 같은 위치로부터 추출되었다. 그리고 output patch $q_i$는 $p_i - n_i$이 된다. 여기서, $n$은 noise component이다. 그리고 $i$는 patch index이다. Guided filter는 guide patch $I$에 linear transformation을 적용하여 ouput patch $q$를 만들게 된다. Guide $I$는 noise가 없지만 input $p$와 edge를 공유할 수 있어서 우리는 $a$와 $b$에 적당한 값을 쉽게 정의할 수 있다. 그리고 이를 통해서 $I$를 transformation 시켜 noise가 없는 ouput $q$를 얻을 수 있다. 이것이 guided filtering의 간단한 진행 방식이다.

각각의 이미지 patch, 혹은 local window마다 input $p$는 guide 이미지와 비슷하게 된다. 그래서 이러한 relation으로부터 least square problem을 만들 수 있다. Input과 guide의 차이를 최소화 해야 하며, 이때 guide 이미지나 input 이미지가 단순히 constant patch라면 여러개의 solution이 존재할 수 있게 된다. Constant patch는 구조적으로 아무것도 존재하지 않는다. 이를 피하기 위해서 우리는 $a$를 가지는 solution을 찾기 위해서 regularization 항을 가지게 된다. Parameter $a, b$는 이 식을 풀게 되면 쉽게 구할 수가 있다.

위에서 보다시피 우리는 guide 이미지가 noise를 가지고 있지 않다고 가정했다. 그리고 이는 사실은 비현실적이다. 그러나, 이를 설명하는 저자는 guided filter가 noise가 없는 giude 이미지로 noise를 없앨 수 있다는 것을 보여줬다. 어떻게 이게 가능했을까? Denoising에 대해서 더 나은 이해를 위해서 다른 예시를 보도록 하자.

먼저 간단하게 guide 이미지 $I$가 input 이미지 $p$와 같다고 가정한다. 그래서 이 예시에서는 input 이미지를 guide 이미지로 생각할 것이다. 그래서 추가적으로 noise가 없는 guide 이미지는 없다고 생각할 것이고, 오직 input 이미지만을 guide 이미지로 사용할 것이다. 이는 전형적인 상황이 될 것이다. 그러면, 이제 각각의 local window에 대해서 input 이미지 patch와 output 이미지 patch 사이에 다음의 relation을 가지도록 할 것이다.

Guided filter는 filtering의 결과로 $q$를 얻기 위해서 guide patch $I$를 transform시킨다. 우리는 input을 guide로 사용했기 때문에 위와 같은 relation을 성립할 수 있는 것이다. 여기에는 2개의 coefficient $a, b$가 있다. $a$는 contrast와 관련이 있는 coefficient이고, $b$는 average intensity와 관련이 있다. 우리는 parameter $a$를 조절하여 이 patch의 contrast를 바꿀 수 있고, parameter $b$를 조절하여 이 patch의 average intensity를 조절할 수 있다.

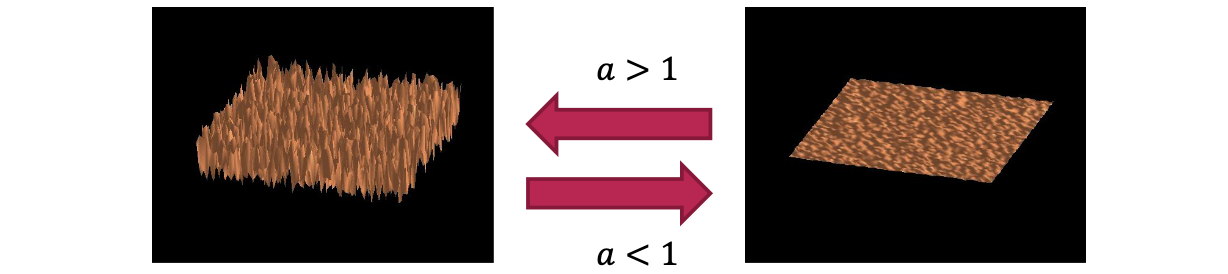그러면 이제 2가지 경우를 생각해보자. $a$가 1보다 크게 되면, 우리는 input patch에서의 noise와 같이 small variation을 증대할 수 있다. 그리고 이때 parameter $b$는 자동적으로 $a$와 관련해서 결정되게 된다. 그 이유는 $b = q_i - ap_i$로 계산이 가능하기 때문이다. 반대로, $a$가 1보다 작아지게 되면 noise와 같은 small variation을 억제하게 된다. 왜냐하면 input 이미지 patch에 대해서 contrast를 줄이기 때문이다.

그래서 guided image filtering에서 우리의 목적은 $a$와 $b$를 찾는 것이다. 그리고 이들을 찾기 위해서 다음과 같은 least square problem을 풀어야 한다.
Left term은 input 이미지와 output 이미지로부터 유도한 것이다. 그리고 right term과 regularization term은 작은 값의 $a$를 선호하게 된다. $\epsilon$은 regularization term의 strength를 조절하게 된다. 그리고 만약 $\epsilon$이 크다면, 그 결과 $a$는 작아지게 될 것이고, $a$가 작다는 것은 noise가 억제될 것이라는 것을 의미하게 된다. 다음과 같이 noise가 있는 smooth area를 생각해보자.
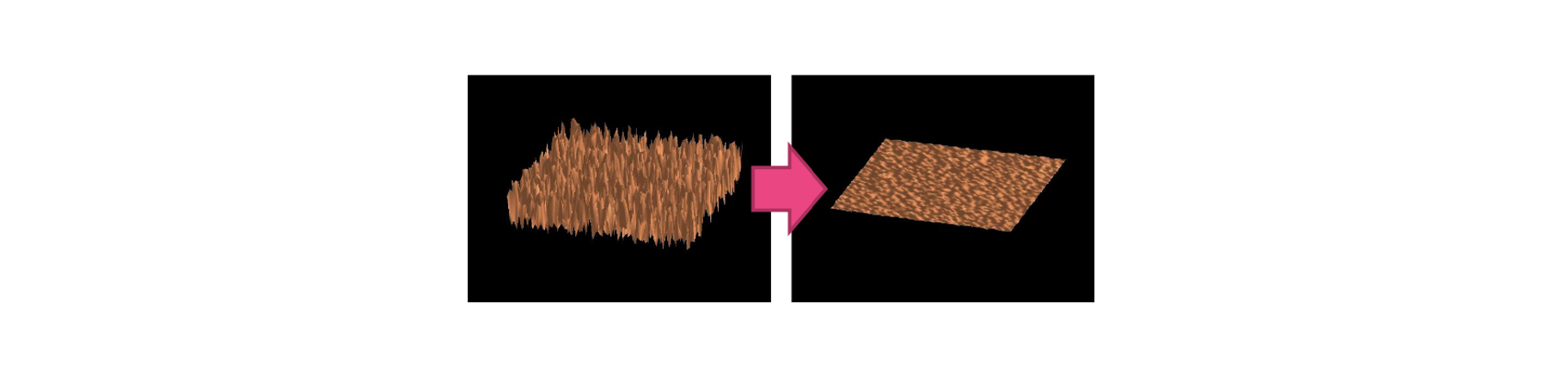Denoising 후에는 오른쪽과 같이 noise가 사라진 smooth한 결과가 나올 것이다. 그래서 이러한 이미지 area에 대해서 $\epsilon$이 커져서 $a$가 작아지게 되어 0에 수렴하면 $b$는 patch에 대해서 average intensity에 수렴하게 될 것이다. 그래서 이러한 경우에 대해서는 이것이 가장 이상적인 해답이 될 것이다. 결과적으로 우리는 위와 같은 area에 대해서는 denoise patch를 얻게 된 것이고, 만약 다음과 같이 강한 edge가 있는 경우에는 이야기가 조금 달라지게 된다.
이렇게 edge가 강하게 존재할 때는, $a$가 아주 작아지는 것은 불가능하다. $a$가 작아지게 되면 첫번째 term에 대해서 더 큰 data error를 발생시키게 된다. 그래서 $a$가 0에 수렴하게 되면 constrast를 줄이게 될 것이고 edge strength마저 줄이게 될 것이다. 그리하여 $a$가 0에 수렴하면 data error가 더 커지게 될 것이다. 그래서 이러한 경우 least square problem을 풀게 되면 첫번째 term에 대해서 error를 줄이기 위해서 $a$는 1에 수렴하게 되고, $b$는 0에 수렴하게 될 것이다.

Guided filter는 input patch의 구조에 따라서 coefficient $a, b$를 예측하게 된다. 만약에 input patch가 많은 구조와 edge, 그리고 큰 contrast를 가지게 된다면 coefficient $a, b$는 0과 1에 따로 수렴하게 될 것이다. 만약에 input patch가 noise를 가지면서 smooth하다면, coefficient $a$는 0에 수렴할 것이고, $b$는 input patch의 average intensity에 수렴하게 될 것이다. 즉, parameter들은 input 이미지 patch의 구조에 따라서 예측이 될 것이다.

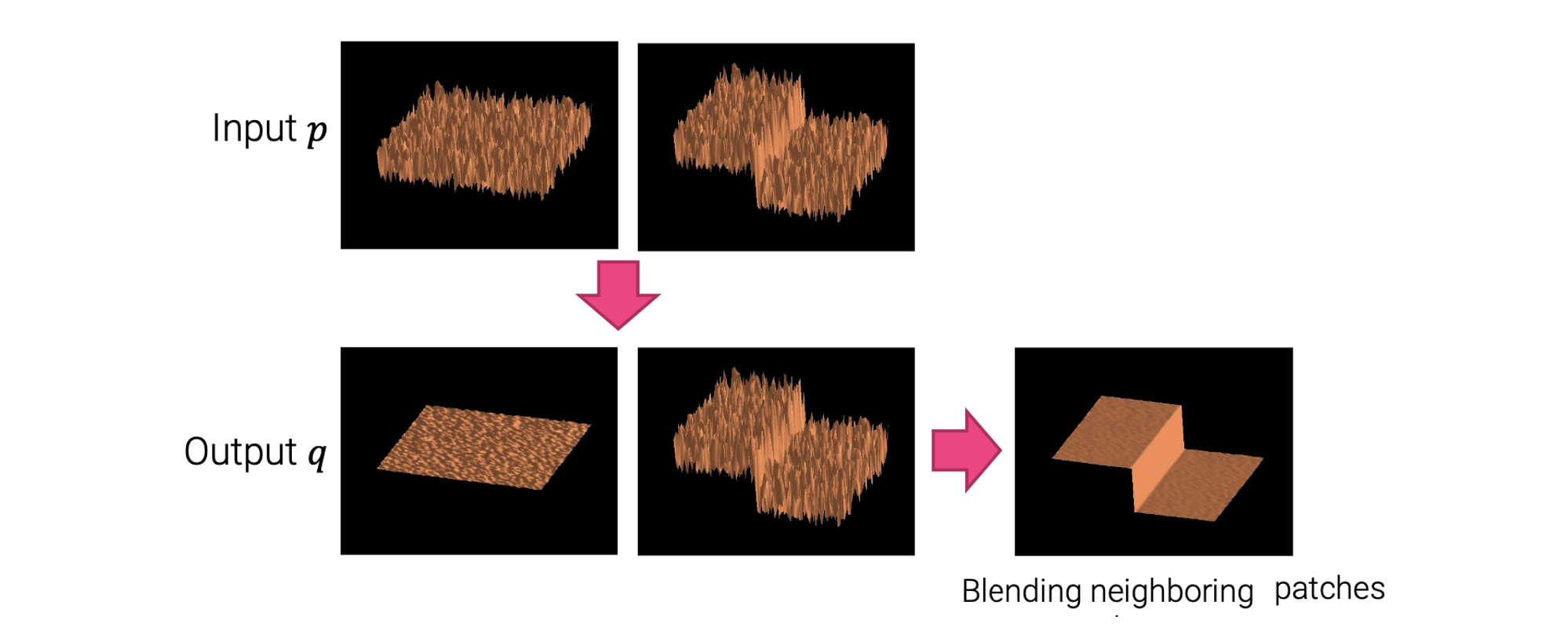그리고 guided image filtering에서 이미지는 서로 겹쳐지는 input patch로 나눠지게 된다. 단지 나열된 연속적인 patch로 나눠지는 것이 아닌, 서로서로 겹쳐지는 형태로 나눠지게 된다. 그래서 만약 이미지에서 하나의 픽셀이 있고 크기가 7인 kernel이 있다고 했을 때, 해당하는 이 픽셀을 포함하는 patch는 총 49개가 되는 것이다. 이 49개의 patch들에 대해서 guided filter는 coefficient를 찾을 수 있다. 그리고 모든 $a, b$는 각 patch마다 다르게 예측이 될 것이고, 이들은 이후에 함께 blending 될 것이다. 이러한 방식 덕분에 edge component에 대해서 noise를 제거하지 못하더라도 overlap 된 다른 patch 덕분에 edge를 살리면서 noise를 제거할 수 있게 되었다. 이것이 바로 guided image filter가 image denoising을 하기 위해서 동작하는 방식이다.

Guided filter는 마찬가지로 2개의 parameter를 가지게 된다. 하나는 patch의 크기이고, 다른 하나는 regularization term에서 strength를 조절할 수 있는 $\epsilon$이다. $\epsilon$는 strong denoising을 의미하며, 이 2개의 parameter는 bilateral filter의 2개의 parameter들과 유사한 역할을 하게 된다.
Patch의 크기는 bilateral filter에서 spatial weighting function의 $\sigma_s$와 유사한 역할을 한다. 그리고 $\epsilon$은 bilateral filter에서 intensity range weighting function의 $\sigma_r$과 유사한 역할을 한다. 그래서 이 2개의 parameter들을 조절함에 따라 서로 다른 denoised 이미지를 얻을 수가 있다. $\epsilon$의 크기를 키울수록 더 강하게 denoising을 진행하게 된다.

그리고 결과를 보다시피 guided filter도 edge들을 효과적으로 보존하게 된다. 왜냐하면 guided image filter가 coefficient $a, b$를 찾는데, 이들은 원래의 이미지에서 구조적인 특징이나 edge들을 보존하기 때문이다.

Fast and Simple

Guided filter의 장점으로는 빠른 속도로 동작한다는 점에 있다. 코드만 봐도 몇 줄 안되고 그로인하여 실행 속도가 빠른 편에 속하게 된다. Guided filtering을 진행할 때, input 이미지에 대해서 모든 patch로부터 parameter $a, b$를 예측하도록 해야한다. 이렇게만 보면 조금 복잡해 보일 수 있다. 그러나 이러한 연산은 simple mean filtering을 사용함에 따라 매우 효과적으로 수행 되는 부분이다.
위의 코드는 guided filter에 대한 pseudo code이다. Guided filtering을 진행하기 위해서는 각각의 patch마다 $I$와 $p$ 사이의 covariance를 구해줘야만 한다. 그리고 $I$에 대해서 variance와 mean intensity도 구해줘야 한다. 매 patch마다 이러한 것들을 구한다고 했을 때, 조금 복잡해 보일 수 있다. 그러나 실제로는 mean filtering의 combination을 통해서 이는 굉장히 쉽게 구해질 수 있는 부분이다. 여기서 mean filtering은 box filtering의 다른 이름이다. Mean filtering을 convolution operation으로 구하게 된다. 그리고 매 patch마다 variance도 mean filter와 pixel-wise operation을 통해서 쉽게 구할 수 있다. Mean filtering은 "summed area table" 알고리즘에 의해서 더 빨라질 수 있다.

Summed Area Table

Summed area table은 mean filtering 알고리즘을 더욱 가속화 시켜줄 수 있다. 우리가 summed area table 알고리즘에서 구하고 싶은 문제는 어떻게 $k\times k$ patch들의 평균을 구하는지이다. 이 문제를 해결하기 위한 방법은 몇가지가 존재한다.
Option 1은 단순히 convolution operation을 진행하는 것이다. 그리고 이렇게 했을 때, time complexity는 $O(k^2N)$이다. 아마도 Fourier transform을 사용하면 convolution operation을 가속화 할 수 있게 된다. 그래서 option 2는 FFT를 이용하는 것으로 이때의 time complexity는 $O(NlogN)$이 된다. Spatial domain에서의 convolution operation은 frequency domaind에서의 pixel-wise multiplication과 같다. 이때 각각의 time complexity는 $O(N)$이고, Fourier transform의 time complexity는 $O(NlogN)$이다. 그래서 total time complexity는 $O(NlogN)$이 된다. 마지막 option은 바로 summed area table을 사용하는 것이다. 이 알고리즘은 굉장히 빠르고, time complexity는 $O(N)$이다. 그렇다면 어떻게 이렇게 빠른 속도가 가능한 것일까?
가장 먼저 cumulative sum을 horizontal 방향으로 구해준다. 그리고 이렇게 구해준 sum들로 table을 대체하고, 이로부터 다시 vertical 방향으로 cumulative sum을 구해준다. 그리고 이 sum들로 다시 table을 만들어주면, 이 table을 summed area table이라고 부르는 것이다. 그렇다면 이 table은 무엇을 의미하는 것일까?
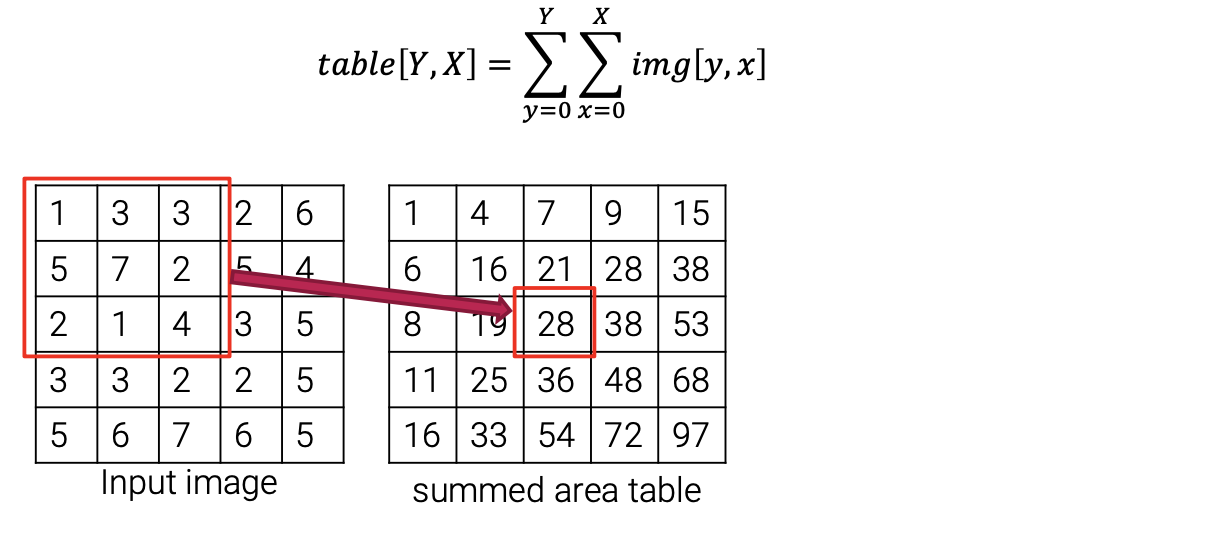Table에 있는 각각의 element는 위와 같이 시작점부터 원래의 위치까지 있던 값들의 합을 나타내게 된다. 그래서 중간에 있는 28은 원래의 이미지에 있는 9개의 값들의 합과 같아지게 된다. 이렇게 table을 만들게 되면, 우리는 각 이미지 patch의 평균을 다음과 같이 값들의 조합으로 쉽게 구할 수 있다.
이러한 summed area table을 이용하면 mean filtering operation과 같은 방식에서 속도적인 측면을 해결하게 된다.

Applications

그럼 이제 guided image filter가 적용되는 분야들을 살펴보도록 하자. Bilateral filter와 다른 lowpass filter와 비슷하게 guided filter은 denoising과 같은 여러 이미지 프로세싱 task에 사용이 된다.

Detail Enhancement

Detail enhancement는 다른 lowpass filter를 사용하는 unsharp masking의 일종으로 간주되어진다. Detail enhancement는 기본적으로 unsharp masking과 비슷하다. 그래서 우리가 하기를 원하는 것은 다음과 같다.
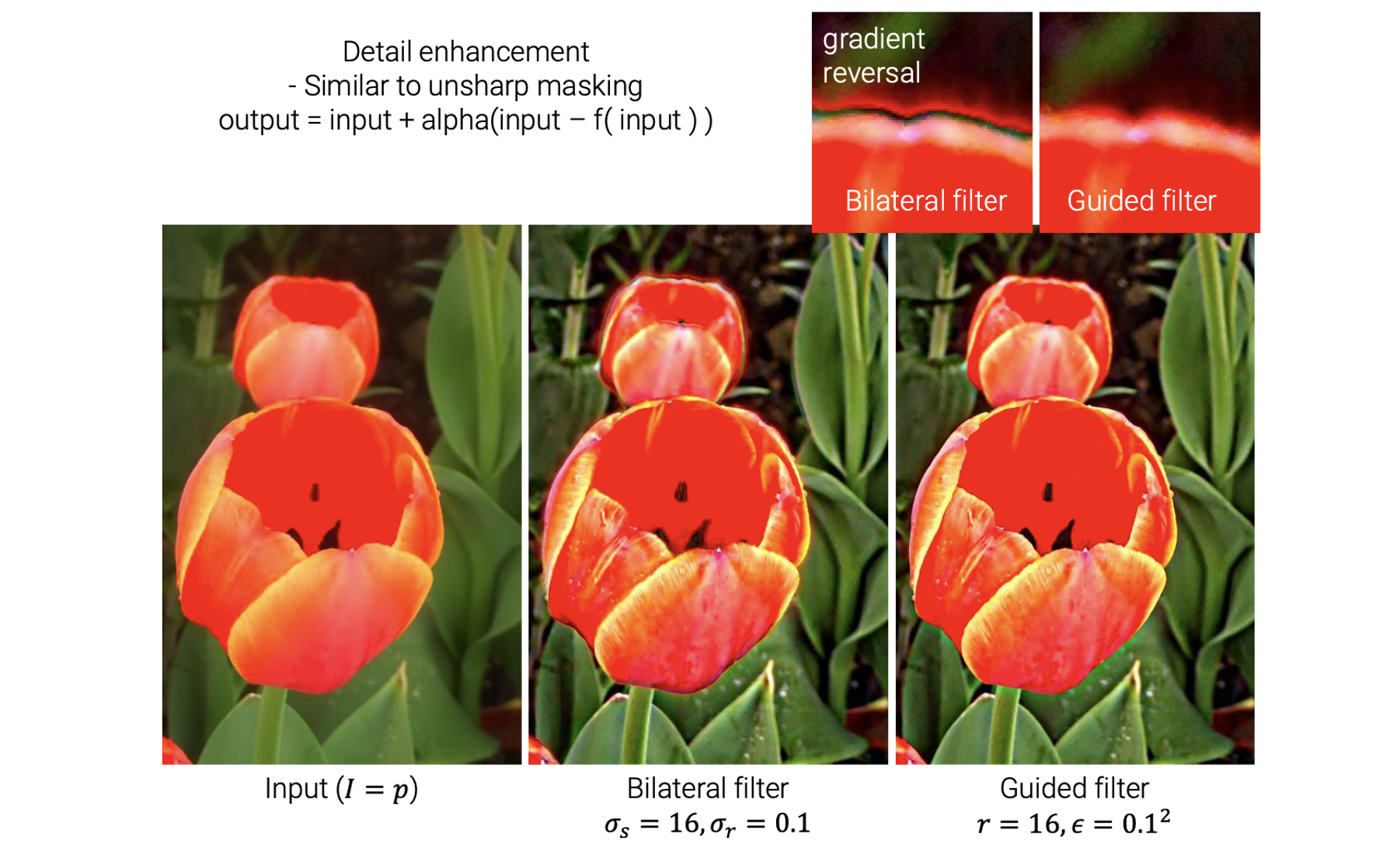위의 예시 이미지는 많은 디테일을 가지고 있다. 하지만 디테일들이 부각되어 있지는 않다. 그래서 우리는 이러한 디테일적인 부분들을 부각시켜주도록 이미지를 조작하도록 할 것이다. 이러한 경우에 detail enhancement를 사용하는 것이다. Detail enhancement를 적용한 후에는 오른쪽의 이미지와 같이 부각된 디테일이 담긴 이미지를 볼 수가 있다. 그리고 이러한 operation은 다음과 같은 방식으로 진행된다.

우선, guided image filter를 이용해서 low frequency component를 추출하고, 이를 이용해서 input 이미지로부터 high frequency component를 추출하게 된다. 그리고 이 high frequency component를 다시 input 이미지에 더해주게 되면 결과적으로 filtering 된 이미지가 만들어진다. 사실 이러한 과정은 bilateral filter에서도 마찬가지이다. 그리고 이미지를 서로 다른 frequency component로 분해하기 위해서 사용되는 lowpass filter로는 어떠한 것을 사용해도 된다.

사실 bilateral filter와 guided filter는 모두 edge aware filter다. 위의 이미지는 guided filter의 논문으로 부터 발췌된 이미지이며, 이 이미지가 보여주고자 하는 것은 gudied filter가 사실 이미지로부터 strong edge들을 더 잘 보존한다는 것이다.

Guided Filter(con't)

지금까지는 input 이미지를 guide 이미지와 같다고 간주했다. 그렇다면 만약 다른 경우에는 어떠할까? Input 이미지와는 다른 이미지를 guide 이미지로 사용할 수 있다. 그리고 이러한 방식은 여러 application에도 적용이 된다. 만약 $I \neq p$ 라면, guide filter는 joint bilateral filter와 비슷하게 동작할 것이다. 이러한 경우에 각각의 local window에 대해서 output patch $q$를 다음과 같이 model할 수 있다.

그리고 parameter $a, b$는 다음과 같은 relation에 의해서 결정된다.

직관적으로, 우리는 input $p$를 patch들로 부터 contrast와 mean intensity를 조절해서 guide $I$로부터 reconstruct하고 싶다.

Flash/No-Flash Denoising

이렇게 guided filter를 이용하면 joint bilateral filter와 비슷한 역할을 수행할 수 있다.
우리는 flash 이미지를 guide 이미지로 사용하여 no-flash 이미지의 noise를 제거할 수 있다. Flash 이미지는 noise가 존재하지 않는다. 그래서 이 이미지를 guide 이미지로 사용할 수 있는 것이다. Guide 이미지에서 각각의 patch마다 linear transformation을 진행해주면 transformed patch가 최대한 input patch $p$와 비슷하게 보일 것이다.
그리고 위의 이미지는 joint bilateral filter를 이용했을 때 결과이다.
그리고 위의 이미지는 guided filter를 이용했을 때 결과이다. 눈으로 보다시피 결과가 비슷하게 나온 것을 볼 수 있다. 그래서 성공적으로 denoising을 했다고 볼 수 있다. 이는 매우 전형적이고 직관적인 예시들이다.

Feathering(Alpha-Matting)

이번에는 다른 예시를 볼 것이다.
우리가 하고 싶은 것은 오직 foreground object를 포함하는 foreground pixel들만을 추출하는 것이다. 이러한 방식을 alpha-matting이라고 한다. 이를 위해서 원본 이미지를 guide 이미지로 사용할 것이다. 그리고 rough한 binary mask를 만들 것이다. Binary mask는 어떠한 pixel이 foreground object에 속하는지 보여줄 수 있다. 하지만 이는 rough한 mask이기 때문에 정확하지는 않다. 그래서 이 이미지를 input $p$로 사용하여 guided filtering을 진행시킬 것이다. 그 결과 foreground object와 굉장히 유사하게 mask가 생성되었다. 이것이 가능한 이유는 guided image filter가 guide 이미지를 기반으로 input 이미지를 생성하기 때문이다. 우리는 guide 이미지로 edge 정보가 많은 이미지를 사용했다. 그렇기 때문에 guided filter가 guide 이미지 $I$의 patch들로부터 linearly transformation을 진행하여 input 이미지 $p$를 복원한 것이다.

Haze Removal

Guided filter는 haze removal에도 사용이 된다. 왼쪽에 안개가 자욱한 도시 이미지가 있다. 이 이미지를 guide 이미지로 하여 중간의 이미지를 복원하여 오른쪽의 결과를 만들어냈다.

이렇게 edge aware filter의 두 종류를 모두 알아보았다. 둘 다 edge는 보존하면서 작은 크기의 high frequency noise들을 제거할 수 있다. 이들은 모두 graphics와 vision 분야에 두루 적용되어 사용되고 있다.