[계산사진학] Image Alignment - Feature-Based Alignment

Feature-Based Alignment

Feature-based alginment의 전반적인 과정은 다음과 같다.
우리가 정렬하고 싶은 2개의 image가 주어졌을 때, 가장 먼저 중요한 feature point들에 대해서 찾아야 한다. Feature point는 interst point라고도 한다.
구체적으로 각각의 image로부터 독립적으로 feature point들을 찾아서 2개의 image로부터 feature point들에 대한 2개의 independent set을 만들게 된다.
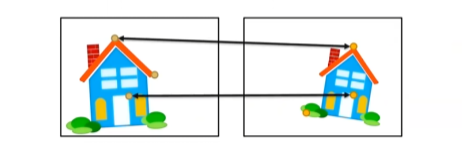그리고는 image들 사이의 feature point들을 matching하여 feature point들의 matched pair로부터 image transformation을 계산해준다.

여기서 보았듯이 feature-based alignment에서 feature point detection과 matching은 image alignment에 있어 중요한 step들이다. 그래서 이것이 왜 feature-based alginment라고 불리는 이유이다. 다음 내용부터는 각 step마다 더 깊게 이야기를 해보고자 한다.

Feature Detection

첫번째 step은 feature detection이다. 이 step의 목표는 image로부터 feature point들을 찾는 것이다.
이 예시에서 작은 point들은 각각의 image로부터 검출된 feature point들이다. 이 step에서는 특히 다른 image에서도 찾을 수 있는 point들에 대해서 관심을 가지게 된다. 그리고 이 point들은 정확하고 신뢰할 수 있다. 지금부터는 이 property들을 자세하게 보도록 하자.

1. Found in other images : 우리는 image가 예를 들어 edge나 corner와 같이 흔히 자연스럽게 가지고 있는 feature point를 원한다.
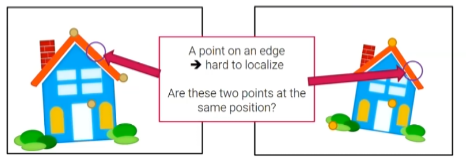
2. Found precisely - well localized : 우리가 image로부터 특정 edge 위에 있는 2개의 point들을 검출했다고 해보자. 이는 이 feature point가 같은 위치에 있는지 아닌지에 대해서 말하기 어렵다. 왜냐하면 edge위에 존재하는 다른 point들이 겉으로보기에는 거의 똑같기 때문이다. 반면에 corner은 localize 하기에 더 쉬운 특징이 있다. 그래서 corner에 있는 point들에 대해서는 같은 위치에 있다고 말할 수 있다. 그래서 이 point들은 matching 될 수가 있는 것이다.
3. Found reliably - well matched : 우리는 feature point들이 신뢰할 수 있기를 원한다. 예를 들어서 만약 low contrast를 가지는 매우 어두운 image를 가지고 있다고 해보자. 이러한 image에서는 noise나 lighting condition에 따라서 corner와 같은 image feature들이 검출이 되거나 되지 않을 수가 있다. 그래서 feature detection을 신뢰할 수 없을 것이다.

그래서 어떠한 종류의 point가 좋은 feature가 되는 것일까? 일반적으로 개체의 corner는 이러한 3가지 필요조건을 만족하는 매우 좋은 feature에 해당한다. 많은 feature point detection algorithm들에서 corner를 feature point로 많이 사용하곤 한다.

Harris Corner Detector

Feature detection을 위해서 사용 가능한 feature detector들이 많이 존재한다. 이러한 많은 detector들 중에서 Harris corner detector에 대해서 간단하게 알아보려고 한다.
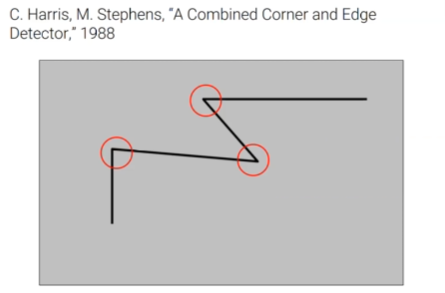이름에서 보았듯이 Harris corner detector는 image로부터 개체들의 corner를 feature point로 검출하게 된다.

Corner Detection

Corner을 검출하기 위해서 Harris corner detector는 다음의 key property에 따른다.
Corner 주변 지역에서 image gradient는 2개 혹은 더 지배적인 방향을 가지게 된다.

Corner Detection: The Basics

Corner detection은 구체적으로 작은 window를 통해 보면서 주어진 point가 corner인지 아닌지 인식할 수 있다. 주어진 point에 window를 놓고 이를 수평 방향이나 수직 방향으로 이동시키면서 intensity의 변화가 큰 곳을 찾게 된다.
예를 들어 위에서 flat region에 point 하나가 있다고 해보자. 그리고 여기에 window를 놓고 여러 방향으로 shifting을 해본다. 이 경우에 어느 방향으로 shifting을 하든 window는 여전히 검은 pixel을 가지게 되어, 어느 방향으로도 변화를 인식할 수 없게 된다.

두번째 예시를 보도록 하자. 이번에는 point가 edge 위에 있다고 해보자. 그리고 다시 window를 놓고 여러 방향으로 shifting을 해볼 것이다. Window를 수직 방향으로 shifting하게 되면 intensity의 아무런 변화도 발견할 수 없다. 그러나 이를 수평 방향으로 shifting하게 되면 큰 변화를 발결하게 된다. 그래서 이 point를 edge라고 말할 수 있는 것이다.

마지막으로 이번에는 point가 corner에 있다고 해보자. 그리고 window를 놓고 여러 방향으로 shifting을 해보았을 때, 어느 방향으로 해도 intensity의 변화가 큰 것을 알 수 있다. 그래서 이러한 것을 통해서 이 point가 corner라고 말할 수 있게 된다.

Corner Detection: Mathematics

이를 기반으로 우리는 x축과 y축을 따라서 얼만큼 shifting했는지에 관해서 intensity의 변화를 계산하는 function을 이끌어낼 수 있다.

위의 식에서 $x_0,y_0$는 window의 중앙 좌표를 나타낸다. $u,v$는 얼만큼 이동했는지에 대한 shifting amount를 나타내고, $x,y$는 window pixel에 해당한다. 그러면 우리는 shifted pixel과 original pixel 사이의 difference를 더함으로써 shifted window와 original window 사이의 difference를 계산할 수 있다.

$\omega(x,y)$는 bow function이나 Gaussian function으로 정의되는 window function이다.
그러면 이제 다음 예시를 다시 보도록 하자.
위는 $E(u,v)$의 function 값을 서로 다른 $u,v$에 관하여 visualization한 것이다. $E(u,v)$ 각각의 center region은 $E(0,0)$에 대응된다. 먼저, 첫번째 경우 $E(u,v)$의 function 값이 모든 $u,v$에 대해서 0이 될 것이다. 왜냐하면 window가 shifting을 해도 intensity가 변하지 않았기 때문이다.

두번째 경우 $E(u,v)$의 function 값이 위와 같이 분포를 이룰 것이다. $u$의 변화는 큰 intensity 변화를 나타내지만, $v$의 변화는 어느 지점에서도 intensity 변화가 없다. 그래서 $E$의 function 값이 좌측과 우측 끝에서는 매우 크게 나타날 것이다.

마지막 경우 $E(u,v)$의 function 값이 중앙 쪽은 0이 되고, 외곽 쪽은 1이다. $u,v$의 값이 중앙으로부터 멀어지게 되면 이에 따라 $E(u,v)$의 값도 점점 커지게 된다.

Corner을 더 효율적으로 검출하기 위해서 Harris corner detector는 Taylor expansion을 사용해서 위의 식을 approximation하였다.

Approximated function은 $u,v$의 quadratic function으로, $2\times 2$ matrix M에 의해서 특징지어진다. 이 matrix는 second moment matrix로 image derivative $I_x, I_y$로부터 계산 되어진다.

Matrix $M$을 원래 식에 넣어서 계산하면 다음과 같다.

위 function에서 $(u^2I_x^2+2uvI_xI_y+v^2I_y^2)$ 부분은 $u,v$의 quadratic form이다. 그래서 만약 이 부분의 function 값들을 visualization하면 다음의 curved surface가 나오게 된다.
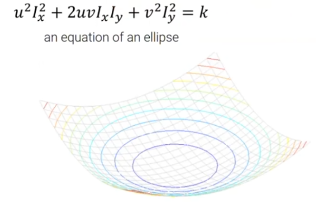이 surface의 모양을 보게 되면 $(x,y)$에 위치한 point들이 corner인지 아닌지 알 수 있다. Surface의 모양은 matrix $M$을 보면 알아낼 수 있다. 먼저, matrix $M$을 eigen value decomposition을 이용하여 다음과 같이 분해한다.

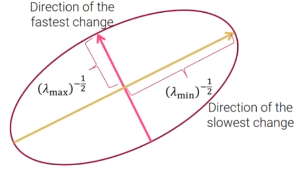
그래서 $\lambda_1,\lambda_2$는 matrix $M$의 eigen value이다. 여기서 만약 $\lambda_1$의 값이 크면, function 값이 각각 eigenvector에 대응되는 방향을 따라서 급격하게 바뀌는 것을 의미한다. 그래서 corner같은 경우 $\lambda_1,\lambda_2$ 모두 커야한다.

이를 기반으로 해서 corner response $R$을 다음과 같이 정의할 수 있다.

위의 식에서 $R$은 detreminant와 trace 사이의 difference로 정의된다. 이 식은 eigen value를 바로 사용하지 않고 determinant와 trace를 통해서 사용하게 된다. 왜냐하면 determinant와 trace를 계산하는 것이 eigen value를 계산하는 것 보다 더 쉽기 때문이다. 여기서 $\alpha$는 일반적으로 0,04부터 0,06까지로 작은 constant이다.
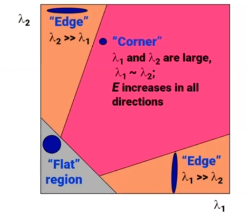Corner response $R$은 오직 $M$의 eigenvalue 값에만 의존한다. 만약 $M$이 크다는 것은 2개의 eigenvalue가 모두 크다는 것을 의미하고 이는 corner임을 나타낸다. 만약 $M$이 0에 가까우면 2개의 eigenvalue가 모두 0에 가깝다는 것을 의미하고 이는 flat region임을 나타낸다. 마지막으로 $M$이 0보다 많이 작으면 2개의 egienvalue 중 하나만 크다는 것을 의미하고, 이는 edge가 된다. 그래서 corner response를 통해서 corner을 검출할 수 있게 된다.

Harris Detector Algorithm

그래서 Harris corner detector algorithm은 다음과 같다.
먼저 모든 pixel에 대해서 image gradient를 계산하고, 각각의 pixel 주변의 window를 놓고 second moment matrix $M$을 계산한다. 그리고 각각의 pixel에 대해서 corner response function $R$을 계산하고, threshold $R$을 통해서 corner response $R$ 값이 큰 pixel을 찾는다. 마지막으로 response function 값으로부터 non-maximum suppression을 이용해서 local maxima를 찾는다. 결론적으로 local maxima가 검출 된 corner에 해당하게 된다.

Harris Detector: Some Properties

Harris corner detector는 몇가지 중요한 성질을 가지고 있다.

Rotation Invariance

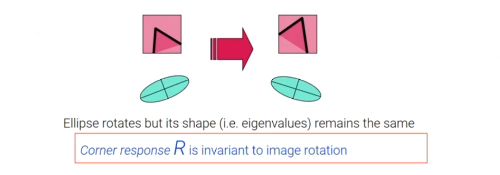첫번째는 rotation inavriance이다. 이것이 의미하는 것은 harris corner detector는 회전되어 있다고 하더라도 같은 corner을 검출할 수 있다. 이는 꽤 명백한 사실이다. 왜냐하면 corner는 비록 회전했다고 하더라도 여전히 corner이기 때문이다. Harris corner detector는 corner을 검출하기 위해서 설계되었다. Rotation invariance가 진정으로 의미하는 것은 corner response $R$이 비록 image가 회전했다 하더라도 변하지 않는다는 것이다.

그렇다면, 이 성질이 왜 중요한 것일까? 때때로 한 개체에 대해서 2개의 image를 가지게 된다. 카메라의 위치 때문에 한 image는 회전되어 보이게 된다. Rotation invariance는 만약 하나의 image로부터 corner가 검출이 되었다면, 이에 대응되는 다른 image의 corner 또한 image가 회전되었다고 하더라도 검출될 것이라는 것을 의미한다.

Partial Invariance to Affine Intensity Change

두번째 성질은 Harris corner detector는 affine intensity change에 대해서 부분적으로 invariant하다. Affine intensity change는 scaling과 intensity shift 혹은 translation의 조합을 의미한다.

Harris corner detector는 오직 image derivative를 이용해서 corner response 값을 계산한다. 그래서 corner response 값은 intensity shift에 invariant하다. 왜냐하면 이러한 shift는 derivative를 바꾸지 않기 때문이다.

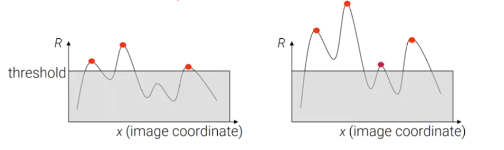반면, intensity scaling은 corner response 값을 바꾸게 된다. 이러한 변화 후에도 우리는 threshold를 corner response 값으로 사용할 수 있다. 만약 corner response 값이 여전히 큰 값으로 남아있다면, corner로 검출되어 질 수 있다. 그러나 몇몇 corner에서 response 값이 작아질 수 있어 scaling 후에는 놓치게 될 수 있다. 우측의 3번째 지점이 검출되어졌지만, scaling 후에 좌측을 보면 해당하는 지점이 더이상 feature point로 검출 되지 않았다.

그래서 결과적으로 Harris corner detector는 intensity scaling에 부분적으로 invariant하다. 이러한 intensity 변화에 대해서 이러한 invariance가 중요한 이유는 detector가 image 사이의 exposure difference 다룰 수 있다는 것을 의미하기 때문이다. 구체적으로 같은 개체가 다른 순간에 포착될 수 있다. 예를 들어서 건물의 사진을 낮에 찍는다고 했을 때 같은 빌딩을 밤에 다른 사진으로 찍을 수 있다. 그렇게 되면 image들은 완전히 다른 lighting conditon을 가지게 되고 같은 빌딩이 매우 다르게 나타난다. 그러나 detector가 intensity change에 invariant하다면 우리는 이렇나 exposure difference와는 상관 없이 여전히 같은 feature point를 얻을 수 있고, 이를 image alignment에 사용할 수 있다.

Non-Invariant to Image Sacle

지금까지 보았듯이 Harris corner detector는 image rotation에 invariant하고, intensity change에 있어서는 부분적으로 invariant하다. 그리고 이는 좋은 성질들이다. 그러나 Harris corner detector가 image scale에는 inavariant하지 못하다.
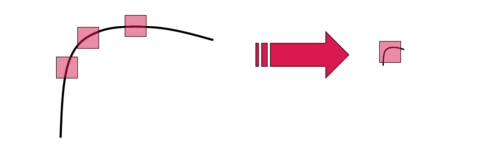예를 들어 같은 개체에 대해서 2개의 image를 얻었다고 해보자. 하나의 image는 우리가 그 개체에 매우 가까이 다가가서 얻은 것이다. 그래서 개체는 image 상에서 매우 크게 보일 것이다. 다른 image는 반대로 개체로부터 멀리 떨어져서 얻은 것이다. 그래서 image 상에서 개체는 매우 작게 보일 것이다.

그러면 image 상에서 같은 corner에 대해서 매우 다르게 보일 것이다. 같은 corner지만 scale은 매우 다를 것이다. 좌측 image에서 Harris corner detector는 모든 point들에 대해서 edge로 분류할 것이다. 그러나 우측 image에서 Harris corner detector는 같은 corner지만 corner라고 분류하게 될 것이다.

여기 보다시피 Harris corner detector는 image scaling에 대해서는 invariant 하지 못하다. 그래서 image alignment를 할 때 같은 개체지만 다른 크기의 image에 대해서 문제가 되곤 한다.

Scale Invariant Detection

그러면 어떻게 이 문제를 해결하고 scale invariance를 얻을 수 있을까? Image pyramid를 사용하면 해결할 수 있다. Image pyramid를 만들고 각각의 pyramid level에 대해서 corner를 검출하는 것이다.
예를 들어서 위의 point가 위의 scale에서는 edge로 검출될 것이다. Image pyramid를 사용하면 어느순간 특정 scale에 대해서 corner로 검출될 수 있다.
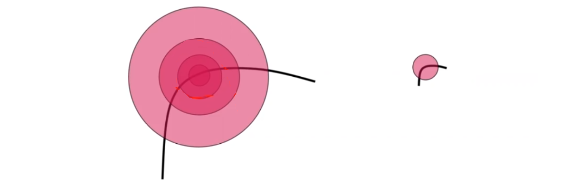그러면 각각의 corner에 대해서 검출하기 적절한 원과 scale이 존재할 것이다. 그렇다며 어떻게 적절한 원의 크기를 고를 수 있을까? 매우 간단하다. 각각의 corner에서 우리는 corner response 값에 따라 best corner의 scale을 선택할 수 있다.

Feature Selection

모든 pixel의 corner response 값을 계산한 후에는 이 값을 기반으로 몇개의 feature point를 선택해야 한다. 기본적으로 우리는 corner response 값이 큰 feature를 선택하고 싶다. 그러나 단순하게 corner resonse값을 thresholding한다면, 너무 많거나 혹은 너무 적은 feature point들이 선택되어 질 것이다. 게다가 선택된 feature point들이 골고루 분포하지 않을지도 모른다. 만약 어느 한 부분에 feature point들이 모여있다면 이후 진행되는 alignment step이 부정확할지도 모른다. 왜냐하면 image가 오직 일부분에 의해서 alignment되기 때문이다. 그래서 이 step에서 우리가 원하는 것은 적절한 수의 image 전반에 고르게 분포되어 있는 feature point를 얻는 것는다.
고르게 분포되어 있는 feature point들을 검출하기 위해서 adaptive non-maximal suppresion이라는 기법을 사용하게 된다. Adaptive non-maximal suppresion는 feature point 주변에 떨어져 있는 feature point를 식별하게 해주고, locally adpative한 방식으로 threshold를 선택하게 해준다. 그래서 우리는 image 전반에 고르게 분포되어 있는 feature point들을 검출할 수 있다.

Other Feature Detectors

지금까지 Harris corner detector에 대해서 알아보았다. 그러나 feature detector는 이외에도 SIFT, SURF, FAST, ORB 등 정말로 많다. Feature dectector가 달라짐에 따라 다른 특징들을 제공해주고 computational efficiency를 제공해준다. 예를 들어 SIFT나 SURF는 Harris corner detector와는 다르게 scale invariant하다. 또한, SURF와 같은 몇몇 feature detector는 특허에 의해 보호받고 있다. 그래서 학업적인 목적하에 SURF를 사용할 수 있고 상업적인 목적으로는 사용할 수 없다. 그래서 만약 feature detector를 사용하고 싶다면 각자의 특징들을 비교하고 적절한 것을 선택하면 된다. 많고 많은 detector 중에서 가장 많이 사용되는 것은 SIFT이다. SIFT는 특허에 의해 보호되고 있지만 학업적인 목적으로 사용이 가능하다. 그러나 올해 특허가 만료가 되어 자유롭게 사용할 수 있게 되었다. 대부분의 feature detector는 opencv에 내장되어 있어 찾아서 사용하면 된다.

Feature Matching

Feature point를 검출한 이후에 image alignment의 다음 step은 feature matching이다. 다음과 같이 2개의 image가 있다고 해보자.
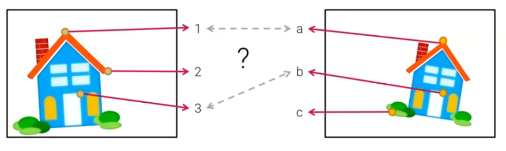그리고 image에는 검출된 feature point들이 존재한다. 그러면 이제 어떻게 검출된 feature point들을 matching할 수 있을까? 가장 간단한 아이디어는 같은 색의 feature point들을 matching하는 것이다. 위의 예시에서 3번과 b번은 같은 색을 가지고 있어 쉽게 matching이 가능하다. 그러나 나머지는 어느 것이 어떻게 matching되는지 쉽게 판단하기 어렵다.

그래서 새로운 방법으로 local image patch를 사용하게 되었다. 각각의 feature point는 image patch를 가지게 된다. 그러면 feature point들을 비교해서 2번보다 1번이 a와 잘 matching 된다고 판단할 수 있다. 그래서 우리는 local patch를 사용하는 것이 pixel의 color 값을 사용하는 것 보다더 robust하다고 말할 수 있다.

그러나 이는 충분히 robust할까? 만약 개체의 scale, orientation, brightness 등이 다른 경우에는 어떠할까? 이러한 경우에 local patch를 사용하더라도 feature point들을 robust하게 matching할 수 없다. 그래서 feature point들을 더 잘 설명할 수 있는 방법이 필요하다.

Feature Descriptors

우리가 정말로 원한는 것은 좋은 feature descriptor이다. Feature descriptor는 해당하는 point가 어떠한 feature을 가지는지 설명한다. 예를 들어, 우리는 pixel color나 local patch를 또한 feature descriptor로서 사용할 수 있다. 그러나 color나 local patch는 그 자체로 능력이 제한적이라서 이러한 문제를 다루기 위해서 더 좋은 feature descriptor를 사용해야 하고, 이를 위해서 2가지 조건이 필요하다.

첫번째로 "Good" feature descriptor는 반드시 rotation, scaling, brightness change 등과 같은 어떠한 transformation에도 invariant 해야한다.

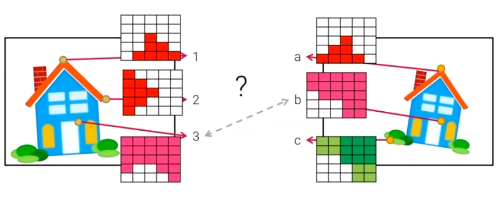
같은 집에 대해서 2개의 image가 존재한다. 이 image들에서 house는 카메라의 위치가 달라서 다른 orientation과 scale을 가지고 있다. 이러한 경우에도 good feature descriptor는 같은 설명을 해야하고, 그래서 feature point가 robust하게 matching 되어야 한다.

두번째는 반드시 distinctive 해야한다. 이는 서로 다른 feature라면 반드시 구분이 되어야 한다는 것을 의미한다. 만약 1번과 2번이 다른 feature라고 설명하지 못하면 어느 것이 a와 matching 되는지 설명할 수 없다.

Descriptors Invariant to Roation

그러면 어떻게 이러한 조건들을 만족할 수 있을까? 예를 들어 image rotation과는 상관없이 local image patch를 수정해서 feature descriptor를 이끌어낼 수 있다.

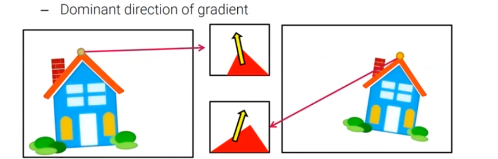
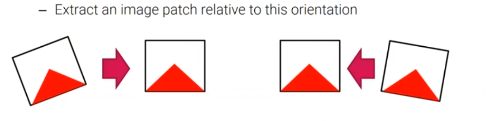각각의 feature point로부터 local image patch를 추출할 수 있고, 각각의 patch에 대해서 image gradient로부터 지배적인 방향을 계산할 수 있다. 그러면 이 방향을 기반으로 우리는 image patch를 회전시킬 수 있고, image rotation의 차이를 제거할 수 있다. 결과적으로 회전이 된 patch들은 image rotation에 invariant하고, 우리는 image rotation에 invvariant한 feature descripotr를 얻을 수 있다.

Feature descriptor도 또한 널리 연구가 되어져왔다. 그래서 많은 feature descriptor를 사용할 수 있다. SIFT와 SURF와 같은 몇몇 feature detector들은 자신만의 descriptor를 가지고 있다. 그리고 다른 경우에는 오직 descriptor들이 제공되어지기 때문에 detector와 따로 사용하면 된다.

만약 라이선스에 문제가 없다면 SIFT나 SURF를 이용하는 것이 좋다. 학업적인 목적으로 가장 많이 사용되기 때문이다. SIFT는 특허가 만료되었기에 자유롭게 사용하면 되지만, SURF는 여전히 보호되고 있어서 오로지 학업적인 목적으로만 사용해야 된다. 만약 opencv를 사용하고 라이선스로부터 자유로운 detector와 descriptor를 사용하고 싶다면 SIFT나 ORB를 사용하는 것이 좋다. 마지막으로 만약 빠른 속도의 수행능력을 보여야하는 것이 아니라면 굳이 detector와 descriptor를 비교하는데 너무 많은 시간을 사용하지 않아도 된다.

Feature Matching(con't)

검출된 feature들에 대해서 descriptor를 얻었다면 마침내 image를 align 할 준비가 되었다.
위의 image에서 빨간 점들은 검출된 feature point들이다. 그리고 아래의 patch는 feature descripor이다. Image alignment에서 우리는 각각의 image로부터 아마 수백개의 feature point들을 가지게 될 것이다. 그래서 어떻게 이 point들을 matching시킬까?

Feature matching을 위해서 우리는 exhaustive matching을 사용한다. Exhaustive matching에서 하나의 image에 있는 각각의 feature에 대해서 우리는 다른 image에서 모든 feature들을 봐야한다. 그래서 이는 computationally heavy method이다. 그래서 hasing이나 kd=tree처럼 가장 근접한 이웃에 근사하는 방법과 같이 속도가 빠른 방법들도 존재한다. 여기서 이 내용들을 다루지는 않을 것이고, 기존의 방법들을 많이 사용하니까 잘 알아두면 좋다. 비록 수백개의 feature point들이 있다고 하더라도 그렇게 많은 양은 아니라서 exhuastive matching 방법이 크게 느리지는 않다. 그러니 자유롭게 사용해도 상관없다.

Feature matching이후에는 위와 같이 match들을 가지게 된다. 위의 선들은 macthing이 된 feature point들을 가리킨다. 그러나 종종 부정확하게 matching이 된 point들도 존재한다. 이 match들로부터 transformation을 예상할 수 있을까? 잘못 matching이 된 point들인 outlier들 때문에 그렇지 않다. 만약 outlier가 존재하지 않으면 단순히 least square problem을 풀어서 transformation을 찾으면 된다. 그러나 outlier는 상당한 error를 만들어내어 정확한 transformation을 구할 수 없다.

Outlier Rejection

그래서 robust하게 transformation을 구하기 위해서는 이러한 outlier들을 다룰 줄 알아야 한다. 즉, transformation을 구하는데 outlier를 제외시켜야 한다. 어떻게 할 수 있을까? RANdom SAmple Consensus(RANSAC)이라는 방법을 통해서 가능하다. RANSAC은 가장 많이 사용되는 outlier rejection method 중 하나고, computer vision에서 정말 중요한 부분이라서 어떻게 동작하는지 알아두는 것이 중요하다.

RANSAC

지금부터 RANSAC이 어떻게 동작하는지 보도록 하자.
먼저 우리는 2개의 image를 가장 잘 연결해주는 translation을 찾기를 원한다고 하자. 2개의 image가 있고 match들이 화살표로 표시가 되어있다. 대부분 괜찮지만 2개 정도가 정확하지 않다.
이 match들 중에서 RANSAC algorithm은 무작위로 하나의 match를 고르고 선택된 match로부터 translation vector를 계산한다.
그러면 algorithm은 계산된 translation vector와 일치하는 inlier의 개수를 센다. 이 경우에는 5개의 inlier가 존재하고 2개의 outlier가 생기게 된다. 만약 우리가 찾은 translation vector 좋은 경우에는 최대한 많은 match들이 존재한다는 것을 설명하는 것이 가능하다. 만약 translation vector가 좋지 않은 경우에는 적은 양의 match들만을 설명하게 된다. 이 경우에는 5개의 match를 설명하기 때문에 좋은 경우에 해당한다.

Algorithm은 이러한 과정을 모든 inlier에 대해서 반복하고 가장 많은 inlier들을 set으로 묶어서 가지게 된다. N번의 반복이 끝난 후에는 가장 많은 inlier가 포함된 set을 가지고 있을 것이다. 그러면 set으로부터 algorithm이 translation vector의 평균을 계산하게 된다. 최종적으로 가장 큰 set을 설명하는 하나의 vector가 생기게 된다. 이렇게 나온 translation vector는 하나뿐이고 우리가 찾고 싶어했던 결과가 된다.

RANSAC for Estimating Homogrphy

다음은 homography를 구하는 RANSAC의 pseudocode이다.
우리는 전체 과정을 N번 반복하고, 각각의 반복 과정에는 무작위로 4개의 feature point 쌍을 고르게 된다. 왜냐하면 homogrpahy를 구하기 위해서는 4개의 correspondoence를 필요로하기 때문이다. 4개의 쌍에 대해서 homography를 계산하고 inlier의 개수를 셀 수 있다. 총 N번의 반복 후에는 inlier가 가장 많이 포함된 set을 가지게 되고, 이 set으로부터 least-square problem을 풀어서 최적의 homography $H$를 계산할 수 있다.

Example

Feature Detection

각각의 image로부터 feature point들을 검출할 수 있다.

Feature Matching & Homography Estimation Usign RANSAC

그러면 feature matching을 진행하고 RANSAC을 이용해서 homography estimation을 할 수 있다.

Align Two Images Using Estimated Homography

Homography를 구하면 하나의 image를 homography를 이용해서 warping하고 붙일 수 있다. 그러면 최종적으로 panorama image를 얻을 수 있다. 이 경우에는 단순히 다른 하나를 이어 붙인 것이기에 이미지 사이의 seam이 존재하게 된다. Blending method를 이요해서 seam을 제거할 수 있다.

Direct vs. Feature-Based

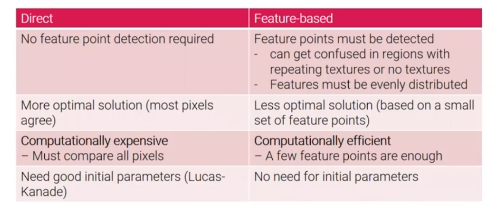2개의 방법 모두 각자 장단점이 존재한다. Direct alignment는 feature point detection을 하지 않는다. 반면, feature-based alignment는 필요로 한다. 그렇기 때문에 feature-based alignment는 단점이 어느정도 존재한다. Feature-base alignment는 반복되는 texture 또는 texture의 부재로로 인해 region이 혼동될 수 있습니다. 예를 들어 겉보기에 똑같은 창문이 많은 건물이 있다고 하면, feature matching이 매우 어려울 수 있다. 또한 feature는 고르게 분포되어있지 않으면 정확하게 alignment를 하기 어렵다. 그러나 하늘과 같은 region은 검출되는 특징이 크게 없기 때문에 이러한 region을 alignment하는 것은 다소 어렵다.

두번째로 direct alignment는 최적의 해가 많이 존재한다. 왜냐하면 대부분의 pixel들이 일치하는 transformation을 찾기 때문이다. 반면 feature-based alginment는 최적의 해가 적다. 왜냐하면 적은 양의 feature point set을 사용하기 때문이다.

세번째로 direct alignment는 모든 pixel들을 비교해야해서 computationally expensive하다. 반면, feature-based alignment는 적은 양의 feature point들이면 충분하기 때문에 computationally efficient하다.

마지막으로 direct aligntment는 Lucas-Kanade method와 같이 좋은 initial parameter들이 필요하다. 그러나 이는 얻기 어렵다. 반면에 feature-based alignment는 initial parameter를 필요로 하지 않는다.

두 방법 모두 장단점이 존재하지만, feature-based alignment가 더 많은 옵션이 있다. Direct alignment는 매우 정확한 alignment인 경우에 주로 사용된다.