[계산사진학] Morphological Image Processing

Morphology

Morphology라는 단어는 일반적으로 동물과 식물의 형태와 구조를 다루는 생물학의 한 분야를 가리킨다. 그러나 이 단어가 image processing에서는 수학적으로 사용이 된다. Morphology는 boundary, skeleton, convex hull과 같은 영역 형상의 표현과 설명에 유용한 image component를 추출하는 도구이다. Morphology 기법은 또한 image의 전처리나 후처리에도 사용이 된다.

Morphology 혹은 morphological image filtering은 binary image를 다룰 때 특별히 유용하게 사용된다. 예를 들어서 optical charater recognition(OCR)을 한다고 해보자. 다음은 스캔한 문서를 예시로 보여주는 것이다.
이러한 문서를 보고 바로 문자를 인식하는 것은 주변의 noise로 인하여 다소 어렵다. 그래서 Otsu's method와 같은 binarization method를 이용해서 이 문서를 noise가 없는 binarized image로 바꿀 수 있다. 결과를 보면 주변에 noise는 사라졌지만, 오히려 글자 자체에 noise가 생기는 것을 볼 수 있다. 이러한 경우에 morphological filtering을 이용해서 글자 모양을 수정할 수 있다. 글자에 생긴 구멍을 morphology를 이용하면 구멍을 채울 수가 있어서 더 선명한 글자를 읽을 수 있다.

이제 image의 관점에서 morphology가 무엇인지 자세하게 볼 것이다. Morphology는 기본적으로 set theory를 기반으로 한다. 수학적으로 정의 된 morphology에서 set은 image에 있는 개체들을 나타낸다. Binary image에서 set의 element들은 개체에 속하는 pixel들의 $(x,y)$ 좌표를 의미한다. Gray-scale image의 경우에는 set의 element들은 $(x,y,z)$ pixel 좌표와 그 intensity를 의미한다. 다음 binary image를 보도록 하자.
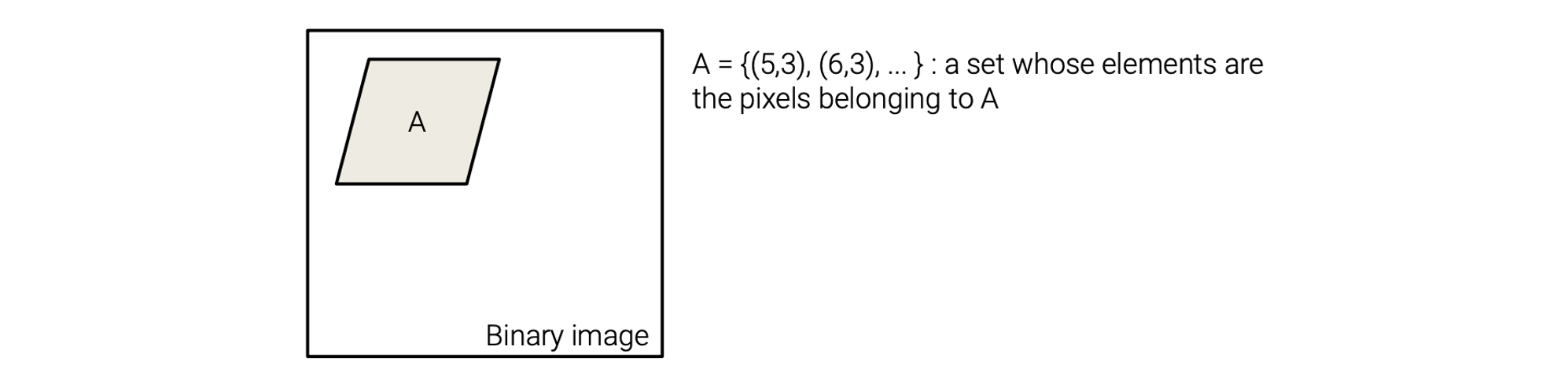우리는 이 예시를 보고 $A$에 해당하는 pixel들 이용해서 $A$라는 set을 정의할 수 있다.

Basic Set Theory

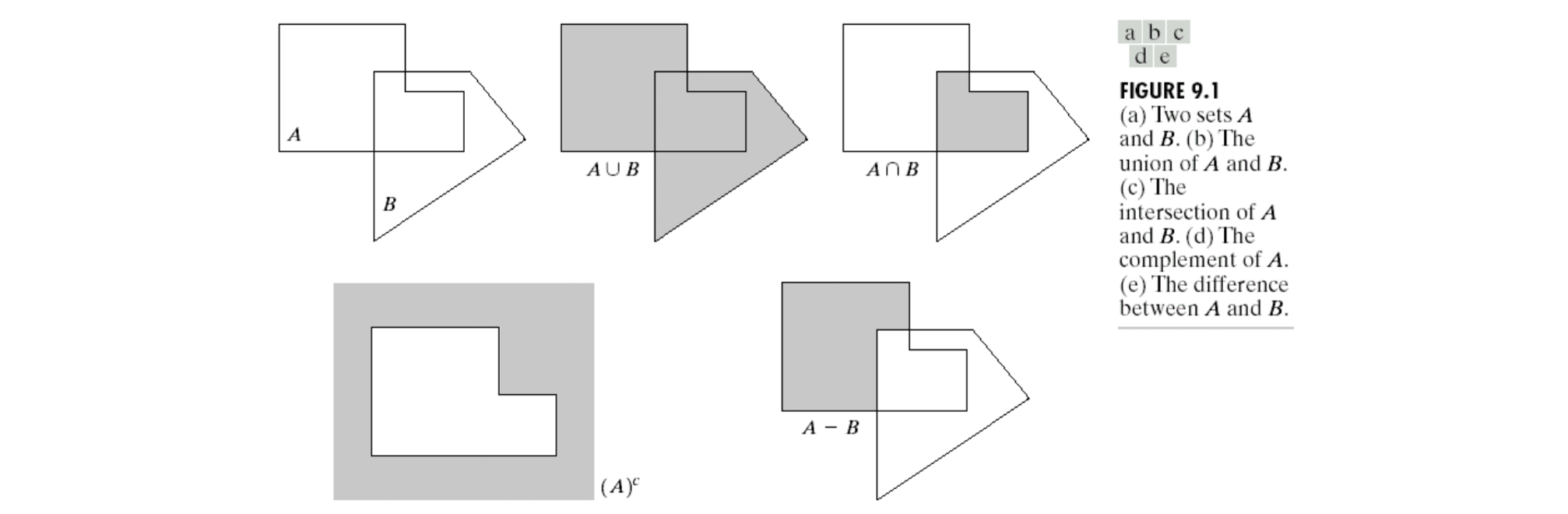
또한 개체를 set으로 정의하고나면 binary image에서 개체들로부터 set operation들을 정의할 수 있다. A와 B라는 개체를 정의하고 union, intersection 등 set operation을 다음과 같이 정의할 수 있다.

Reflection and Translation

추가로 2개의 operation인 reflection과 translation을 정의할 수 있다. Set $B$의 reflection은 다음과 같이 정의가 된다.

이 정의로부터 $B$의 각각의 element $b$ 에 대해서 minus 부호를 부여해서 새로운 set $\hat{B}$를 얻을 수 있다. 다음은 set $A$의 translation이다.

$z=(z_1,z_2)$라는 점에 대한 set A의 traslation을 보면, 각각의 element $a$ 에 대해서 $z$ 를 더해서 translation set을 얻을 수 있다.

Logic Operations

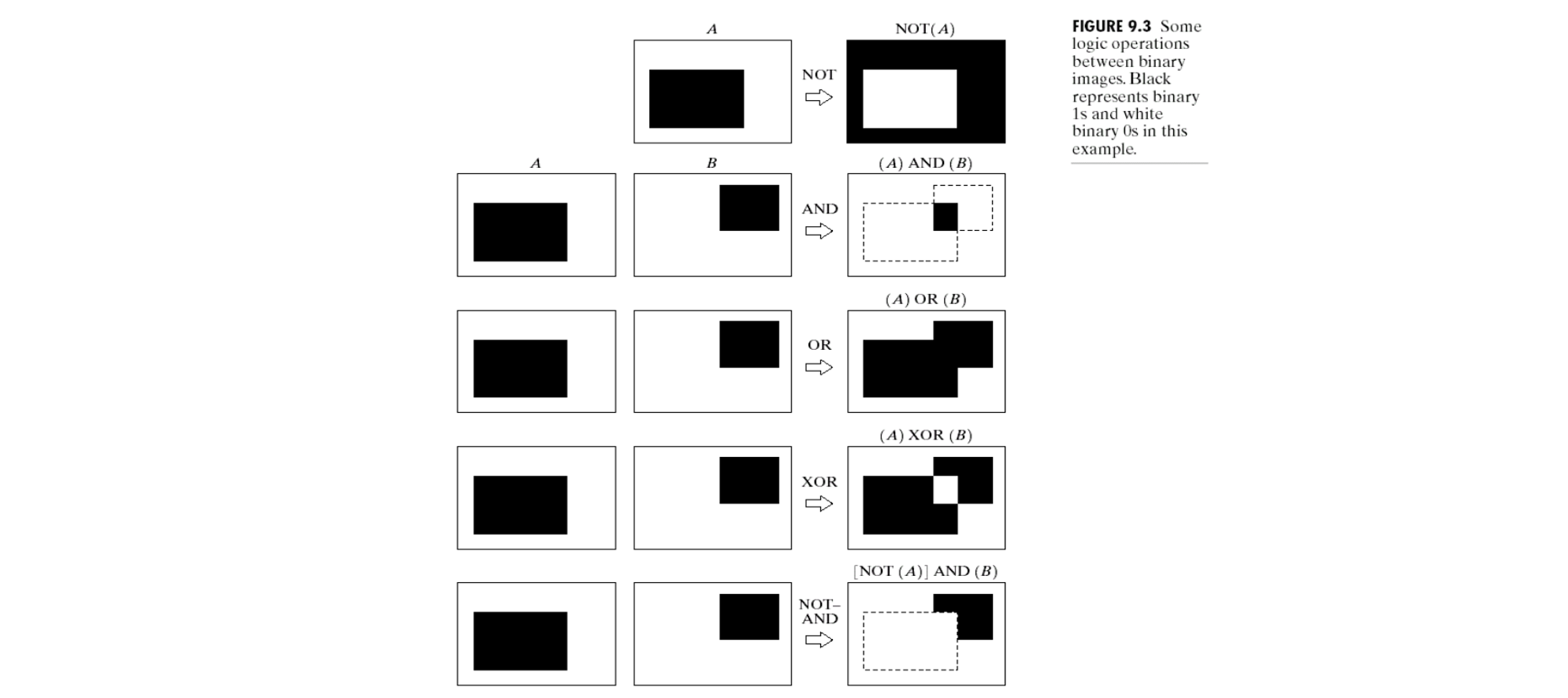
또한 logic operation을 이용해서 morphological operation을 설명할 수 있다. 다음은 기본적인 logic operation을 정리한 것이다.
AND operatior는 둘 다 1인 경우에 1이 된다. OR operator는 둘 중 하나라도 1인 경우에 1이 된다. NOT operatior는 하나에 대해서 0인 경우에 1이 되고, 1인 경우에 0이 된다.

Logic Operations Involving Binary Images

이러한 logic operator들은 binary image를 다루는데 사용된다. 2개의 binary image A와 B가 있다고 해보자. 그리고 image 상에서 검정색은 1을 나타내고, 하얀색은 0을 나타낼 때 다음과 같이 operator를 이용해서 새로운 binary image를 얻을 수 있다.

Morphological Operations on Binary Images

이러한 내용들을 생각하면서 가장 먼저 볼 내용은 binary image에 대한 morphological operation이다.

Dialation and Erosion

Morphology에는 2개의 근본이 되는 operator로 dilation과 erosion이 있다. 이 2개의 operator가 근본이 되는 이유는 다른 morphological operation들이 이 2개를 기반으로해서 만들어졌기 때문이다. 이 operator는 서로 반대로 동작한다. Dilation이 image를 확장시킨다면, erosion은 이미지를 줄어들게 한다.

Dilation

2개의 binary image $A$와 $B$가 있다고 해보자. 이 image들은 set으로 생각 할 것이다. 그러면 이제 B에 의한 A의 dilation을 다음과 같이 정의할 수 있다.

$\hat{B}$는 $B$의 reflection을 나타내고, 아래 첨자 $z$는 translation을 의미한다. 그래서 $(\hat{B})_z$ 는 각각의 $z$에 대해서 먼저 z에 의한 B의 reflection의 translation을 계산한다는 것이다. 그리고 이 결과와 $A$의 교집합이 공집합이 아니라면 그 결과가 $z$ 자체로 element가 된다.

우리는 여기서 $B$를 structring element라고 부를 것이다. 그리고 이러한 operation은 일종의 convolution의 binary version이다. 그래서 dilation은 convolution과 비슷하게 동작하게 된다. Convolution operation에서 structuring element 역시 flip 되기 때문에 위와 같은 정의를 사용하게 된 것이다. 여기서 flipped라는 것의 의미는 $B$의 reflection을 사용했다는 것을 나타낸다. Dilation operation이 convolution operation과 비슷하다고 했기 때문에 dilation은 convolution과 thresholding에 의해서 동작이 된다. 예를 들어서 $B$를 이용해서 image $A$를 convolution kernel로서 convolve 할 수 있고($A = \text{conv2}(A,B)$), 후에 $A$ 결과로부터 0이 아닌 pixel들을 1로 설정할 수 있다($A[A>0]=1$). 이렇게하면 dialation operation과 같이 정확히 똑같은 결과를 얻을 수 있다. 다음은 dilation operation의 예시이다.

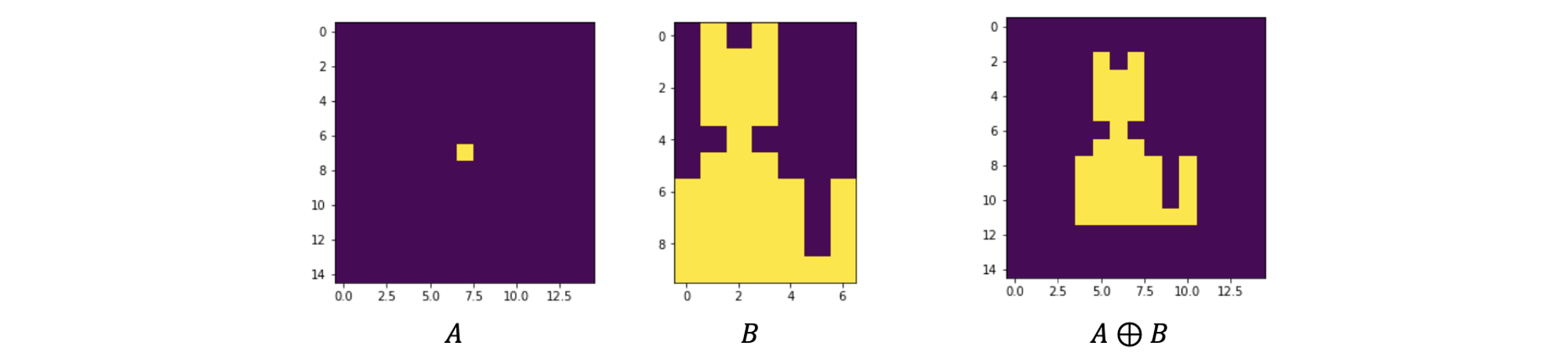위와 같이 $A$라는 image가 있고 가운데 노란 점은 1, 밖에 보라색 점들은 0을 나타낸다. Structuring element로서 binary image $B$를 사용해서 우측과 같이 dilation 결과를 얻을 수 있다.

Dilation이 동작하는 방법은 source image에서 current pixel로 target pixel이 있을 때, 만약 이 pixel이 1이라면 structring element를 이 pixel 위에 올려놓고, 1이 아니라 0이라면 그냥 이 pixel은 넘어가면 된다. 이렇게 모든 pixel들을 검사하면서 pixel이 0이 아니라면 여기에 structuring element를 놓고 결과를 내면 된다. 그리고 만약 다른 pixel도 0이 아니거나 1이라면 계속해서 structring element를 놓고 겹쳐서 결과를 내면 된다. 이러한 식으로 dilation이 동작하게 된다. 이러한 과정은 convolution operation과 매우 유사하다. 다음은 또 다른 dilation의 예시이다.

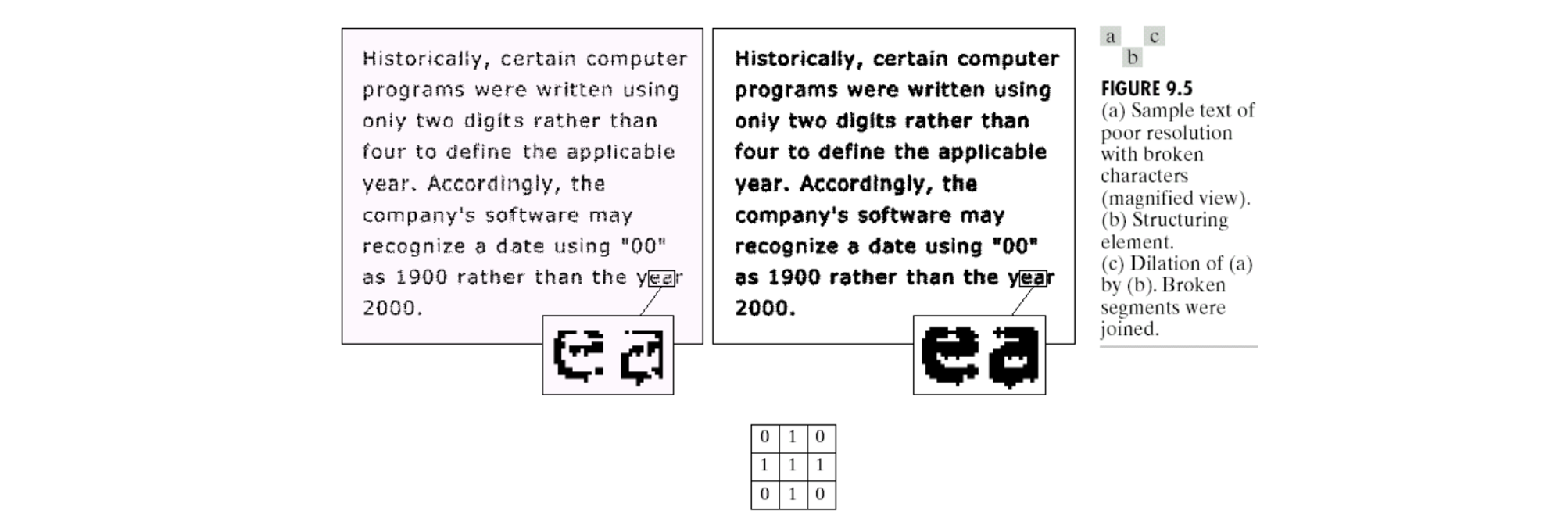다시 문자를 스캔한 binary image를 보면 검정색은 1을 나타내고, 하얀색은 0을 나타낸다. 자세히보면 좌측의 image는 noise가 심해서 구조적으로 부족하거나 구멍들이 존재한다. 이를 해결하기 위해서 위와 같이 binary image를 structuring element로 사용해서 dilation operation을 수행하려고 한다. 그러면 그 결과 우측과 같이 채워진 글자들을 볼 수 있다.

Erosion

두번째 근본이 되는 operation으로 erosion을 볼 것이다. Set $A, B$에 대해서 $B$에 의한 $A$의 erosion은 다음과 같이 정의가 된다.

이렇게 수학적으로 정의하면 다소 어려울 수 있으니 다음의 예시를 통해서 이해해보려고 해보자.
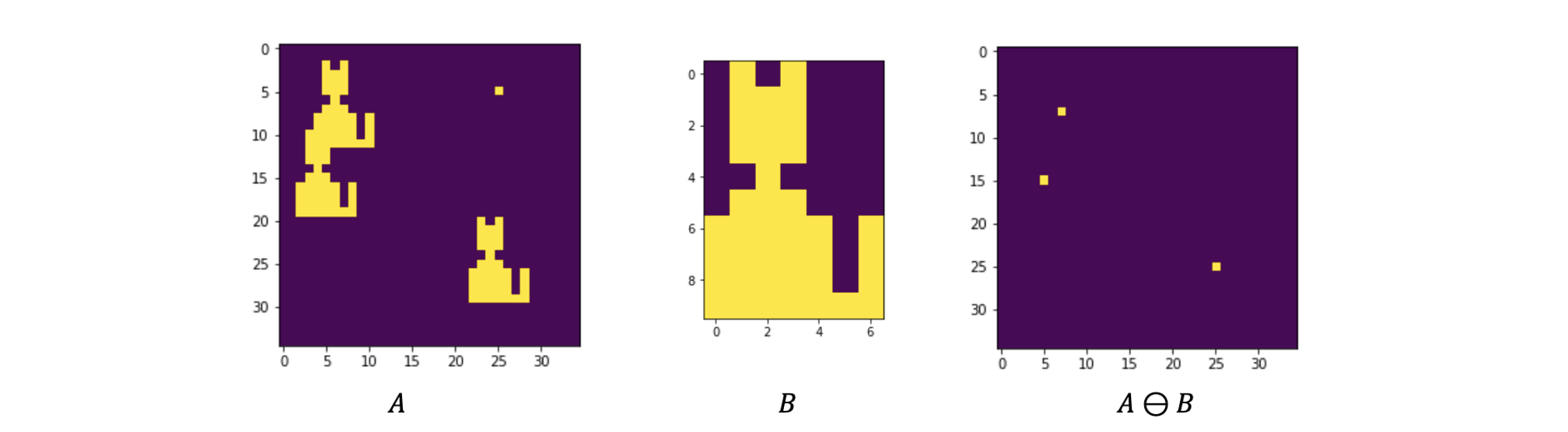Binary image $A, B$가 있고, $B$를 structuring element로 사용하려고 한다. Erosion operation에서는 $A$의 지역적인 부분과 structuring element와 비교를 한다. 그래서 만약 $B$가 $A$에 있다면, 이를 반영해서 우측의 결과를 만들게 된다.

구체적으로 이야기하면 $A$의 모든 target pixel마다 어느정도 크기의 window를 설정하고 이 local window와 structuring element를 비교해서 structuring element가 해당하는 window에 포함이 되어있는지 아닌지를 판단한다. Local window 내에서 모든 pixel이 structuring element의 1과 대응된다면, 이러한 경우에 결과에다가 값을 1로 설정하면 된다. 위의 예시에서 1인 지점이 3군데가 존재하는 이유는 $A$에 3개의 local window가 structuring element를 완전히 포함하기 때문이다. 그래서 우리는 erosion operation은 source image 내의 structuring element와 대응되는 하얀 개체를 줄어들게 한다고 말할 수 있다.

Dilation과 erosion operation은 서로 duals라고 할 수 있으며, 이는 다음과 같지만 크게 중요하지 않다.

그래서 erosion의 예시를 좀 더 보도록 할 것이다.
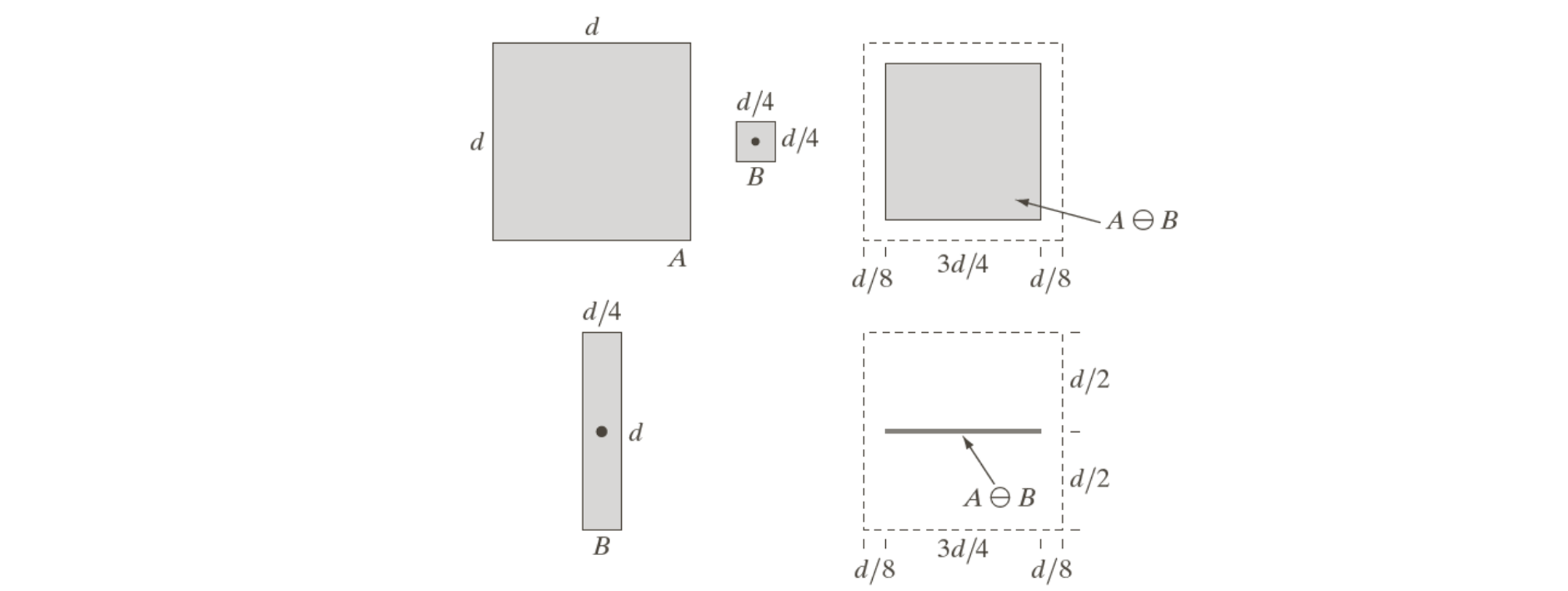Structuring element $B$의 모양에 따라 그 결과가 달라지는 것을 볼 수 있다.
Erosion operation은 binary image로부터 관련이 없는 디테일한 부분을 지우는데 사용된다. 좌측의 image를 source image로 하여 특정 크기보다 큰 사각형만을 찾고 싶다고 해보자. 그러면 structuring element를 가장 큰 사각형의 크기와 같게 해서 erosion operation을 취하면 structuring element보다 크기가 작은 사각형은 전부 사라지고 중앙의 image와 같이 3군데만 결과가 남을 것이다. 그리고 중앙의 image를 같은 structuring element를 이용해서 dilation operation을 취하면 우측의 image와 같이 될 것이다.

Opening

이렇게 dilation과 erosion을 조합하여 다른 morphological operation을 만들 수가 있다. 첫번째가 바로 opening operation이다. Opening operation은 일반적으로 개체의 윤곽선을 부드럽게 하고, 좁은 지협을 파고, 가느다란 돌기를 제거할 때 사용한다. Structuring element $B$에 의한 set $A$의 opening operation은 다음과 같이 정의된다.

이 정의를 보면 먼저 erosion을 수행하고 dilation을 수행하게 된다.
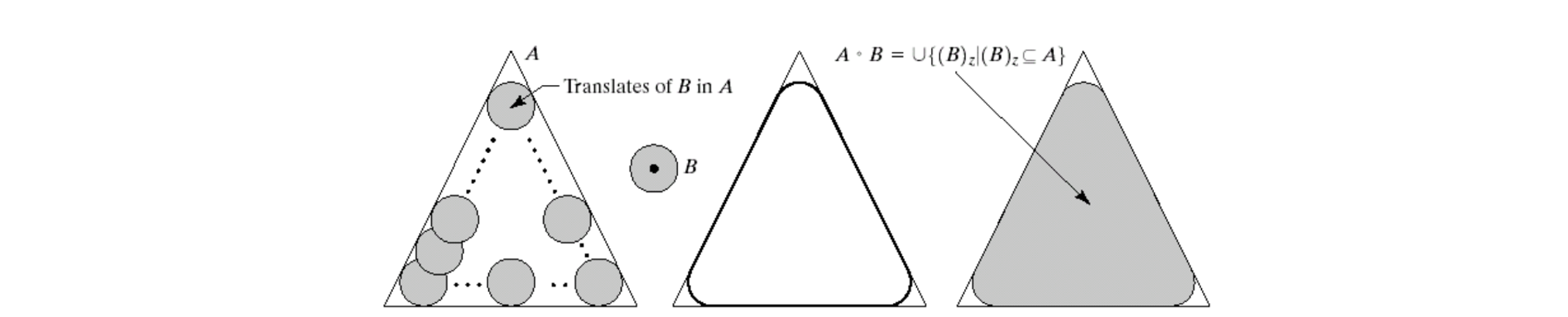이 예시에서 삼각형을 source image $A$로, 작은 원을 structuring element $B$로 사용할 것이다. 먼저 erosion을 하면 중앙의 끝이 부드러운 작은 삼각형을 얻게 되고, 다시 dilation을 하면 속이 채워진 부드러운 삼각형이 만들어진다. 이러한 과정이 바로 opening이 된다.

Closing

두번째는 closing operation이다. Structuring element $B$에 의한 set $A$의 closing operation은 다음과 같이 정의된다.

이 정의를 보면 먼저 dilation을 수행하고 erosion을 수행하게 된다.

Opening and Closing

다음은 opening과 closing의 차이를 보여주는 예시이다.
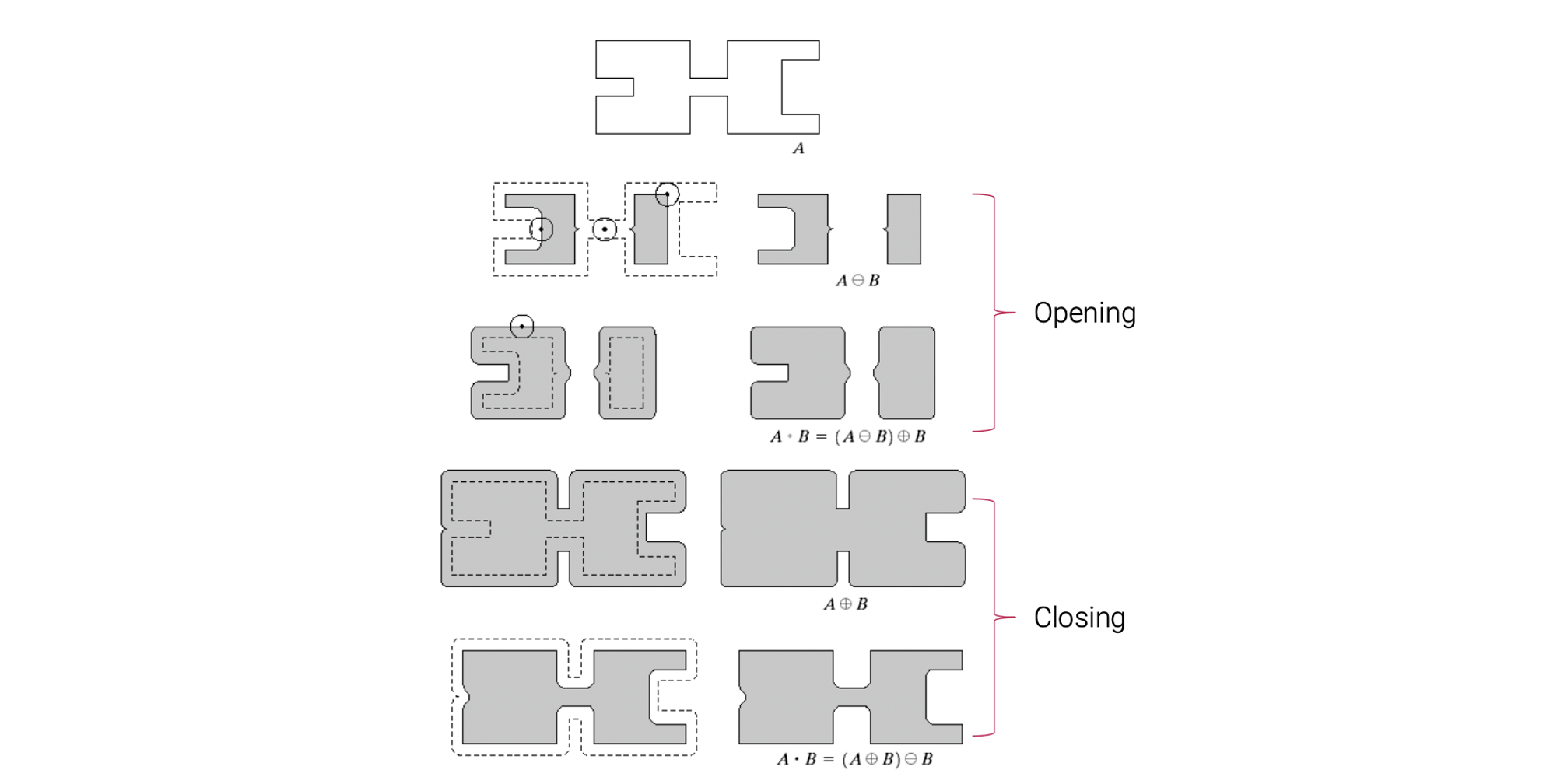작은 원을 source image로 사용할 때, opening operation은 먼저 erosion을 하고 dilation을 한다. Structuring element보다 image의 부분적인 구조가 더 작다면 지워지고 다시 dilation을 통해서 원래 크기로 채울 수가 있다. 그 결과 끝은 부드러우면서 structuring element보다 작은 부분은 지워지게 되었다.

다음으로 closing operation은 먼저 dilation을 하고 erosion을 한다. 그래서 결과적으로 dilation을 통해서 structuring element보다 작은 구멍을 채우는 대신 커진 크기는 원래 크기로 돌리기 위해서 erosion을 진행하게 된다. 그 결과 structuring element보다 작은 부분을 채우게 되었다.

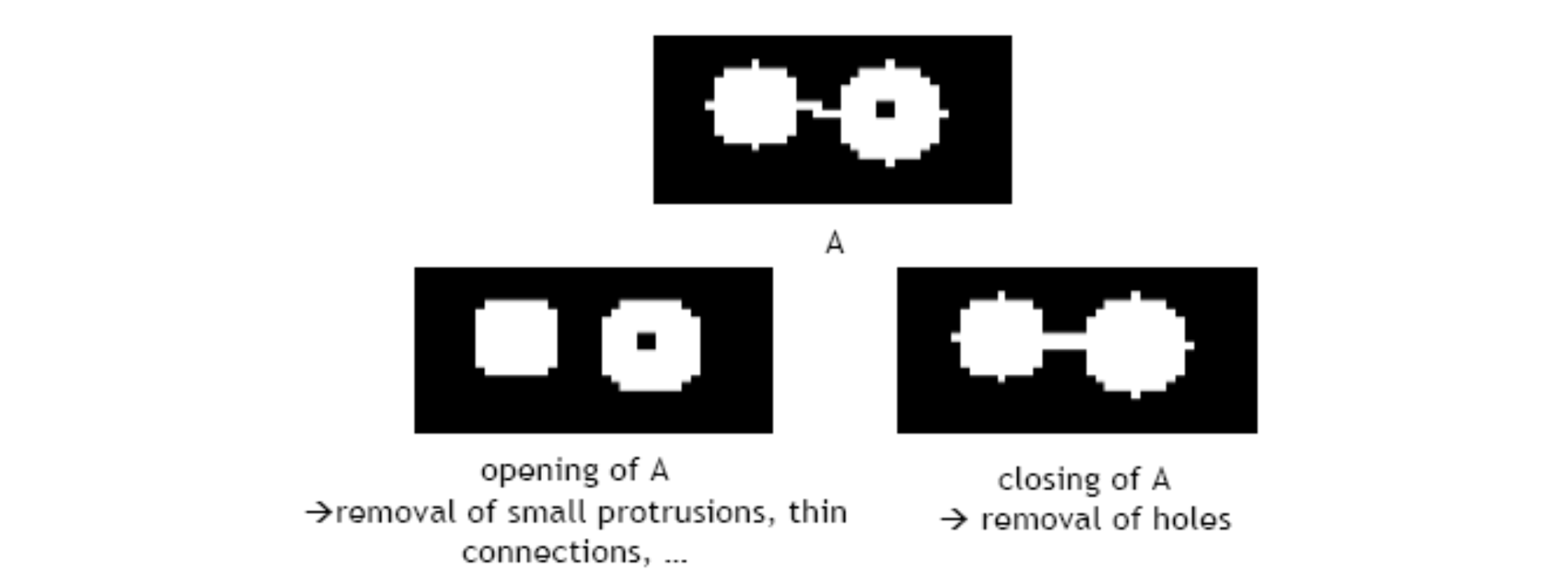위의 예시에서 source image $A$를 보면 하얀 원 안에 작은 검은 사각형이 있고, 하얀 원끼리 잇는 얇은 선이 있다. Opening operation을 통해서는 하얀 얇은 부분을 지울 수 있고, closing operation을 통해서는 작은 검은 사각형을 지울 수 있다.

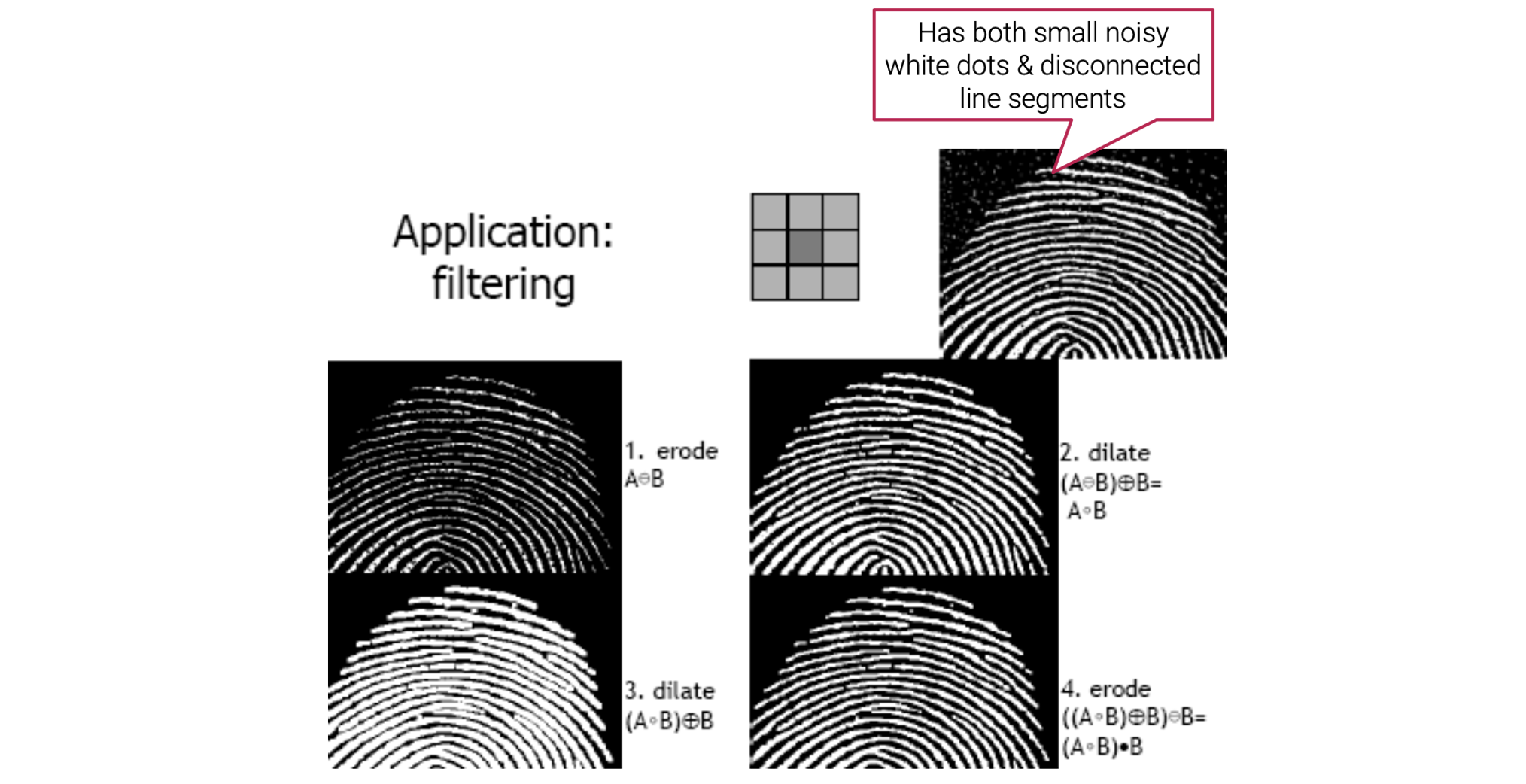이 예시는 좀 더 실용적인 예시로 지문을 binary image로 나타낸 것이다. 지문이 끊어지거나 noise가 많은데, 이를 해결하기 위해서 먼저 erosion을 통해서 하얀 noise를 지웠다. 그리고 이를 키우기 위해서 dilation을 이용했다. 이렇게 opening operation 과정을 한 것이 1, 2번이다. 하지만 끊어진 문제는 해결이 되지 않아 다시 dilation을 하고 크기를 돌리기 위해서 erosion을 이용했다. 그 결과가 4번이고 이렇게 3, 4번 과정이 closing operation에 해당한다.

Hit-or-miss transformation, boundary extraction, region filling, extraction of connected components, convex Hull, thinning, thickening, skeletons, pruning 등은 지금까지 살펴 본 operation을 이용하는 여러 예시들이다.

Gray-Scale Morphology

지금까지 binary image에서의 morphology에 대해서 알아보았다. 그러나 gray-scale image에서도 morphology를 적용할 수가 있다. 그래서 지금부터는 gray-scal morphology와 관련하여 기본적인 개념에 대해서 알아볼 것이다. Gray-scale morphology는 그렇게 널리 사용되지 않기 때문에 간단하게 볼 것이다.

Gray-scale morphology에서는 gray-scale image를 다루게 된다. 그러나 여기서도 binary structuring element를 사용하거나 아니면 gray-scale structuring element를 사용하게 된다. Structuring element를 어느 것을 사용하느냐에 따라서 두 종류의 morphological operation을 사용하게 된다. 만약 structuring element가 binary image라면 우리는 이를 flat structuring element라고 부른다. 그렇지 않고 structuring element를 gray-scale image를 사용한다면, 이를 nonflat structuring element라고 부르게 된다. 이번에는 gray-scale morphology에서 flat structuring element를 사용하는 경우만 다룰 것이다.

Grayscale Erosion and Dilation

Flat

먼저 flat structuring element를 사용하는 grayscale 버전의 dilation과 erosion을 보도록 할 것이다. Erosion과 dilation operation은 다음과 같이 정의될 수 있다.
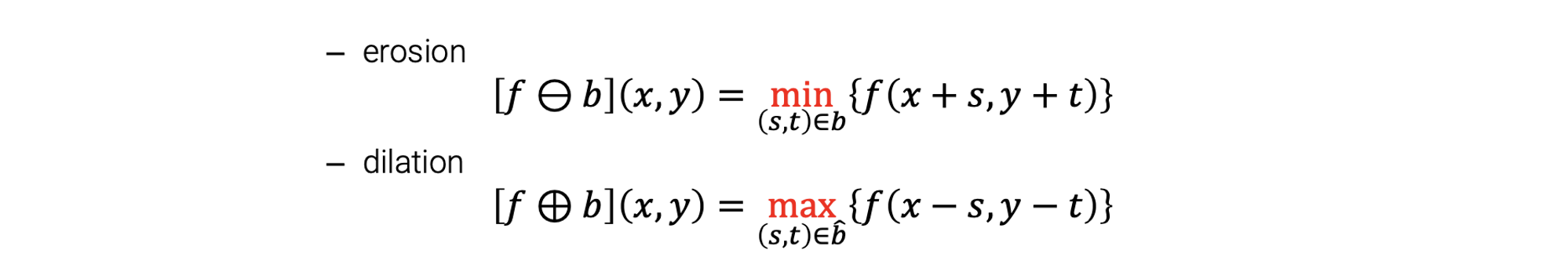이러한 정의도 binary image에 사용이 되곤 했다. 그래서 이러한 정의는 위에서 보았던 정의와 마찬가지로 똑같은 결과를 만들어낸다. 이는 일종의 binary의 경우의 확장판이라 생각해도 좋다.
Erosion은 밝은 부분을 줄이는데, 이는 binary image의 erosion과 비슷하다. 또한 dilation은 밝은 부분을 키우는데, 이는 binary image의 dilation과 비슷하다.

Nonflat

다음은 nonflat structuring element를 사용하는 grayscale 버전의 dilation과 erosion이다.

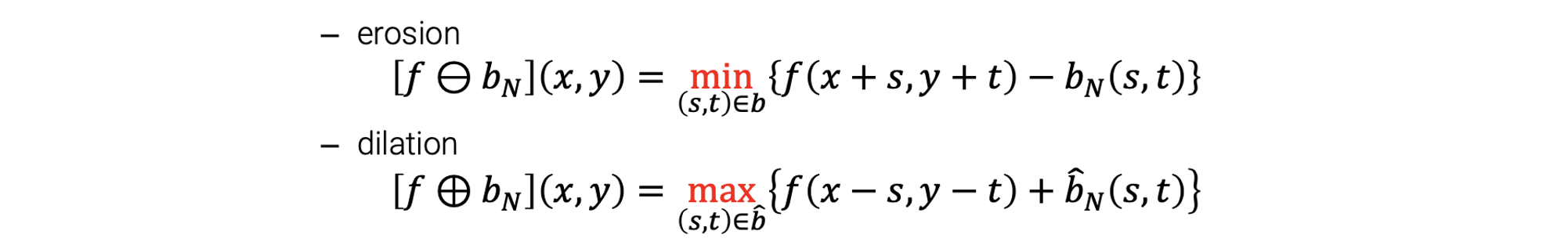
Grayscale Opening and Closing

Grayscale opening과 closing은 binary opening과 closing처럼 정의할 수 있다.

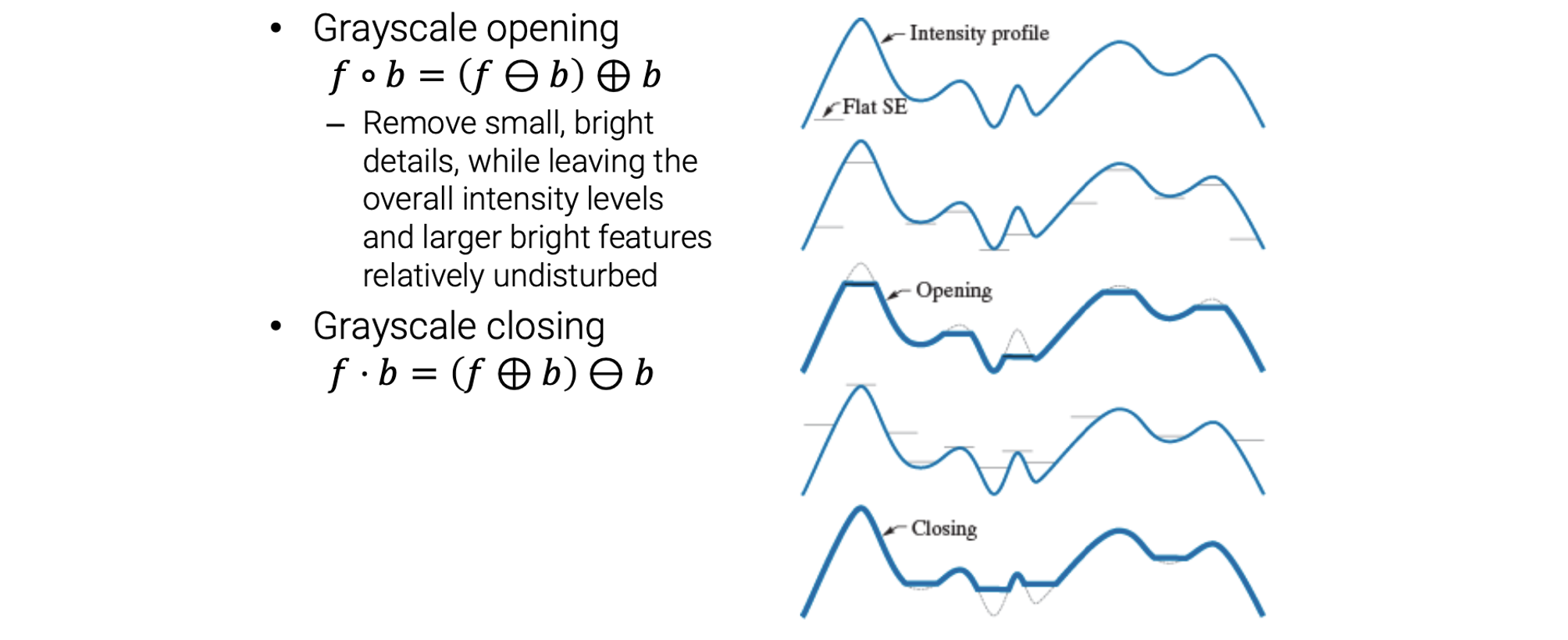
Grayscale opening은 binary opening operation과 비슷하게 작은 하얀 부분을 지우고, 또한 grayscale closing은 binary closing operation과 비슷하게 작은 검정 부분을 지우게 된다.

Morphological Smoothing

다음은 grayscale morphology의 예시로, Cygnus loop supernova이다.
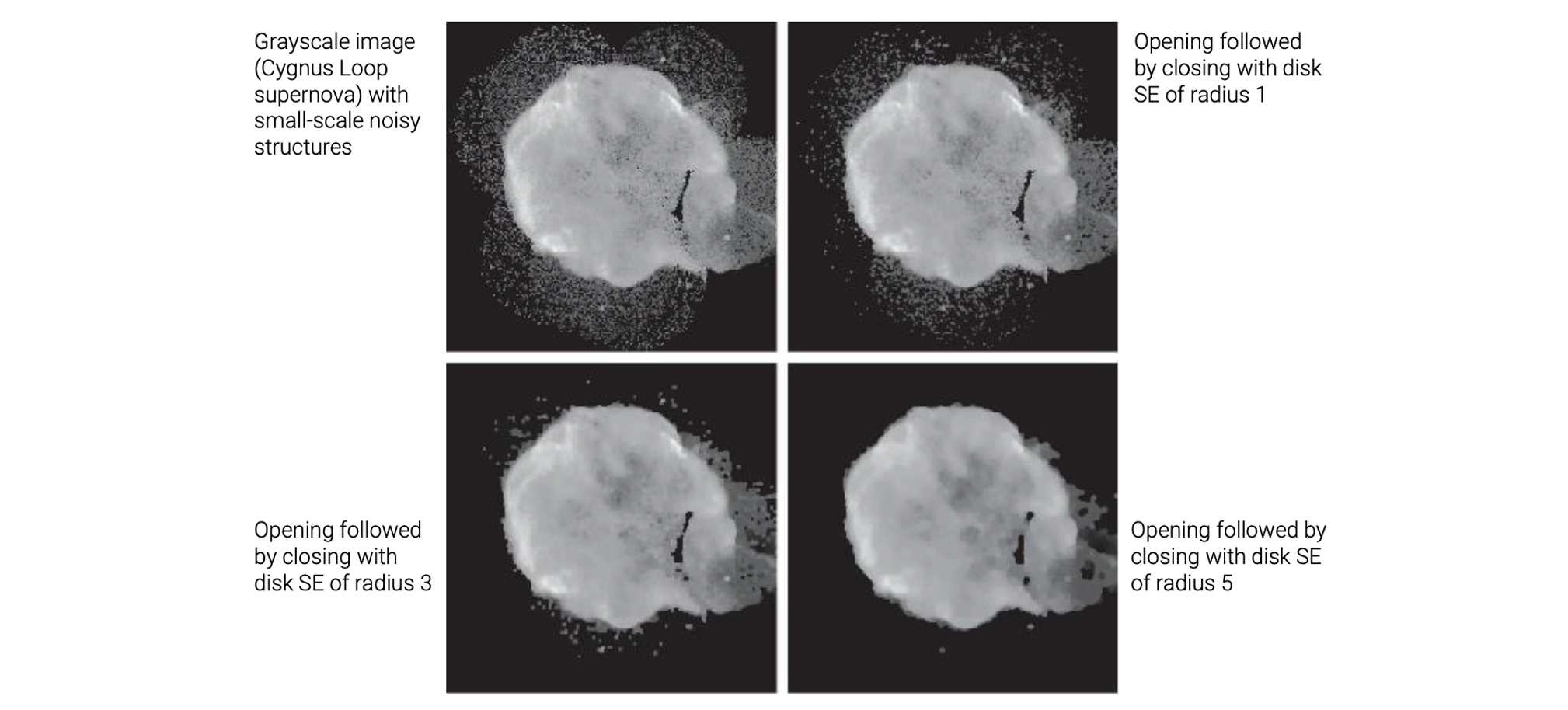이 예시에서 많은 수의 작은 noise들을 볼 수 있다. 그래서 opening과 closing을 이용해서 작은 크기의 하얀 점들과 검은 점들을 없애려고 한다. 그 결과 sturucturing element의 반지름의 크기가 가장 큰 경우가 성공적으로 noise들을 없앤 것을 볼 수 있다.