[계산사진학] Filtering in Frequency Domain

Linearity

Fourier transform은 linearity를 가지고 있다. 즉, 2개의 signal의 linear combinationd의 Fourier transform이 다음과 같이 있고 이를 2개의 Fourier transform의 linear combination으로 나타낼 수 있다.

이러한 성질은 DFT로 설명이 가능하다. DFT는 discrete Fourier transform의 약자로, digital 이미지에서의 discrete signal에 대한 Fourier transform을 이야기한다. DFT는 벡터 공간에서의 linear transform으로 설명이 가능해진다.

$x$는 spatial domain에서 $N\times N$ 이미지를 나타내는 $N^2$ 차원의 벡터로, 벡터 element는 이미지에서의 픽셀 값에 대응된다. 이미지의 사이즈때문에 element의 개수가 정해지게 된다. $y$는 $x$의 $N\times N$ DFT를 나타내는 $N^2$ 차원의 벡터이다. 그래서 $x$가 image $I$를 나타내면, $y$는 Fourier transform $F(I)$를 나타내게 된다. 마지막으로 $F$는 $N^2\times N^2$ 차원의 DFT 행렬을 나타낸다. 그래서 $F$는 선형대수 이론에서 배운 linearity property를 가지게 된다. $F$의 row vector들은 basis로서 각각의 sin function에 대응된다.

Periodicity of 2-D DFT

Fourier transform은 input에 주기 함수라는 가정을 포함한다. 이미지의 DFT를 계산할 때, 다음과 같은 이미지가 있다고 해보자.
이 이미지는 사실 주기 함수는 아니다. 하지만 실제로 DFT 자체는 input으로 무한히 반복되는 이미지를 전제하고 있다. 그래서 input 이미지는 실제로는 주기적이지 못하더라도, 반복되는 무한한 이미지를 가정하게 된다.
하나의 이미지가 가로, 세로 방향으로 무한히 있다고 생각하면 된다. 그래서 input 이미지의 크기는 무한히 크커지게 된다.
이러한 periodicity는 심지어 DFT 결과가 유한한 크기가 되어도 설명할 수 있다. Input 이미지의 크기가 $N\times N$이고 여기에 Fourier transform을 적용하면 같은 크기의 결과가 나오게 된다. 그리고 이 과정에서 시행된 Fourier transform은 무한한 크기로 가정하지만 유한한 크기에 적용이 된 것이다. 만약 정의상 Fourier transform에서 sin funtion과 cos function이 같은 값을 가지게 되면, 계속해서 무한하게 반복되게 된다.

Conventional Display for 2-D DFT

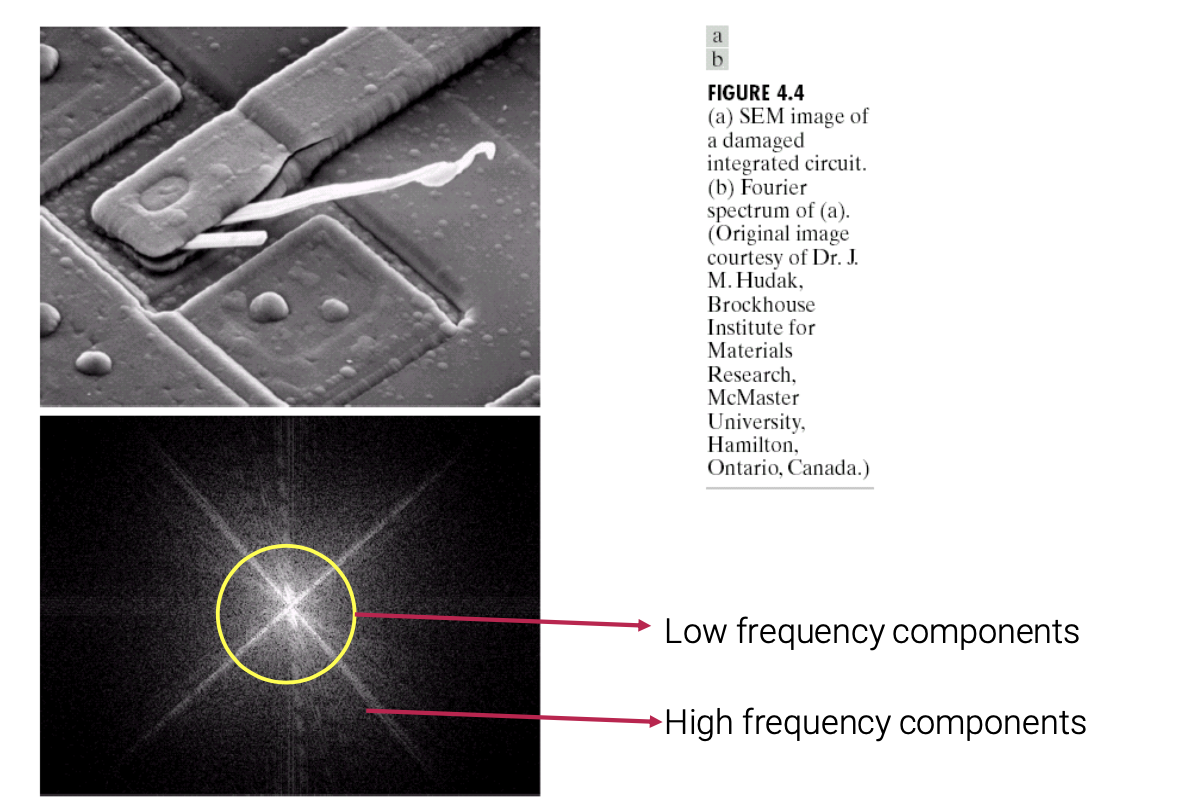
OpenCV나 numpy 등과 같은 라이브러리부터 image processing을 진행할 때 DFT를 사용하게 되면, 그 결과에서는 다음과 같이 외곽에는 low frequency component가 위치하고 중심부에는 high frequency component가 위치하게 된다.
하지만, 이러한 방식은 해석하기에 어려움이 존재한다. 그래서 visualization의 목적에 있어 더 쉬운 해석을 위해서 종종 0 frequency를 외곽이 아닌 중심부에 위치하도록 shift해주게 된다.
이러한 것은 오직 visualization을 위해서 행하는 것이다. 그렇다면 이러한 방법이 왜 가능할까? 그 이유는 위에서 말한 것과 같이 무한히 반복된다는 가정이 있기 때문이다.
그러면 이제 frequency domain에서 visualization 한 것을 예시로 보도록 하자.
좌측의 이미지는 spatial domain에서의 이미지이다. 그리고 우측의 이미지가 좌측의 이미지의 Fourier transform이다. 이미지의 중앙부에는 low frequency component가 위치한 것을 볼 수 있다. 이러한 visualization을 얻기 위해서는 FFT shift를 진행해서 signal을 shift해줘야 한다. 원본 이미지를 보면은 두드러지게 edge들이 수직과 평행으로 나타나 있는 것을 볼 수 있다. 그렇기 때문에 frequency domain에서 하얀색 선을 볼 수 있는 것이다. Spatial domain에서 1시에서 7시 방향으로 edge가 강하게 존재한다면, 이는 frequency domain에서 10시에서 4시로 수직으로 존재하게 된다. 다른 예시도 보도록 하자.
마찬가지로 원래 이미지와는 수직 방향으로 frequency domain이 만들어지는 것을 확인할 수 있다.

Filtering in the Frequency Domain

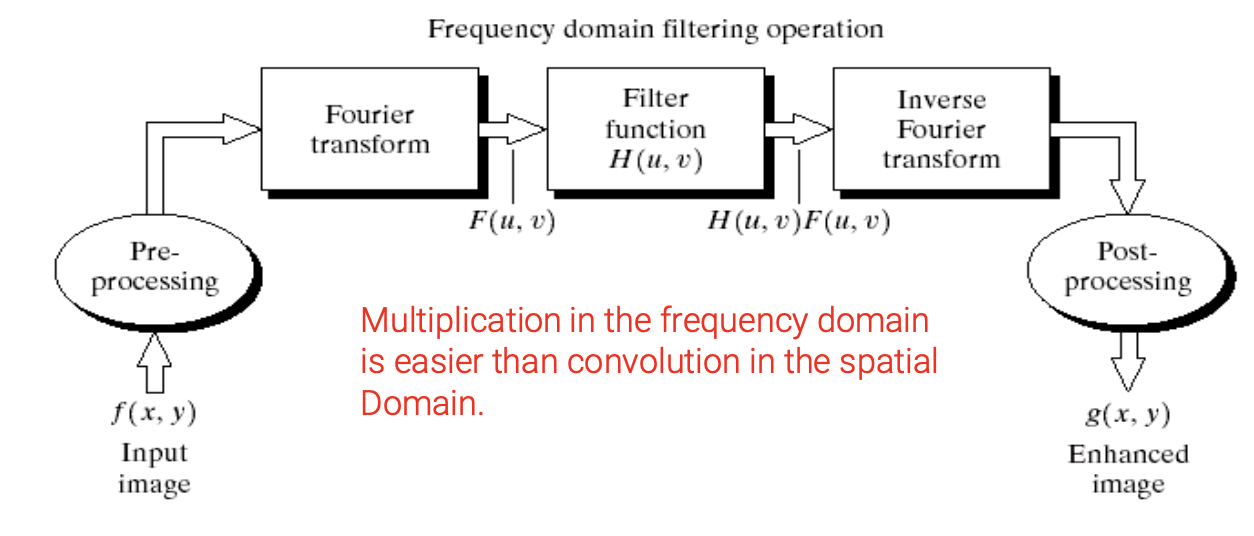
앞서 Fourier transform property에서 보았듯이 spatial domain에서의 signal간의 convolution operation은 frequency domain에서의 elementwise multiplication과 같아지게 된다.

그래서 우리는 spatial domain에서 convolution operation을 바로 하는 것이 아니라 다음과 같은 filtering process를 통해서 frequency domain에서 같은 일을 할 수가 있다.

Circular Convolution

사실 convolution theorem은 오로지 특별한 경우에만 사용이 된다. 앞서 Fouriere transform은 무한히 반복되는 signal에 대해서 성립한다고 이야기했다. 그래서 frequency domain에서의 filtering은 circular convolution은 만들어낸다. 무슨 의미인지는 다음 이미지를 통해 알아보도록 하자.
위와 같이 이미지와 convolution kernel이 있다고 해보자. 만약 이 이미지와 kernel로 convolution operation을 한다고 했을 때, 어떠한 종류의 padding이 수반되게 된다. 즉, spatial domain에서 convolution을 하고 싶다면, 이미지의 크기를 보존하기 위해서 padding이 필요하다는 것이다. Padding의 종류는 굉장히 많다. 그 중에서 frequency domain에서 convolution을 수행하기 위해서 쉽게 convolution theorem을 적용하고 싶다면 다음의 이미지가 결과로 얻게 될 것이다.
이 이미지는 convolution theorem을 사용해서 filtered 된 결과이다. 원래의 이미지를 $I$라 하고, kernel을 $f$라고 했을 때, $F^{-1}(F(I)\cdot F(f))$ 연산을 통해서 위의 결과를 얻게 될 것이다. 결과를 자세히보면 외곽이 어둡게 보이는 것을 확인할 수 있다. 외곽의 pixel이 low intensity 값을 가지고 있기 때문이다. 그렇다면 왜 low intensity 값을 가지게 된 것일까? 하늘은 원래 high intensity 값을 가져야 정상이다. 그 이유는 DFT에서 이야기했듯이 무한히 반복되는 이미지 $I$로부터 결과를 얻게 되는데, 그렇기 때문에 원래 이미지의 아래 부분인 어두운 배경의 영향을 받아서 하늘이 어두워지게 된 것이다.

그래서 circular convolution이라는 것은 convolution을 위해서는 이미지 모서리에 padding이 필요하게 되는데 이때 다음과 같이 이미지를 반복적으로 사용하여 padding의 효과를 내는 것을 말한다.
즉, frequency domain에서의 filtering은 이러한 circular convolution과 같다.

Lowpass and Highpass Filters

Fourier transform을 사용해서 이미지를 다른 frequency component로 분해할 수 있다. 이를 기반으로, frequency domain에서 lowpass filter와 highpass filter를 만들 수 있다. 다음과 같이 이미지가 있고, Fourier transform을 계산해서 다른 frequency component들로 분해할 수 있다.
그러면 중심부는 low frequency component가 있고, 외곽부는 high frequency component가 있게 될 것이다. 이로부터 lowpass filter와 highpass filter를 만들면 된다.

Ideal Lowpass Filter

Ideal lowpass filter는 다음과 같이 정의가 된다.

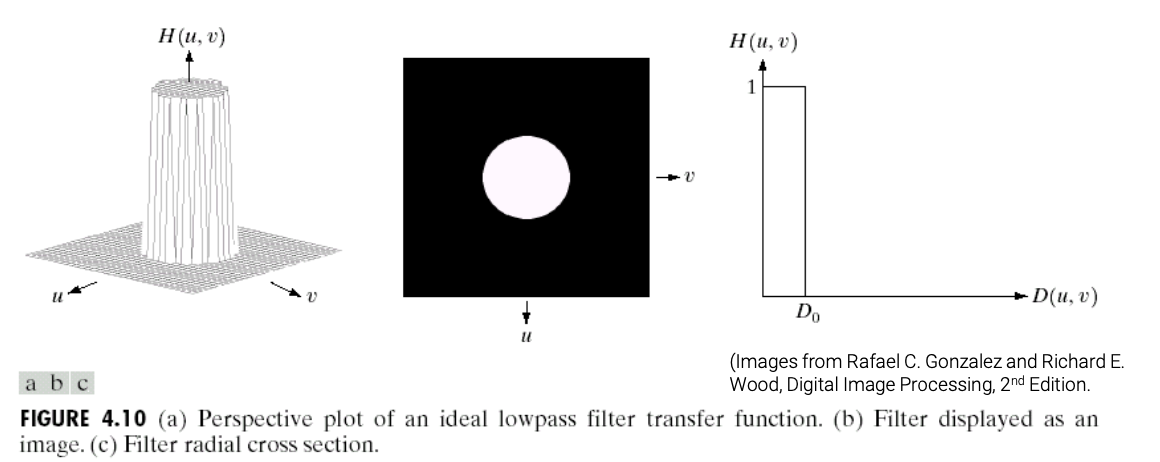Low frequency component는 특정 임의의 경계값보다 적은 값들로 이루어져 있다. 반대로 high frequency component는 특정 임의의 경계값보다 큰 값들로 이루어져 있다. 이렇게 만들어진 lowpass filter를 이미지와 계산을 시키게 되면 low frequency component는 유지하고 high frequency component는 무시하게 된다.

그리고 ideal lowpass filter에서 원의 크기는 우리가 low frequency component를 얼마나 보존하고 싶은지를 나타내게 된다. 원의 크기가 커지면 커질수록 더 많은 low frequency component를 보존하고 싶은 것이다. 반대로 원의 크기가 작아지게 되면 그만큼 low frequency component를 보존하고 싶지 않은 것이다. 다음은 lowpass filter의 원의 크기에 따른 결과를 보여주는 예시이다.

원래의 이미지가 있고, 서로 다른 ideal lowpass filter가 있을 때, lowpass filter의 크기에 따라 결과가 다르게 나타난다. Ideal lowpass filter에 있는 원의 크기가 작아지면 작아질수록, 더 많은 high frequency component를 버리게 된다. 그리고 결과적으로 더욱 blurry 이미지를 만들게 된다.

이에 대해서 보충 설명하자면, low frequency와 high frequency는 우선 딱 나눠 떨어지는 것이 아니다. 영상을 포함한 signal들은 다양한 frequency 성분들로 나누어 질 수 있고, 이 중에서 frequency가 상대적으로 낮은 성분들을 low frequency component, frequency가 상대적으로 높은 성분들을 high frequency component이라고 뭉뚱그려서 부르는 것 뿐이다. 영상과 같은 2D signal의 경우, Fourier transform을 한 후 visualization을 해 보면 Fourier transform의 중심에 일반적으로 가장 low frequency 성분이 표현되도록 visualization을 한다.그리고 바깥쪽으로 갈수록 점진적으로 frequency가 높아지는 성분들이 배치되게 된다. 그러니까 원의 크기가 작을 때는 일부의 low frequency component만 포함하다가, 원의 크기가 커질수록 점점 더 high frequency component들을 더 포함하게 되는 것이다. 그리고 원의 크기가 영상을 꽉 채우게 되면 low frequency component부터 high frequency component까지 포함하게 되는 것이다. 즉, 원의 크기가 작아지게 되면 정말로 low frequency component만 보존하게 되는 거고, 그것보다 frequency가 높은 component들은 다 버리게 됩니다. 그런데 영상의 디테일은 high frequency component에 있으니 점점 더 블러리한 이미지가 만들어지게 되는 것이다.

그리고 중간의 결과중에서 자세히보면 글씨 주변으로 물결모양의 울림 모양이 보이게 된다. 이를 ringing effect라고 한다.

How Rining Effect Happens

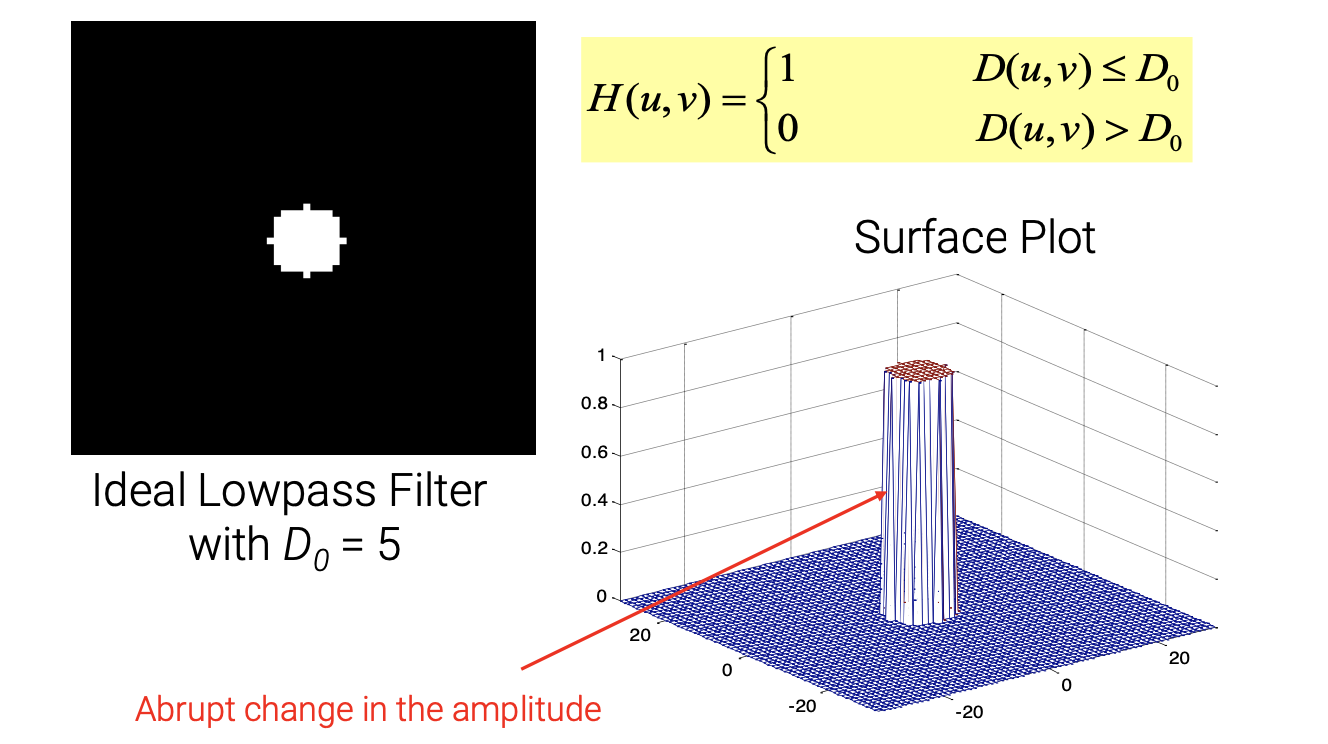위와 같은 ideal lowpass filter가 있다고 해보자. Frequency domain에서 이러한 ideal lowpass filter를 사용하게 되면 이에 대응하는 convolution kernerl이 반드시 존재하게 된다. Ideal lowpass filter에 대응되는 convolution kernel을 찾기 위해서 이 frequency domain filter에 inverse Fourier transform을 사용할 수 있다. 그러면 대응되는 spatial domain filter kernel를 다음과 같이 얻을 수 있다.
위의 spatial filter를 보면 마찬가지로 이상한 물결 모양이 보이게 된다. 그리고 이러한 물결 모양은 ringing effect를 만들게 된다.

Gaussian Lowpass Filter

이러한 물결 모양을 막기 위해서 보통 Gaussian lowpass filter를 사용하게 된다. Frequency domain에서 Gaussian lowpass filter는 다음과 같이 정의되고, 이를 visualization하면 다음과 같다.

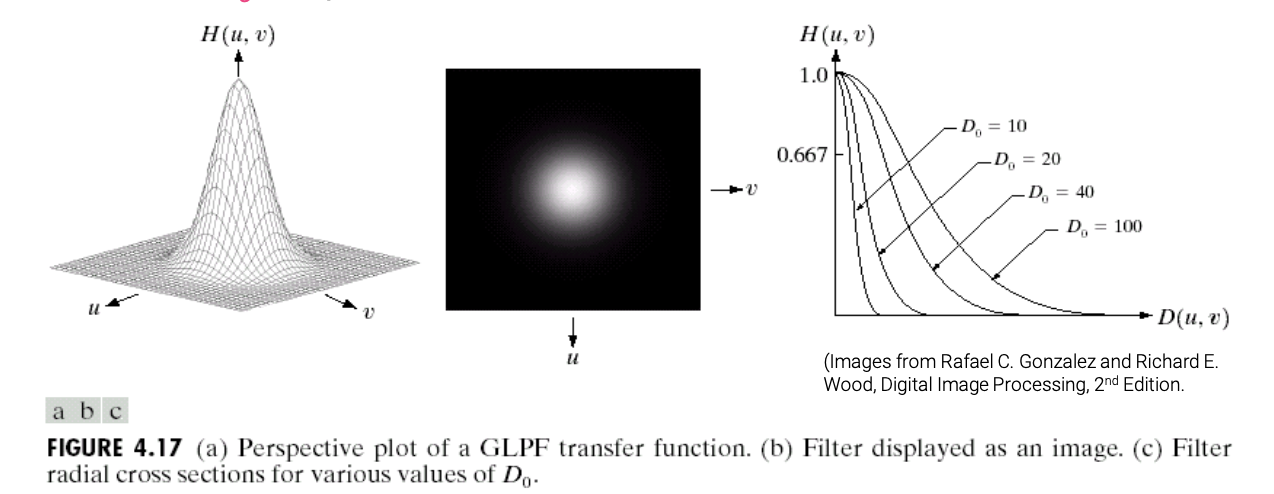중요한 점은 Gaussian filter만이 물결 모양을 가지고 있지 않고, 그렇기에 ringing effect 또한 없다.
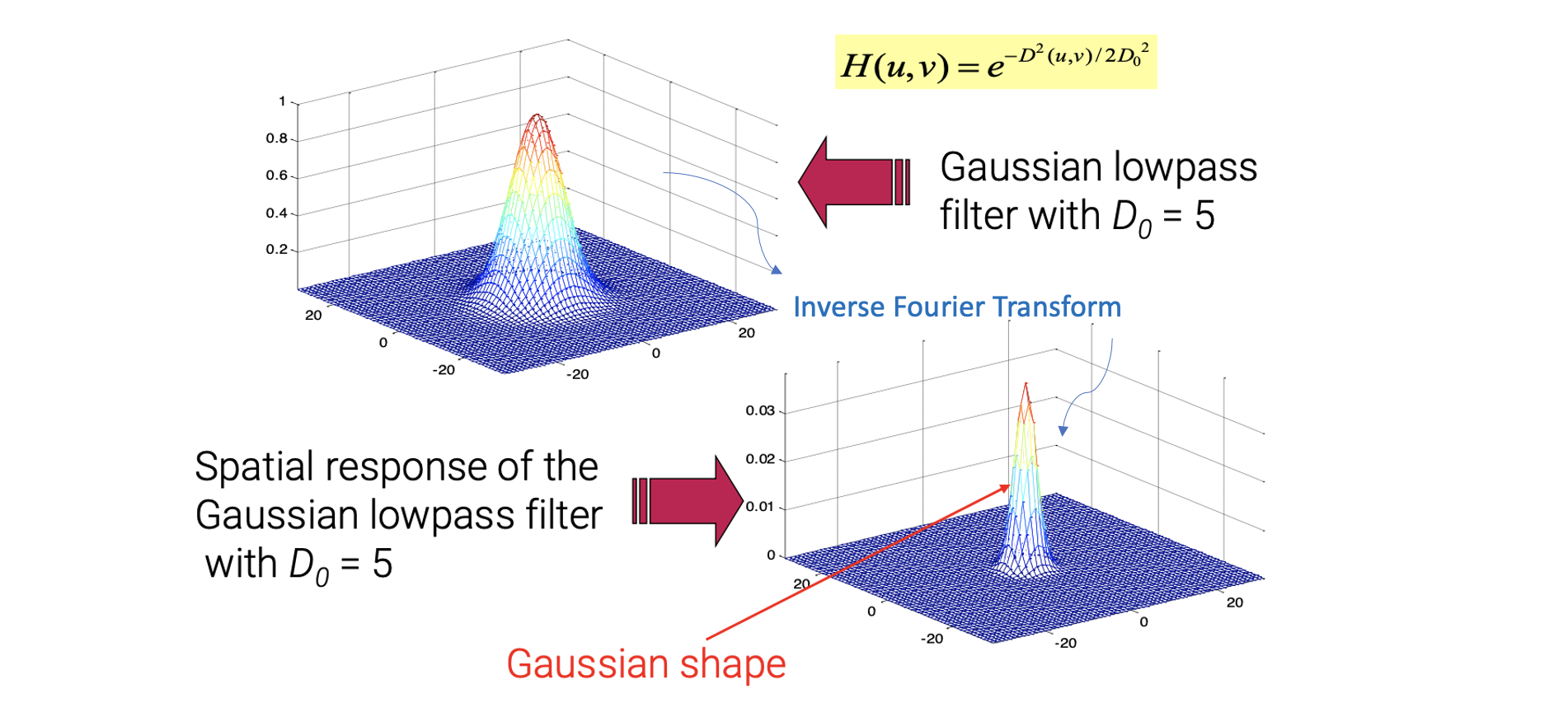Frequency domain에서의 Gaussian lowpass filter에 inverse Fourier transform을 계산하면 또 다른 모양의 Gaussian lowpass filter를 만들 수가 있다. 그리고 이 Gaussian filter는 spatial domain으로 바뀌게 된다. 그리고 spatial domain에서 Gaussian lowpass filter는 어떠한 물결 모양도 존재하지 않게 된다. 그렇기 때문에 ringing effect를 없애기 위해서 Gaussian filter를 이용하는 것이다.

Highpass Filter

그렇다면 highpass filter는 어떠할까? Frequency domain에서의 highpass filter는 lowpass filter로부터 쉽게 유도가 가능하다. 다음 식에서 1은 frequency domain에서의 constant function이다.

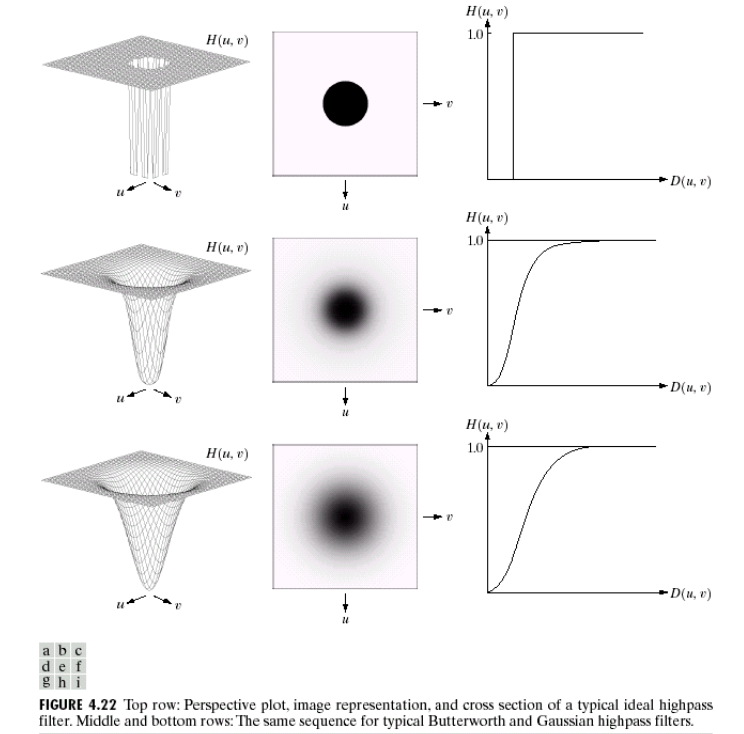
Ideal Highpass Filter

Ideal highpass filter의 정의는 다음과 같다.

Ideal lowpass filter로부터 유도를 할 수 있기 때문에, 결과가 반대가 된다.

Gaussian Highpass Filter

Gaussian highpass filter 또한 Gaussian lowpass filter로부터 유도하면 된다.

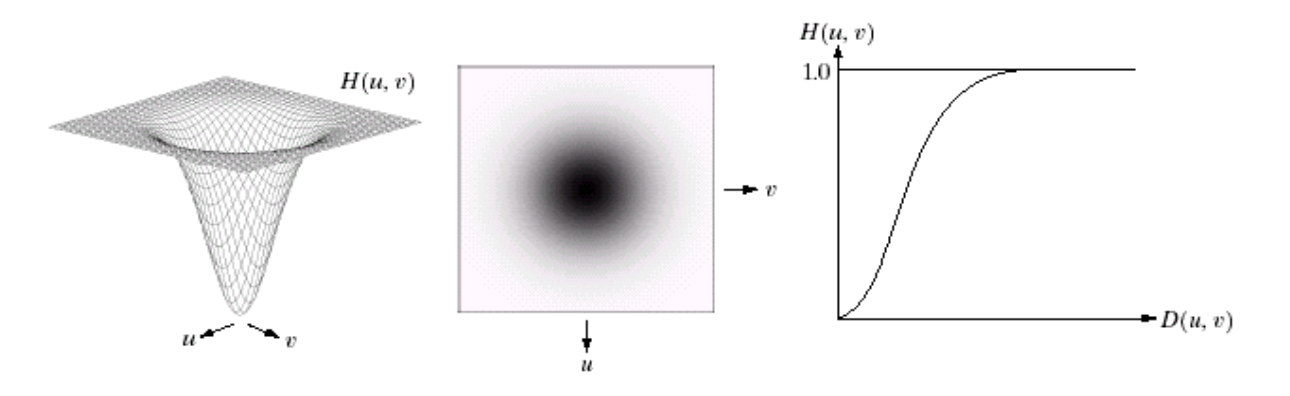
Spatial Responses of Highpass Filter

Ideal lowpass filter와 비교했을 때, Ideal highpass filter는 또한 물결 모양을 가지고 있다. 그러나 Guassian highpass filter는 이러한 물결 모양을 전혀 가지고 있지 않다. 그래서 ringing effect 또한 없게 된다.

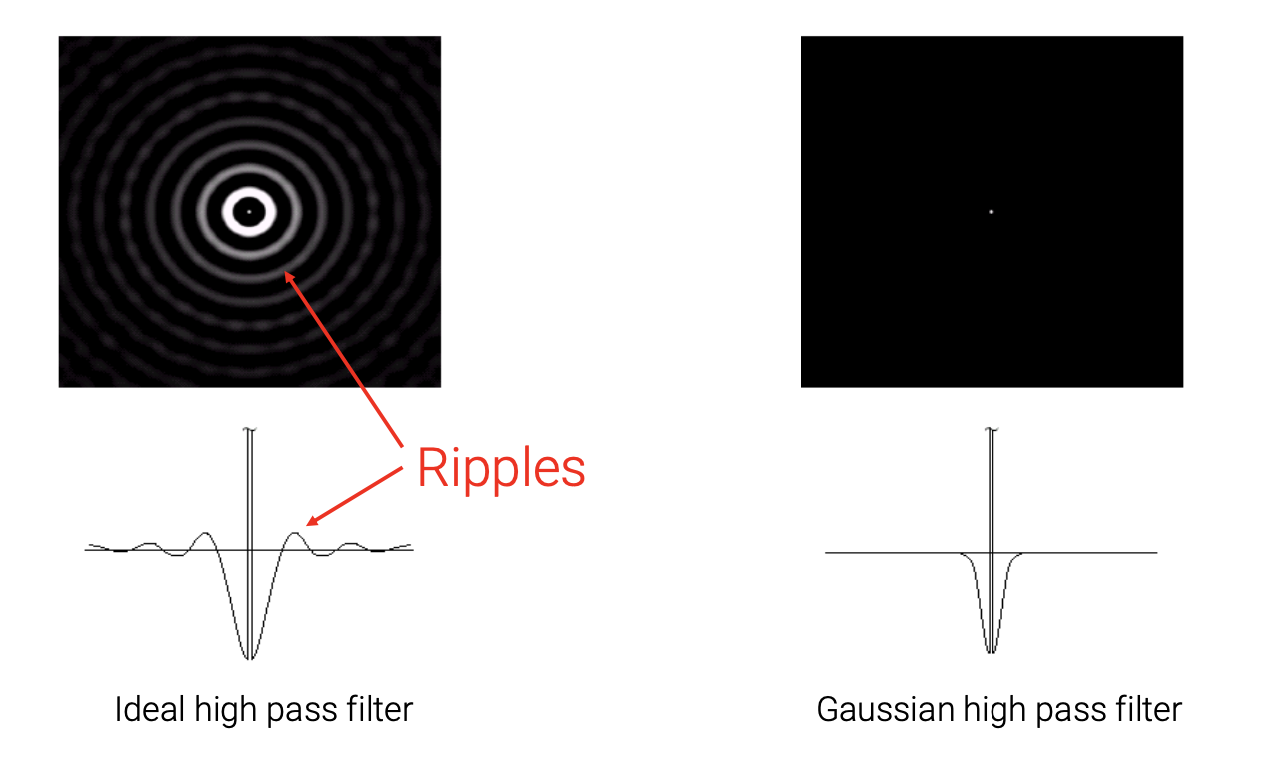
Results of Ideal Highpass Filters

Results of Gaussian Highpass Filters

이러한 이유 때문에 Ideal highpass filter보다 Gaussian highpass filter를 사용하는 것이다. 그렇다면 ideal lowpass/highpass filter는 왜 사용하는 것일까? 그 이유는 filter가 접근하기에 가장 단순하기 때문이다. Low frequency component를 유지하려면 high frequency component를 없애야하는데, 이러기 위해서는 특정 경계값을 설정해주게 되는데, 이러한 기본적인 아이디어가 ideal filter에 사용되게 된 것이다. 그래도 이 filter가 효과적이라고는 할 수 없다.