[계산사진학] Frequency Domain 2

이전까지 Fourier transform의 정의와 특징에 대해서 알아보았다. 지금부터는 convolution theorem에 대해서 알아볼 것이다.

Convolution Theorem

Convolution theorem은 두 함수로부터 convolution의 Fourier transform은 각각의 Fourier transform의 곱이라는 것을 말한다.

여기서 convolution은 spatial domain에 속하며, 이는 frequency domain의 곱과 같다는 것을 말하고 있다. 다음 예시를 보도록 하자.
$f(x,y)$는 input image이고 $h(x,y)$는 convolution kernel로 여기서는 Gaussian kernel이 사용되었다. 이 둘을 convolution을 진행해주면 $g(x,y)$를 얻을 수 있게 된다. 그러면 이번에 우측의 이미지를 보자. 우측의 이미지들은 전부 대응되는 좌측의 이미지로부터 Fourier transform을 통해서 얻은 Fourier spectra이다. $|F(S_x,S_y)|$와 $|H(S_x,S_y)|$는 각각 Fourier transform의 결과고 이를 곱하게 되면 $|G(S_x,S_y)|$가 나오게 된다. 이때, $g(x,y)$와 $|G(S_x,S_y)|$는 서로 forward, inverse 방향으로 Fourier transform을 진행해주면 얻을 수 있다. 이것이 2D 이미지로 convolution theorem을 보이고 있는 것이다.

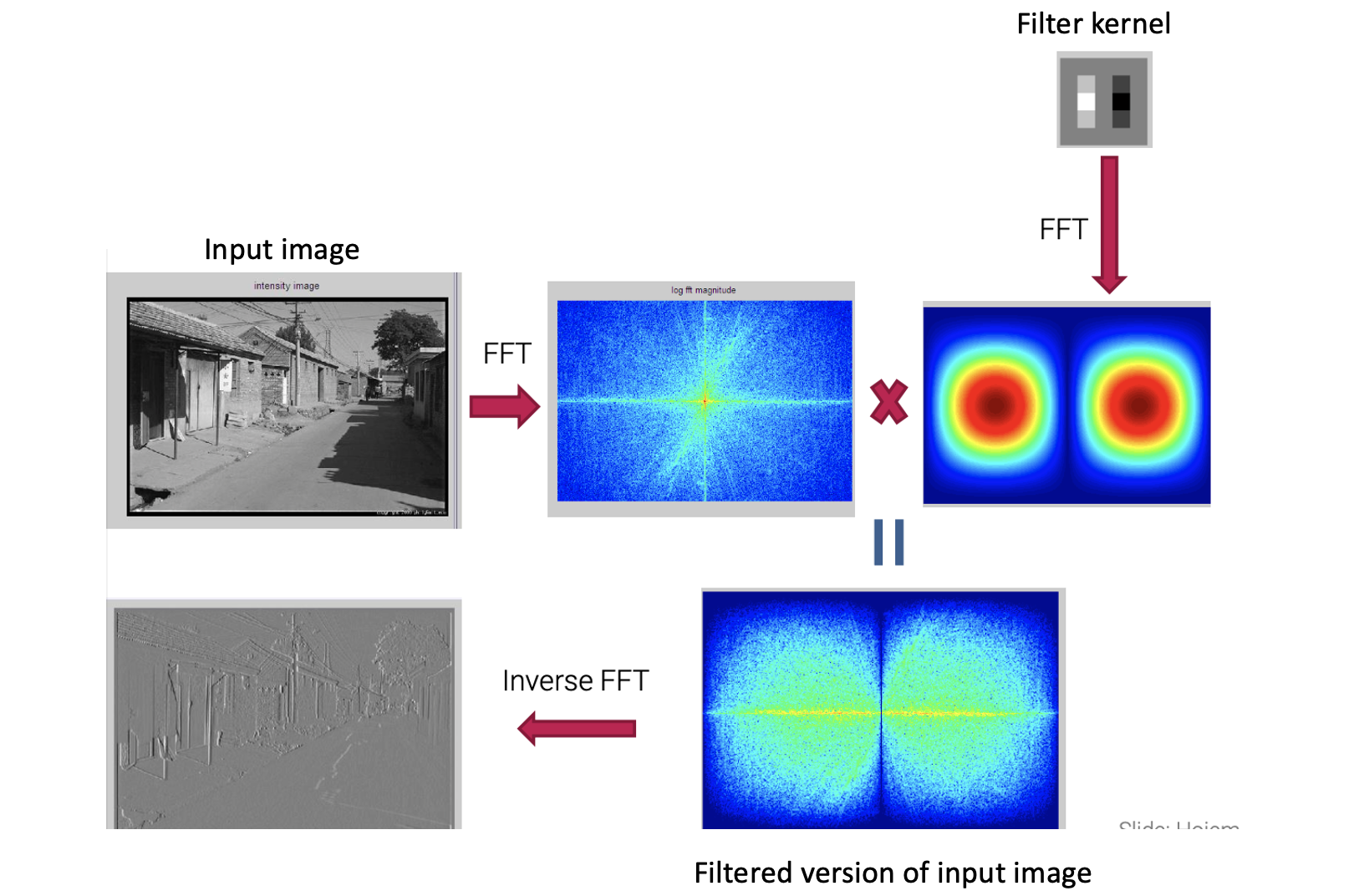그래서 이 theorem을 이용하면 위와 같이 적용할 수 있다. 우선 input image와 kernel을 준비해서 각각의 Fourier transform 결과를 만든다. 그리고 이 결과들을 곱하게 되면 input image의 filtering 된 결과가 나오게 되고, 여기에 inverse Fourier transform을 통해서 input image와 kernel의 convolution 결과가 나오게 된다. 여기서 알 수 있는 사실은 간단하다. 원래는 convolution 연산을 spatial domain에서 진행하게 된다. 그런데, 이 spatial domain에서 convolution 연산을 직접적으로 계산하기 보다는, 각각을 Fourier transform을 이용하여 frequency domain에서의 곱셈 연산을 통해서 같은 결과를 얻을 수 있게 된다.

Convolution 연산을 진행하면 되는데 왜 굳이 convolution theorem을 이용하는가? 바로 computional efficiency 때문이다. 물론, 몇가지 경우에 대해서는 convolution 연산을 직접 수행하는 것이 더 효과적일 수 있다. 그래도 더 효과적일 수도 있기 때문이며 설명을 보도록 하자.

N 픽셀의 input 이미지 $f$와 M element의 filter $h$가 있다고 하자. 이 둘의 convolution 연산은 $f * h$이고, spatial domain에서의 둘의 convolution에 대해서 time complexity는 O(MN)일 것이다. 그렇다면 frequency domain에서는 어떠할까? Frequency domain filtering은 $F^{-1}[F[f]F[h]]$가 되는데, 각각의 Fourier transform을 element-wise multiplication을 진행해주고 이를 다시 inverse Fourier transform을 진행하게 된다. 이 과정에서 2D Fourier transform time complexity는 O(NlogN)이 된다. 그래서 total time complexity는 2번의 forward Fourier transformation, 1번의 inverse Fourier trnasformation, 그리고 N번의 곱셈 연산이 있어 $O(3NlogN + N) = O(NlogN)$이 될 것이다. 따라서, M이 커지게 되면 $O(NlogN)$보다 $O(MN)$이 더 커지기 때문에 spatial domain에서의 convolution 연산은 비효율적이게 된다.

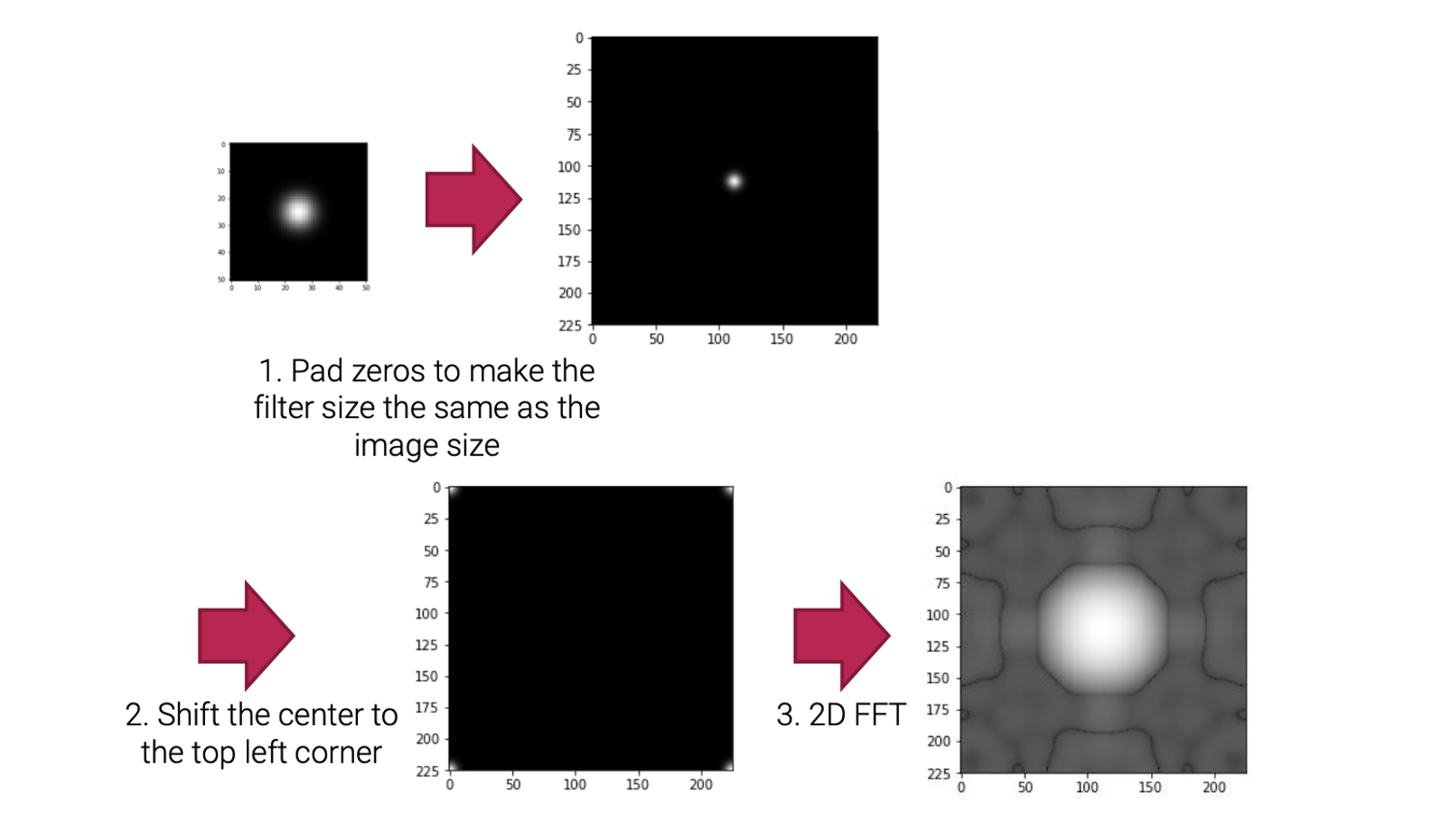만약에 frequency domain filtering을 하게 되었을 때는 padding과 shifting을 고려해줘야 한다. 보통은 input 이미지와 filter kernel의 convolution 연산은 진행하면 되는데, 각각을 Fourier transform을 하고 multiplication을 진행할 때 서로 크기가 다르면 진행할 수가 없다. 그래서 먼저 filter kernel을 input image의 크기와 같도록 외곽으로 0을 추가해주는 padding 작업이 필요하다. 그리고 제대로 된 결과를 얻기 위해서는 가운데 지점을 좌측 위로 이동시켜줘야 하는데, 이때 0이 아닌 값들을 순환하듯이 외곽으로 shifting 시켜줘야 결과가 제대로 나오게 된다. 그래서 padding과 shifting을 진행해주고 마지막에 Fourier transform을 해주게 되면 제대로 된 결과를 얻을 수 있다.

Spatial domain에서의 convolution 연산같은 경우 보통은 filter kernel의 center가 이미지의 center에 위치하게 하여 연산을 진행해준다. 하지만 frequency domain에서 Fourier transform을 진행해줄 때는 이미지의 원점에 대응되는 filter의 center를 고려해 줄 필요가 있다.

Frequency Analysis

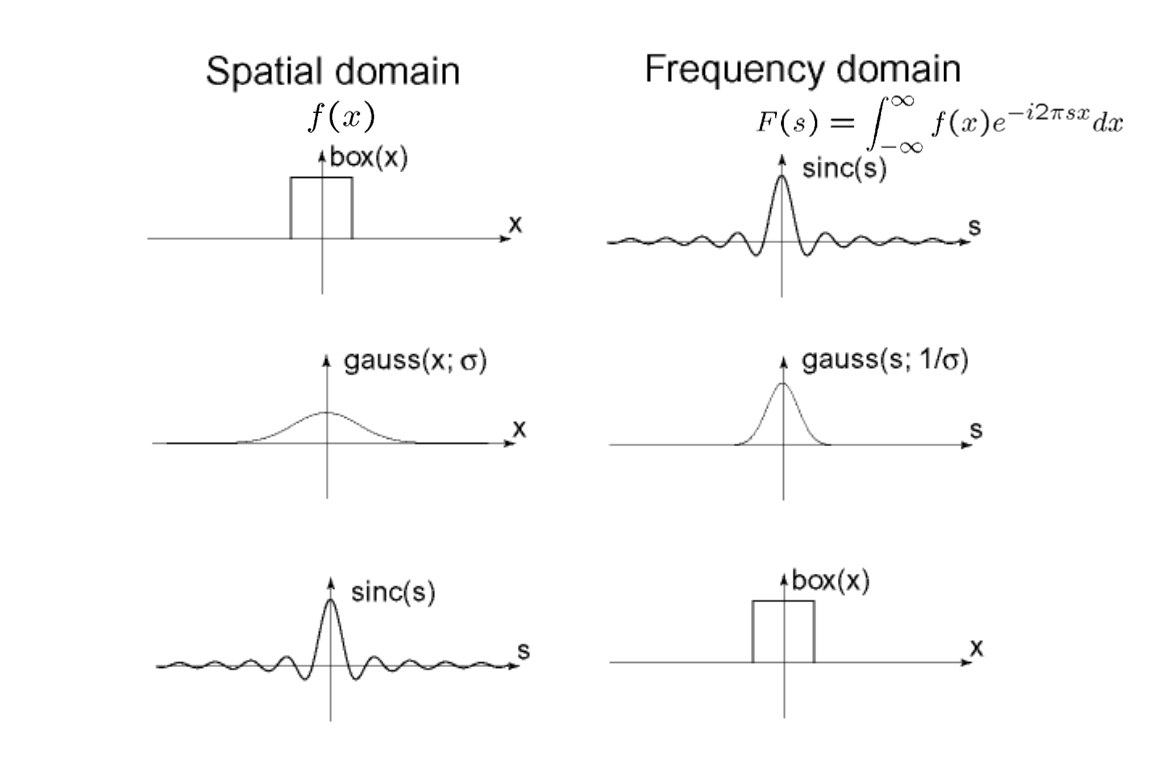
Fourier transform을 하게 되었을 때, 아무래도 수학적으로 흥미로운 사실들이 존재한다. 먼저 Fourier transform pair에 관한 것이다. 다음 예시들은 흥미롭게도 서로 역관계를 가지거나 모양만 바뀌고 자기 자신 그대로 나오는 경우들이다.
이전에 lowpass, highpass, bandpass filter가 무엇인지는 알아보았다.
먼저 lowpass filter를 알아보려고 한다. 특히 Gaussian lowpass filter에 대해서 알아볼 것이다. Gaussian filter는 Fourier transform을 진행해도 다른 모양의 gaussian filter를 만들게 된다. 그래서 filter의 중심은 lowest frequency component이고 가장 외곽의 값은 0이 될 것이다. 이러한 경우 frequency domain에서 high frequency를 지우는 역할을 하게 된다. 다음으로는 bandpass filter이다.
Bandpass filter는 특정 구간의 frequency만 통과시킨다. 그래서 low frequency component와 high frequency component를 지워버리게 된다. 그래서 이 filter를 이미지에 적용하면 low frequency가 제거되고 디테일한 부분도 사라지게 되는 것을 볼 수 있다. 일종의 smooth한 디테일만 남게 된다.

Campbell-Robson Contrast Sensitivity Curve

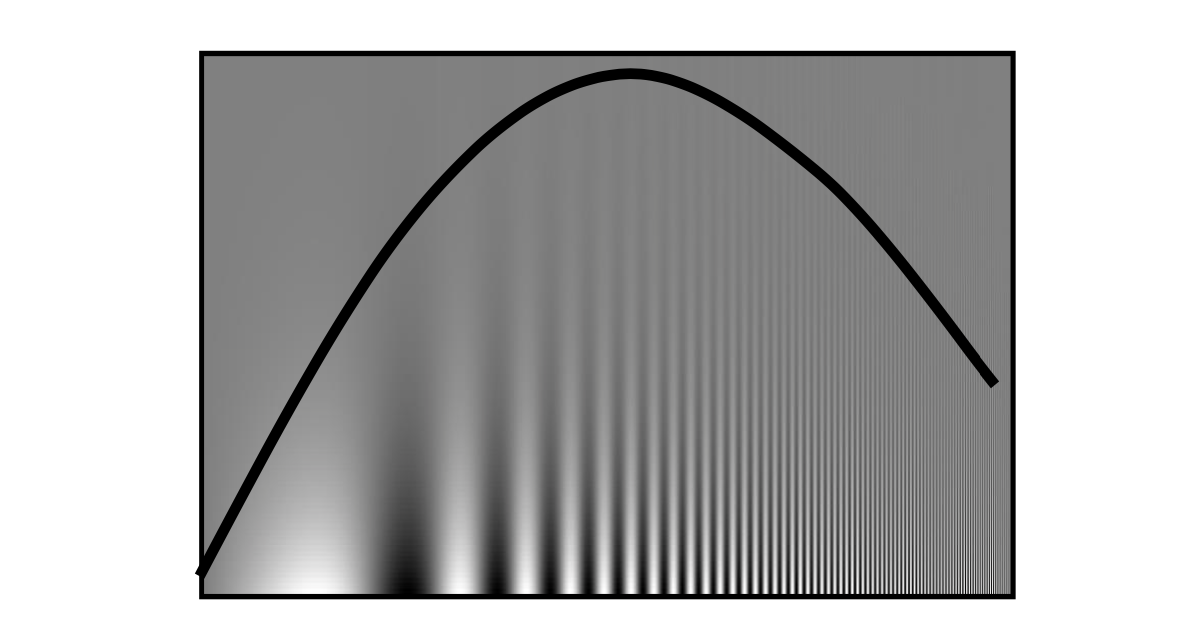실제로 사람 눈은 특정 frequency에 더 민감하다. 위의 이미지는 각기 다른 frequency를 시각화 한 것이다. 좌측으로 갈수록 low frequency이고, 우측으로 갈수록 high frequency이다. 그리고 위로 갈수록 magnitude가 크고 아래로 갈수록 magnitude가 작아지게 된다. 사람의 눈은 특정 구간에서 더 선명하게 보이게 된다. 그렇기 때문에 위와 같은 곡선에서 곡선을 기준으로 위보다는 아래 부분이, 가장 외곽보다는 중간 부분이 선명하게 보이는 것이다. 이러한 사실은 digital 이미지를 만드는데 똑같이 작용한다.

Depends on Color

또한 사람의 눈은 색의 요소에 따라 민감하게 작용한다. 위의 RGB이미지가 있다고 했을 때, 3개의 요소에 대해서 lowpass filter를 사용했다. 그리고 사람의 눈으로 보았을 때, 빨간색과 파란색의 이미지는 선명하게 보일 것이다. 그러나 초록색의 이미지는 smooth하게 보일 것이다. Lowpass filter를 모두 적용했는데 왜 이러한 차이가 있을까? 이러한 사실은 사람의 눈이 더욱 초록색의 channel에 있는 high frequency에 민감하게 반응한다는 것을 보여준다.

Lossy Image Compression(JPEG)

Lossy Compression은 JPEG 이미지를 만들 때 어느정도 정보를 손실해서 압축하는 방법을 이야기한다. 다음과 같이 이미지가 있다고 하자.
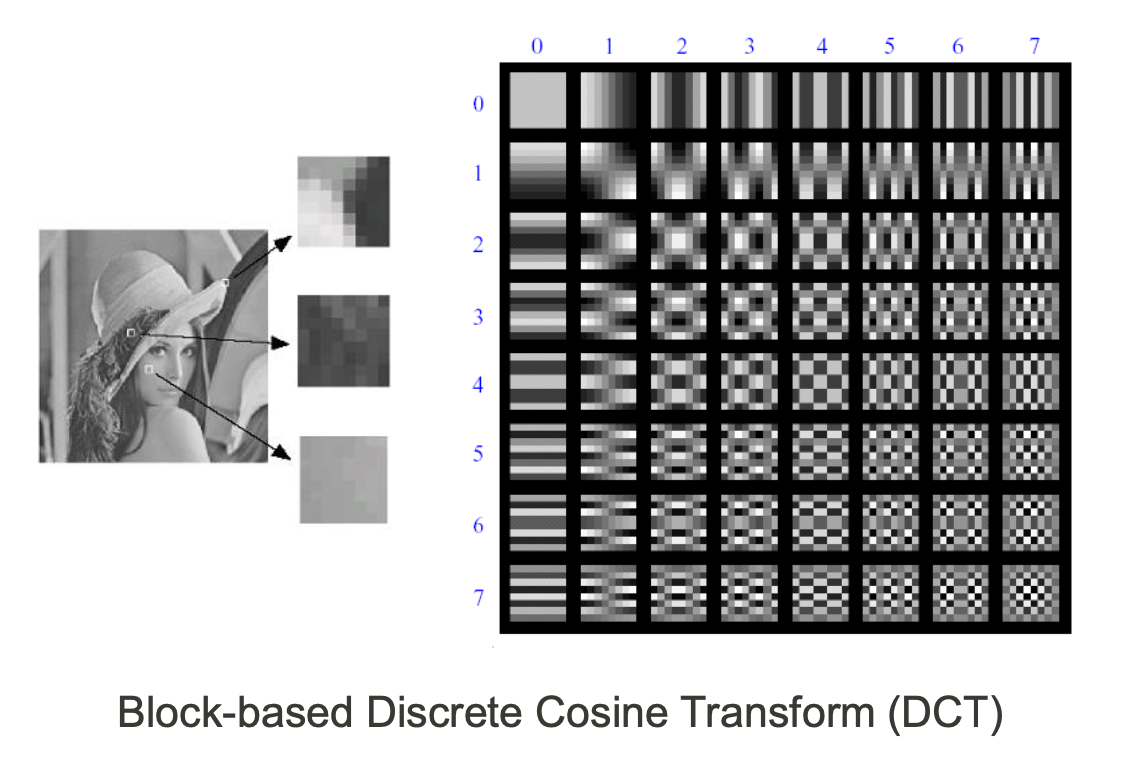이 이미지를 $8\times 8$ patch들 여러개로 나눌 수가 있다. 그리고 이 patch들에 discrete cosine transform(DCT)를 이용할 것인데, Fourier transform 대신이기는 하지만, 다른 frequency component로 분해한다는 점은 비슷하다. 그래서 DCT를 이용해서 low frequency component부터 high frequency component까지 분해할 수 있다.
DCT를 이용하게 되면 벡터에서 basis의 개념과 비슷하게 여러개의 frequency component와 그 가중치를 얻게 된다. 그래서 기존의 patch를 64개의 coefficient로 설명이 가능해지게 된다. 앞서 사람의 눈이 high frequency에 덜 민감하다는 것을 알게 되었다. 그렇기 때문에 high frequency를 없애도 사람의 눈에는 결과가 크게 달라지지 않게 된다. 그래서 64개의 coefficient보다 적은 32개나 16개로도 충분히 기존의 patch를 대변할 수 있게 된다. 다음이 그 예시이다.
사람의 눈에는 두 이미지가 크게 다른점이 보이지 않을 것이다. 하지만 우측의 이미지는 high frequency component를 상당수 제거한 결과이다. 그렇기 때문에 JPEG 이미지를 만들 때 lossy compression을 이용하게 되는 것이다.

Frequency domain에 대해서 공부할 때 놓치지 말아야 하는 점은 다음과 같다.

1. 이미지와 filter의 계산에 있어서 spatial domain도 좋지만 frequency domain도 고려해 볼 필요가 있다.
2. Filter의 사이즈가 커지면 커질수록 Fourier transform의 효율성은 더욱 커지게 된다.
3. 사람의 눈은 high frequency에 대해서는 덜 민감하기 때문에 이를 생각해 둘 필요가 있다.