[계산사진학] Frequency Domain 1

이미 frequncy가 무엇인지에 대해서는 잘 알고 있을 것이다. 1차원에서의 signal과 2차원(이미지)에서의 signal이 무엇인지는 이미 알아보았다. 1차원에서의 signal은 느리게 흘러가는 low frequency component와 빠르게 흘러가는 high frequency component로 분해가 가능하다. 이러한 분해는 2차원 이미지에서도 가능하다. 원래의 digital 이미지가 있다고 생각해보자. 그러면 이 이미지를 서로 다른 지점의 픽셀 값이 느리게 변하는 low frequency component와 서로 다른 지점의 픽셀 값이 빠르게 변하는 high frequency component로 분해가 가능하다.

그래서 frequncy domain image processing은 이미지를 서로 다른 freqency component로 분해가 가능한 것을 의미하게 된다. 이러한 과정 속에서 유의미한 결과를 도출해낼 수 있다. Image anaylsis, image enhancement, computational efficiency, image compression과 같은 목적에 유용하게 사용이 된다. 다음의 흥미로운 예시를 살펴보자.

위의 그림은 Salvador Dali가 그린 그림 중 하나이다. 이 그림이 흥미로운 이유는 Dali가 frequncy를 이용해서 그림을 표현했기 때문이다. 원본 이미지를 보면 한 여자가 서 있는 평범한 그림처럼 보인다. 하지만 이 이미지를 lowpass filter를 이용해서 low frequency component만 살피게 되면 여자의 모습은 더이상 보이지 않고 Abraham Lincoln의 초상화가 얼핏 보이게 된다. 반대로 highpass filter를 이용해서 high frequency component만 보게 되면 여자의 모습이 더욱 선명하게 보인다. 작가는 서로 다른 frequency를 이용해서 이러한 흥미로운 작품을 그리게 되었다.

Fourier Transform

1807년에 Joseph Fourier는 기가 막힌 아이디어를 가지고 있었다. 바로 "모든 주기 함수는 다른 주파수의 사인과 코사인의 가중 합으로 다시 쓸 수 있다" 였다. 그러나 그 당시에는 큰 지지를 받지 못하였고, 1878년까지도 영어로 전해지지 못했다. 하지만 이는 사실로 들어났고 오늘날의 Fourier Series가 되었다. 다음의 예시를 보도록 하자.

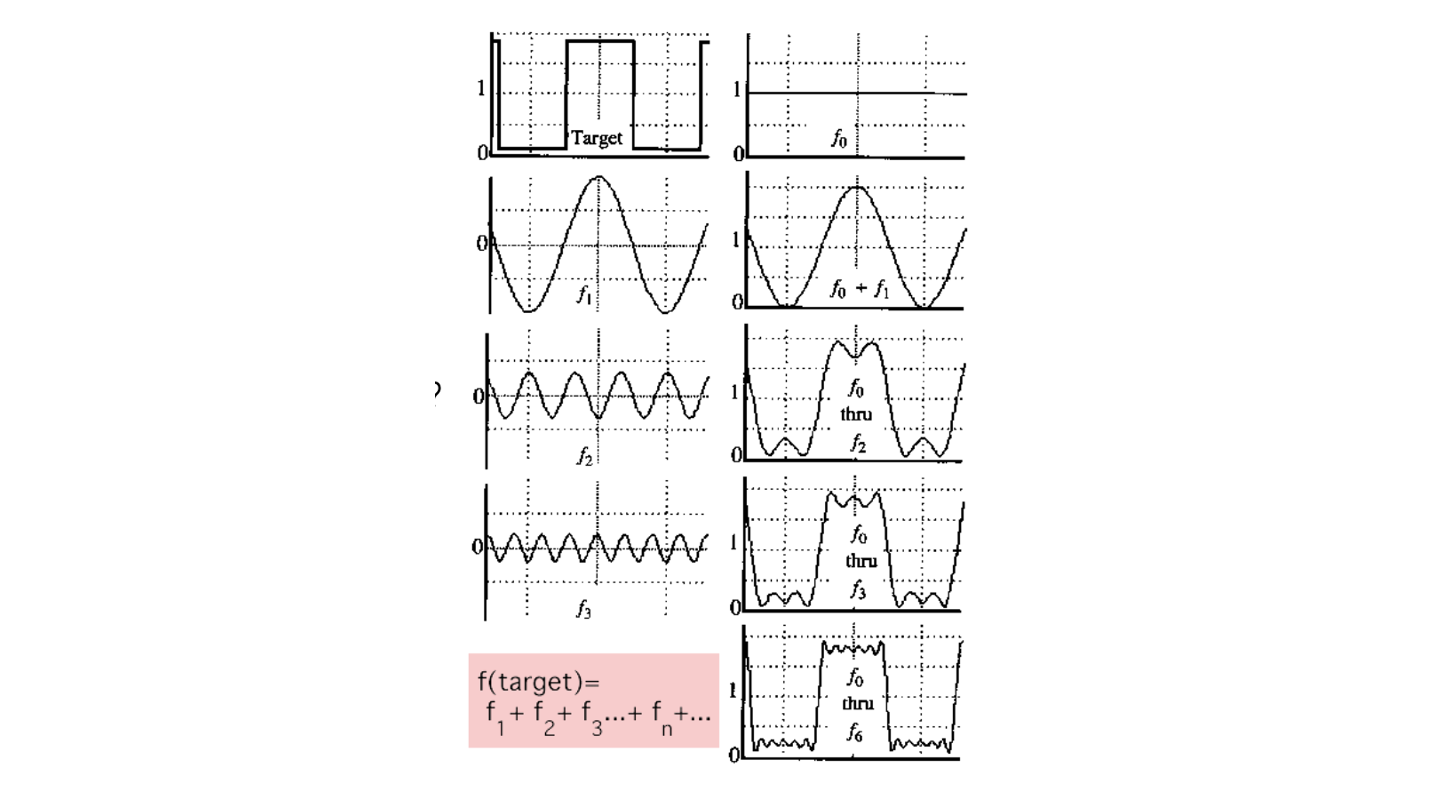Target function으로 어떠한 주기 함수가 있다고 하자. 우리의 목표는 다음과 같이 이 주기 함수를 어떠한 가중치의 합의 sin 함수로 바꾸는 것이다.

$A$, $\omega$, $\phi$의 값을 조절해가면서 이들의 합을 통해서 어떠한 signal도 만들어낼 수가 있다. 위의 targer function으로부터 만약에 $\omega$는 0, $A$는 1이라고 값을 설정하게 되면 $f_1$을 얻게 되고 $\omega$를 증가시켜서 $f_2$를 얻고 이를 합치게 되면 target function에 근사하는 결과를 만들어 낼 수가 있다. $A$, $\omega$, $\phi$의 값을 계속해서 바꿔나가고 조절해가다보면 우리는 계속해서 새로운 함수를 만들어낼 수가 있고 나중에는 target function과 거의 유사한 결과를 만들어 낼 수 있다. 이러한 아이디어가 바로 Fourier series이다.

위의 예시에서는 sin함수를 예시로 들어보았다. 그리고 이 sin 함수는 3개의 parameter를 가졌다. 이때, 이 함수의 degree of freedom은 3이 되고, 각각의 parameter들은 각기 다른 역할을 가지게 된다. $A$는 함수의 magnitude를 조절하게 된다. 값을 키우게 되면 함수가 위아래로 strech되어 함수의 모양이 변하게 된다. $\omega$는 함수의 frequency를 조절하게 된다. 그래서 처음에 0이었을 때 함수가 linear하게 형성되게 되는 것이다. 마지막으로 $\phi$는 phase를 조절하게 된다. 즉, 함수의 location에 관여하여 함수 자체를 좌우로 shift하는 역할을 한다.
그렇다면 이 3가지 parameter 중에서 signal의 모양을 coarse하거나 fine하게 만드는 주된 역할을 하는 것은 누구일까? 바로 $\omega$이다. $\omega$를 줄이게 되면 더 낮은 frequency를 만들게 되어 coarse한 signal 모양을 만들고 반대로 키우게 되면 더 높은 frequency를 만들게 되어 fine한 signal 모양을 만들게 된다.

그래서 예시를 통해서 우리는 어떠한 주기 함수도 sin 함수의 가중치의 합으로 표현이 가능하다는 것을 알게 되었다. 이를 식으로 살펴보면 다음과 같다.
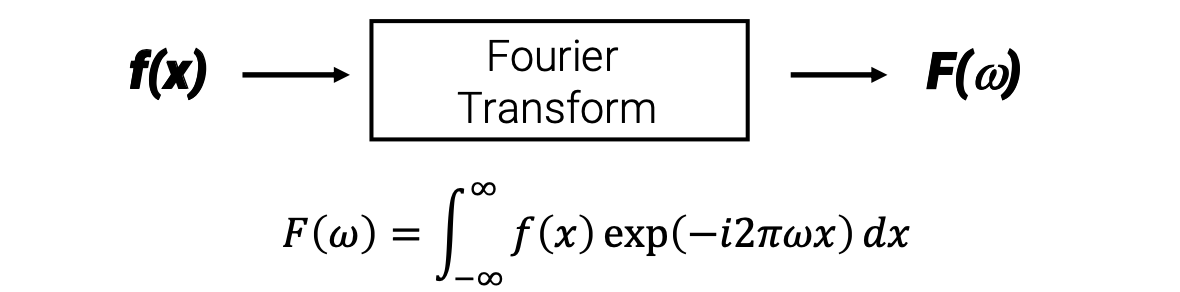위와 같이 원래의 주기 함수 $f(x)$를 Fourier transform의 식을 이용해서 $F(\omega)$를 얻을 수 있다. 이때 원래의 함수에서 parameter였던 $x$는 Fourier transform을 이용하게 되면 $\omega$로 바뀌게 된다. Frequency에 대응되는 $\omega$에 따라 Fourier transform을 이용하게 되면 그 결과는 complex number가 된다.

$F(\omega)$는 complex number인 $R(\omega) + iI(\omega)$로 표현이 되고, 이는 다시 $A(\cos(\phi) + \sin(\phi))$로 표현이 된다. 그리고 이 식은 다시 오일러 공식에 의해서 $Aexp(i\phi)$로 표현할 수 있다. 여기서 $A$와 $\phi$는 위와 같이 계산이 가능한데, 이를 각각 부르기를 $A$는 magnitude, spectrum이라 하고, $\phi$는 phase, phase angle, phase spectrum이라 한다. 그리고 $A^2$는 power spectrum, spectral density라 부를 수 있다.

그리고 반대로 Fourier transform value인 $F(\omega)$를 원래의 signal로 바꿀 수도 있다. 이때는 inverse Fourier transform 식을 이용하면 된다. 식이 비슷해보이나 parameter가 $x$에서 $\omega$가 된 것을 볼 수 있다.

Fourier transform을 이용해서 어떠한 signal을 서로 다른 frequency component로 분해가 가능하다. 그리고 각각은 sin 함수로 표현이 가능하게 된다. 다음의 예시를 보도록 하자.

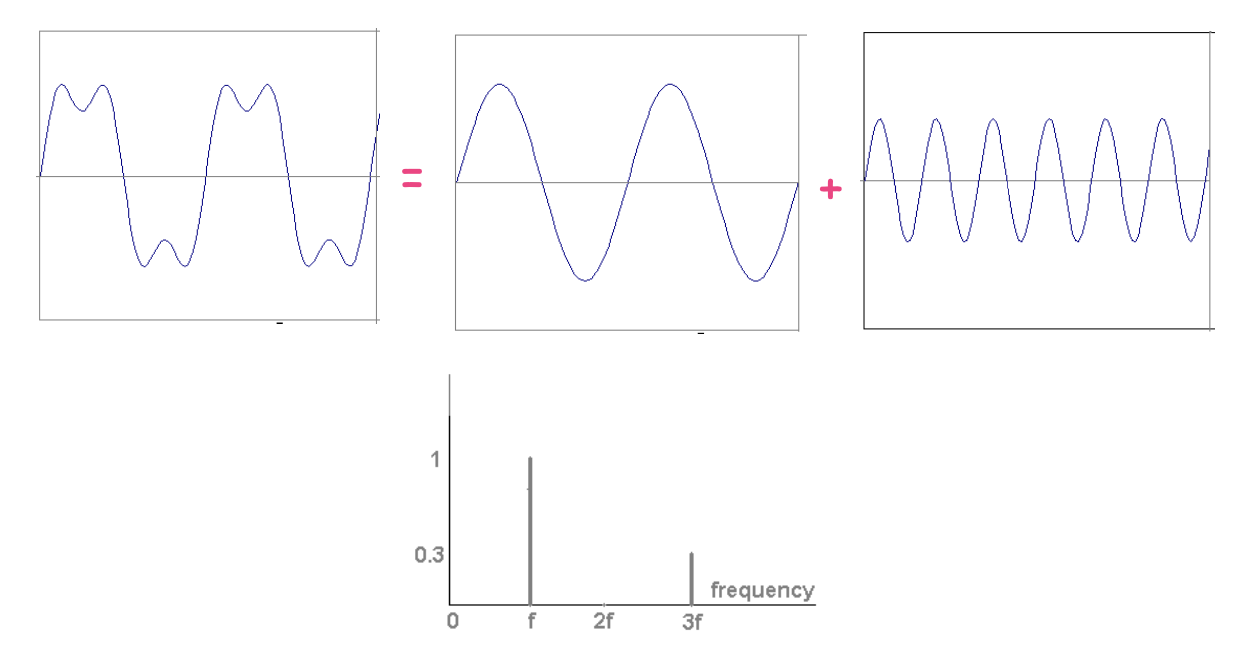위의 식에서 $p$는 $\pi$를 의미하고 $t$는 phase가 되는데, $g(t)$의 Fourier transform을 계산하게 되면 $F(\omega)$를 얻게 된다. 그리고 $\omega$의 값에 따라 서로 다른 amplitude와 phase의 값을 얻게 된다. 이번에는 다른 예시를 보도록 하자.

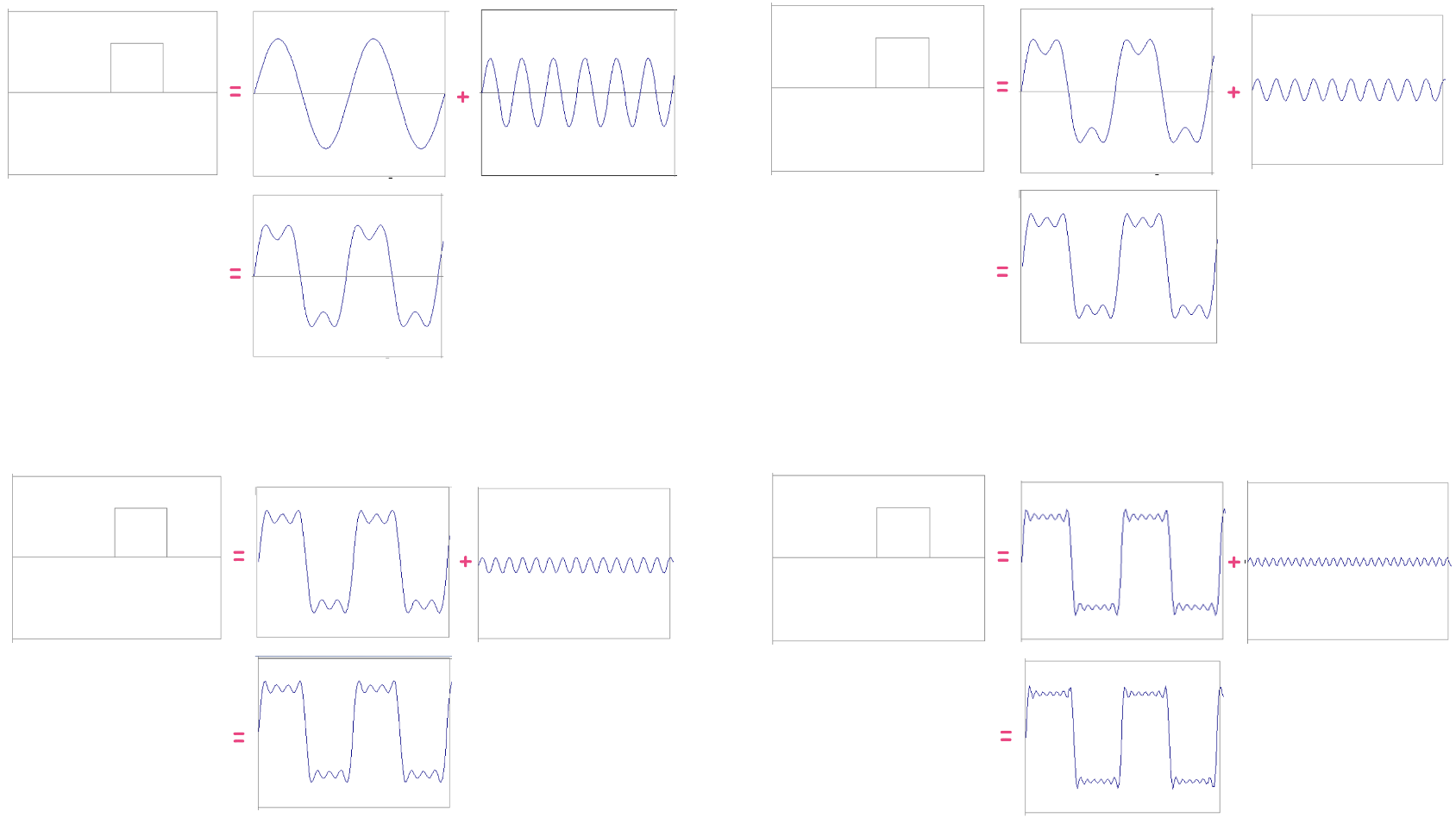위와 같은 주기 함수를 sin 함수의 합으로 표현을 할 때, higher frequency component를 계속해서 더해주게 되면 더 나은 approximation을 얻어 낼 수 있다. 그리고 이를 무한하게 하다보면 완벽한 결과에 도달하게 될 것이다.

그리고 이렇게 원래의 function의 Fourier transform을 이용하게 되면 다음과 같이 표현할 수 있다.
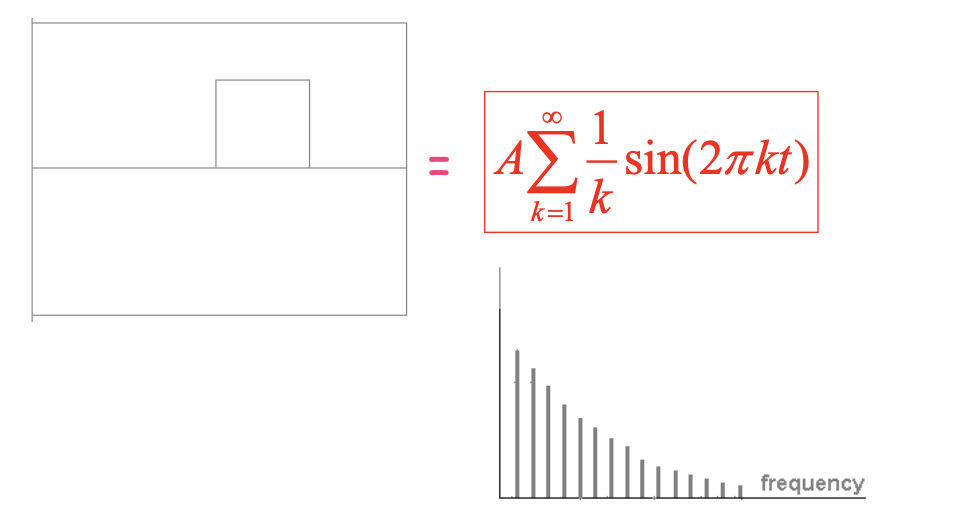이러한 결과는 각기 다른 frequency component에 따른 magnitude를 위와 같이 시각화 할 수 있다. 이를 frequency spectra라 하며, low frequency 일수록 large magnitude를 보이고, high frequency 일수록 low magnitude를 보이게 된다.

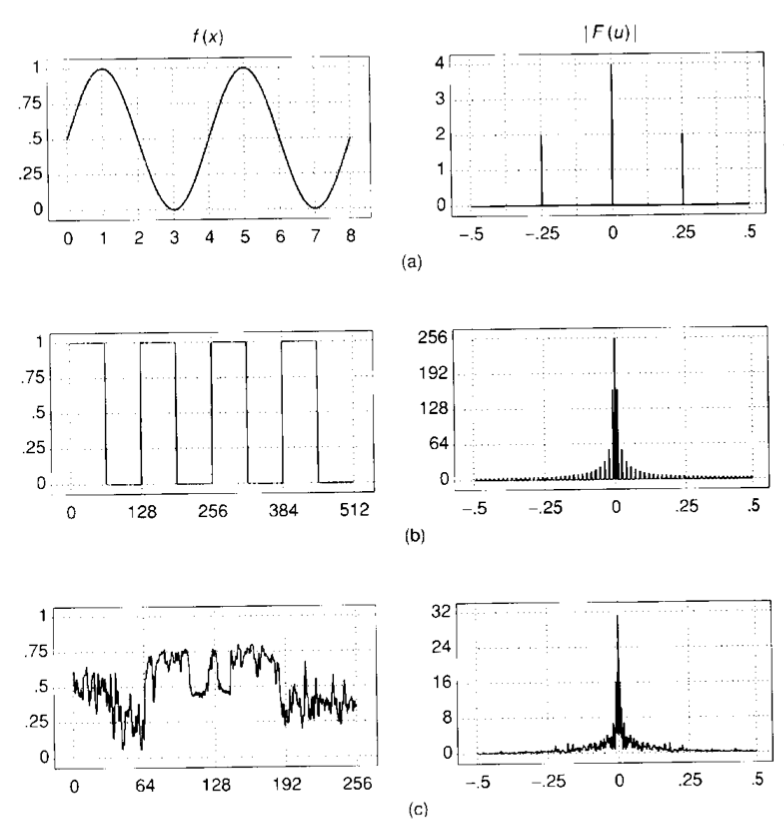이 외에도 또 다른 예시들을 볼 수가 있다. 좌측은 원래 signal들이고, 이들의 frequency spectra는 우측에서 확인할 수 있다. (a)는 3개의 non-zero 값을 가지는 것을 볼 수 있고, 나머지는 위에서의 plot과 비슷한 경향을 보이고 있다. 특히, (c)는 signal이 불규칙적인 경향을 보이고 있지만, frequency spectra는 비슷한 것을 볼 수 있다. 모두 비슷한 특징으로는 낮은 fruqency 일 때, 가장 큰 magnitude를 가지고 있다는 것이다.

Digital 이미지를 다룰 때, 2D digital 이미지는 continuous 하지 않다. 이들은 discrete function이고, parameter들도 discrete한 값들이다. 그래서 이미지의 경우 function으로 정의하기 위해서는 x, y가 discrete 해야 한다. 그래서 0, 1, 2, ... 와 같이 정의가 된다. 그래서 function value는 특정 위치의 intensity 값이 된다. 그래서 digital 이미지를 다루기 위해서는 Fourier transform 식을 수정할 필요가 있다.

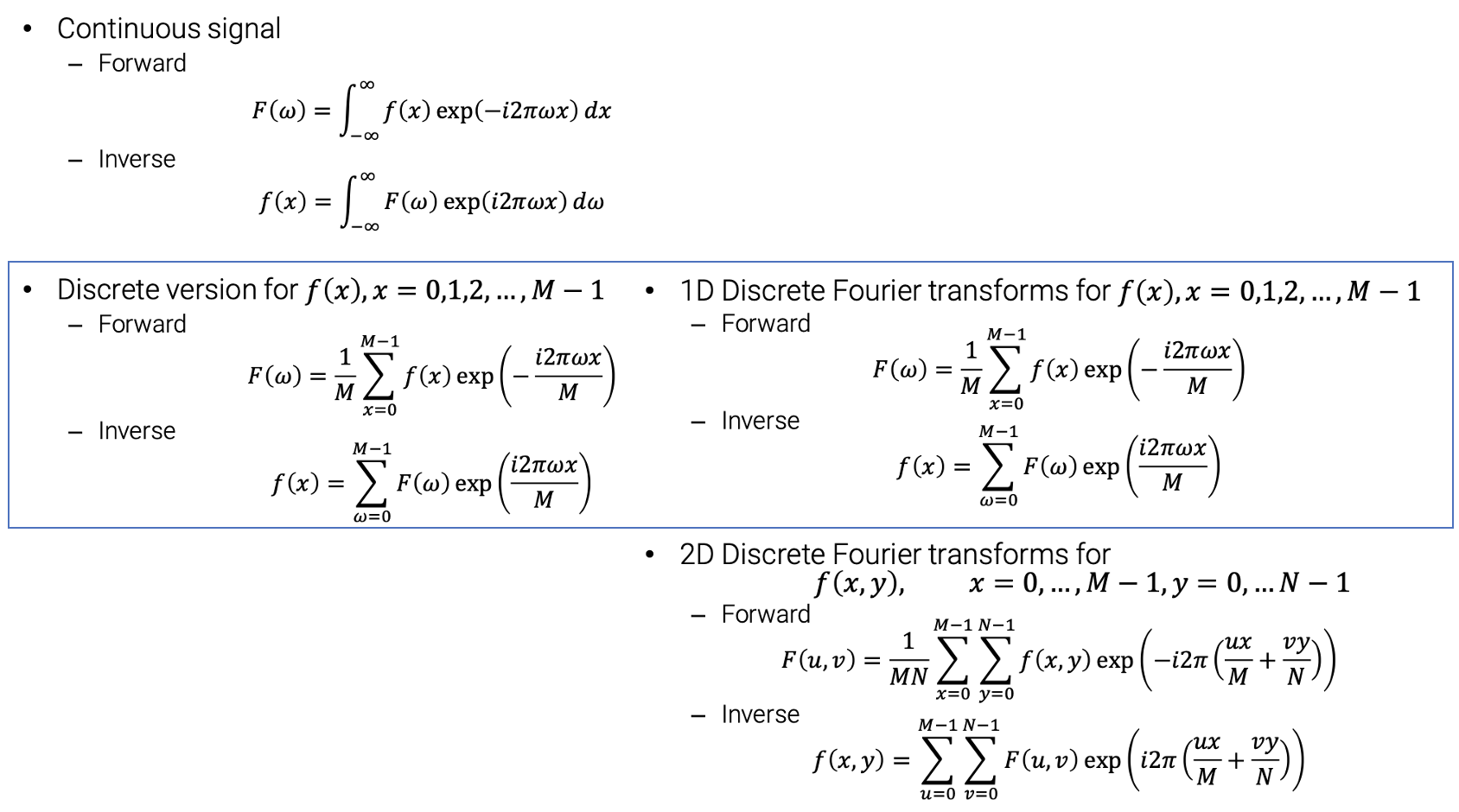Continuous Fourier transform에서 discrete Fourier transform으로 바꿀 때 형태가 integral에서 summation이 되는 것을 볼 수 있고, 이를 다시 2D digital image에서 사용하기 위해서는 summation이 하나가 더 추가가 된다.

1D continuous Fourier transform에서는 input signal을 magnitude, frequency, phase가 다른 sin function으로 분해할 수 있다. 그렇다면 2D Fourier transform은 어떨까? Input 2D signal을 다른 2D sin function으로 분해할 수 있다. 그리고 이 2D sin function들은 마찬가지로 다른 magnitude, frequency, phase를 가지게 된다.
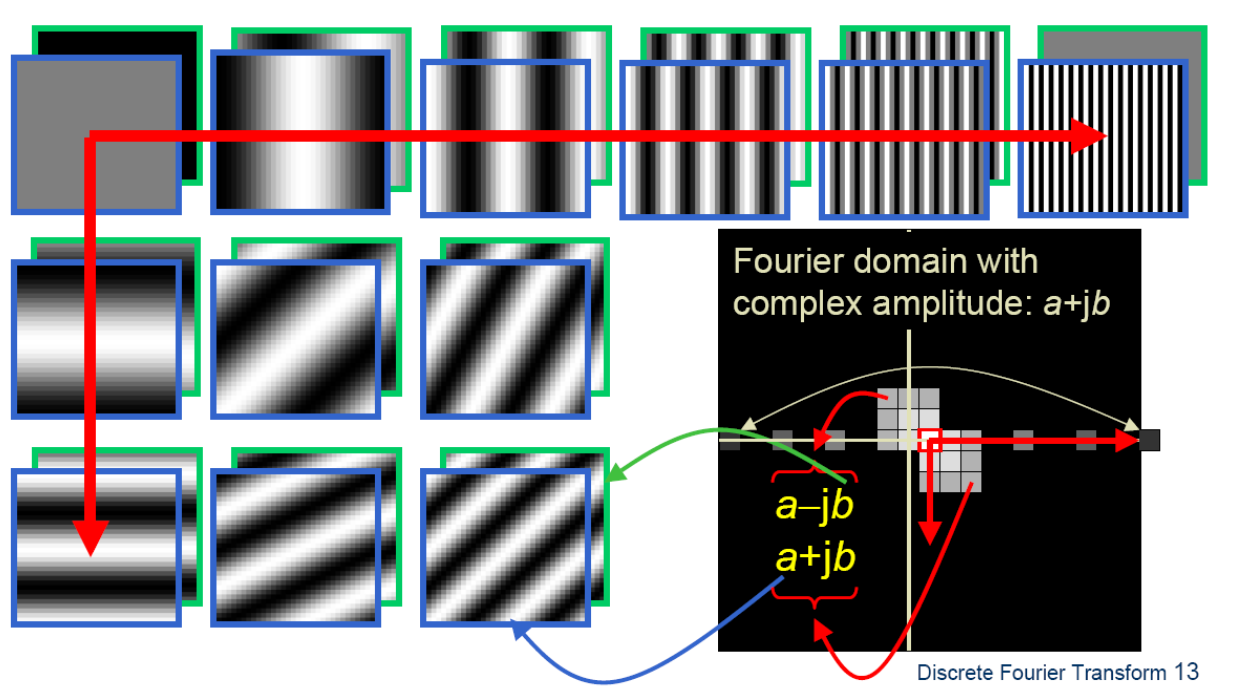파란색과 초록색 2가지로 나타나는 이유는 2차원에서는 complex number로 표현이 되기 때문에 real number 부분과 imaginary number 부분이 있기 때문이다. 그리고 $u$ 방향과 $v$ 방향으로 표현이 되며, 이 값들은 각각의 축을 따라서 frequency로 결정이 된다. 그리고 이 값들이 0인 경우에는 DC component라고 부른다.

좌측의 이미지를 log transform을 취한 Fourier transform의 결과가 우측의 이미지이다. 우측의 이미지는 좌측 이미지의 gray scale 버전의 frequency spectra인데 여기에 log를 취한 결과이다. 이미지 중간 지점을 lowest frequency component 혹은 DC componenet라고 하며, 이 지점은 이미지의 평균이나 전체 intensity를 나타내게 된다.
그렇다면 Fourier transform의 결과에서 나타나는 하얀 선같은 존재는 무엇일까? 좌측 이미지를 다시 살펴보자. 좌측에서 상단을 보면 우상단으로 큰 edge가 보일 것이다. 바로 이 지점 때문에 나타난 결과로 우측의 흰색 선은 원래의 지점과 sin function에 대응해서 생기게 된다. 그리고 흰색 선의 방향이 다른 이유는 주어진 이미지의 edge와 orthogonal한 방향으로 형성되기 때문이다. 이 또한 Fourier transform의 수식과 연관성이 있다. 그리고 우측 이미지에서 외곽으로 갈수록 frequency는 커지게 된다.