[계산사진학] Global Optimization 2

JAEYOON SIM·2021년 11월 22일

Computational Photography

목록 보기

26/34

Another Example: Image Denoising

이전에 살펴본 regularization optimization을 어떻게 활용할 수 있을까? Image denoising을 예시로 좀 더 실용적으로 살펴보도록 하자. Image denoising의 목표는 input noise image $g$ 가 있을 때, 이와 비슷한 image $f$ 를 찾는 것이다. 여기서 image $f$ 는 매우 작은 gradient를 가지고 있어야 하는데, 이는 noise가 적어야 한다는 의미이다. Noise image가 있고 중간에 가상의 line을 그렸을 때, line에 해당하는 pixel들의 intensity 값을 자세히 보면 굉장히 진동하는 형태로 존재할 것이다. 그래서 이 상태로 gradient를 구하면 그 값은 매우 클 것이다. 그래서 noise가 많으면 gradient는 상대적으로 커지게 된다. 반면, noise가 없는 image는 가상의 line을 그렸을 때 intensity 값들이 진동하지 않고 smooth한 선으로 나타날 것이다. 이는 gradient를 계산하면 그 값은 매우 작게 나타날 것이다. 그래서 energy function을 다음과 같이 수식화 할 수 있다.

Ɛ(f)=\sum_{x,y}|f(x,y)-g(x,y)|^2+\lambda\sum_{x,y}\|\nabla f(x,y)\|^2

Resulting image $f$ 가 input image $g$ 와 비슷해야 한다는 것이 앞쪽의 항이고, $f$ 의 gradient 값이 작아서 0에 가까워야 한다는 것이 뒤쪽의 항이다. 이 energy function은 이전에 이미 다루었던 내용이다. 그래서 이 energy function을 최소로 만드는 해를 찾음으로써 image denoising을 수행하는 것이다. 그러면 시각화한 결과를 보도록 하자.

좌측은 noise input image이고, 우측은 energy function을 최소로 하는 해를 찾은 것이다. Noise를 상대적으로 많이 없앤 것 같지만 또 다른 문제가 존재한다. Input image에서는 edge가 선명하게 보이지만, result image에서는 edge마저 선명함이 사라졌다. 그래서 비록 noise가 많이 사라졌다고 하더라도 부자연스러운 결과를 초래한 것이다. 이러한 문제가 발생한 이유는 energy function의 두번째 항 때문이다. 우리는 모든 pixel에서 gradient가 작은 image를 원한다. 그런데 사실 선명한 edge일수록 gradient 값이 커지게 된다. 왜냐하면 edge는 진한 검정색이고 그 주위는 밝은색이기 때문이다. Noise만 제거하고 edge는 보존해야하지만, smoothness term은 gradient만을 보기 때문에 이러한 edge마저도 gradient가 0으로 수렴하게 되어버린 것이다. 그 결과 smooth한 blurry image를 얻게 된 것이다. 이 문제를 해결하기 위해서 energy function의 smoothness term을 수정할 필요가 있고, 그래서 noise를 측정하는 방식을 살짝 바꿔줘야 한다.

그래서 이번에는 좀 다른 예시를 보고자 한다.

e(f) = \sum_{x,y}|f(x,y)-g(x,y)|^2+\lambdaƐ_{TV}(f)

Ɛ_{TV}(f)=\sum_{x,y}\{|f(x+1,y)-f(x,y)|+|f(x,y+1)-f(x,y)|\}

Data term은 여전히 같지만 smoothness term에는 다른 function을 사용했다. 기존의 smoothness term과 유사하게 보이는데 자세히보면 기존에는 L2-norm을 사용했지만 이번에는 L1-norm을 사용했다. Image gradient의 L1-norm을 total variation이라 부른다. Total variation은 digital image processing에 자주 사용되어지고 있다. 비록 total variation이 L2-norm 기반의 smoothness term과 비슷할지라도 이를 최소화함으로써 다음과 같이 선명한 image를 얻을 수 있다.
왜 total variation term을 최소화함으로써 선명한 image를 얻는 것일까? 왜냐하면 사실 이는 lasso regression과 밀접한 관련이 있다. 반면 L2-norm 기반의 smoothness term은 ridge regression과 관련이 있다. Lasso regression은 sparse solution을 선호한다. 자세한 내용은 넘어가지만 이렇게 total variation을 최소로 만들면 선명한 결과를 얻을 수 있게 된다.

그러면 이제 total variation term을 optimization 하는 방법에 대해서 알아볼 것이고 자세한 디테일은 다음과 같다.

Bayesian Approach

첫번째로 regularization approach와 variational approach를 알아보았고, 두번째로는 Bayesian approach에 대해서 알아볼 것이다. Bayesian approach는 variational approach와 밀접한 관련이 있지만, 여기서는 문제를 modeling할 때 probability distribution을 사용한다. 다시 image denoising을 예시로 들어서 먼저 noise image formation process를 다음과 같이 modeling 했었다.

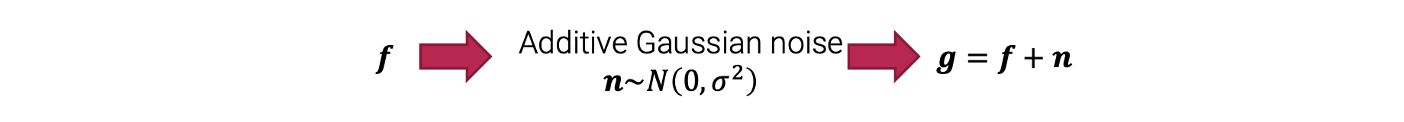먼저 noise가 없는 깨끗한 image $f$ 를 준비한다. 그러면 이 $f$ 는 additive Gaussian noise에 의해서 바뀌게 된다. 이때 noise는 Gaussian distribution을 따른다. 그러면 noise image $g$ 가 생기고, 원래의 image $f$ 에 noise $n$ 을 더한 형태가 된다. 이 과정이 일반적으로 noise가 생기는 과정이다.

이제 Bayesian approach에서 우리는 먼저 이러한 observed data generation process를 통한 model이 필요하다. 그러면 우리는 이 과정을 뒤짚고 싶다. 그래서 $g$ 로부터 깨끗한 image $f$ 를 찾을 수 있다. 이것이 우리의 목표이다. 그러나 이 문제 역시 noise로 인해서 놓치는 정보가 존재하기 때문에 ill-posed problem이고, 무한히 많은 해가 존재하게 된다. 이러한 이유 떄문에 추가적인 regularization이 필요하다. Bayesian approach에서는 문제를 regularization 하기 위해서 solution space의 statistical prior model을 가정할 것이다. 그래서 우리는 $f$ 의 probability distribution을 가정한다.

f \sim p(f)

여기서 $f$ 는 clean image, $p$ 는 prior distribution을 나타낸다. 이 경우에 prior는 우리에게 주어진 image가 얼마나 가능성이 있는지 말해준다. 예를 들어서 우리는 degradation이 없는 깨끗하고 자연스러운 image에 대한 prior를 필요로한다. 2개의 image가 있다고 가정해보자. 하나는 noisy image $f_1$ 이고 다른 하나는 clean image $f_2$ 이다. 만약 우리가 적절하게 distribution을 정의했다면 $f_2$ 의 probability가 $f_1$ 의 probability보다 반드시 커야만 한다. 그래서 이를 기반으로 해를 찾을 수 있다.

Advantages over Regularization

자세하게 더 들어가기 전에 Bayesian approach이 regularization approach보다 무엇이 더 좋은지에 대해서 알아보려고 한다.

Measurement process를 통계적으로 modeling하는 능력은 data를 제공할 가중치를 추측하는 것뿐만 아니라 각 측정에서 가능한 최대 정보를 추출할 수 있게 한다.
마찬가지로, prior distribution의 parameter는 종종 우리가 modeling하는 클래스의 sample들을 관찰함으로써 학습될 수 있다.
복구 중인 미지의 distribution에 대한 complete probability distribution을 추정하는 것이 가능하다.
Solution의 uncertainty를 modeling 할 수 있다.
Markov random field model은 regularization이 적용되지 않는 image label과 같은 discrete variable에 대해 정의할 수 있다.

우리는 어떻게든 data term과 regularization term을 정의했지만, 어떻게 이 term들을 정의하는지에 대한 실질적인 가이드라인은 없었다. 우리는 경험과 직관을 이용해서 정의했어야 했다. 그래서 기본적으로 적절히 수학적으로 정의하는 것은 어려운 부분이었다. 그러나 Bayesian approach에서는 실질적으로 어떻게 문제에 대해서 modeling을 하는지에 대한 가이드라인이 존재한다. 해를 구하기 위한 식은 수학적으로 타당해야하며 확률 기반으로도 타당해야 한다. 그래서 Bayesian approach는 어떻게 문제를 modeling을 하는지에 대해서 구체적으로 가이드 라인을 제시해줄 수 있다. 여기서는 여러 확률 기반의 도구들을 사용할 수 있다. 이러한 부분이 Bayesian approach의 장점이 된다.

예를 들어서 Bayesian approach에 대해서 설명해보도록 하자. 다시 image denoising을 예시로 들 것이다. $f$ 를 우리가 찾고 싶은 unknown이라 하고 noise가 없는 image라 하자. $g$ 는 observation으로 noisy image라고 할 것이다. 그러면 image denoising은 $g$ 가 주어졌을 때 가장 확률이 높은 $f$ 를 찾는 문제로서 수식화 될 수 있다.

f^\ast = \operatorname*{arg\,max}_f p(f|g)

Bayes' Rule

이는 그럴듯해보이나 문제가 존재한다. $p(f|g)$ 는 바로 modeling을 하는데 어려움이 존재한다. 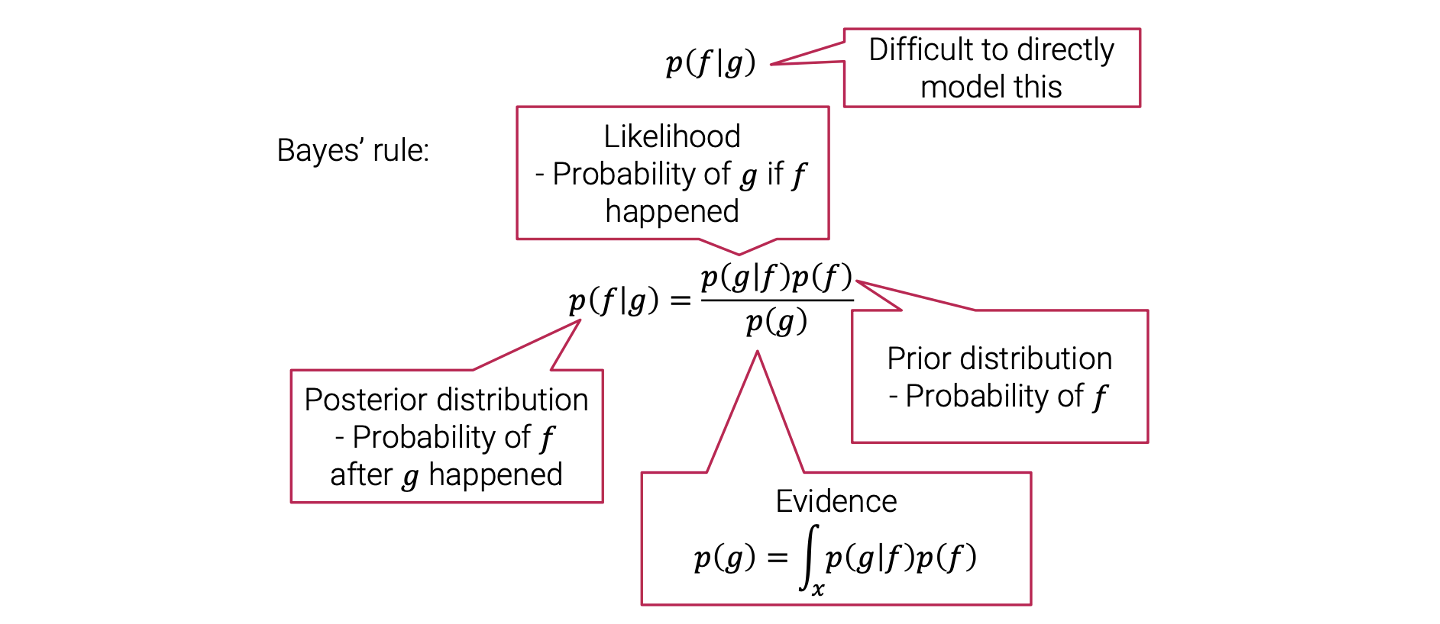그래서 이 식을 바로 사용하기 보다는 Bayes' rule을 적용해서 식을 변형할 것이다. Bayes' rule에서 $p(f|g)$ 는 posterior distribution으로 $g$ 가 일어난 후에 $f$ 가 일어날 확률이다. $p(g|f)$ 는 likelihoodfh $f$ 가 일어난 후에 $g$ 가 일어날 확률이다. $p(f)$ 는 prior dsitribtuion으로 $f$ 자체의 확률을 나타낸다. $p(g)$ 는 evidence이다.

왜 이러한 Bayes' rule을 사용해야 할까? 일반적으로 likelihood와 prior를 modeling 하는 것은 쉽다. 비록 posterior을 이용해서 modeling 하는 것이 어려울지라도 likelihood와 prior를 함께 modeling하는 것은 대부분의 경우에서 쉽다는 것이다. 그래서 Bayes' rule을 사용해서 식을 바꾸는 것이고 $g$ 는 $f$ 에 대해서 constant라서 다음과 같이 2개의 항으로 비례 관계만 따져도 상관이 없다.

p(f|g) \propto p(g|f)p(f)

Posterior distribution을 최대로 하는 $f$ 를 찾기 위해서 $p(g|f)p(f)$ 을 최대로 하는 해를 찾으면 된다. Bayes' rule에 따라서 likelihood와 prior를 modeling 할 필요가 있다. 다시 image denoising에서 다음과 같이 lieklihood와 prior를 modeling 할 수 있다.

$\text{Likelihood:}$

\text{We modeled: }g=f+n ,\,n\sim \mathcal{N}(0,\sigma^2)

\text{Therefore: }p(g|f)=\mathcal{N}(g-f|0,\sigma^2)

$g-f$ 는 $n$ 이 되고, 이 $n$ 는 normal distribution을 따르게 된다. 그래서 이 식은 가정으로부터 바로 도출된 것이다.

$\text{Prior:}$

p(f) = \frac{1}{Z}\text{exp}\bigg(-\frac{1}{\sigma_p^2}\sum_{x,y}\|\nabla f(x,y)\|^2\bigg)

Prior는 우리의 belief를 담고 있다.

MAP Estimation

우리는 likelihood와 prior를 정의했고, 이를 기반으로 다음 식을 풀 수 있다.

f^\ast = \operatorname*{arg\,max}_f p(f|g) = \operatorname*{arg\,max}_f \frac{p(g|f)p(f)}{p(g)}

Posterior distribution을 최대로 하는 것은 사실 negative log-posterior를 최소로 하는 것과 같다. 이렇게 식을 변형하는 것이 더 편리할 때가 많다.

f^\ast = \operatorname*{arg\,max}_f p(f|g) = \operatorname*{arg\,min}_f\{-\text{log }p(f|g)\}

$\text{Negative log posterior:}$

-\text{log }p(f|g)=-\text{log }p(g|f)-\text{log }p(f)-\text{log }p(g)=-\text{log }p(g|f)-\text{log }p(f)+C

그리고 여기서 likelihood는 normal distribution이기 때문에 다음과 같이 식을 정리할 수 있다.

-\text{log }p(g|f)=-\text{log }\mathcal{N}(f-g|0,\sigma^2)

=-\text{log }\frac{1}{Z}\text{exp}\bigg(-\frac{\|f-g\|^2}2{\sigma^2}\bigg)=-\text{log }Z+\frac{1}{\sigma^2}\|f-g\|^2

Prior도 다음과 같이 식을 정리할 수 있다.

-\text{log }p(f)=-\text{log }\frac{1}{Z}\text{exp}\bigg(-\frac{1}{\sigma_p^2}\sum_{x,y}\|\nabla f(x,y)\|^2\bigg)

-\text{log }Z+\frac{1}{\sigma_p^2}\sum_{x,y}\|\nabla f(x,y)\|^2

그래서 최종적으로 negative log posterior를 다음과 같이 다시 적을 수 있다.

-\text{log }p(f|g)=\frac{1}{\sigma^2}\|f-g\|^2 + \frac{1}{\sigma_p^2}\sum_{x,y}\|\nabla f(x,y)\|^2 + C

이 식은 매우 친근한 형태이다. Posterior distribution을 최대로 하는 것은 negative log posterior를 최소로 하는 것과 같고, 이로부터 constant는 상쇄하고 다음과 같이 새로운 식을 유도할 수 있다.

그래서 결론적으로 이 energy function을 최소로 만드는 문제를 풀면 된다. Bayesian approach를 사용하면 variational approach에서의 energy function을 유도할 수 있다. 그래서 Bayesian approach는 variational approach에서의 energy function을 찾는 방법에 대해서 가이드라인을 제시해준다. 이것이 Bayesian approach에 대한 주된 아이디어이다. 그리고 이 방식은 computer vision이나 graphics의 많은 곳에 사용이 된다.

JAEYOON SIM

평범한 공대생의 일상 (글을 잘 못 쓰는 사람이라 열심히 쓰려고 노력 중입니다^^)