[계산사진학] Global Optimization 1

Global Optimization

Image processing에서 optimization 기반의 approach에 대해서 알아볼 것이다. 먼저 numerical optimization problem에 대해서 다뤄볼 것이다. 이 문제는 구체적인 objective function을 풀어서 $x$라는 해를 찾아야 한다. $x$는 이 function $f(x)$를 최소로 만드는 해이다.

이 식에 추가적인 constraint도 존재할 수 있다. 예를 들어 다음과 같은 constraint가 있을 수 있다.

만약 이러한 constraint이 존재한다면 constraint optimization problem이라고 부른다. 그러나 보통 constraint optimization problem은 unconstraint optimization problem보다 해를 구하는게 다소 어렵다.

지금까지 여러 image processing 기법들에 대해서 알아보았고 대부분 다음과 같은 과정이었다.
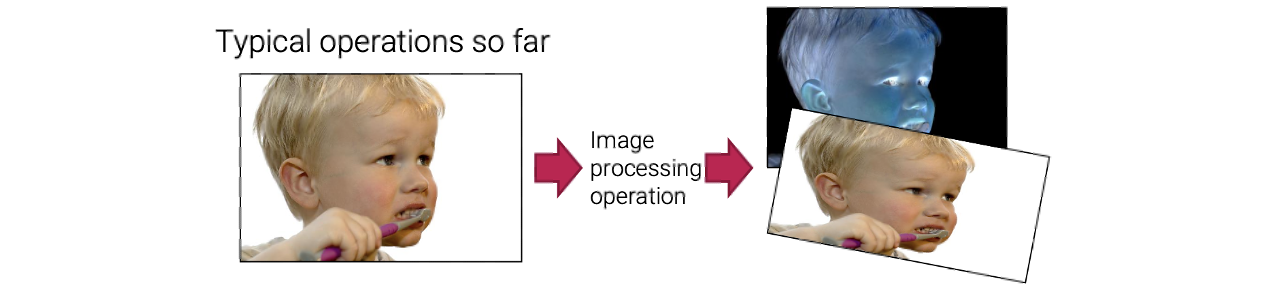좌측과 같이 input image가 주어졌을 때, image processing operation을 통해서 바뀐 결과를 얻게된다. 지금까지 배운 내용은 filtering이나 warping을 통해서 image를 변형시키는 것이었다. 그러나 많은 분야에서 먼저 optimization 기준을 사용하여 원하는 transformation의 목표를 공식화한 다음 이 기준을 가장 잘 충족하는 해를 찾거나 추론하는 것이 더 유용하다.

간단한 예시를 보도록 하자. 우리가 image denoising을 하고싶다고 해보자. Noise image $g$가 주어졌을 때 우리는 $g$처럼 보이지만 noise가 심하지 않은 새로운 image $f$를 찾고싶다. 이 문제를 풀기 위해서 다음과 같이 식을 세울 수 있다. 먼저 noise image $g$를 가정하고 새로운 image $f$에 noise가 얼마나 심한지를 측정해주는 function $Ɛ(f)$를 정의할 것이다. 그러면 이제 image denoising을 optimization problem으로 정의하여 식을 만들 수 있다.

그래서 우리는 noise의 양을 최소로 하는 image $f$를 찾고 싶고, 동시에 $f$는 $g$에 근사해야 하면서 noise는 적거나 존재하지 않아야 한다.

Least-Squares Method

Global optimiation problem을 더 자세히 다루기 전에 간단하게 least-squares method에 대해서 다시 한 번 보고 갈 것이다. 다음과 같이 data point들이 분포하고 있다고 해보자. 여기서 우리는 이 data들을 가장 잘 설명하는 straight line을 찾고 싶다. Data point를 $(x_i,y_i)$라고 했을 때, straight line을 다음과 같이 나타낼 수 있다.

위의 식에서 $a,b$를 찾아야 한다. 그러면 위의 식을 이용해서 objective function을 다음과 같이 만들 수 있다.

우리는 data point와 objective function간 error를 최소로 만들고 싶고, 이를 통해서 해를 구하고 싶다. 그렇다면 이 식을 어떻게 풀 수 있을까? Objective function을 matrix form으로 바꾸면 더 간단하게 문제를 풀 수 있다. 먼저, 각 data point에 대해서 다음과 같이 식을 적을 수 있다.

이 정보를 이용해서 matrix form으로 바꾸게 되면 다음과 같다.

이렇게 matrix $A$와 vector $b$를 정의하게 되면 다음과 같이 새롭게 식을 나타낼 수 있다.

이 식이 quadratic function이기 때문에 이 식을 $x$에 관해서 미분할 수 있다. 그래서 미분한 값이 0이 되었을 때의 $x$가 위의 식을 최소로 만드는 해가 되고 다음과 같다.

여기서 $(A^TA)^{-1}A^T$는 pseudo inverse라고 한다.

Two Approaches

Computer vision과 computer graphics 분야에서 global optimization approach는 regularization과 Bayesian 방식이 존재한다. 이 2가지 접근법은 서로 밀접하게 연관되어 있다.

Regularization or Variational Approaches

Regularization approach는 regularization의 이론을 기반으로 하고 있다. Regularization approach는 solution space를 심각하게 제약하는 data에 모델을 맞추려는 통계학자들에 의해서 처음 등장하였다.

Toy Problem Example

먼저 toy example에 대해서 보도록 하자. 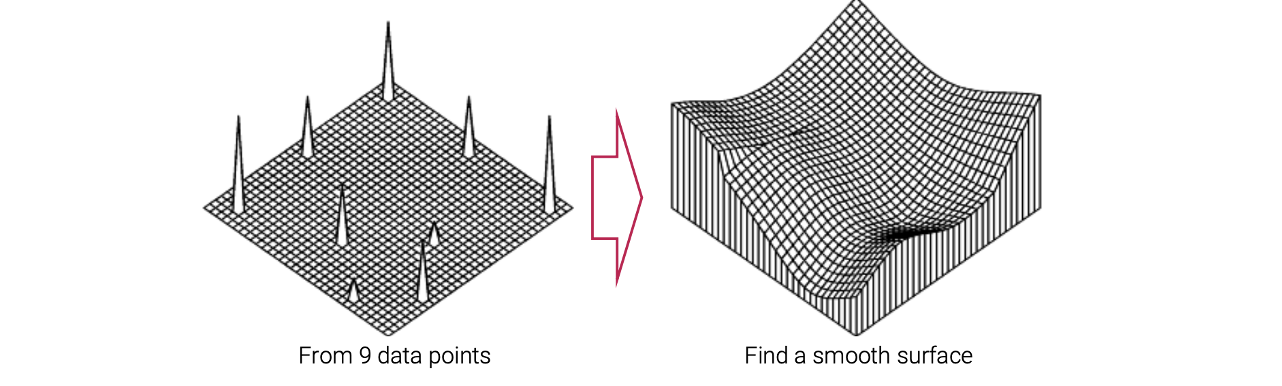Toy problem은 9개의 data point를 가지고 있다. 여기서 우리는 이 point들을 통과하는 smooth surface를 찾고 싶다. 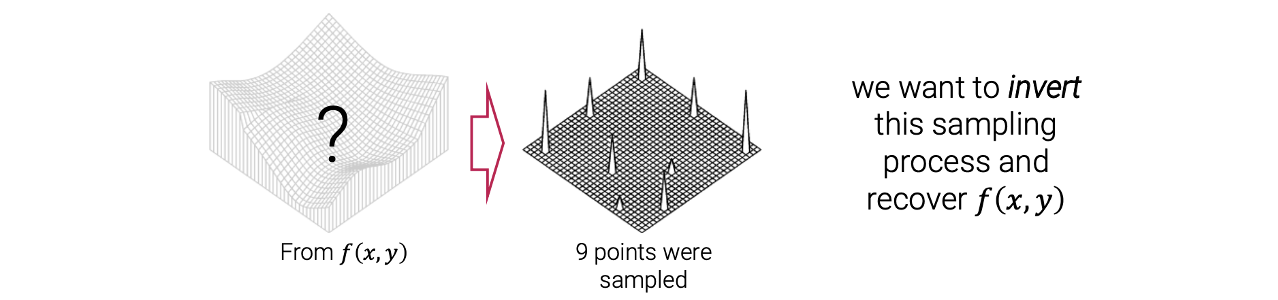이 문제는 inverse problem으로 간주될 수 있다. 반대로 우리는 smooth surface를 가지고 있다. 어떠한 observation process를 통해서 이 smooth surface로부터 우리는 9개의 point들을 sampling할 수 있다.

예를 들어서 smooth surface가 모르는 image라고 하자. 우리는 해당하는 9개의 point들에 대해서 pixel 값은 알고 있다. 이 image에서 9개의 지점에서 pixel 값은 알고 있고 추가적으로 이 image가 smooth하다는 정보도 알고 있다. 여기서 smooth하다는 것은 pixel 값이 부드럽게 바뀐다는 것이다. 여기서 이제 어떤 observation process를 통해서 오직 9개의 data point만 남게 될 것이다. 우리가 하고 싶은 것은 이 sampling process와 원래 image $f(x,y)$ 복구를 뒤짚고 싶은 것이다. 그래서 우리는 sampling process를 뒤짚어서 9개의 point로부터 시작해서 smooth surface로 가고 싶은 것이고, image $f(x,y)$를 복구하고 싶다. 이러한 과정을 inverse problem이라고 한다.

Inverse Problem

우리는 제한된 image 집합으로부터 3D 세계의 완전한 설명을 복구하려고 노력하기 때문에 많은 computer vision task들은 inverse problem으로 볼 수 있다. 좌측과 같이 3D 세계가 존재한다고 해보자. 그러면 이 세계에서 image를 캡쳐하게 되면 2D image를 얻게 된다. Computer vision에서는 이 과정을 뒤짚어서 3D 세계를 복구하기를 원한다. 즉, 2D image를 3D로 바꿔야 한다. 그래서 이 또한 inverse problem이 된다.

Ill-Posed

Inverse problem에서는 알아야 할 중요한 개념들이 몇가지 있다. 그 중 첫번째가 ill-posed, 혹은 ill-posedness이다. 예를 들어 위와 같이 4개의 point가 있다고 해보자. 우리는 이 4개의 point를 모두 통과하는 curve를 찾고 싶다. 이 문제의 해는 무수히 많이 존재한다. 그래서 ill-posed problem은 무수히 해가 많은 문제를 말한다. Computer vision과 image processing에서 inverse problem과 종종 ill-posed problem이다.

예를 들어 super-resolution은 저해상도 image를 가지고 고해상도 image를 찾아야 한다. 저해상도 image는 pixel 개수가 굉장히 적다. 그래서 downsampling을 해서 이 저해상도 image를 만드는 고해상도 image는 무수히 많이 존재한다. 그래서 super-resolution도 ill-posed proble이 되는 것이고, 또한 inverse problem으로 여겨질 수 있다. 왜냐하면 원래 고해상도 image를 가지고 있고 image degradation process 등을 통해서 저해상도 image를 얻게 된다. 그래서 우리는 저해상도 image를 만드는 과정을 뒤짚어서 고해상도 image를 복구하고 싶다. 그래서 super-resolution은 inverse problem이고 동시에 ill-posed problem이다.

Ill-Conditioned

또 다른 중요한 개념은 ill-conditioned이고, 이는 input의 작은 변화가 때때로 output의 큰 변화를 초래하는 경우를 말한다. 예를 들어 scaling factor $a$가 있다고 해보자.

그리고 미지수 $x$와 constant $b$가 있다. 이미 $a,b$는 알고있고 $x$를 찾고 싶다고 해보자. 여기서 $a$를 추정값이라고 해보자. 이는 어떠한 error가 존재할 수 있다는 것을 의미한다. 그리고 $a$의 크기는 작다. 또한 $b$도 추정값이라고 해보자. 그러면 $b$도 error를 가질 수 있게 된다. 그러면 이 예시에서 $b$의 작은 변화는 $a$가 0에 가깝기 때문에 $x$의 변화를 크게 만든다. $b$의 error가 $x$의 변화를 크게 만든 것이다. 그래서 이러한 문제를 ill-conditioned problem이라고 한다. 다음 예시도 보도록 하자.

이 식은 하나의 방정식이 아니라 linear system을 가지고 있다. 그리고 $x$를 위와 같은 방식으로 구할 수 있다. 만약 $A$가 non-invertible에 가까워질수록 이 문제도 또한 ill-conditioned problem이 될 수 있다. Non-invertible이란 inverse를 찾기 어렵다는 것이다. 우리는 $A$가 non-invertible에 얼마나 가까운지 condition number $\kappa(A)$를 계산함으로써 측정할 수 있다. 만약 $\kappa(A)$가 크면 $A$가 non-invertible에 가까워진다. 이러한 경우에 $b$의 작은 변화가 $x$의 변화를 크게 만든다. 그래서 이러한 문제도 ill-conditioned problem이라고 할 수 있다.

Regularization

Regularization 이론은 ill-posed, ill-conditioned problem을 풀기 위해서 등장했다. 그래서 간단한 예시를 볼 것이다.
여기 4개의 observed point들이 있다. 여기서 우리는 이 data point들을 통과하는 function $f(x)$을 찾기를 원한다. 즉, function 값이 $(x_i,y_i)$와 비슷하기를 원한다. 우리는 이 문제를 inverse problem으로 modeling할 수 있다. 먼저 underlying function을 다음과 같이 가정할 것이다.

여기에 data point $y_1,y_2,y_3,y_4$가 $f(x)$로부터 $x_1,x_2,x_3,x_4$에서 다음의 process를 따라서 sampling되었다고 가정할 것이다.

각 $y_i$는 위와 같은 식을 통해서 sampling 되었고, 이는 각 $x_i$에서 먼저 function 값을 구하고 모르는 noise를 더했다. 이러한 sampling process를 통해서 $y_i$를 얻을 수 있고, 우리는 이 과정을 뒤짚고 싶다. 우리는 observed data point 주변을 통과하는 function $f(x)$를 찾고 싶다. 즉, 다음의 식을 최소로 만드는 curve를 찾고 싶다.

$Ɛ(f)$는 function $f$의 function이다. 그래서 이를 functional이라 부를 수 있다. Functional은 function을 scalar로 mapping하는 function이다. 이 식의 해는 무수히 많이 존재한다. 오직 4개의 data point가 존재하고 5개의 미지수가 존재하기 때문이다. 모든 coefficient는 우리가 찾고 싶은 미지수이다. 그래서 이 문제는 ill-posed problem이 된다. Ill-posed problem을 풀기 위해서는 추가적으로 constraint를 필요로한다. 그래서 우리는 추가적인 식이 필요하다. 추가적으로 필요한 constraint를 우리는 regularization이라 부를 것이다.

Regularization을 추가하기 위해서 우리는 문제에 대해서 또 다른 가정이 필요하다. 우리가 이 문제에서 찾고 싶은 것은 curve다. 목표하는 curve는 smooth curve라고 가정할 수 있다. 이 가정을 기반으로 smoothness를 측정하는 식을 first-order derivative를 이용해서 정의할 수 있다.

First-order derivative의 크기를 구할 것인데, 만약 curve가 smooth하다면 이 식은 작아져야 한다. 반대로 curve가 매우 크다면 이 식은 매우 큰 값을 반환할 것이다. 우리는 smoothness를 측정할 수 있는 식을 정의했기에 문제를 다시 다음과 같이 정의할 수 있다.

원래 항과 smooth 항을 조합함으로써 이 문제는 이제 유일한 해를 구할 수 있어졌다. 이러한 식으로 유일한 해를 구하기 위해서 문제를 regularization 했다. $Ɛ_d(f)$는 data term, data fidelity term이라 하고, $Ɛ_s(f)$는 regularization term, prior라고 한다. 여기서 regularization term은 smoothness term으로 사용되었다. 그리고 $\lambda$는 2개의 항의 균형을 조절해주는 parameter이다. 만약 $\lambda$가 크면 curve는 smooth해지지만 data point들로부터 멀어지게 된다. 반대로 $\lambda$가 작으면 curve는 덜 smooth해지지만 data point들에 가까워지게 된다.

Variational Approach

이렇게 regularization 기반의 approach를 variational approach라고 한다. 왜냐하면 이는 calculus of variations(변분법)에 기반을 두고 이는 variation을 사용하는 수학적 분석의 한 영역이기 때문이다.

Smooth Surface(2D)

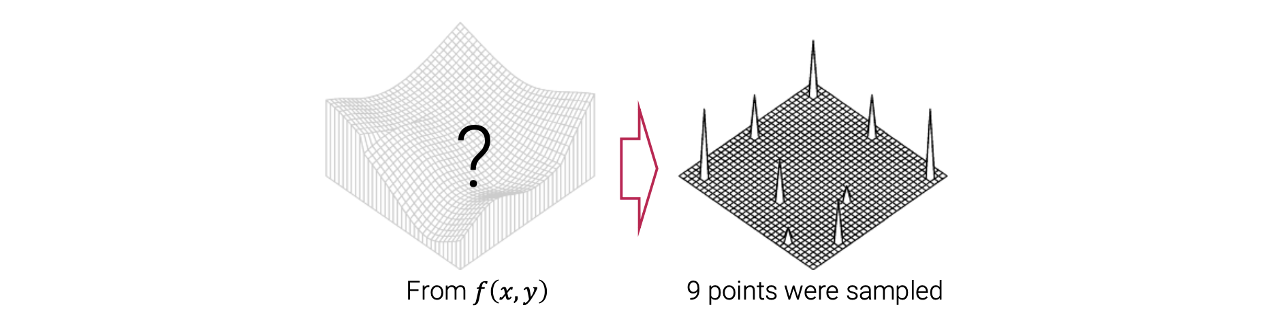이전의 toy example에서는 1차원의 data에 대해서 다뤄보았다. Computer vision이나 graphics에서는 digital image를 다루게 된다. Digital image는 2D data이기 때문에 확장해서 생각해봐야 한다.

우리는 알지 못하는 2D surface를 가지고 있다. 이로부터 9개의 data point를 sampling하고 싶다. 그러면 이 9개의 data point들로부터 처음에 알지 못하던 2D surface를 복구하기를 원한다. 우리가 하고싶은 것은 이 9개의 point를 통과하는 curve를 찾는 것이다. 그리고 smooth curve를 원한다. 만약 오직 9개의 data point만 가지고 있고 다른 가정이 없다면 ill-posed problem이 된다. 왜냐하면 9개의 data point만 가지고 있고 surface는 무작위로 될 수 있기 때문이다. 그래서 우리는 추가적인 constraint가 필요하고 이 constraint는 smoothness term이 될 것이다. 1차원 예시에서 정의했던 smoothness term을 확장함으로써 2차원에서의 smoothness term을 정의할 수 있다.

Discrete Version

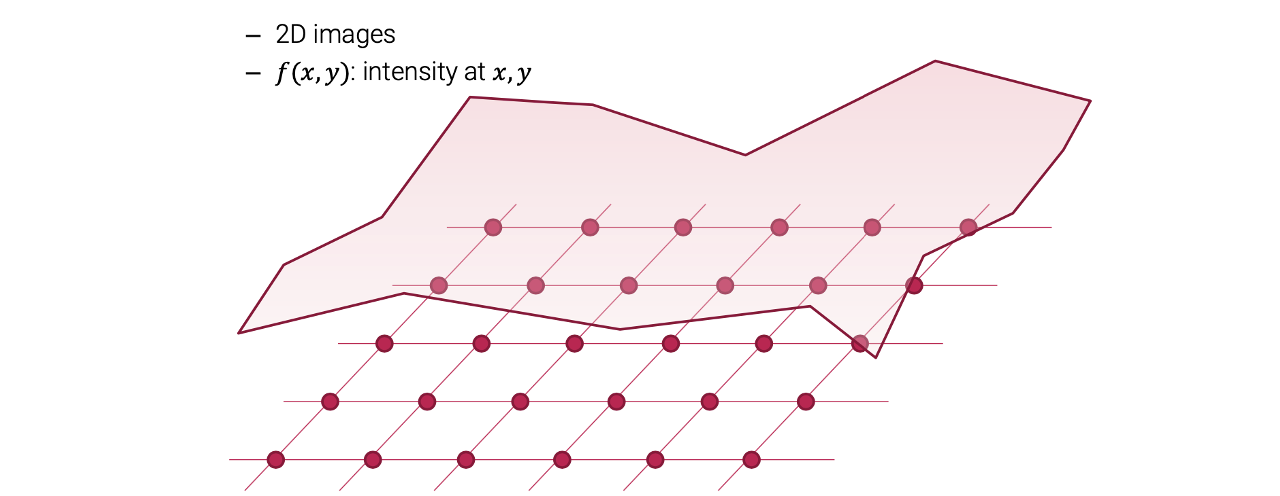Image processing에서 우리는 단순히 function이 아니라 digital image를 찾고 싶다. 1차원 예시에서는 $f(x)=ax^2+bx+c$와 같이 식을 정의했다. 그러나 digital image processing에서는 이러한 것은 불가능하다. 대신에 각 $x,y$에서 function 값이나 pixel 값을 가지는 2D function $f(x,y)=f_{xy}$를 정의하고 싶다.

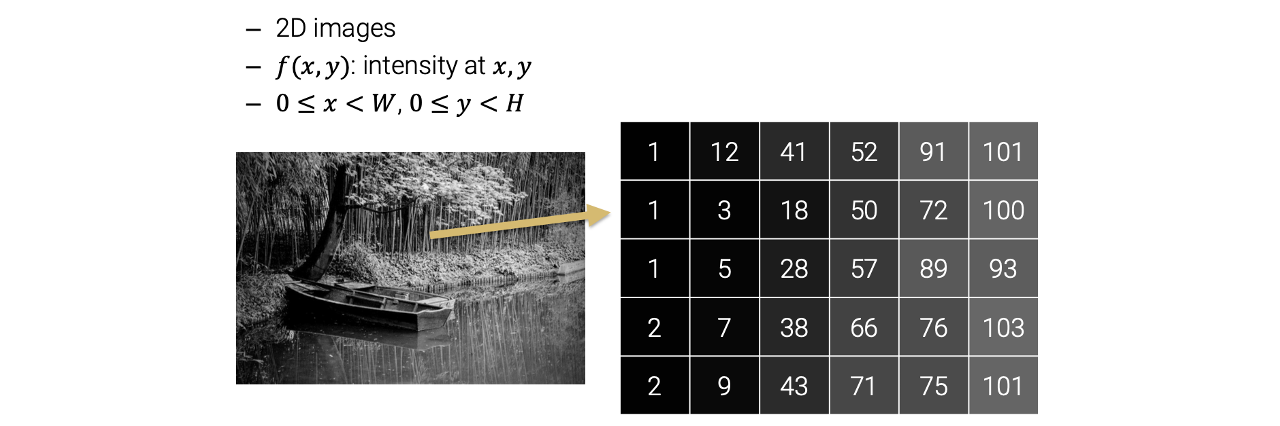우리는 2D function을 찾고 싶고, 이 2D function은 function 값이 pixel 값이 되는 digital image에 대응될 것이다. 그래서 이를 기반으로 1차원을 2차원의 discrete version으로 확장할 수 있다.

$\text{Smoothness(continuous):}$

$\text{Smoothness(discrete):}$

Smoothness term을 discrete version에 사용하기 위해서 finite difference method를 이용해서 위와 같이 변형할 수 있다. 기본적으로 derivative를 approximation할 수 있다. 그리고 data term도 다음과 같이 확장할 수 있다.

$\text{Data term(continuous):}$

$\text{Data term(discrete):}$

Data term은 똑같은 형태로 사용이 가능하다. 각 pixel 위치에서 pixel 값은 observed data point의 값과 비슷해야 한다. 그러면 실제로는 어떻게 modeling을 해야할까?

Linear System

Digital image나 function을 modeling을 해야한다. 그래서 image를 vector로 나타내기 위해서 energy function을 matrix form으로 바꾸는 것이 편리하다. 가령 digital image에서 좌측 상단의 pixel 값을 $f_{00}$라고 표기할 수 있다.

이렇게 모든 pixel 값을 1D vector로 모을 수 있다. 그러면 이제 smoothness term과 data term을 matrix form으로 다시 적을 수 있다.
$f$와 $D_x$가 dot product를 함으로써 difference를 계산할 수 있다. 그래서 $D_x$가 row마다 계산이 되도록 디자인되어 있다. $f$는 $HW$ 차원의 vector이다. 이는 이자체로 이미 매우 큰 vector이다. 그리고 $D_x$는 $HW\times HW$ 차원의 matrix이다. 만약 image의 크기가 $100\times 100$이라면 $D_x$는 $10000\times 10000$으로 매우 커지게 된다.

$D_x$의 또 다른 성질로는 diagonal entry 주변 일부를 제외하고 전부 0이다. 그래서 0의 개수가 정말로 많다. 이러한 matrix를 sparse matrix라 부른다. Sparse matrix가 중요한 이유는 $D_x$는 그 자체로 매우 커서 computationally inefficient하다. 그런데 만약 sparse matrix라면 사이즈가 크더라도 0인 값은 컴퓨터 상에 저장할 필요가 없어서 메모리를 많이 사용하지 않게된다. 그래서 이러한 요소가 속도적인 측면에서 빠르다. 즉, sparse matrix는 그 자체로 사이즈가 크더라도 비효율적이지 않다. 어쨋든 smoothness term을 위와 같이 나타낼 수 있고 data term도 다음과 같이 나타낼 수 있다.

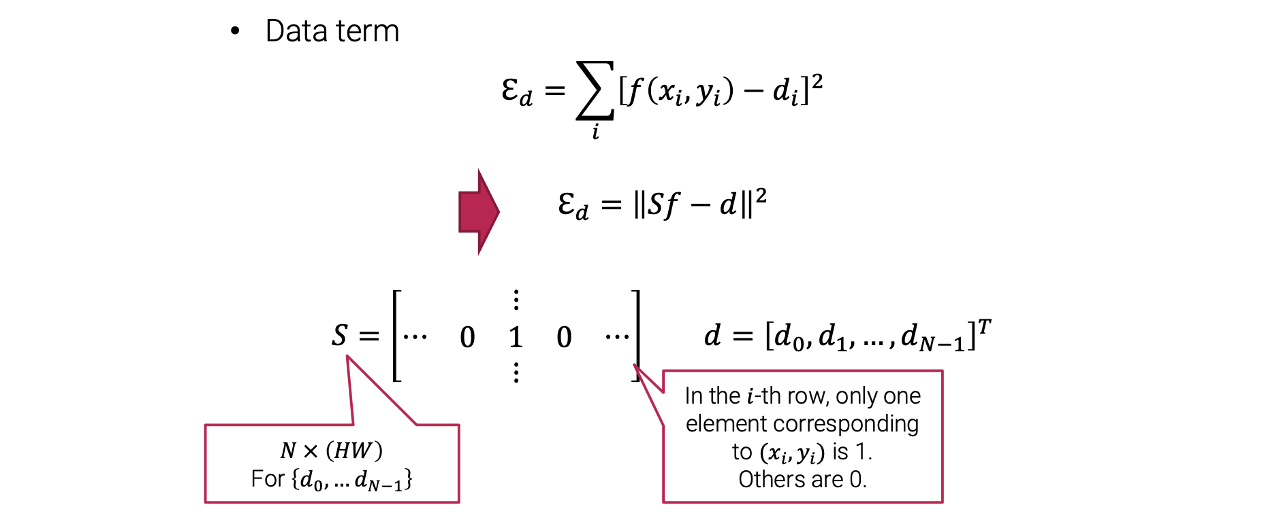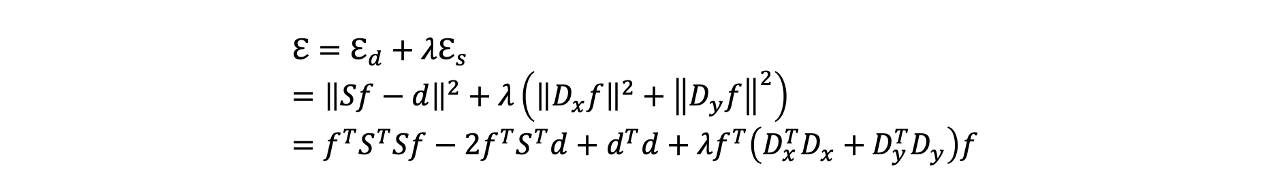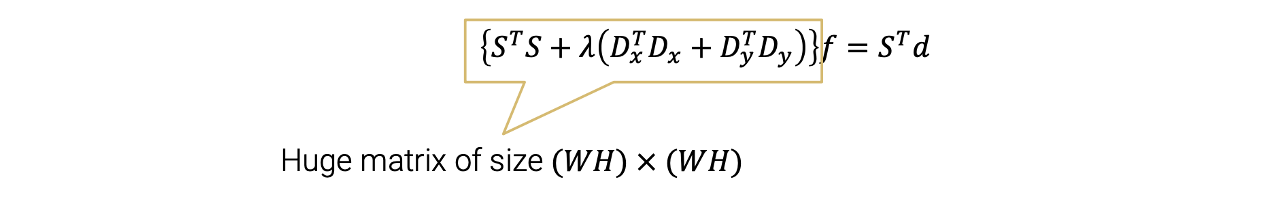우리는 기존의 data term을 matrix form으로 나타낼 수 있다. 그래서 이렇게 smoothness term과 data term을 조합해서 다음과 같이 quadratic function을 만들 수 있다. 우리는 이 function을 최소로 만드는 vector $f$를 찾고 싶다. 이 function이 quadratic function이기 때문에 vector $f$에 관해서 미분 할 수 있다. 이를 통해서 이 quadratic function을 최소로 만드는 global minimum을 찾으면 된다. 그래서 미분해서 0으로 두면 결과적으로 $Ax=b$와 같은 linear form이 된다. 이러한 sparse matrix로 된 linear system을 계산하는 library는 많이 존재한다. 예를 들어 Matlab에는 sparse()라는 함수가 있고 python에는 scipy.sparse라는 함수가 있다.