[계산사진학] Image Filtering - Linear Filtering

핸드폰으로 사진을 찍을 때 필터를 설정해서 사진을 찍은 경험이 있을 것이다. 이렇게 이미지에 특정한 필터를 덮어서 이미지의 분위기를 바꾸는 방법에 대해서 알아보려고 한다.

Spatial Filter

먼저, filter라는 것은 frequency domain processing으로부터 빌려온 이름이다. 그래서 frequency domain 상에서 filtering한다는 것은 이미지를 구성하는 특정한 frequency를 통과시키거나 변형시거나, 혹은 거부하는 것을 말한다. 이러한 과정을 통해서 우리는 이미지를 보정하는 것이다. 예를 들어서 lowpass filter는 모든 높은 frequency는 거절하고, 낮은 frequency만을 통과시키는 필터를 말한다. 그래서 spatial filtering은 공간 필터링을 말하며, 이는 이미지로부터 각각의 픽셀 값들을 해당 픽셀 값과 이웃한 픽셀 값들의 어떠한 함수에 의해서 이미지를 바꾸게 된다.

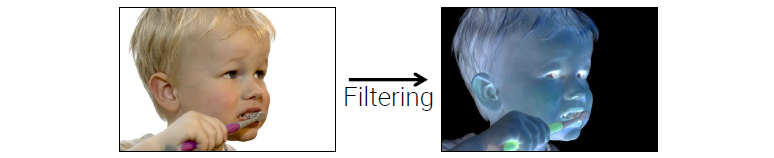
Frequencies in 1D Signal

1차원의 신호는 다른 frequency에 해당하는 component로 분해가 가능하다. 다음과 같이 어떤 신호가 들어왔을 때, 이를 low frequency와 high frequency의 합으로 표현이 가능한 것이다.

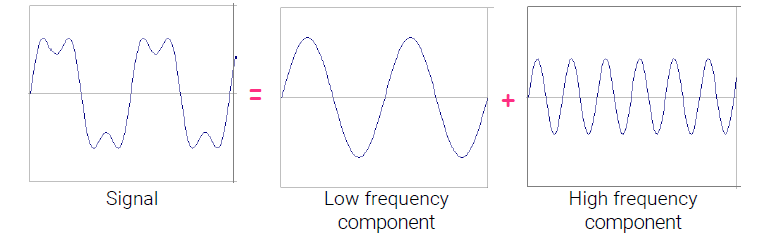
Frequencies in 2D Image

2차원의 이미지에서도 똑같이 분해가 가능하다. 이미지 위에 어떠한 가상의 선을 그어놓고 이 선을 따라 픽셀 값들을 시각화 했을 때, 우리는 위치에 따른 픽셀 값을 다음과 같이 얻을 수 있다. 이때, low frequency와 high frequency로 분해가 가능하며, low frequency들만 모아놓고 보면, 정보가 천천히 변하면서 부드럽게 그래프를 만들 수 있다. 이는 이미지를 smooth하게 만드는 효과를 가져온다. 반대로 high frequency만을 모아놓게 되면 정보가 굉장히 빠르게 변하는 것을 볼 수 있으며, high frequency 만의 정보를 얻을 수가 있다.

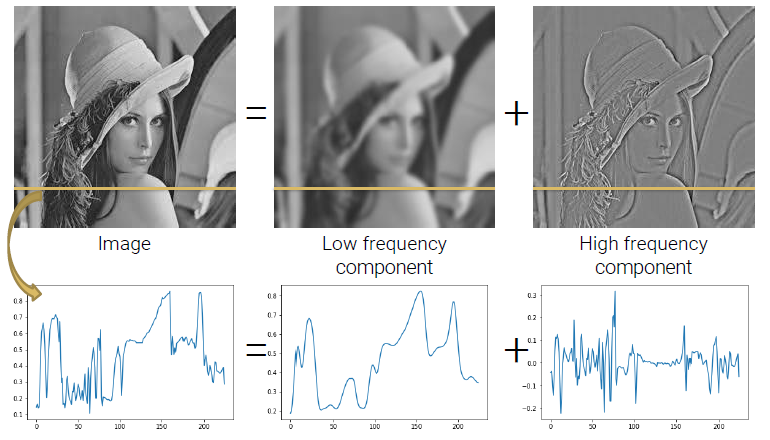
Linear Filter

Linear filter는 각각의 픽셀들을 해당하는 픽셀과 이웃한 픽셀들을 포함해서 linear combination을 이루어 값을 바꿀 수가 있다. 이때 linear combination은 filter의 kernel에 의해서 결정할 수 있으며, 이는 어떻게 만드는지에 따라서 이미지를 다양하게 바꿀 수가 있다. 모든 픽셀이 해당 픽셀과 이웃 픽셀의 동일한 linear combination을 사용하도록 동일한 kernel이 모든 픽셀 위치로 이동되게 된다. 다음의 예시를 보자.
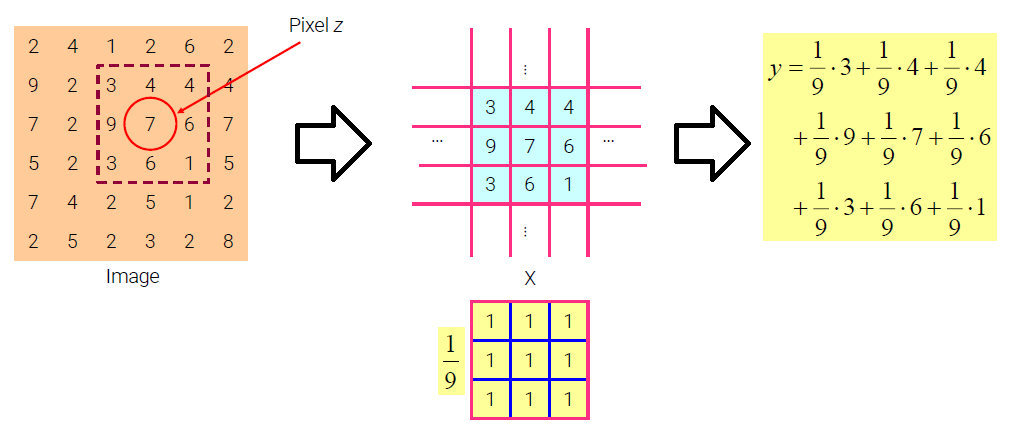$3\times3$의 어느 특정 부분으로부터 픽셀들의 평균을 어떻게 계산할 수 있는지 궁금한 것이다. 먼저 필요로 하는 특정 부분의 픽셀들을 선택하고, 모든 픽셀에 $\frac{1}{9}$을 곱해서 더할 것이다. 9개의 픽셀들을 사용하기 때문에 $\frac{1}{9}$을 곱해주는 것이다. 그러면 다음의 예시도 살펴보자. 이번에는 어떻게 모든 픽셀에서 $3\times3$의 평균 값을 구할 수 있는지이다.
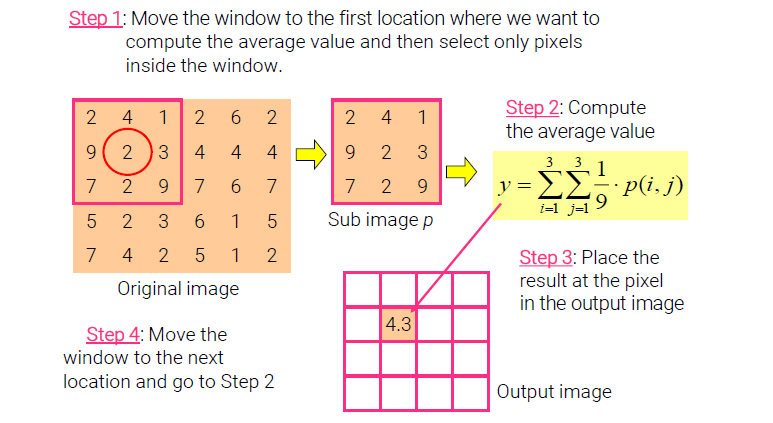방법은 위의 방법과 동일하며, 이를 확장하면 된다. 우선 가장 좌측 위의 9칸으로부터 평균 값을 구해서 이를 원래 가운데 값이 있던 픽셀 값을 대체하면 된다. 그리고 9칸을 한 칸 오른쪽으로 이동해서 다시 평균을 구하고 또 이동하여 평균을 구하는 식으로 진행하면 된다. 이때 이렇게 가운데 값을 평균 값으로 대체하게 되면 외곽의 테두리 부분의 값은 어떻게 채울 수 있을까? 그 내용은 뒤에서 살펴보도록 할 것이다.

방금 사용한 평균값을 구하는 filtering 같은 경우는 많은 linear filtering의 방법들 중에 하나일 뿐이다. Filter kernel의 크기를 바꿀 수도 있으며, 계산 방식을 다르게 할 수도 있는 것이다. 그래서 이제부터 여러 방법들에 대해서 살펴볼 것이다.

Convolution for 1D Continuous Signals

1차원 continuous 신호에 대해서 convolution filtering 식은 다음과 같다.

f는 filter, g는 input image, x는 pixel location을 의미하게 된다. 그래서 $(f * g)$는 이미지에 filtering을 한 결과를 나타낸다. 범위가 무한으로 표기가 되었지만, filter의 크기를 결정해주는 것에 따라서 범위는 특정한 범위로 조정이 된다.

다음은 box filter를 예시로 든 것이다. Box filter는 근본적으로 주변의 픽셀 값으로부터 평균을 얻는 이미지 filtering 방식으로, convolution filter 중 하나이다.

위의 filter를 이미지에 덮어주게 되면 다음과 같이 식이 결정이 된다.

Convolution for 2D Discrete Signals

2차원 discrete 신호에 대해서 convolution filtering 식은 다음과 같다.

2차원의 데이터에 대해서는 변수가 x, y로 이미지 상에서는 픽셀의 위치 정보가 될 것이고, 적분 기호였던 것이 시그마 기호로 바뀌게 되었다.
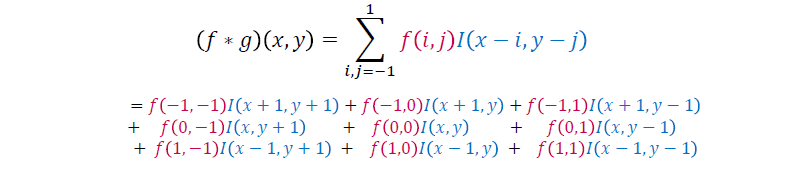Filter의 값이 0이 아니라면, 위와 같이 계산이 가능하다. $3\times3$ filter를 사용하면 9개의 항이 나오면서 덧셈 연산을 진행해주면 된다.

Convolution vs. Correlation

Convolution filter가 어떻게 이미지에 적용이 되고 계산이 되는지 알아보았다. Discrete한 2차원 convolution과 correlation을 비교해 볼 것인데, 이는 다음과 같이 수식에서 부호만 다르고 나머지는 같은 것을 확인할 수 있다.
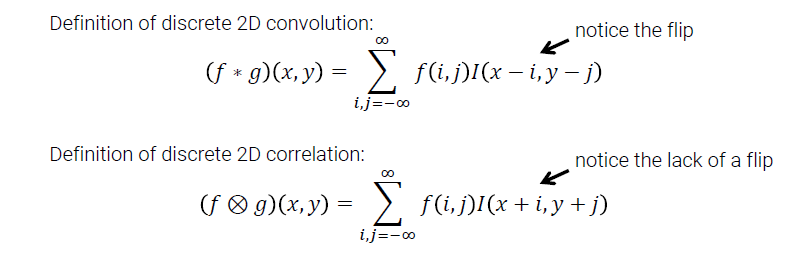식에서 알다시피 만약에 kernel이 symmetric하다면 convolution과 correlation의 결과는 같을 것이다. 하지만 non-symmetric하다면 convolution과 correlation은 전혀 다른 결과를 가져올 것이다. 우리는 correlation을 convolution으로 바꿀 수가 있는데, 이는 단순히 kernel을 수평 방향과 수직 방향으로 뒤집어주면 된다. 다음은 두 filter를 적용했을 때의 예시이다.
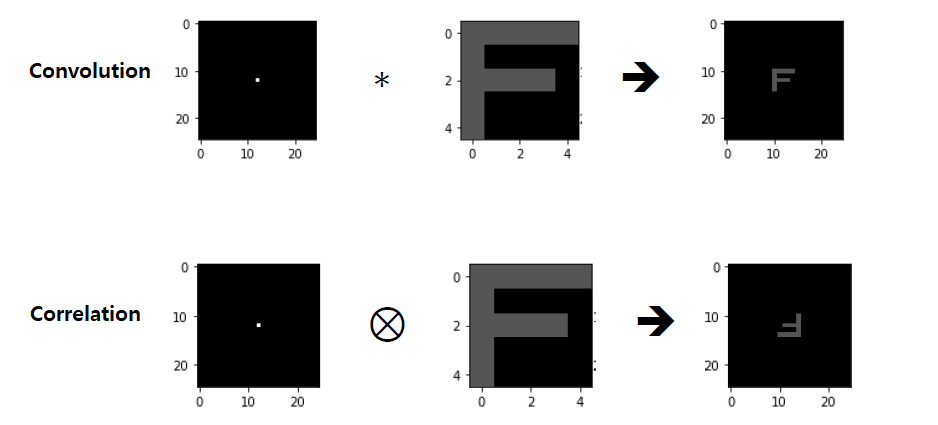Covolution과 correlation 모두 비슷한 결과를 내는 것을 볼 수 있지만, correlation의 경우 상하좌우로 뒤집히는 것을 볼 수 있다. 이는 부호의 차이로부터 발생한 결과로 해석할 수 있다.

Convolution과 correlation의 차이는 부호밖에 없지만, 사용하는 용도와 의미는 서로 다르다. Convolution은 원래의 변수가 출력에도 그대로 살아있는 연산의 일종이기 때문에 그 결과가 자신이 속해있는 공간 그 자체로 보내지게 된다. Correlation은 원래의 변수가 다른 반수로 바뀌어 출력에 나타는 변환의 일종이기 때문에 그 결과가 자신이 속한 공간이 아닌 다른 공간에 보내지게 된다. 즉, convolution은 다른 특별한 용도를 위해서 수학적인 도구 역할이 강조가 되고, correlation은 유사성의 비교 척도로 활용이 된다.

Gathering vs. Scattering

그렇다면 어떻게 convolution이 동작하는 2가지의 방식에서 살펴보도록 할 것이다.
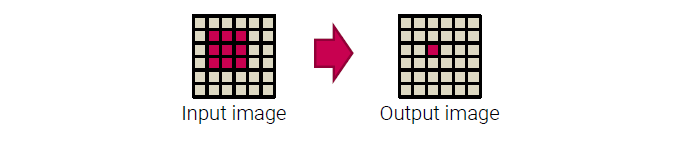먼저 gathering은 여러 픽셀로부터 원하는 연산을 통해서 하나의 픽셀값을 결정하도록 하는 것이다. 하나의 픽셀값을 결정하기 위해서 해당 위치의 픽셀과 이웃한 여러 개의 픽셀을 이용해서 계산을 진행하게 된다.
다음의 scattering은 하나의 픽셀로부터 원하는 연산을 통해서 여러 픽셀값을 결정하도록 하는 것이다.

Fundamental Properties

Convolution과 correlation도 수학의 연산에 해당하기 때문에 수학적인 성질을 가지고 있다. 분배 법칙은 두 연산 모두 해당하지만, 결합 법칙과 교환 법칙은 correlation은 해당하지 않는 것을 볼 수가 있다.

Seperable Filter

만약에 해당하는 filter가 row와 column의 곱으로 표현이 가능하다면 지금까지 살펴 본 2차원 filter의 경우 separable하여 분해가 가능해진다.
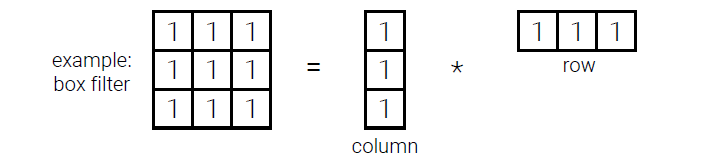위의 예시는 모든 filter의 값이 1인 box filter를 예로 들었으며, 이 filter같은 경우에는 모든 row와 column의 값이 1로 분해가 가능하다. 여기서 곱의 의미를 생각해 볼 수가 있는데, 첫번째로는 matrix multiplication의 관점이 있고, 두번째로는 convolution operation의 관점이 있다. 이미지에 적용하는 filter라는 것에서 두번째 관점이 적절할 수 있으나 사실 어떻게 해석해도 무방하다.

모든 2차원의 filter가 separable하지 않고, 특정한 경우에만 가능하다. 그렇기 때문에 spatial한 특성을 가지고 있고 중요하게 생각해 볼 수 있는 것이 바로 rank이다. Rank는 선형 대수에서 배울 수 있는 행렬 개념으로, filter matrix에서 생각해 보면 rank가 1인 경우가 가지는 의미가 상당하다. 위의 예시도 rank가 1인데, rank가 1이라는 것은 하나의 row가 scale이 결정이 되어 다른 row로 전환이 가능한데, 쉽게 말해서 rank가 1인 2차원의 filter만이 분해가 가능해진다.

그렇다면 separable한 filter가 가지는 장점이 무엇일까? 바로 연산량에 있다. 만약 $M\times M$ 픽셀을 가지는 이미지와 $N\times N$의 크기를 가지는 filter가 있을 때, non-separable한 filter라면 연산량이 $M^2\times N^2$가 되고 seperable한 filter라면 연산량이 $2\times N\times M^2$이 된다. 만약의 kernel의 사이즈가 커지게 된다면 연산량의 차이도 커지게 되어 효율성의 측면에서 체감이 클 것이다.

Gaussian Filter

다음 이미지는 원본에다가 box filter를 적용한 결과이다.
혹시 어떠한 문제점을 찾았는가? 결과를 자세히 보면 원래 사진에는 없던 흐릿한 선들이 많이 보이는 것을 알 수가 있다. 우리는 이 선을 ghost line으로 부를 것이며, 원래 원본에는 없는 선들을 말한다. Box filter를 이용해서 high frequency를 제거하려고 한 것인데, smooth해졌다기 보다는 이상해진 결과를 얻어버린 것이다. 그 이유는 바로 box filter의 모양 때문이다.

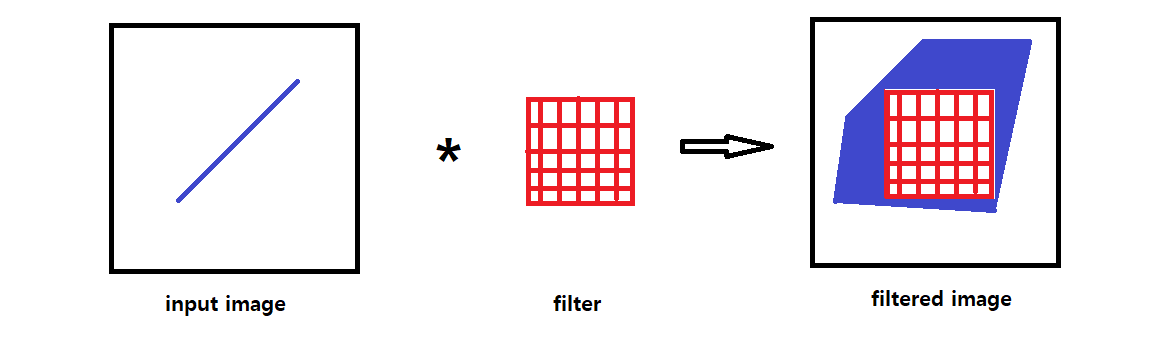0이 아닌 같은 값의 box filter를 이용하게 되면 원래 ghost line이 없었는데, 많은 ghost line을 만들어 버리게 되는 것이다. 그렇기 때문에 filter의 적절한 보완이 필요하다. 그래서 등장한 filter가 바로 Gaussian filter이다.

만약 위와같이 디테일한 부분을 없애고 smooth한 이미지를 만들고 싶다면 Gaussian filter를 사용하면 된다. Gaussian filter는 가장 대표적인 lowpass filter로, kernal의 값이 이름 그대로 2차원의 Gaussian 함수로부터 결정이 된다.

Filter의 중심 값은 가장 큰 값으로 설정이 되어 주변부로 나갈수록 값이 Gaussian 함수에 의해서 줄어드는 것이 Gaussian filter의 특징이다.
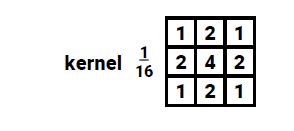Guassian filter의 값은 보통 $\sigma$에 의해서 결정이 되는데, 이 값이 클수록 kernel의 값들이 커져서 더 큰 kernel을 만들게 된다. 보통은 $\sigma$의 2배나 3배가 되는 값을 선택해서 kernel을 만들어 사용한다.

Gaussian vs. Box Filtering

그래서 box filtering의 문제점을 해결하는 Gaussian filtering을 알아보았고, 이를 원본 이미지에 적용한 결과를 다음의 예시를 통해서 살펴볼 수 있다.
Box filter를 사용하면 ghost line이 선명하게 드러나는 반면에, Gaussian filter를 사용하면 high frequency component를 효과적으로 제거해서 더 smooth하고 자연스러운 결과를 낼 수가 있다.

Sharpening Filter

Sharpening filter는 원본 이미지를 선명하게 만들 때 사용한다. 방식은 간단한데, identity filter에서 lowpass filter를 빼면 highpass filter가 된다. 우리는 blurry하게 만들기 위해서 lowpass filter를 사용했었고, 이번에는 반대로 선명하게 만들기 위해서 highpass filter를 사용할 것이다.
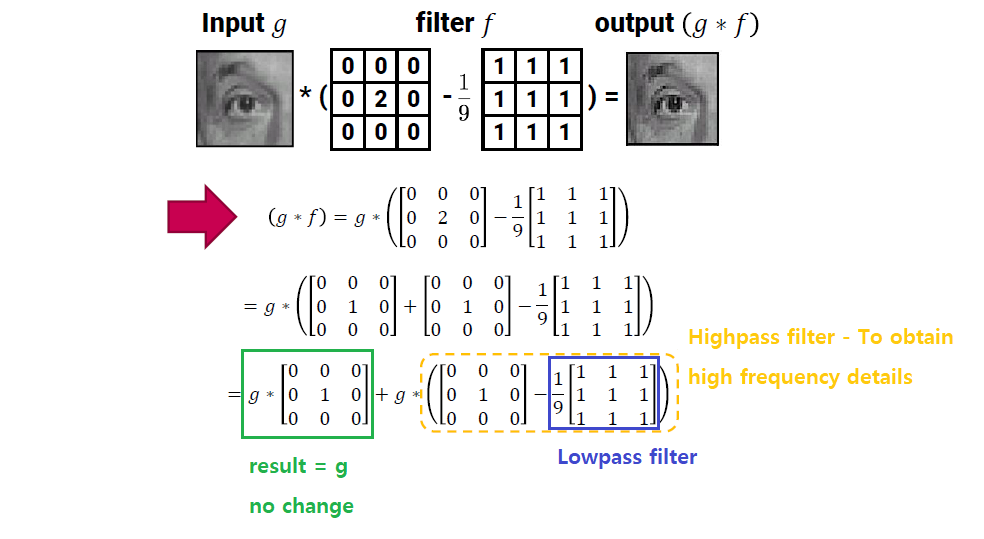이미지를 선명하게 만들기 위해서는 unsharp masking의 작업이 필요하다. 이 작업은 filter를 이용해서 이미지를 더욱 선명하게 만들어 주는 것을 말하며, 해당 식은 다음과 같다.

$I_{out}$은 filter를 적용한 결과 이미지이고, $I_{in}$은 원본 이미지, $\alpha$는 sharpening의 정도를 결정할 수 있는 factor, $F$는 filter, $F * I_{in}$는 선명하게 이미지를 만들기 위한 filtering을 적용한 디테일이다. 여기서 $F$는 highpass filter 혹은 bandpass filter를 사용하게 된다.

high-pass filter: $F = Id - G$
band-pass filter: $F = G_{small} * (Id - G) = G_{small}-G_{large}$

Sharpening filter를 사용할 때 주의해야 할 점은 너무 과하지 않은 선에서 적당하게 조절하는 것이 중요하다.
너무 과하게 sharpening을 진행하게 되면 사진이 어색하게 보이거나 자연스럽지 않은 결과를 만들게 된다.