이번에는 sampling에 의해서 발생하는 aliasing의 의미를 이해하고, 이러한 현상을 어떻게 피하고 막을 수 있는지 알아볼 것이다.
Sampling
이미지를 획득하는 과정 속에서 우리가 하고 싶었던 일은 continuous 데이터들로부터 digital 데이터를 만들어내는 것이다. 데이터를 센서로 부터 얻게 되면 보통은 continuous 데이터를 얻게 된다.
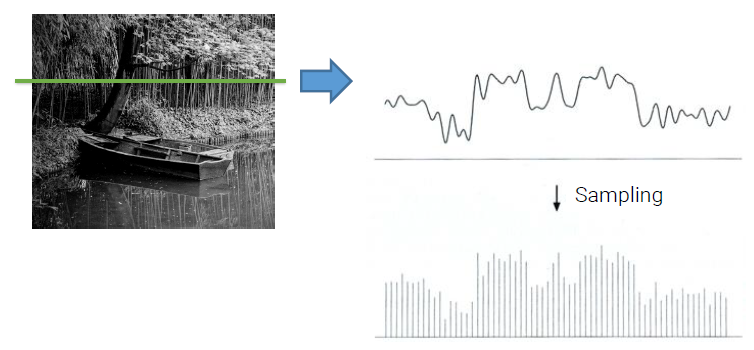카메라를 이용해서 어떠한 사진을 찍었다고 생각해보자. 이 사진의 우리는 virtual line을 그려서 밝기에 대한 정보를 추출하려고 한다. 하지만 데이터를 추출하게 되면 continuous한 데이터가 추출이 되고, 이는 현실 세계의 정보를 그대로 반영하기 때문이다. 이러한 결과는 우리에게 의미있는 정보를 제공해주지 못한다. 우리가 원하는 것은 일종의 수학적인 정보가 필요한 것인데, continuous한 데이터를 통해서는 그 정보를 얻기가 힘들다. 그래서 이러한 데이터를 compact한 방법으로 바꿔줄 필요가 있다. 이러한 과정이 바로 sampling이라고 한다. Sampling은 기본적으로 무한한 continuous 데이터들에서 유한한 데이터를 얻어내는 과정을 말한다.
수학적에서 sampling이라고 하면 모집단 전체의 수많은 데이터와 정보를 사용하면 비효율적이기 때문에 최소한의 의미있는 정보를 위해서 적당한 수의 데이터를 뽑아서 전체 모집단의 성질이나 패턴을 추정하기 위한 행동이다. 이러한 의미가 이미지 관점에서도 다르지 않다. 데이터가 2차원으로 늘어났을 뿐, 그 의미는 같다.
Reconstruction
우리는 앞서 continuous 데이터를 digital 데이터로 바꿔주는 sampling에 대해서 알아보았다. 그리고 우리는 이러한 sampling을 진행하여 얻은 digital 데이터를 다시 continuous analog 데이터로 원상 복구 시킬 수 있어야 한다.
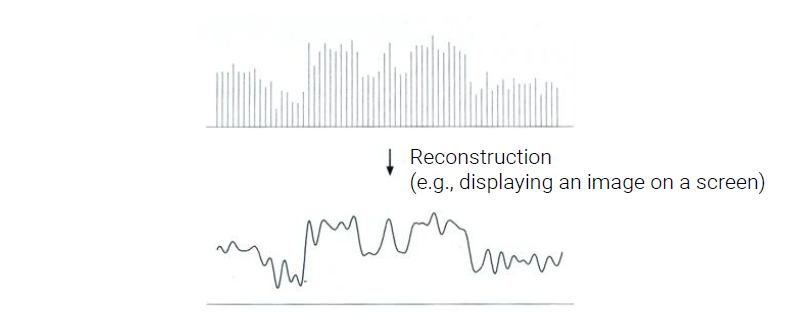Sampling을 진행하여 얻은 digital 데이터를 다시 continuous analog 데이터로 바꿔주는 행동을 reconstruction이라고 한다. 이러한 reconstruction은 인간의 뇌에서 어떠한 물체나 풍경을 받아들일 때 같은 역할을 한다.
Example of sampling and reconstruction
그러면 다음의 예시를 보자. 다음의 예시는 1차원 데이터로 우리가 소리를 듣는 과정에 대한 것이다.
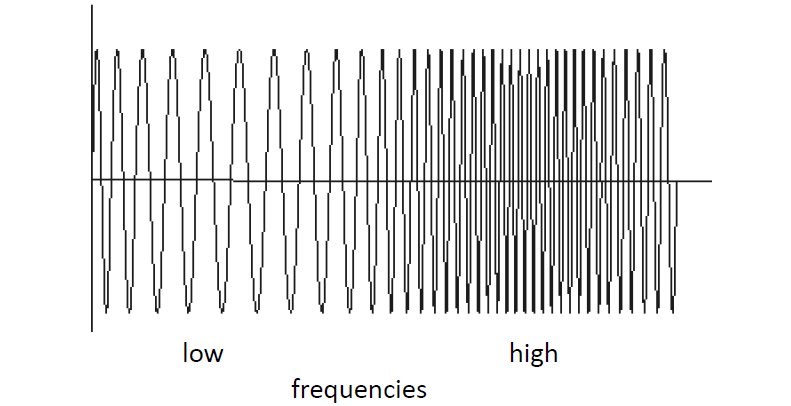소리는 공기의 진동에 의해서 사람에게 전달이 된다. 진동이 빠르게 되면 높은 진동수를 발생시키는데, 진동수가 높으면 높은 음역대의 소리가 전달이 된다. 반대로 진동이 느린 속도로 생기면 낮은 진동수가 발생하여 낮은 음역대의 소리가 전달이 된다.
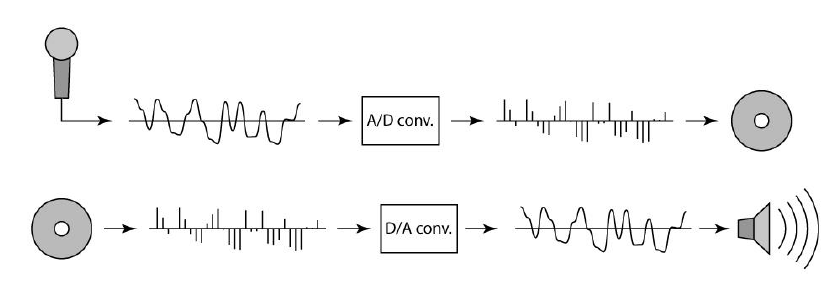우리는 이러한 소리를 녹음을 진행하고, 이를 다시 들어보게 될 것이다. 마이크를 이용해서 소리가 전달이 되면 analog 데이터가 전달이 될 것이다. 이러한 continuous 데이터는 A/D converter에 의해서 digital 데이터로 변환이 되어 디스크와 같은 저장 매체에 저장이 될 것이다. 그러면, 이 디스크로부터 발생하는 digital 데이터를 다시 D/A conveter를 통해서 anlog 데이터로 변환시켜 재생할 수 있다.
Undersampling
만약에 sample한 결과에서 놓친 부분이 있다면 어떻게 해야할까? 다음의 sin wave를 보자.
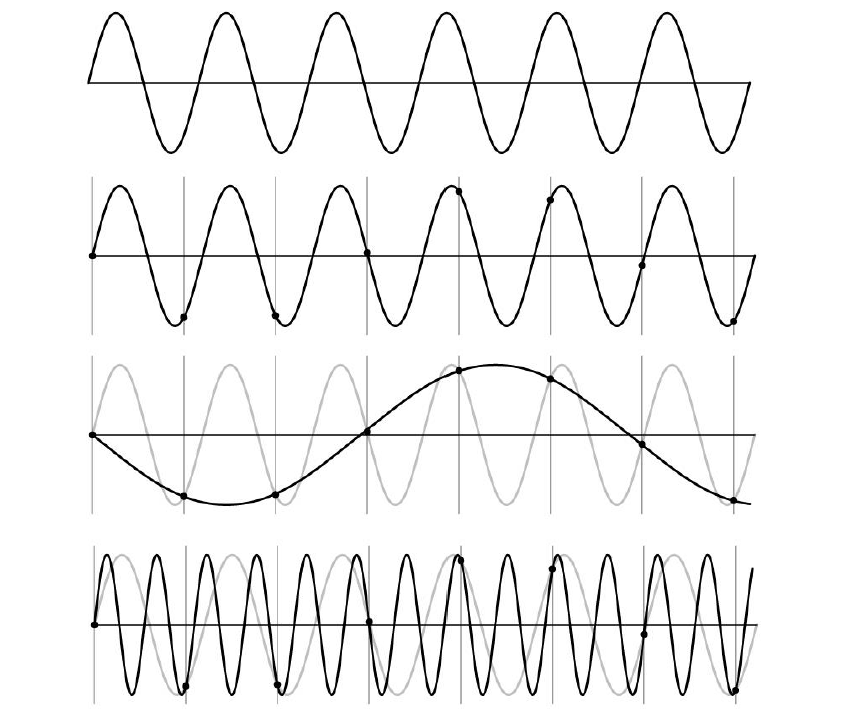이 wave에서 몇 개의 점을 sampling 할 것이다. 그리고 sampling이 된 이 점들을 interpolate하게 되면 다른 모양의 wave가 만들어진다. 그 결과는 기존의 정보와는 완전히 다른 정보가 될 수 있다. Sampling이 된 점들이 원래의 wave보다 낮은 주파수인지, 높은 주파수인지는 알 수가 없다.
Undersampling은 filtering이 된 데이터에 대해서 알고 있고, sampling이 된 주파수보다 높은 데이터라도 그 데이터를 완전히 복원하거나 사용할 수 있는 sampling을 말한다. Sampling에 under라는 단어가 붙은 이유도 보다 높은 주파수의 신호라도 낮은 주파수로 나타나기 때문에 붙여진 것이다.
Aliasing
Sampling 과정에서 주파수가 원본 데이터의 최대 주파수의 2배보다 낮은 경우에 output이 왜곡이 되는 현상이 나타는데, 이를 aliasing이라고 한다. 이러한 aliasing은 이미지나 영상에서는 계단 현상이라는 것을 만들게 된다. 이미지의 크기를 줄일 때, 몇개의 픽셀에 대한 정보가 사라지게 된다. 픽셀이 사라지게 되어 남은 픽셀들이 일종의 계단 모양을 만들게 되는데 이러한 현상을 aliasing이라고 하는 것이다.
우측의 사진(Zone plate chart)을 보면 가운데에 큰 원이 있고, 주변으로 다른 원들이 보인다. 이 원들은 주파수를 나타나게 되는데, 카메라의 성능이나 해상도와 관련해서 일종의 실험을 할 때 사용이 된다.
가령, 게임에서 고사양이었던 화질을 저사양으로 낮추게 되면 aliasing 현상이 발생하게 된다. 그러면 이미지에서는 최대한 많은 데이터를 보전해야하는 작업이 필요해지게 되는 것이다.
Antialiasing
만약, 이미지에 aliasing이 생기게 되면, 이를 보정해주는 작업이 필요하다. Alias들을 줄이는 기술들이 몇가지 존재하는데, 가장 대표적인 방법이 antialiasing이다. Antialiasing이 어떤 하나의 기술을 이야기하는 것은 아니지만, 대표적으로 alias를 해결할 수 있다.
첫번째로 직관적인 방법으로 sample을 더 많이 하는 것이다. Sampling 하는 점들을 더 많이 늘리면 alias를 줄이는 효과가 발생하게 된다. 그러나, 이러한 방법이 사실 실현하기에는 어려움이 존재한다. Sample을 더 많이 얻기 위해서는 photodiode의 크기를 줄여야만 한다. 그리고 이는 추가적인 sensor technique을 요구하게 된다. 애초에 사진을 찍는 카메라의 사양도 바꿔야하는 것이다. 또한, 이러한 방법은 단지 문제를 높은 주파수대로 옮기는 정도로밖에 되지 않기 때문에 실질적인 해결책이 되지 못한다.
두번째로는 신호 자체를 덜 wiggly하게 만드는 것이다. 우리는 신호를 가져오려고 할 때, 높은 주파수는 제거할 수 있다. 그러면 높은 주파수에서 주로 발생하는 alias를 피할 수 있다. 그러나 이 방법도 또한 결점이 있다. 이 방법은 신호로부터 정보를 잃어버릴 수 있다. 그래도 이 방법이 aliasing보다는 낫다. Aliasing은 이미지의 퀄리티를 상당히 망치기 때문이다. 그렇기 때문에 정보를 조금 잃어버리더라도 aliasing보다는 괜찮다는 이야기이다.
두번째 방법을 좀 더 디테일하게 살펴보면, lowpass filter를 사용하면 된다. Lowpass filter의 역할은 안전하고 낮은 주파수를 남겨놓고 높은 주파수를 제거해준다.
Lowpass filter는 카메라의 lens와 sensor 사이에 위치한다. 창문의 먼지라고 생각해도 된다. 창문에 먼지가 있으면 완벽하게 물체를 볼 수가 없기 때문이다. 이 filter를 통해서 높은 주파수를 제거하고, aliasing을 막을 수 있다.
최근에는 카메라에 이 filter를 잘 사용하지는 않는다. Photodiode의 수가 최근에는 충분히 많이 있기 때문이다. 그래서 lowpass filter 없이도 aliasing을 막을 수 있으며, 그렇기 때문에 정보의 손실도 함께 막을 수 있다.
Image Sub-Sampling
커다란 이미지가 있다고 생각하고, 이 이미지를 스크린에 띄워보려고 하자. 그런데 이미지가 너무커서 스크린에 알맞게 띄우기가 어렵다. 그래서 사진의 크기를 줄여서 스크린에 알맞게 보여주려고 한다.
그래서 이미지를 반으로 계속 줄여나가면서 row와 column의 반을 날려버렸다. 이를 image sub-sampling이라고 한다. 그런데 이렇게 이미지를 반으로 줄이면서 픽셀 정보를 날려버리면 문제가 발생한다.
바로 이미지가 자연스럽게 보이지 않는다는 것이다. 반으로 계속 줄이면서 이미지 정보가 손실이 되었고, 그렇기 때문에 이미지는 원래보다 더러워지고 이상해지게 된다. 이러한 현상이 이미지에서의 aliasing이다.
Image Pre-Filtering
그래서 이를 해결하기 위해서 lowpass filter를 이용할 수 있다. Sub-sampling을 하기 이전에 Lowpass filter를 사용하게 되는데, 여기서는 Gaussian lowpass filter를 사용했다. Gaussian lowpass filter는 가장 대표적인 lowpass filter이고, 이를 sub-sampling 전에 사용하게 되면 문제를 해결할 수 있다.
그러면 더이상 이미지가 기괴해지는 것을 막을 수가 있다.
그리고 이를 다시 resize해서 확인해보면, lowpass filter를 사용하기 전보다 더 자연스러워지는 것을 볼 수가 있다. 우선 자연스러워지기 때문에 aliasing을 해결했다고 볼 수 있다. (Gaussian lowpass filter가 정확이 무엇인지는 다음 주제인 image filtering에서 다뤄볼 예정이다.)
Gaussian Image Pyramid
계속해서 filtering과 sub-sampling을 진행했을 때, 이미지의 크기는 계속해서 달라지게 된다. 이렇게 Gaussian filter를 이용하고, 이미지의 크기가 달라져서 만들어지는 피라미드 형식을 Gaussian image pyramid라고 한다.
Gaussian image pyramid는 여러 분야에서 사용이 된다. Computer graphics, computer vision 분야나 wavelet transform 분야 등에 널리 사용이 되고 있다. 노이즈를 제거할 때 주로 사용이 될 것이다. 이 방법을 통해서 달라지는 주파수마다 적용되는 피라미드를 만들기 때문에 효과적일 수 있다. 다른 적용 예시를 보자.
Gaussian image pyramid는 object detection이나 recognition 등에서도 효과가 좋다. 사람이나 동물의 얼굴을 detection한다고 생각하자. 사람의 얼굴이 크게 나올 수도 있고, 사람이 많아서 작게 나올 수도 있을 것이다. Face detection을 큰 얼굴에서 적용했을 때, 작은 얼굴에는 적용이 잘 안 될 것이다. 이때 image pyramid를 만들어서 sub-scale의 이미지를 이용할 수 있는 것이다.
이러한 image pyramid의 장점은 search할 때 더 나은 방법으로 search가 가능하다는 것이다. Translation이나 scale이 달라져도 적용이 가능하기 때문이다. 그리고 pre computation을 통해서 다른 해상도의 texture을 mapping하는 분야 등에 유용하게 사용이 된다.
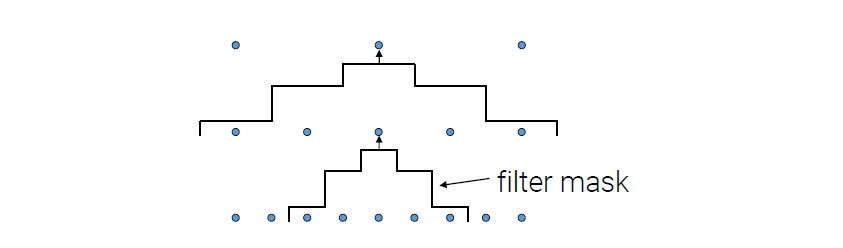Gaussian pyramid를 만들기 위해서는 굉장히 간단한 반복 과정만 진행해주면 된다. Filter를 취하고, sub-sample만 해주면 된다. 이 과정을 반복해서 도달할 수 있는 가장 작은 해상도까지 이미지의 크기를 줄여가면서 피라미드를 만들면 된다. 이미지나 적용하려는 분야에 따라서 3-level이 될 수도 있고, 7-level이 될 수도 있는 것이다.
만약, 이미지를 1/4로 줄여나간다고 생각하면, 피라미드의 전체 크기는 1+1/4+1/16+...를 해서 4/3을 넘지 못하게 될 것이다. 원래의 이미지 보다 크게 벗어나지 않게 된다.
