[계산사진학] Image Filtering - Non-linear Filtering

Order-Statistics Filters

Order-statistics filter는 non-linear한 spatial domain filter 중 하나이다.
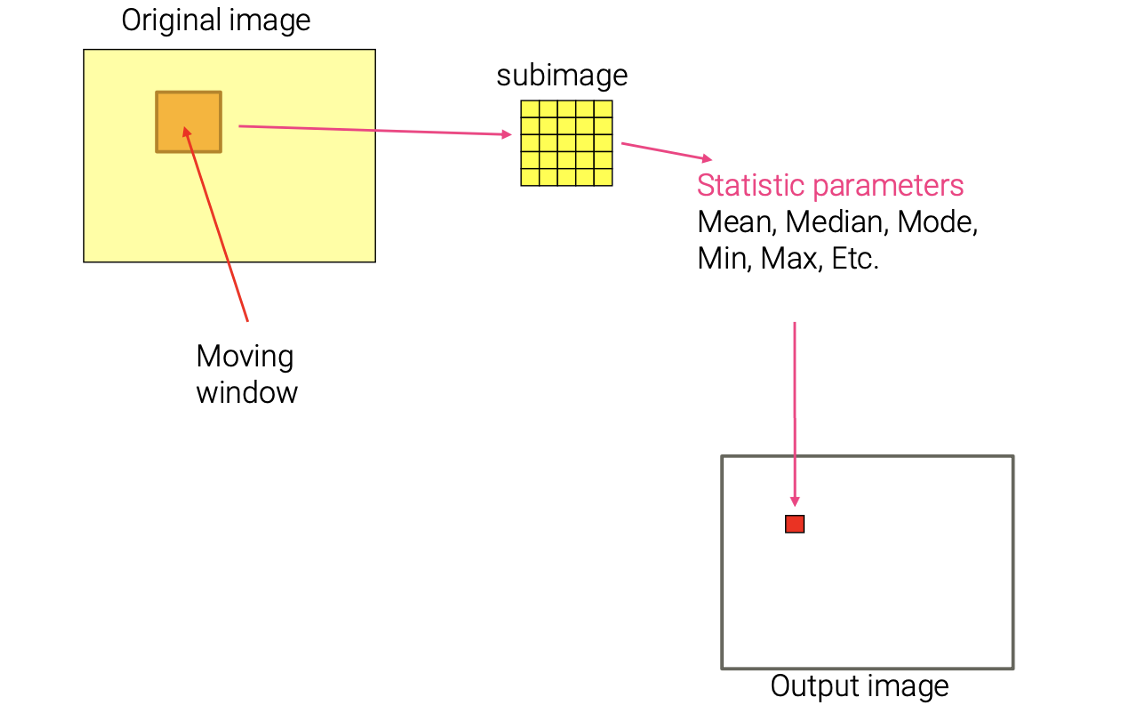Linear filtering에서의 과정과 마찬가지로 원본 이미지 상에 filter를 사용해서 sliding을 시키면서 픽셀 값을 계산하여 결정해주면 된다. 다만, 차이점은 linear filtering에서는 linear combination을 할 수 있도록 filter를 구성하지만, order-statistic는 filter를 linear combination이 아닌 mean, median, mode, min, max 등의 linear 하지 않은 계산을 통한 결과를 통해서 픽셀 값을 결정하게 된다. Mean은 평균 값, median은 픽셀들을 정렬시켰을 때 중간 값, mode는 데이터로부터 가장 많이 등장하는 값, max나 min은 최대, 최솟값을 선택하는 것이다. 이는 상황에 맞게 filter의 목적을 설정해서 filtering을 진행하면 된다. 일종의 통계학적인 개념을 filter에 사용해서 새로운 픽셀 값을 결정하는 것이다.

Median Filter

많고 많은 non-linear filter 중에서 가장 대표적으로 잘 알려져 있는 median filter를 알아보려고 한다. Median filter는 이미지 상에서 salt-and-pepper noise가 많을 때 효과적으로 사용할 수 있는 filter이다. 다음의 이미지를 살펴보자.
이미지를 잘 보면 깨끗하지 못한 것을 알 수가 있다. 이미지 곳곳에 하얀 점들이나 검은 점들이 많이 분포하여 이미지를 지저분하게 만든 것을 볼 수가 있다. 이는 이미지를 얻기 위하여 사용한 사진기의 물리적 문제로 인해서 발생하는 것이다.

그럼 salt-and-pepper noise가 무엇인지 알아보겠다. 먼저 salt noise는 이미지 상에서 하얀 색의 픽셀이 무작위로 분포하는 것을 이야기하며, pepper noise는 이미지 상에서 검은 색의 픽셀이 무작위로 분포하는 것을 이야기한다. 이 둘을 합쳐서 salt-and-pepper noise라고 하는 것이다. 그럼 위의 이미지에서 median filter를 사용한 결과를 보자.
$3\times 3$ median filter를 사용하게 되면 이미지가 깨끗해진 것을 육안으로 확인이 가능하다. Median filter는 특정 구간에서의 픽셀 값들을 작은 값부터 큰 값으로 정렬했을 때, 중간 값을 골라서 output 이미지에 픽셀 값으로 결정하게 된다. 그러면 이전에 발견되던 noise들을 지울 수가 있으며 효과적인 filtering이 가능해지게 된다. 전통적인 lowpass filter는 이러한 noise에 효과적이지 못했지만, median filter와 같은 non-linear filter는 이러한 noise에 효과적인 것을 확인한 셈이다.

Highpass, Bandreject, and Bandpass

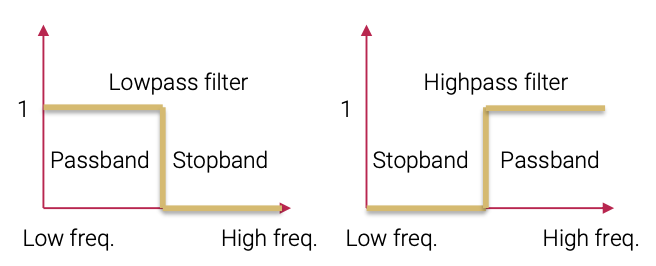
지금까지 lowpass filter와 highpass filter를 통해서 그 성격과 특징들을 살펴보았다. 먼저 low frequency component는 lowpass filter를 통해서 이미지를 smooth하게 만들었고, 이때는 이미지의 디테일적인 부분은 고려하지 않게 된다. 반대로 high frequency component는 highpass filter를 통해서 이미지를 디테일하게 만드는데, highpass filter는 원본에서 low frequency를 빼주는 연산을 통해서 얻을 수 있었다.
이번에는 bandreject filter와 bandpass filter에 대해서 알아보려고 한다.
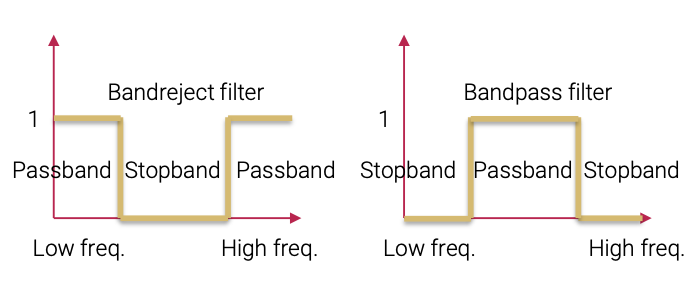먼저 bandpass filter는 오로지 특정한 범위의 intensity 값만 통과시키는 filter로 너무 low하고 high한 frequency의 범위는 통과시키지 않는다. 그리고 이와는 반대로 특정 범위를 제외하고 low하고 high한 frequency의 범위만 통과시키는 filter가 bandreject filter이다. 그러면 이 filter들을 수학적으로 정의한 것을 살펴보자.
먼저, lowpass filter는 $lp(x,y)$로 정의하고 시작하겠다. 다음으로 highpass filter는 $hp(x,y)=\delta(x,y) - lp(x,y)$로 정의할 수 있는데, 이때 $\delta(x,y)$는 identity filter로 모든 frequency를 통과시키는 filter라서 원본 이미지로 해석이 가능하고, 여기서 lowpass filter와 마이너스 연산을 통해서 highpass filter를 정의할 수 있다. Bandreject filter는 $br(x,y)=lp_1(x,y)+hp_2(x,y)=lp_1(x,y)+[\delta(x,y) - lp_2(x,y)]$로 정의하게 된다. 이를 해석하면 lowpass filter와 highpass filter를 합친 결과를 나타내게 된다. Bandpass filter는 bandreject filter의 반대이기 때문에 $bp(x,y)=\delta(x,y)-br(x,y)=\delta(x,y)-[lp_1(x,y)+[\delta(x,y)-lp_2(x,y)]]$가 되는 것이다.