[계산사진학] Intensity Transformation

Spatial Domain Processing

Spatial domain은 이미지에서 픽셀들이 존재하는 일종의 공간이라고 생각하면 된다. 우리는 spatial domain technique을 통해서 직접적으로 이미지 상의 픽셀들을 조작하고 변형할 것이다. 이미지는 픽셀들의 집합으로 이 픽셀들의 값을 변형시킴으로써 이미지의 분위기나 형태를 바꿀 수가 있다. 가장 직관적인 방법이지만 이미지에 대한 작업을 할 때 자주 사용이 된다. 그리고 frequncy domain이라 해서 주파수 신호들과 같은 경우에는 이미지로부터 Fourier transformation을 적용해서 조절하게 된다. 이는 뒤에 자세하게 이야기할 것이기에 우선은 spatial domain에 대해서 알아보도록 하자.

위의 식에서 $g(x,y)$는 ouput 이미지, $f(x,y)$는 input으로 사용되는 원본 이미지, 그리고 $T$는 타겟 지점인 (x,y)를 기준으로 주변의 픽셀들로부터 정의가 되는 transformation function이고, 이는 $f(x,y)$를 기준으로 연산이 진행된다.

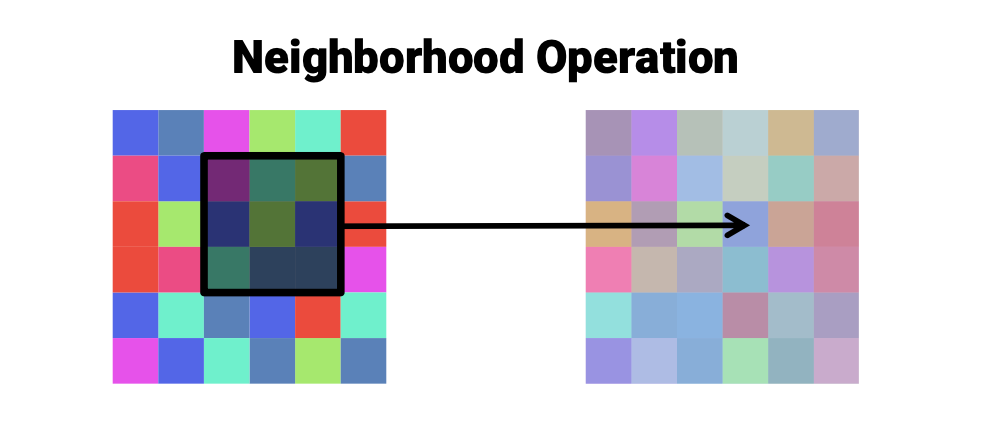좌측의 이미지는 input 이미지로 $f$이고, 우측의 이미지는 ouput 이미지 $g$이다. 하나의 픽셀 값을 결정하기 위해서 좌측의 같은 위치의 픽셀뿐만 아니라 주변의 이웃한 픽셀들까지 이용해서 하나의 픽셀 값을 결정하게 되며, 이러한 과정이 spatial domain processing이다.

Intensity Transformation

Intensity transformation은 spatial domain processing의 하나로, 가능한한 가장 적은 수의 이웃 픽셀들을 이용해서 값을 결정하는 방법이다. 아무래도 이웃이 없이 자기 자신만을 통해서 결정이 되면 가장 작은 경우가 될 것이다. Output의 intensity가 오직 input 이미지의 하나의 픽셀에만 의존하게 된다는 특징이 있다. 그래서 이를 또다른 용어로 point processing이라고 부른다. 그리고 식은 다음과 같다.

$s$는 output intensity, $r$은 input intensity, 그리고 $T$는 intensity transforamtion이다.

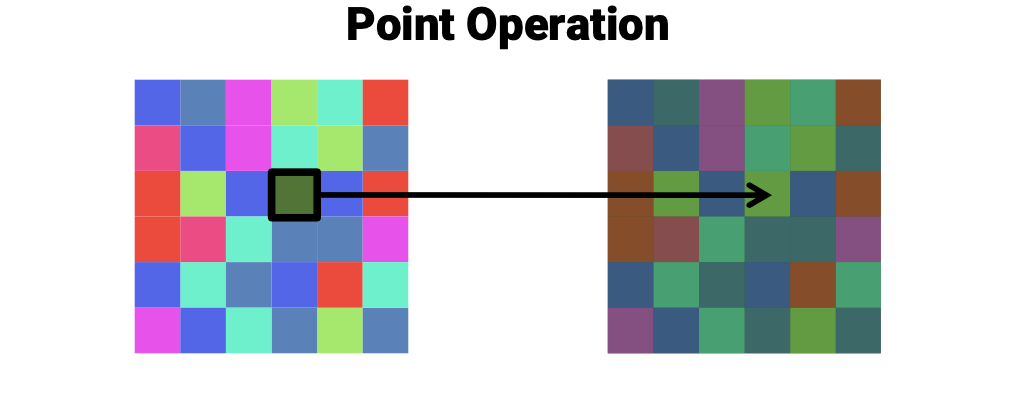다음은 point processing의 몇가지 예시이다. 이를 굳이 외울 필요는 없고 직관적으로 받아들이면 된다. 여기서 만약에 intensity가 0 ~ 255의 범위를 초과하게 된다면 intensity 값은 제대로 visualize가 되지 않을 것이다.

Image Negatives

Image negtive는 intensity를 반대로 바꾼 것을 이야기한다. 반대로 바꾼다는 것은 무슨 의미일까? 0부터 255까지 intensity가 존재할 때, 원래의 intensity x에 대해서 255에서 x를 마이너스 연산을 진행해주면 된다. 그러면 밝은 값은 어두운 값으로, 반대로 어두운 값은 밝은 값으로 바뀌게 될 것이다.
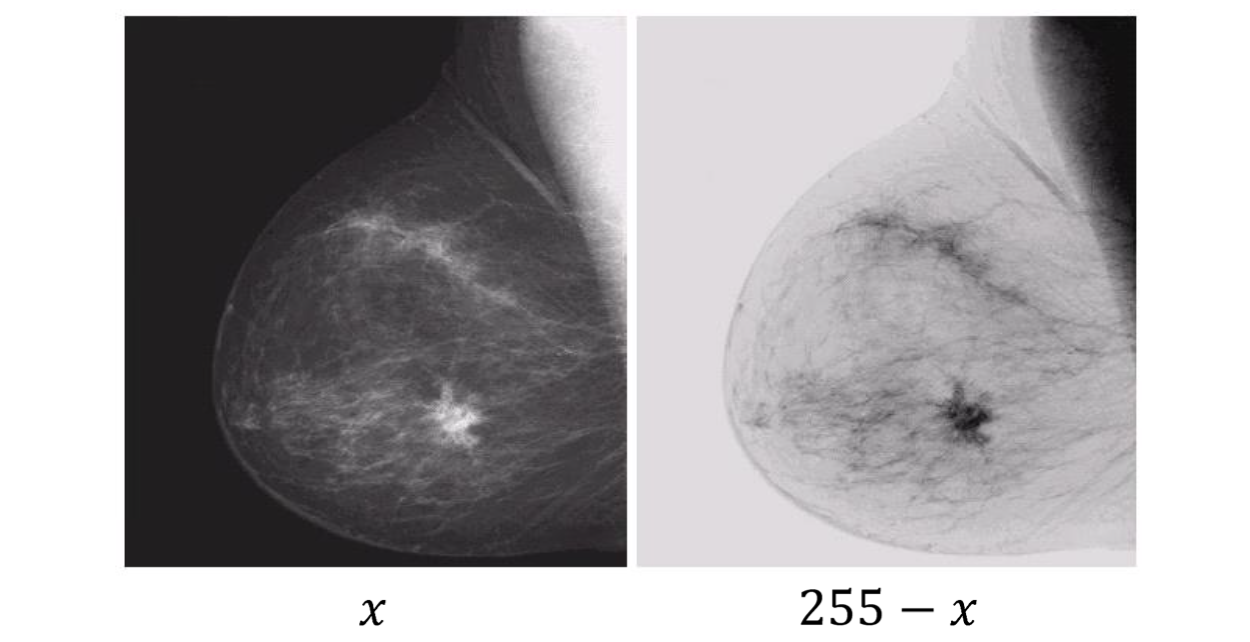이러한 작업을 진행해주는 이유는 무엇일까? 우선 육안으로 위의 두 이미지를 비교해보자. 좌측의 원본 이미지와 우측의 invert 된 이미지를 보았을 때, 아무래도 우측의 이미지가 더 잘 보인다고 생각할 것이다. 인간의 눈이 그렇게 만들어져 있기 때문이다. 어두운 것보다는 밝은 것을 더 잘 인식하게 된다. 그렇기 때문에 invert 연산은 어두운 부분이 지배적일때, 이미지의 어두운 부분을 흰색이나 밝은 회색으로 바꿔주면서 더욱 디테일한 정보를 얻게 해준다.

옛날에 사용하던 카메라 필름을 보자.
Invert 작업을 통해서 intensity를 바꿔줌으로써 사람이나 자동차가 디테일한 부분까지 인식이 되는 것을 확인할 수 있다.

Log Transformations

이번에는 point processing technique의 하나인 log transformation을 알아보겠다. Transformation을 log 식을 통해서 하는 것인데, log의 성질을 반영한 것이다. Log는 값이 작은 구간에서는 변화량이 크지만, 값이 점점 커지게 되면 그 변화량이 점점 줄어드는 성질을 가지고 있다. 이러한 성질을 이용한 것이 log transformation이며 다음과 같다.

$s$는 output intensity, $r$은 input intensity, $c$는 scaling factor로 constant 값이다. 이 값은 output intensity의 범위를 조절하는 역할을 하게 된다. 다음과 같이 특정 구간에 따라서 output intensity의 값이 다르게 변화하는 것을 볼 수 있다.
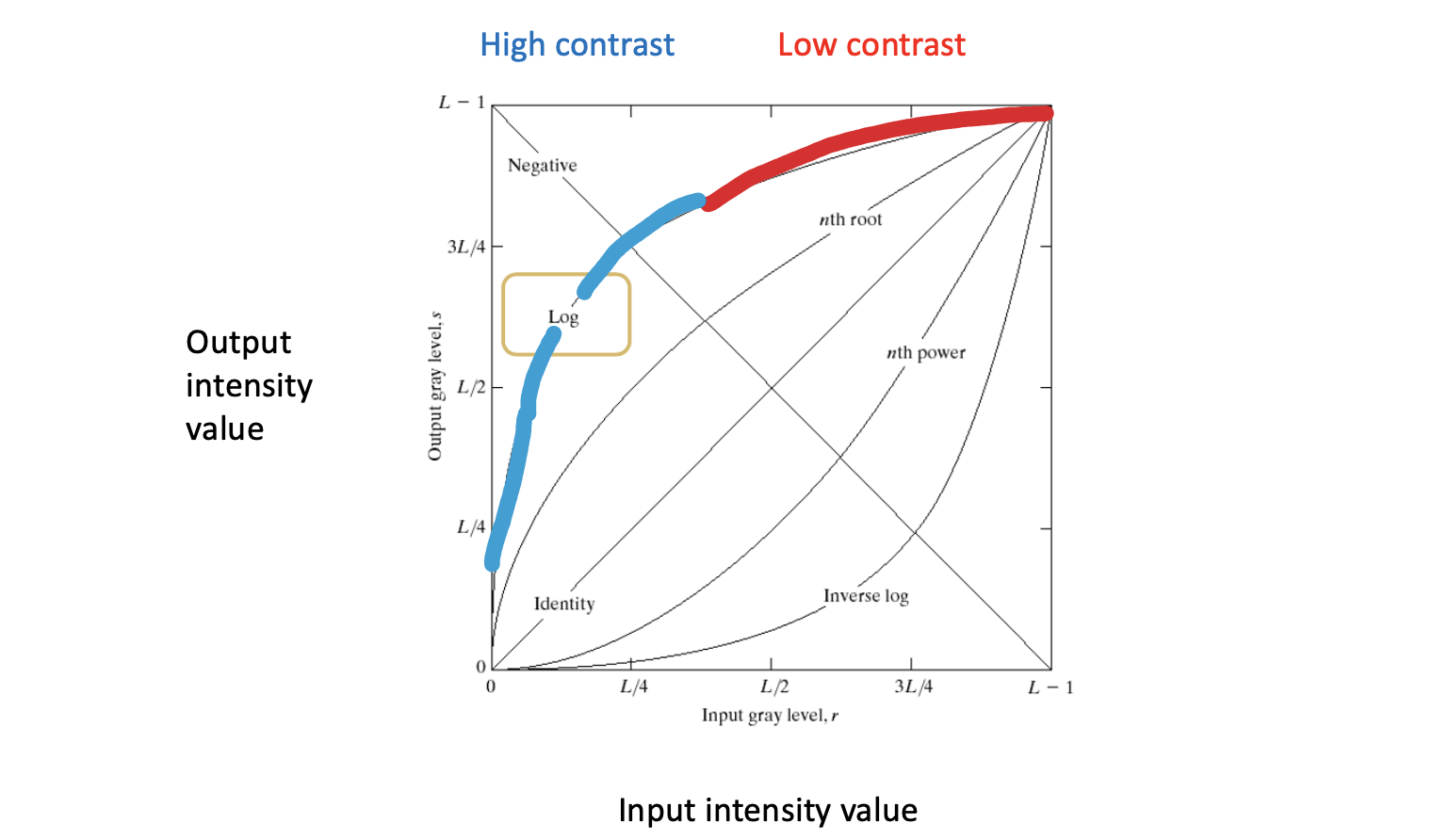그렇다면 log transformation은 보통 어디에 사용이 되는 것일까? 자주 사용되는 경우는 Fourier spectrum을 시각화 할 때이다.
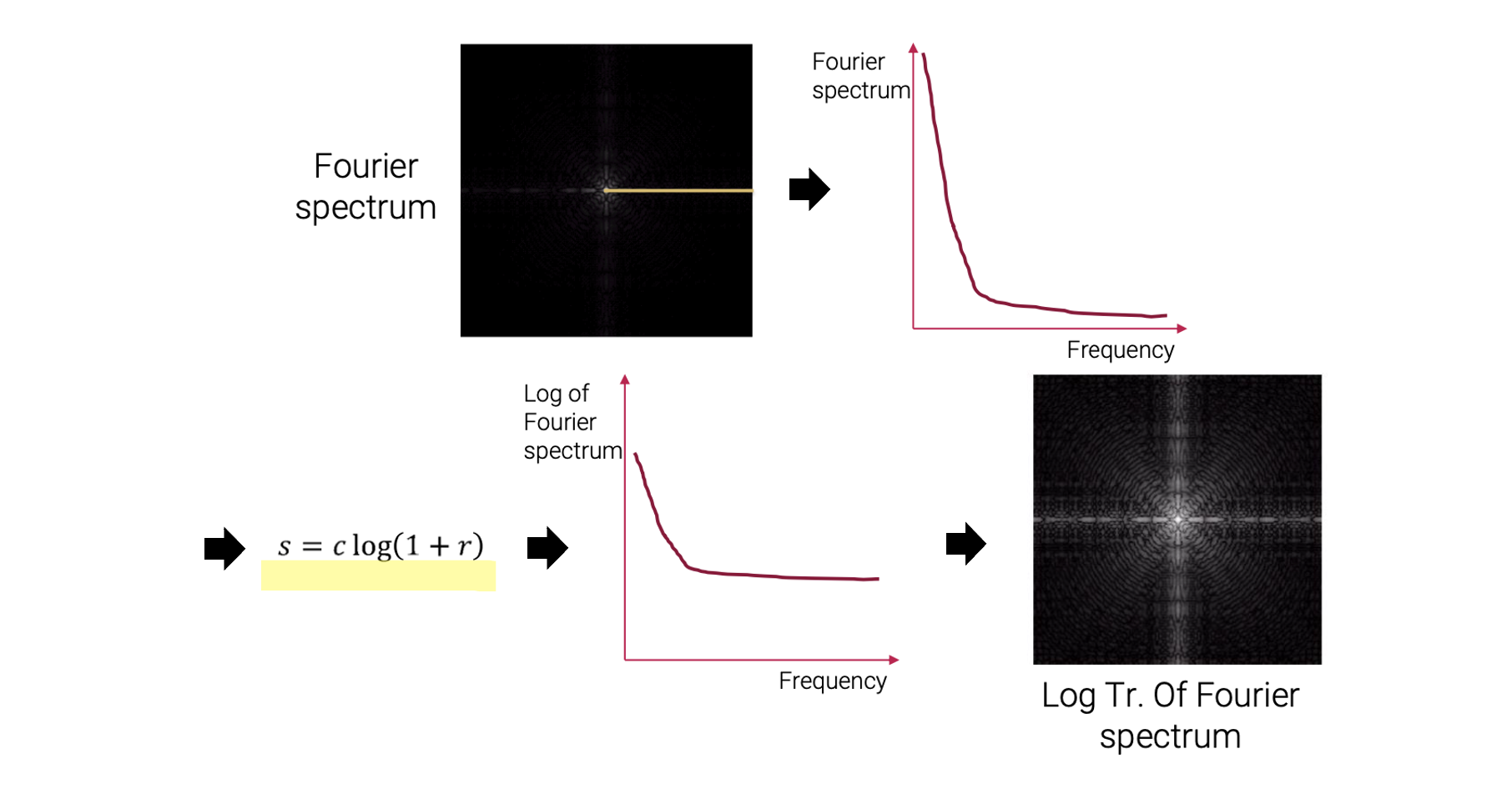이미지를 Fourier transformation 시키면 보통 대부분 검은색의 이미지를 얻게 된다. 이 검은색이 크게 나타나는 이유는 intensity 값들이 가장 큰 intensity에 비해서 너무 작아서이다. 그래서 Fourier spectrum에서 complex 값들을 시각화하는 것은 쉽지 않다. 대신에 절대값을 사용해서 값을 바꾸게 되면 시각화하는데 어려움이 없어지게 된다. 그렇기 때문에 log transformation을 사용하면 더 나은 시각화 결과를 만들게 되면, Fourier transform을 통해서 더 알아보기 쉬워지게 되어 디테일들을 쉽게 찾을 수 있게 된다.

Power-law(Gamma) Transformations

또 다른 transformation으로는 gamma transformation이 있다. 다음의 식은 gamma transformation을 나타낸다.

$s$는 output intensity, $c$는 scaling factor, $r$은 input intensity, 그리고 $\gamma$는 $\gamma$ transforamtion에서 그래프의 모양을 바꿔 다른 효과를 내도록 조절할 수 있는 parameter다. 그래서 $\gamma$ 값에 따른 그래프의 모양은 다음과 같다.
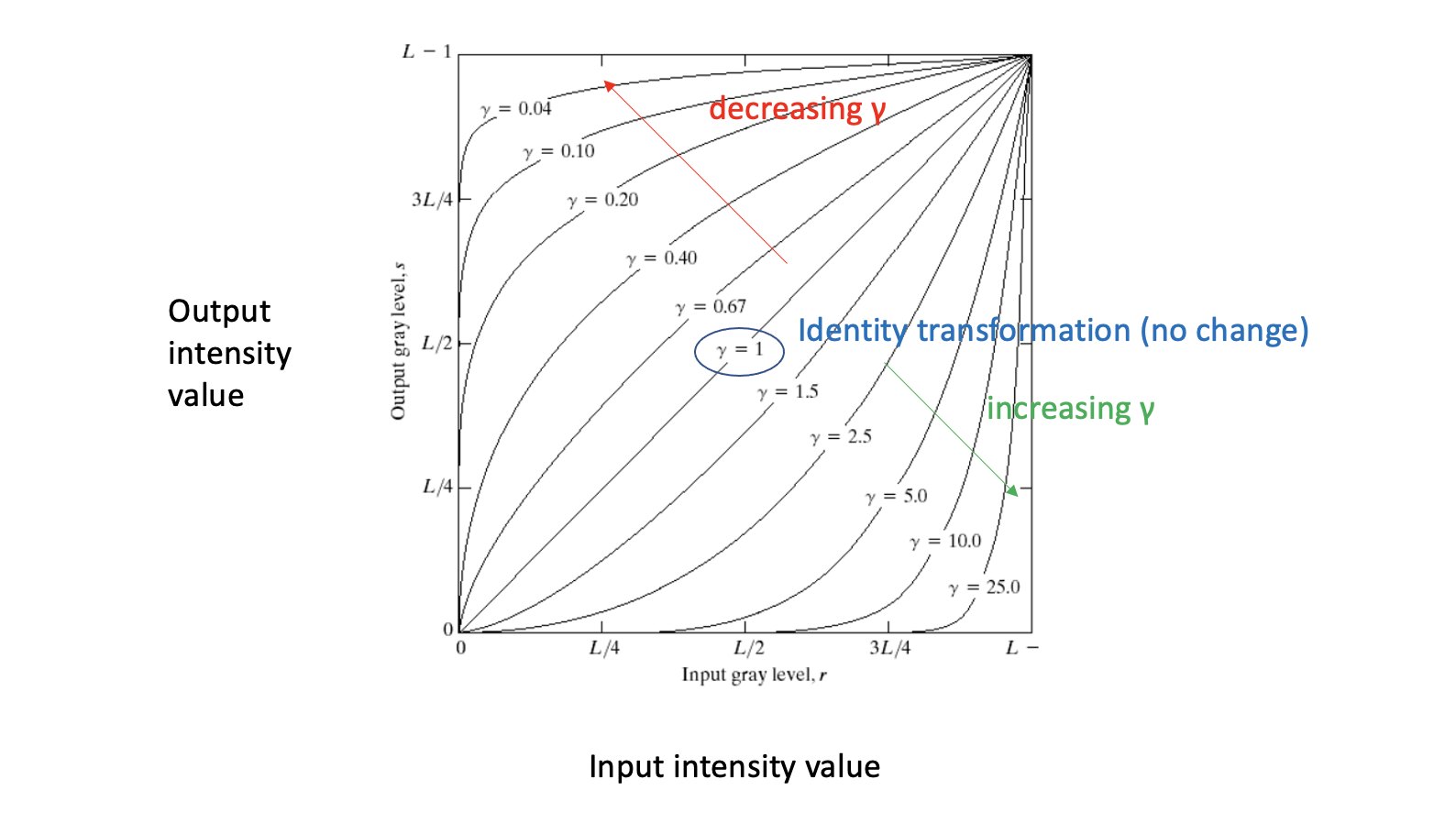예를 들어서 $\gamma$ 값을 1보다 키운다고 생각하자. 1인 경우에는 변화가 없는 linear function이 되어 그대로가 된다. 1보다 커지게 되면 지수 함수의 형태를 하게 되어 255에 가까운 범위에서는 output intensity가 high contrast를 가지게 된다. 즉, 대부분의 input intensity 범위에서 output intensity가 상대적으로 낮게 나와 이미지가 어두워지는 결과를 가지게 될 것이다. 그래서 어두운 이미지에 대해서 밝게 바꾸려면 $\gamma$ 값을 줄일 필요가 있고, 반대로 밝은 이미지에 대해서는 $\gamma$ 값을 키울 필요가 있다. 다음의 예시들을 통해 살펴보자.

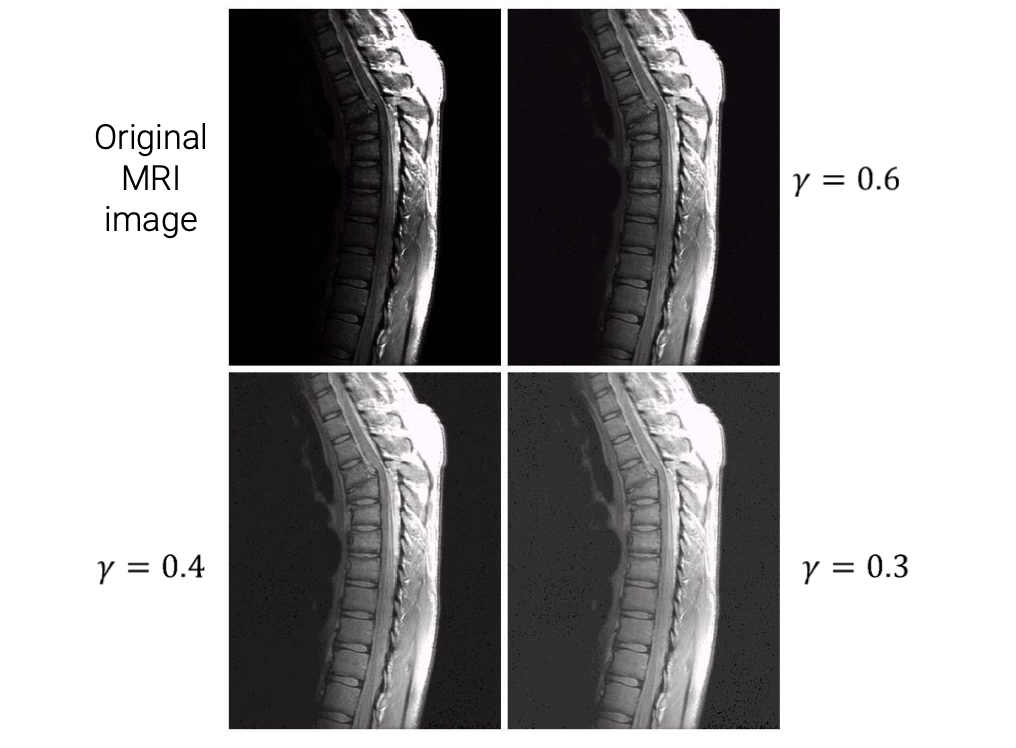원본 MRI 이미지를 보면 어두운 부분이 지배적이라 디테일을 볼 수가 없다. 이때 gamma transformation을 이용해서 $\gamma$ 값을 조절하여 디테일을 더 잘보이게 할 수 있다. 어두운 이미지이기 때문에 brightness를 높일 필요가 있다. 그러기 위해서 $\gamma$ 값을 0.6, 0.4, 0.3 이렇게 낮추게 되면 어두운 부분을 더욱 밝게 나타낼 수 있다. 앞서 $\gamma$ 값을 낮추게 되면 intensity가 작은 부분에 대해서 high contrast를 가지게 만들 수가 있다. 그래서 어두운 부분이 더욱 밝게 보이게 되는 것이다.

이번에는 반대로 밝은 원본 이미지가 있을 때 gamma transformation을 이용한 것이다. $\gamma$을 3.0, 4.0, 5.0 이렇게 키우게 되면 반대로 밝은 부분을 더욱 어둡게 나타낼 수 있다. $\gamma$가 커지게 되면 input 상에서 넓은 range의 범위를 어둡게 나타낼 수 있기 때문이다. 그래서 밝은 부분이라 할지라도 어둡게 표현이 된다.

Gamma Correction

최근에는 LED 모니터나 그 이상의 스펙을 가지는 모니터를 많이 사용한다. 하지만 옛날에는 CRT 모니터라고 해서 뚱뚱한 모니터를 많이 사용했었다. Gamma correction은 가장 두드러지게 사용이 되는 gamma transformation의 하나로, CRT 모니터 상에서 non-linearity 문제를 해결하는데 주로 사용되었다. 정확히 무슨 문제 때문에 CRT 모니터에서 많이 사용이 되었을까? 이미지가 디스플레이 상에서 너무 어둡게 보여 사람들이 육안으로 디테일적인 부분을 볼 수가 없었다. Non-linearity는 물리적인 성질에 의해서 어두워지는 현상을 나타내게 된다. 당시 CRT 모니터에서 non-linearity가 $\gamma=2.2$에 근사했다. 그렇기 때문에 어두운 문제가 발생했고, 이를 해결하기 위해서 gamma correction으로 $\gamma=\frac{1}{2.2}$로 바꿔주었다.
최근에는 CRT 모니터를 거의 사용하지 않는다. 그럼에도 JPEG 이미지 같은 경우에는 여전히 gamma correction을 사용하기 때문에 이 테크닉을 알아둘 필요는 있다. $\gamma$ 값을 적절히 조절하는 것만으로 이미지의 어두운 부분과 밝은 부분을 조절하여 원하는 결과를 만들어 낼 수가 있다.

Contrast Stretching

앞서 contrast가 가장 큰 intensity 갑과 가장 작은 intensity 값의 비율이라고 이야기한 적이 있다. 우리는 이 contrast를 조절하는 함수를 만들어 이미지에 적용시킬 수가 있다. 이때 사용되는 이 함수를 contrast enhancement function이라고 하며, 다음과 같이 input 이미지의 intensity 값들의 분포 상에서 임의로 constrast를 조절하는 함수를 디자인 할 수 있다.

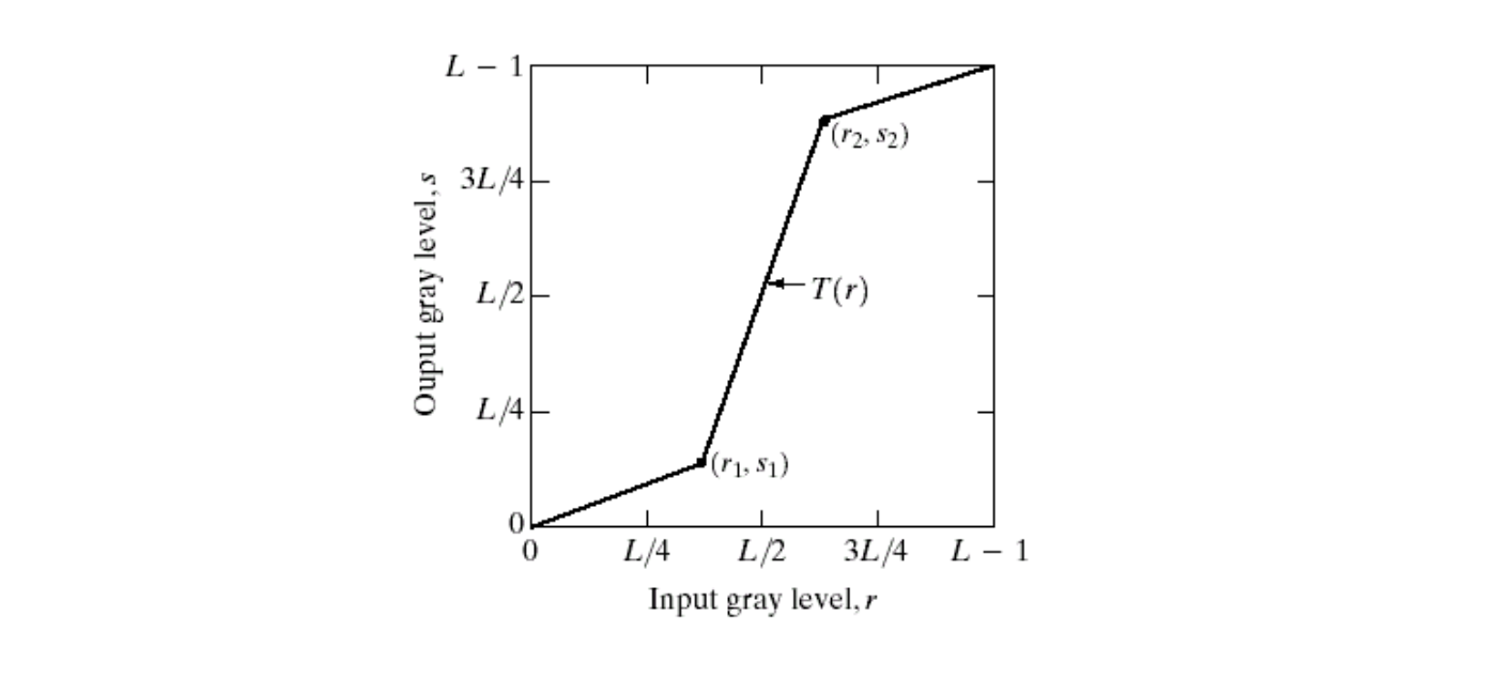위의 함수의 특징은 원본 이미지의 intensity가 작은 부분과 큰 부분에서는 값의 변화를 적게주지만, intensity가 중간 부분인 회색으로 나타나는 부분은 constrast를 크게 만들어 디테일을 더욱 살리게 이미지를 만들 수가 있다.

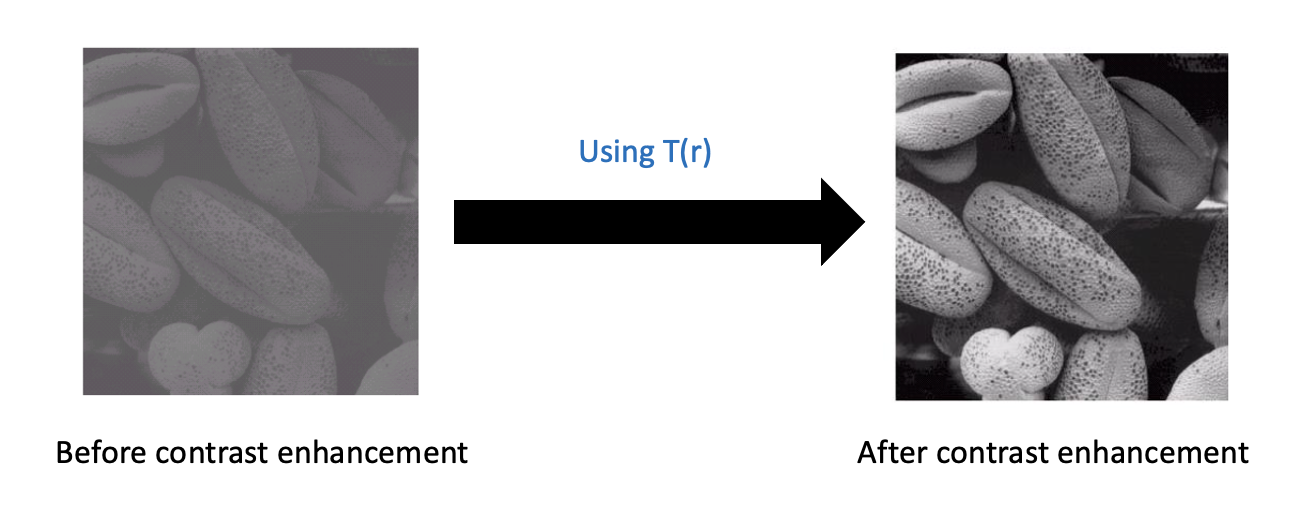임의로 만든 T(r)이라는 function을 이용해서 constrast를 high하게 만들어 이미지를 더욱 디테일하게 만들었다.