[계산사진학] Image Restoration - Image Denoising

JAEYOON SIM·2021년 11월 24일

Computational Photography

목록 보기

28/34

Classical Image Denoising

지금부터는 deep learning 이전 시대의 image restoration 기법들에 대해서 알아보고자 한다. 실제로 image restoration 기법은 정말 다양하게 존재한다. 앞으로 대표적인 3개의 image restoration 기법에 대해서 알아볼 것이다. Image denoising, super-resolution, deblurring이 3가지 기법이고, 대부분의 사람들이 흥미를 가지는 내용들이다. 그 중 첫번째로 image denoising을 알아볼 것이다.

Bilateral Filtering

Image denoising의 목표는 input image로부터 noise를 제거하는 것이다. Image denoising은 오랜 기간동안 연구되어온 분야이고, 다양한 approach들이 존재한다. Filtering 기반도 있고, inverse problem 기반도 있다. 첫번째로 filetering 기반의 approach에 대해서 알아볼 것이다.
Bilateral filtering은 filtering 기반의 approach로 noise를 제거할 수 있다.

Denoising

Bilateral filtering을 이용하면 noise를 제거하면서 edge를 보존할 수 있다.

Constrast Enhancement

Bilateral filtering은 다른 task에도 자주 사용된다.

Photo Retouching

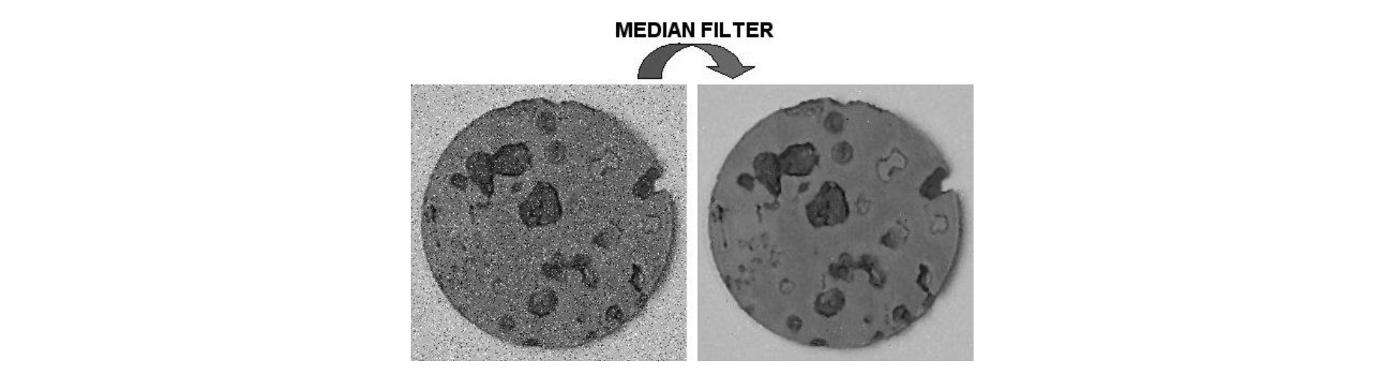
Median Filter

Median filtering의 경우 특히 salt-and-pepper noise를 제거하는데 효과적으로 사용된다.

Non-Local Means Filter

또 다른 유명한 filtering으로 non-local means filtering이 있다. 이 filter는 bilateral filter와 비슷하지만 더 강력하게 사용될 수 있다. 이 filter는 널리 사용되어 왔고, 요즘은 deep learning 기반이 더 성능이 좋아졌다. 그래도 deep learning 이전에는 가장 성능이 좋아서 널리 사용된 filter이다. 이제 이 filter가 어떻게 동작하는지 살펴보도록 하자. 다음과 같은 image가 있다고 해보자.
Non-local means filter는 bilater filter와 매우 비슷하기 때문에 먼저 bilateral filter에 대해서 간단하게 설명하고 이와 비교하면서 non-local means filter에 대해서 보도록 할 것이다. Image 상에서 target pixel의 noise를 없애기 위해서 주변의 pixel들을 search하고 target pixel과 intensity 값이 비슷한 pixel을 찾는다. Pixel 값이 비슷하다면 평균을 구해준다. 이러한 식으로 bilateral filter는 동작한다. 그러나 bilateral filter에서는 오로지 pixel 값만을 신경쓰고, 이는 문제를 발생시킨다. Pixel 값만을 비교하기 때문에 image의 위치적인 요소는 고려하지 못한다. 만약 target pixel에 대해서 유사한 값을 가진다고 하는 2개의 pixel이 완전히 다른 구역에 존재하는 경우에 대해서 문제가 생긴다. Noise가 없어도 이 2개의 값은 비슷해야한다. 만약 배경에 있는 pixel과 모자에 있는 pixel이 값이 비슷하다고 하면 이는 단지 우연의 일치이다. Noise가 없는 pixel 값은 다를 수 있다. 그래서 noise가 있는 상태에서 pixel 값이 비슷하다는 것은 우연일 가능성이 크다. 이러한 상황에서 평균을 구하는 것은 부정확한 결과를 만들어내게 된다. 이러한 상황이 bilateral filter를 사용했을 때 생기는 문제점이다.

그래서 non-local means filter는 이러한 문제를 해결해보고자 제안되었다. Non-local means filter는 단순히 다른 위치의 pixel에 대해서 pixel 값만 살피는 것이 아니라 patch를 사용하게 된다. 위의 예시에서 target pixel $p$ 가 있다고 했을 때, 주변 pixel 값만 보는 것이 아니고 patch까지 살펴볼 것이다. 만약 $p$ 주변의 $q1$ 이라는 지점의 pixel을 봤을 때, 값이 비슷하다면 해당 pixel 주변까지해서 patch로 잘라낼 것이다. 그리고 patch 사이의 거리를 계산할 것이다. 만약 patch가 서로 비슷해보인다면, pixel 값의 평균을 $p$ 와 $q1$ 에서 함께 계산해서 $p$ 의 noise를 제거할 것이다. 또한 $q2$ 를 대상으로도 patch 사이의 거리가 작다면 평균을 함께 계산할 것이다. 반면, $q3$ 라는 지점의 pixel을 보면 pixel 값은 비슷할 수 있어도 patch를 비교했을 때 다르다고 판단이 되면 사용하지 않을 것이다. 즉, pixel 값 자체를 보기보다 주변의 지역까지 patch로 사용해서 비교하자는 것이다. 그래서 non-local means filter는 다음과 같은 하나의 식을 이용해서 weighted average를 계산할 것이다.

y_i=\sum_{j\in{N(i)}}\text{exp }\bigg(-\frac{\|p_i-p_j\|^2}{h^2}\bigg)x_j

$x$ 는 input noisy image, $j$ 는 pixel index, $y$ 는 output, $p_i$ 는 $i$ 번째 $x$ 에서의 centered pixel의 patch이다. 그래서 non-local means filter는 patch 사이의 거리를 통해서 weighted average를 계산하게 된다. Non-local means filter는 patch를 사용해서 2개의 pixel이 서로 같은 구역에 있는지 판단할 수 있다. 그래서 이 filter는 bilateral filter보다 성능이 뛰어나다. 이 아이디어가 image denoising에서 좋은 결과를 가져왔다.

Non-local means filter를 사용하면 smooth하면서 디테일이 살아있는 결과를 만들 수 있다.

Denoising in the Transform Domain

Classical image denoising의 또 다른 방법으로는 denoising in the transform domain이다. 아이디어는 매우 간단하다. 우리는 Fourier transform이나 wavelet transform 등을 이용해서 image를 서로 다른 frequency component로 분해할 수 있다. Gaussian filter나 bilateral filter가 noise를 제거할 때 사용할 수 있다는 것을 알고있다. 그 이유가 대부분의 noise는 high frequency component이기 때문이다.

만약 image가 가공하지않고 기본 상태의 자연스러운 image라면 low frequency에서 더 크고 강한 signal을 가지게 될 것이다. High frequency component의 크기는 상대적으로 작다. 만약 noise가 모든 frequency에 균일하게 분포하고 있다면 high frequency compontnent signal의 크기는 noise의 크기보다 상대적으로 작을 것이다. 그래서 high frequency component에서 noise가 더 두드러지는 것이다. 그래서 noise를 제거하는 방법으로 서로 다른 frequency component로 분해해서 오로직 high frequency component에서의 noise만 신경쓰는 것이다. 이러한 이유때문에 Gaussian filter와 bilateral filter를 image denoising에 사용한다.

더 직접적인 방법으로 이 아이디어를 기반으로 image transformation을 이용해서 image를 frequency component에 따라 분해할 수 있다. 예를 들어, wavelet transform을 이용해서 high frequency component를 제거하는 것이다. 위의 image는 wavelet transform의 결과를 나타낸 것이다. 그래서 high frequency component에 해당하는 image에서 특정 threshold보다 크기가 작은 high frequency component를 제거하는 것이다. 여기서 기본적인 가정으로 high frequency component에서의 작은 변동이 대부분 noise 때문이어야 한다. 그리고 제거를 한 뒤에는 inverse transform을 적용한다. 그러면 우리는 noise가 없는 image로 복원할 수 있다.

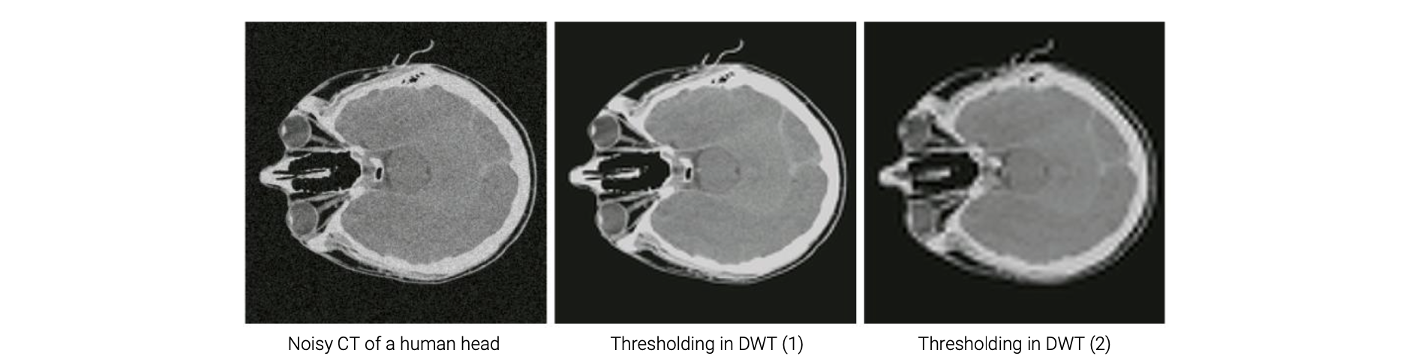CT image를 보면 noise가 많이 존재한다. 이 image에 discrete wavelet transform을 적용해서 thresholding을 통해서 noise를 제거해주고, image를 다시 복원해주면 noise가 사라진 결과를 얻을 수 있다. 결과를 보면 noise가 대부분 사라진 것을 볼 수 있다. 그래서 이 방법은 꽤 직관적이고 효율적이다.

BM3D

지금까지 non-local means filtering과 transform 기반의 image denoising에 대해서 알아보았다. 그렇다면 만약 이 2개의 아이디어를 합치면 어떻게 될까? 그래서 등장한 것이 BM3D이다.
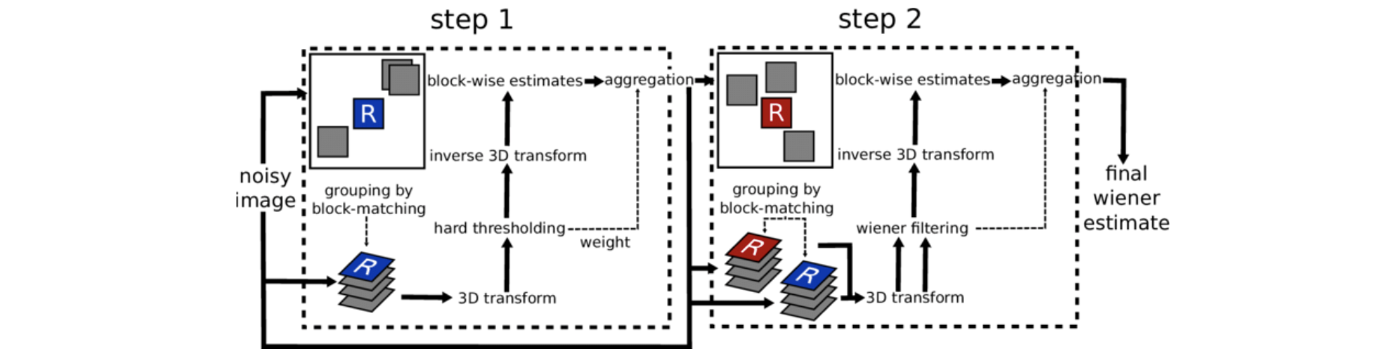BM3D는 non-local means filtering과 transform 기반의 image denoising 기법을 합친 것이다. 이 방법은 13년도 더 이전의 방법이지만 굉장히 효율적인 방법이라 널리 사용되고있다. BM3D는 block matching이라는 것을 사용한다. 위의 diagram은 BM3D가 동작하는 방법을 보여주고 있다. BM3D의 주된 아이디어는 block matching과 3D transform을 사용한다는 것이다. Block matching은 사실상 non-local means filtering에 대응되는 방식이다. 3D transform과 hard thresholding은 transform domain 상에서의 low pass filtering에 해당한다. 이러한 방식을 이용해서 고성능을 기록했다.

Denoising as an Inverse Problem

Image denoising에 대해서 다른 approach도 있다. 주목해 볼 방법으로는 image denoising problem을 inverse problem으로서 접근하는 것이다. 가장 먼저 해야할 일은 어떻게 image를 degrading하는지 가정하는 것이다. 예를 들어서 noise가 없는 image를 평균이 0인 additive Gaussian noise에 의해서 degrading 된 것으로 볼 수 있다. 이러한 가정을 기반으로 image degradation model을 수식화 할 수 있다.

y=x+n

n \sim N(0,\sigma^2)

$x$ 는 noise가 없는 image이고 $y$ 는 noisy image, $n$ 은 additive noise이다. 이러한 식으로 간단하게 image degradation model을 정의할 수 있고, 이를 기반으로 image denoising을 inverse problem으로 수식화 할 수 있다.

f(x) = \|x-y\|^2 + p(x)

p(x)\text{ : regularization or prior}

우리는 noise generation process를 뒤짚고 싶다. 그래서 위와 같이 energy function을 얻을 수 있다. 그리고 우리는 objective function을 최소로 만드는 $x$ 를 찾을 수 있다. 효율적인 image denoising을 위해서 중요한 것은 regularization term이다. 어떻게 이 prior term이 image denoising에서 마지막으로 충분한 성능을 내도록 디자인 되는 것일까? Image denoising을 inverse problem으로 다룰 때 가장 중요한 부분은 이 prior term이다. 지금까지 여러 연구들이 이 image prior를 중점적으로 연구가 되어졌다. 좋은 prior는 좋은 퀄리티의 결과를 얻는데 있어서 필수적인 것이다. Prior term은 복잡해보이지만 이를 포함한 결과는 충분히 훌륭하다.

Denoising with DNNs

DnCNN

이번에는 imag restoration에서 deep learning 기반의 방식들을 알아볼 것이다. Deep learning based approach는 dominant approach이다. 왜냐하면 deep learning 기반의 모든 방식이 기존의 classical based method보다 모두 성능이 뛰어나기 때문이다. 그래서 최근의 image restroation 문제들은 모두 deep learning을 사용해서 해결하곤 한다. Deep learning에는 3개의 중요한 factor들이 존재한다. Neural network architecture, how to train, 그리고 training data가 중요한 factor들이다. 특정 문제를 해결하고자 deep learning을 사용하고자 할 때는 이 3가지 factor들을 항상 생각해야 한다. 이 3가지를 중점적으로 생각하면서 먼저 image denoising을 볼 것이다.

Image denoising에서 가장 대표적인 deep learning method는 바로 DnCNN이다. DnCNN은 2017년도에 "Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising"이라는 논문에서 제안된 방식이다. 이 논문에서 다음과 같은 network architecture를 제시했다.

이 architecture는 매우 간단하다. 단순히 여러개의 convolution layer와 ReLU function으로 이루어져 있다. 그래서 딱히 특별하게 살펴볼 특징은 없다. 이 논문에서는 이러한 간단한 구조의 architecture로도 image denoising 문제를 해결할 수 있다고 한다.
그리고 추가적으로 resiual learning이라는 것을 제안했다. Image denosing은 noise가 있는 image가 먼저 필요하다. 이러한 noisy image를 위의 간단한 neural architecture에 집어 넣었을 경우 우리가 원하는 결과는 noise-free image이다. 하지만 이러한 결과 대신에 이 논문에서는 neural architecture의 결과로 residual image를 예측하도록 했다. Residual image는 일종의 noise map이고, 이 논문에서 clear image를 $x$ 라고 했을 때 noisy image를 $y=x+n$ 이라고 정했다. 그러면 이러한 neural network를 사용해서 noise $n$ 을 예측하도록 했다. 그러면 이러한 noise $n$ 을 input image $y$ 에서 빼주면 clear image $x$ 를 예측할 수 있다는 것이다. 이렇게 진행하는 것이 residual learning의 아이디어이다. 최종적으로 noise-free image를 얻기 위해서 바로 noise-free image를 예측하기보다는 input에서 뺄 수 있는 noise map을 예측했다. 이 논문에서 이야기하는 바로는 이렇게 residual image를 예측하는 것이 noise-free image를 예측하는 것보다 더 효과적임을 밝혀냈다.

이러한 방법이 무조건적으로 옳다는 것은 아니지만, neural network가 0에 가까운 값을 예측하는데는 더 효과적이라고 말했다. 예를 들어서 input image의 pixel 하나를 예측한다고 해보자. 대부분의 pixel 값들은 0으로부터 멀리 떨어져 있을 것이다. 만약 밝은 부분의 pixel을 본다면 그 값은 0으로부터 더 멀리 떨어져있을 것이다. 그래서 이러한 값일수록 neural network를 사용해서 예측하는 것은 더 어려울 것이다. Noise map은 대부분의 값이 0에 가까이 존재하고, 0-mean noise를 가정하면 이러한 noise의 평균은 0이 된다. 특정 pixel 값을 예측하고자 할 때 모든 noise component가 0에 가까워서 neural network로 학습시키는 것이 더 쉬울 것이다. 이러한 이유들로 인해서 residual learning을 사용하는 것이다. 특히 residual learning은 다른 image restoration에서도 효과적으로 사용이 된다.

지금까지는 첫번째 factor인 neural network architecture에 대해서 살펴보았고, 지금부터는 두번째 factor인 how to train에 대해서 살펴보고자 한다. Image restoration task에서 ㅣoss function은 매우 간단하다. 일반적으로 많이 사용하는 training scheme은 mean-squared-error(MSL) loss를 사용해서 학습시키는 것이다.

L = \sum_i\|(x_i-f(x_i;\theta))-y_i\|^2

$f$ 는 neural network, $\theta$ 는 network parameter, $x_i$ 는 noisy image이다. 앞서 DnCNN이 noise map을 예측하는 것이라고 했기에 clear image를 얻기 위해서는 noisy image $x_i$ 에서 neural network의 output $f(x_i;\theta)$ 을 뺴줘야 한다. 이렇게 뺄셈 연산을 해주면 denoising image를 얻게 되고, 우리가 원하는 것은 이러한 예측 결과와 ground truth가 비슷하기를 원한다. 그래서 model에 의해서 예측된 결과와 ground truth를 뺄셈 연산을 해줘서 그 결과를 최소로 만들어야 한다. 그래서 우리는 이러한 difference를 이용해서 만든 loss function $L$ 을 최소로 만드는 model parameter $\theta$ 를 찾아야 한다. 물론 이외에도 loss function은 많이 존재하지만, 이렇게 정의하는 것이 가장 일반적이고 전통적인 방식이다.

이러한 방식으로 학습을 진행시키고자 할 때, noisy image $x_i$ 와 noise-free image $y_i$ 를 쌍으로 가지고 있어야 한다. 이러한 $(x_i,y_i)$ 를 training data로 가지고 있어야 한다. 이렇게 network를 학습시키게 되면은 다음과 같이 denoising result를 얻을 수 있다.
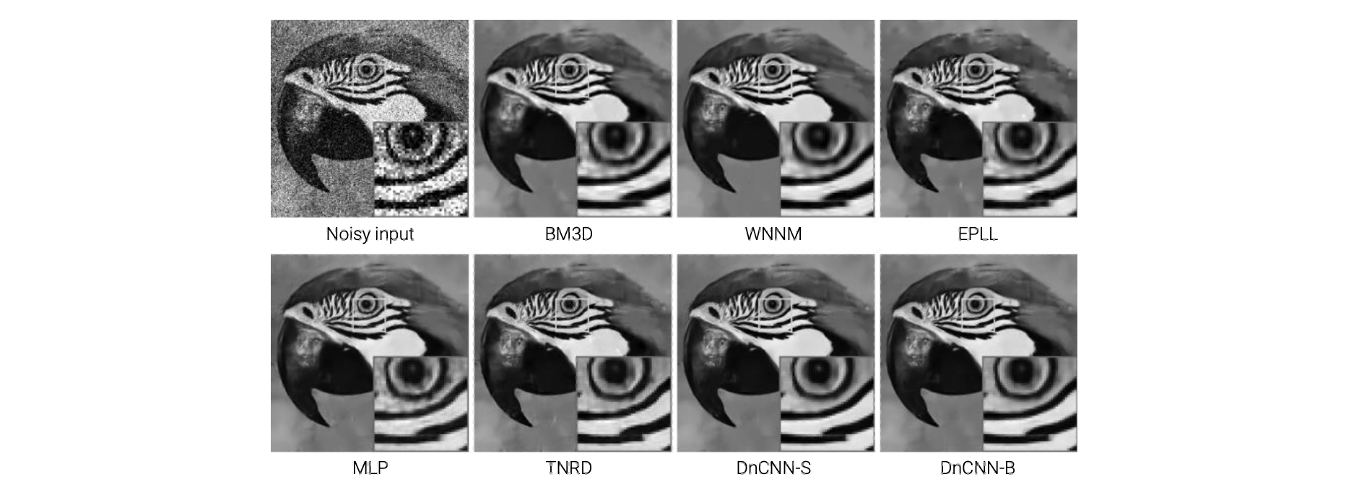Classical approach인 BM3D의 deep learning 이전에 성능이 가장 좋고, deep learning approach 인 DnCNN도 결과가 잘 나오는 것을 볼 수 있다. EPLL은 매우 복잡한 prior를 사용해서 inverse problem을 푼 것이다. 결론적으로 neural network를 학습시키는 것이 더 효과적으로 image denoising 결과를 만들 수 있다.

Classical approach인 BM3D와 EPLL은 computational time이 매우 길었고, 그럼에도 불구하고 결과는 그리 좋지 못했다. 반면 DnCNN같은 경우 학습 시간이 길긴 하지만 검증 시간은 매우 빨랐고, 그 결과도 매우 우수했다.

NLRN

Image denoising은 다음과 같이 2가지 기법으로 나눌 수가 있다.

External database-based method: Input으로 많은 양의 training data가 있다고 했을 때, 이를 이용해서 noise가 없는 clean image의 특징들을 학습시킬 수 있다. 이 방법은 일반적으로 많이 사용되는 deep learning 기법이다. 흔히 deep learning은 external training data를 사용해서 최적의 network parameter를 찾는다. 여기서 input에 이미 존재하는 정보를 사용하는 것이 아니다.
Self-exemplar based method: Input에 이미 정보가 포함되어 있는 경우이다. Noise를 없애기 위해서 input image에 이미 존재하는 정보들을 사용할 것이고, 특히 해당 pixel의 noise를 없앤다고 했을 때 주변의 정보들을 활용하게 된다. 왜냐하면 pixel간 거리가 가까울수록 비슷하다는 가정 아래 같은 질감이나 색상의 정보를 사용하려는 것이다. 이러한 아이디어는 non-local means filtering의 기반이 되고, 특히 input image에 반복적인 패턴이 잘 보이는 경우에 한에서 external database-based method보다 더 효과적이게 된다.

Image denoising은 계속해서 연구가 활발히 되는 분야로 이번에 볼 논문은 2018년도에 제안된 "Non-Local Recurrent Network for Image Restoration"이다.
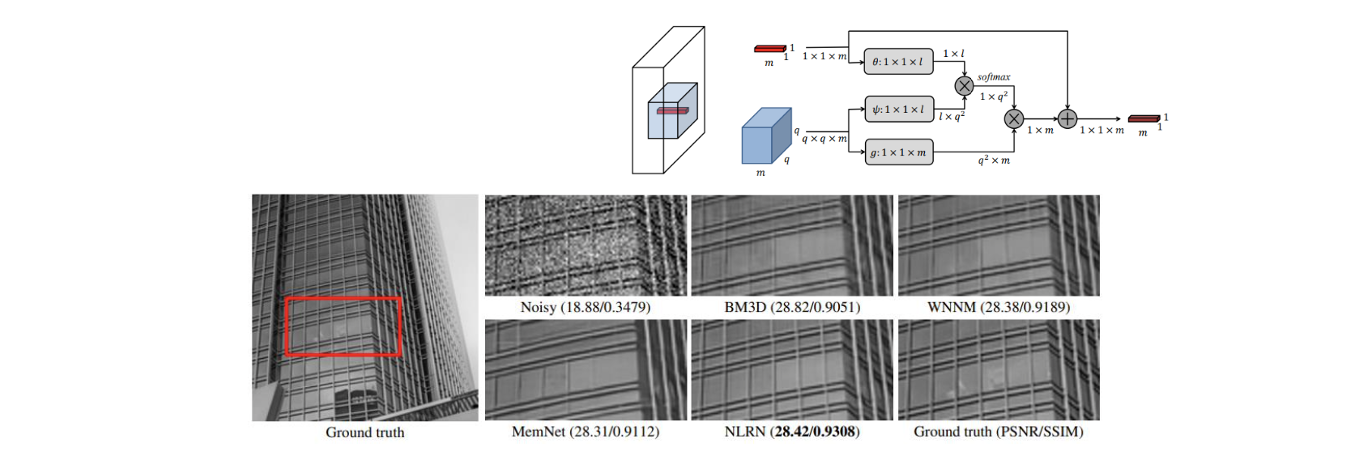이 논문에서는 input image의 반복되는 패턴을 추출하기 위한 neural network-based approach를 소개하고 있다. Noisy image를 보면 일정한 패턴이 반복되는 것을 볼 수 있다. 특정 pixel의 noise를 제거하고자 할 때 이웃한 다른 pixel을 이용하게 된다. 그래서 이 논문에서는 neural network 버전의 non-local means filtering을 진행했다. Noisy image를 input으로 사용하고 neural network를 통과시켜서 feature map을 계산했다. 각 feature는 noisy image에 patch에 대응이 되는데, 이는 receptive field 때문이다. 기본적으로 feature map은 noisy image에서 local image patch에 대응되고, patch의 크기는 receptive field의 크기에 대응된다. 그리고 우리는 feature map을 사용해서 non-local means filtering을 수행할 수 있다.

특정 feature을 denoise하고자 한다면 neural network에서 feature volume을 얻어낼 수 있다. 그러면 이 feature volume에서 이웃하는 pixel들의 feature를 가지게 되어서 similarity를 계산할 수 있다. 위에서 빨간 feature의 noise를 없애고자 할 때 파란 feature volume을 이용해서 빨간 feature와 파란 feature volume에 포함되어 있는 다른 feature 사이의 simiarity를 구하고자 하는 것이다. 그러면 구해진 similarity를 기반으로 우리는 빨간 feature의 weighted average를 계산할 수 있다. 그래서 결과적으로 denoised feature를 얻을 수 있고, 이는 feature volume에 있는 feature의 weighted average result이다.

이렇게 구해진 denoised feature map을 다른 neural network에서 사용해서 image를 복원할 수 있고, 이렇게 복원된 image는 denoising result가 된다. 기본적으로 이 neural network는 image denoising approach의 양쪽 모두에서 이득을 낼 수 있다. 그리고 neural network는 여전히 학습이 가능한 parameter를 가지고 있어서 external database로부터 최적의 parameter를 학습해서 denoising의 퀄리티를 개선시킬 수 있다. 동시에 이러한 network architecture를 사용하면 input image에서 self-exemplar를 얻어낼 수 있다. 양쪽으로부터 이득을 얻게되면 성능이 좋아지게 되고, 이것이 non-local recurrent network의 결과였던 것이다. 예시로부터 반복되는 패턴일수록 복원 결과가 좋아진다는 것을 알았다.

Denoising Datasets

Image denoising을 위한 neural network를 학습시키기 위해서는 noise-free image와 noisy image 쌍이 필요하다. 예를 들어 image denoising을 위한 neural network가 있다고 해보자. 이 neural network는 input으로 noisy image를 사용해서 denoising result를 만들어 낸다. 그래서 이러한 network의 학습을 위해서 ground truth로 noise-free image가 필요하다. Loss term은 denoising result와 ground truth denoising image를 이용해서 mean squared error와 같은 방법을 통해서 정의할 수 있다. 우리는 이 loss를 줄이기 위해서 neural network를 학습시킬 수 있다.

Synthetic Datasets

그래서 핵심은 network 학습을 위해서 noisy image와 ground truth noise-free image가 필요하다는 것이다. 다음의 2개의 image는 같은 내용물을 가지고 있어야 한다. 모든 것이 비슷해야하고 오직 noise의 차이만이 존재해야 한다.
그러나 사실 위와 같은 image 패턴을 구하는 것은 어렵다. 같은 대상에 대해서 noise가 없는 것과 noise가 있는 결과를 얻어내야 한다. 그리고 장면과 풍경 모두 정확히 일치해야 한다. 그래서 이러한 image를 얻는 것은 상당히 어렵고, 얻기 위해서 상당히 많은 시간이 소모될지도 모른다. 기술적으로 이러한 noisy image를 찍는 것이 상당히 어렵기 때문이다.

그래서 이전의 image denoising method는 대부분 합성해서 만들어진 synthetic dataset을 사용했다. Synthetic dataset을 만드는 가장 간단한 접근법은 먼저 여러개의 sharp noise-free image에다가 random Gaussian noise를 더하는 것이다. 여기서 Gaussian noise를 가정하게 되면 normal distribution으로부터 pixel-wise noise를 sampling 할 수 있다. 여기서 random number generator를 사용하기 때문에 sampling은 꽤 간단하다. Synthetic dataset를 만드는 이러한 과정은 많은 image denoising을 위해서 여태껏 널리 사용되어져 왔다. 그러나 이렇게 합성해서 만든 image는 비현실적이라는 문제가 존재한다. Noise 패턴이 사실상 현실 세계에서의 noise와 비슷하지 않다. 그래서 합성된 data들만으로 학습이 된 network는 현실 세계의 image에 대해서는 제대로 동작하지 않는다.

Darmstadt Noise Dataset(DND)

현실 세계에서의 image denoising dataset을 모으는 작업들도 많이 진행되어 왔다. DND dataset으로 불리는 Darmstadt Noise Dataset은 "Benchmarking Denoising Algorithms with Real Photographs"라는 논문에서 2017년도에 소개되었다.
이 dataset은 50 쌍의 고해상도 image와 해당 realistic noisy image 를 가지고 있다. 즉, ground truth sharp imaged와 noisy image를 쌍으로 학습시키기 위해서 dataset이 만들어졌다. 좌측이 noise-free image, 우측이 noisy image이다. 두 image모두 카메라에 의해서 촬영된 image이고, 촬영하는 과정에서 생긴 noise를 가지고 있다. 이 dataset을 모으기 위해서 총 4대의 카메라를 사용했고, data를 얻을 때는 굉장히 조심스러운 환경에서 진행이 되었다. 통제가 가능한 환경에서 삼각대와 같은 보조 장비를 사용해서 같은 장면을 두번씩 촬영했다. Noise-free image를 얻기 위해서 ISO를 조절해야 하는데, 만약 ISO 값을 낮출수록 noise는 그만큼 줄어들게 된다. 단순히 ISO 값의 조절로는 완전히 noise를 없앨 수 없기 때문에 촬영 과정에서 좀 더 복잡한 과정을 통해서 noise를 조절했다. 그리고 50 쌍만 존재하기 때문에 단순히 학습용으로 소개된 것은 아니다.

저자는 이 dataset을 이용해서 다양한 실험을 진행했고, 실험을 통해서 deep learning 기반의 image denoising보다 classical approach가 성능이 좋게 나온다는 것을 발견했다. 당시 deep learning은 합성된 image들을 이용해서 학습을 진행했기 때문이다. 그래서 저자는 이를 통해서 dataset의 중요성에 대해서 말하고자 했다.

SIDD

또 다른 현실 세계의 image denoising dataset으로는 SIDD가 있다. 이 dataset은 "Smartphone Image Denoising Dataset"이라는 논문에 2018년도에 소개되었다. 이 dataset은 이전보다 많은 data 쌍을 모으려고 했으며, 총 320 쌍의 data를 이용해서 neural network를 학습시키려 했다.
이 논문에서는 적절한 dataset을 사용해서 학습을 시키면 image denoising 성능을 올릴 수 있다고 말했다.

JAEYOON SIM

평범한 공대생의 일상 (글을 잘 못 쓰는 사람이라 열심히 쓰려고 노력 중입니다^^)