[계산사진학] Image Warping 2

Recovering Transformations

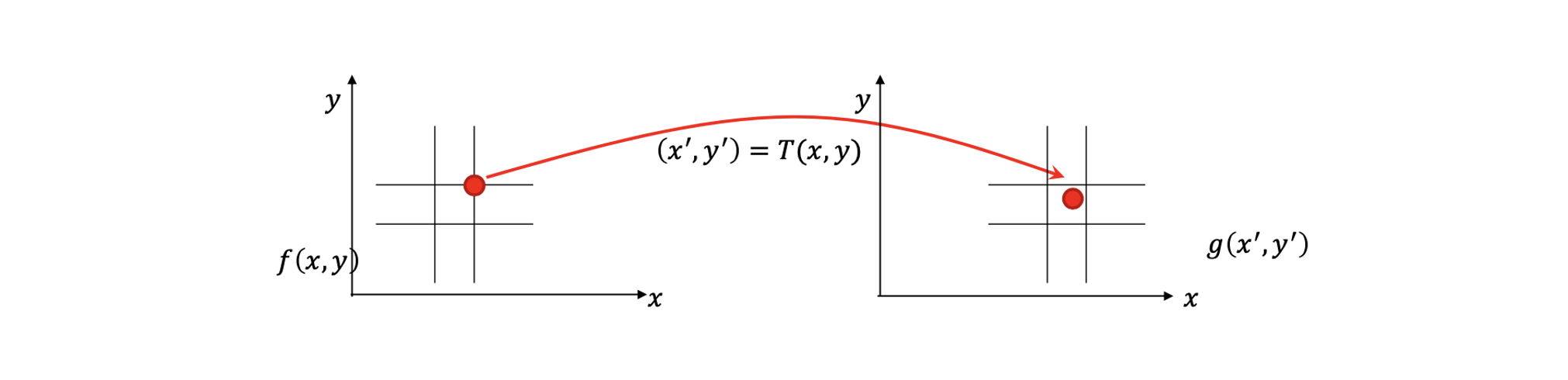
이전에는 서로 다른 transformation들에 대해서 다루어보았다. 만약 2개의 image를 가지고 있다면 이들 사이의 적절한 transformation을 어떻게 찾을 수 있을까?
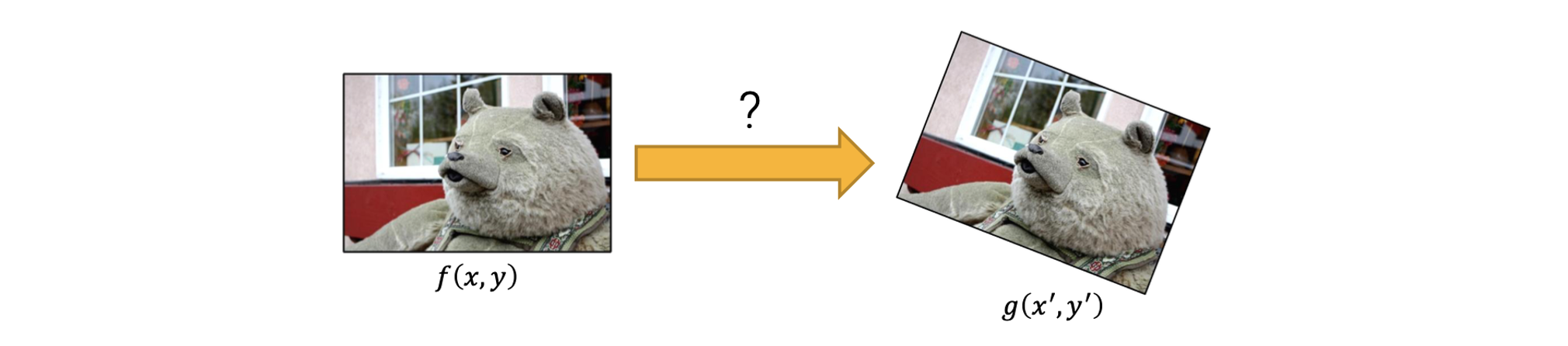이번에는 transformation을 찾는 방법에 초점을 맞출 것이다. 위와 같이 2개의 이미지 $f, g$ 가 있고, $g$ 는 $f$의 warped 결과가 될 것이다. 이때 우리는 어떻게 이들 사이의 transformation을 찾을 수가 있을까?

Recovering Translation

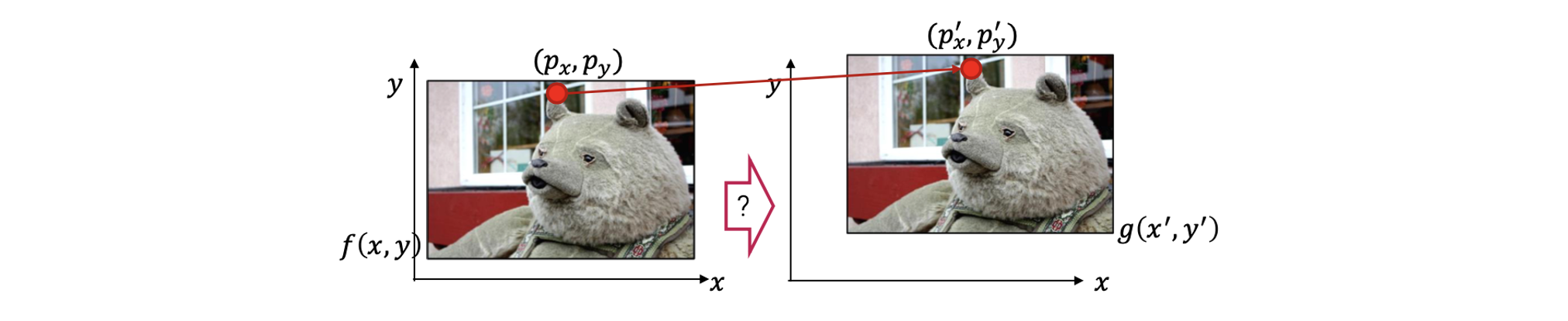만약 transformation이 translation이라면, 2개의 image로 $f$ 와 $g$ 사이의 한 점에 대한 correspondence로부터 얼만큼 이동했는지 찾을 수 있을 것이다. 즉, 우리는 translation parameter들을 찾을 수 있게 된다.

Recovering Similarity

만약 transformation이 similarity라면, 우리는 2개의 점에 대한 correspondence가 필요해진다. 2개의 correspondence에 대해서 우리는 얼마나 이미지가 이동했는지(translation), 얼마나 회전했는지(rotation), 그리고 uniform scaling factor를 찾을 수 있다.

예를 들어 우리는 2개의 correspondence로부터 mean vector를 계산할 수 있을 것이다. 이때 mean vector로부터 우리는 translation parameter를 찾을 수 있다. 그리고 2개의 image로부터 2개의 점들과 수직방향으로의 각도를 구할 수 있다. 그래서 이 2개의 각도를 이용해서 rotation angle을 구할 수 있게 된다. 마지막으로 2개의 image로부터 다시 2개의 점들을 잇는 선의 길이를 구해서 비교한 뒤에 uniform scaling factor를 찾을 수 있다. 그래서 similarity transformation을 찾기 위해서는 2개의 corespondence를 필요하게 된다.

Similarity transformation은 총 4개의 degrees of freedom(DoF)를 가지게 되는데, 이는 총 4개의 parameter 혹은 unknown을 필요로 한다는 것이다. 위에서 각각의 correspondence는 빨간선으로 표시되어 있고, 각각 x좌표와 y좌표에 대응되는 2개의 식을 제공해서 총 4개의 식을 얻을 수 있다. 그래서 4개의 점으로부터 2개의 correspondence를 얻을 수 있고, 이로부터 각각 2개의 식이 도출되어 총 4개의 식으로부터 4개의 parameter를 구하면 된다. Parameter 하나는 $s$ 로, 또 다른 하나는 $R$ 로, 그리고 마지막 2개는 $t$ 로 사용이 될 것이다.

Recovering Affine

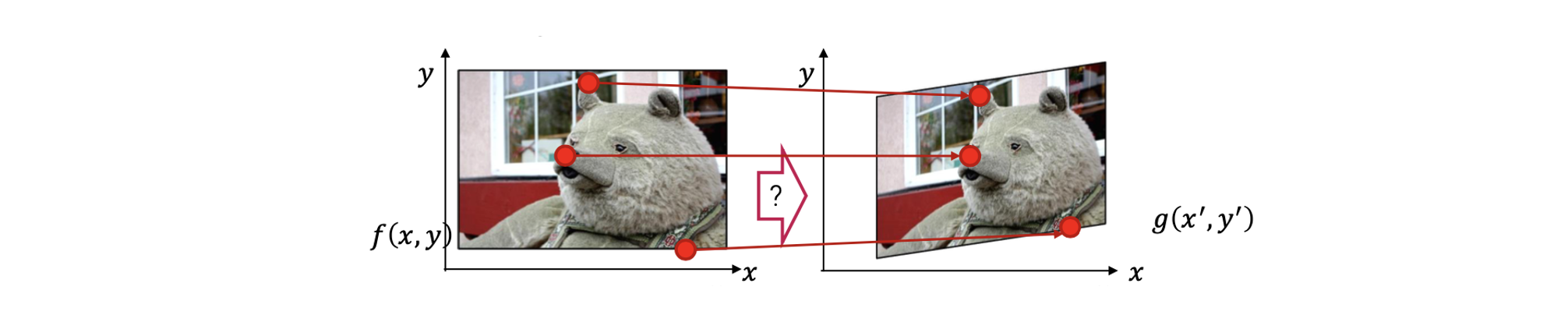만약 transformation이 affine이라면, 우리는 3개의 점에 대한 correspondence가 필요해진다. 우리는 이미 affine transformation이 6 DoF를 가져서 6개의 parameter가 필요하다는 것을 알고있다. 그래서 결과적으로 총 3개의 correspondence가 필요하고, 이로부터 6개의 parameter를 구할 수 있다.

Recovering Projective

만약 transformation이 projective라면, 우리는 총 4개의 점에 대한 correspondence가 필요해진다. 그래서 결과적으로 총 4개의 correspondence가 필요하고, 이로부터 8개의 parameter를 구할 수 있다.

Projective transformation은 평면으로부터 가장 일반적인 warping을 설명한다. 그래서 어떠한 사각형이 있을 때, 이 사각형이 찌그러진 모양의 사각형으로 mapping이 된다. 이러한 경우에 일반적으로 4개의 꼭지점으로부터 4개의 correspondence를 이용한다.

Forward/Inverse Warping

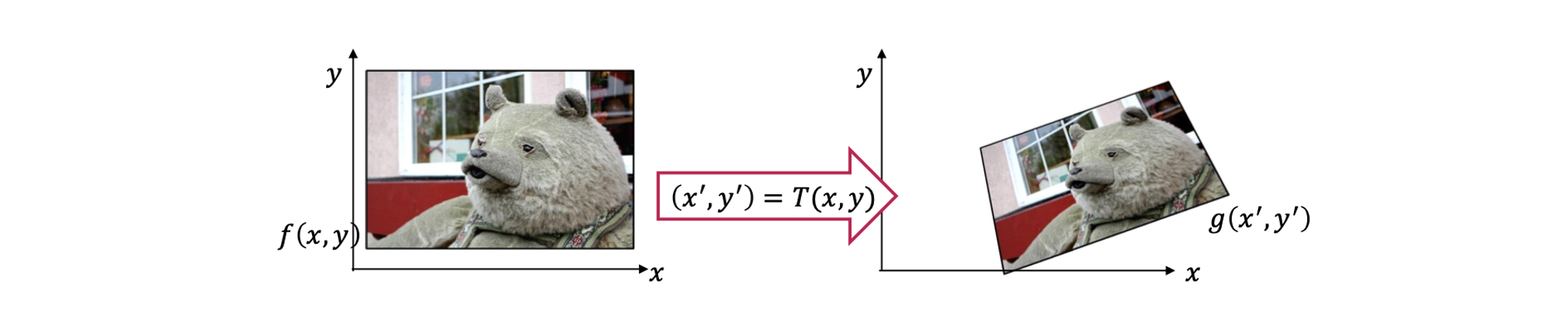
Source image $f$ 와 transformation $T$ 를 이미 알고 있다고 해보자. 그러면 실제로 어떻게 image를 warping 할 수 있을까? 즉, 어떻게하면 transformed image $g$ 를 계산해서 구할 수 있을까?

Forward Warping

일반적으로 2개의 다른 접근 방식이 존재한다. 첫번째가 바로 forward warping이다. Foward warping의 기본 아이디어는 $f$ 로부터 각각의 pixel을 target image에서 이와 대응되는 위치의 $(x',y') = T(x,y)$로 보내는 것이다.
그래서 source image로부터 각각의 pixel로부터 target image의 대응되는 지점으로 transformation $T$ 를 이용해서 보낼 수가 있다. 위치로 보낸 후에는 해당하는 위치의 값을 그대로 복사해서 붙여 넣어주면 된다.

이러한 접근 방법을 정말로 직관적으로 간단해 보인다. 그러나, 여기에는 몇가지 문제점들이 존재한다. 첫번째는 만약에 pixel이 2개의 pixel 사이로 보내지면 어떻게 될까? Transformation은 간단한 matrix 계산을 통해서 수행된다. 그래서 바뀐 위치가 무조건 정수로 떨어지지 않을 수가 있다. 그래서 1.5와 같은 실수는 일반적인 pixel 좌표에서는 사용할 수 없다. 그러면 이러한 문제를 어떻게 해결해야 하는 것일까?
간단하게 이웃하는 pixel들에게 값을 나눠줌으로써 문제를 해결할 수 있다. 다시 말해서 간단하게 bilinear interpolation과 같은 방법으로 blending 해주는 것이다.

사실 더 중요한 문제는 $T$ 가 image의 크기를 증가시킬 때다.
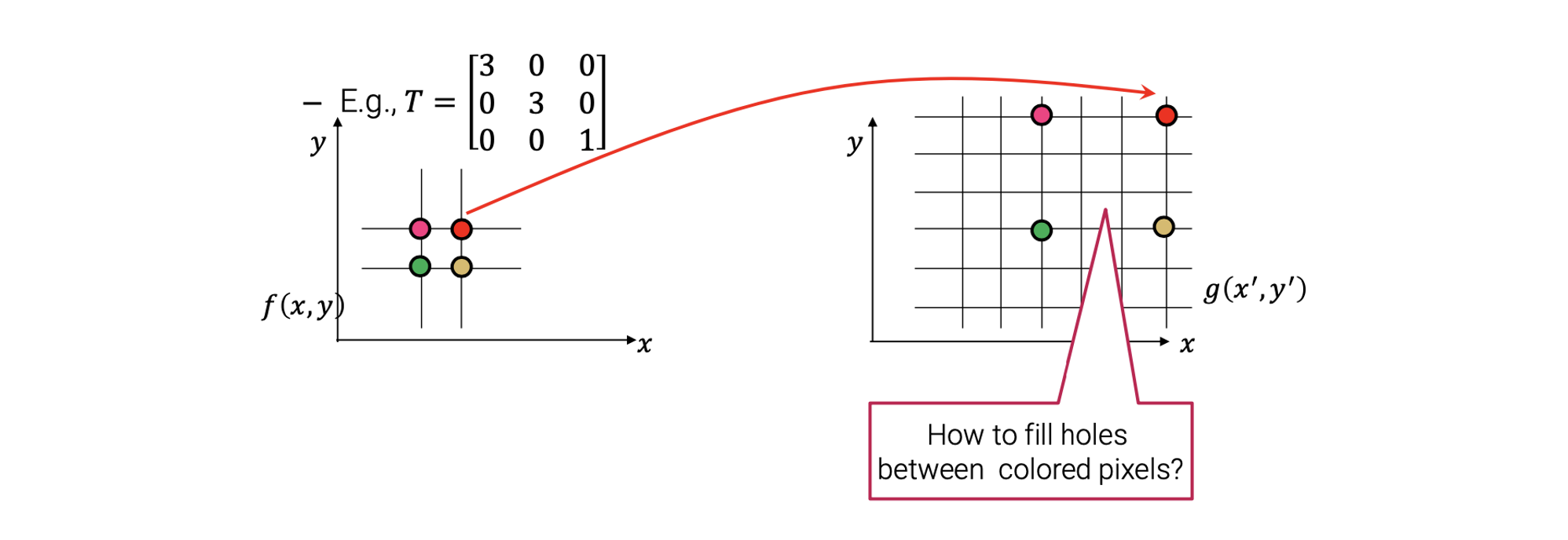예를 들어서 4개의 pixel의 traget image에 위와 같이 보낸다고 해보자. 그러면 이제 target image 상에 큰 구멍이 생기게 될텐데, 이를 어떻게 채워야 하는 것일까? 아무래도 구멍의 크기가 꽤 커서 단순한 방법으로는 해결하지 못할 것이다.

Inverse Warping

이러한 문제때문에 forward warping 대신에 inverse warping이 더 많이 사용되고 있다. Inverse warping에서 transformed image로부터 각각의 target pixel에 대해서 우리는 inverse transformation($T^{-1}$)을 이용해서 source image에 대응되는 pixel의 위치를 구할 수 있다.
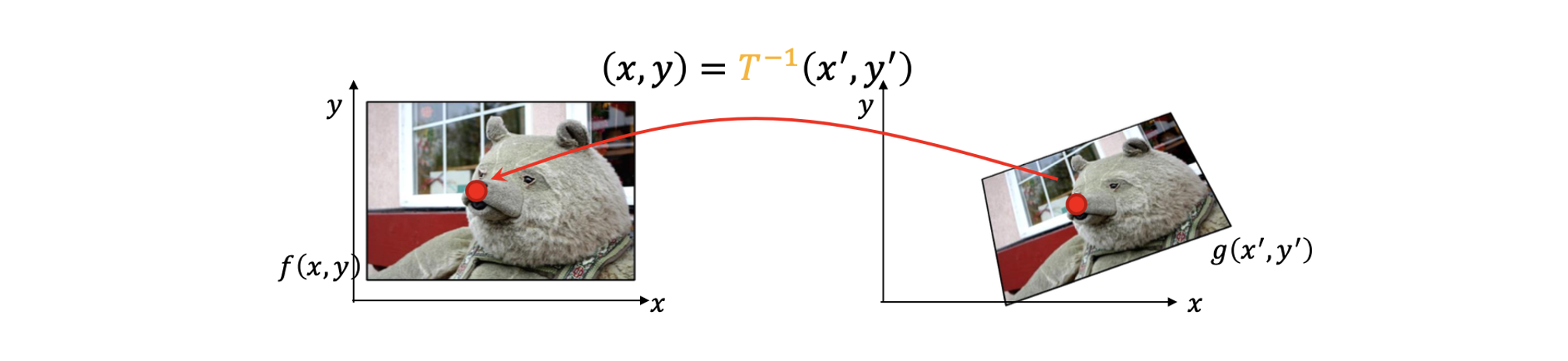위치를 구하고 나면 source pixel의 값을 복사해서 대응되는 target pixel의 위치에 붙여넣어 주는 것이다. 그러면 이제 어떻게 이러한 inverse warping이 문제를 해결하는지 보도록 할 것이다.

다시 문제를 정의해서 pixel들이 2개의 pixel 사이 어딘가로부터 도착하면 어떻게 해야할까?
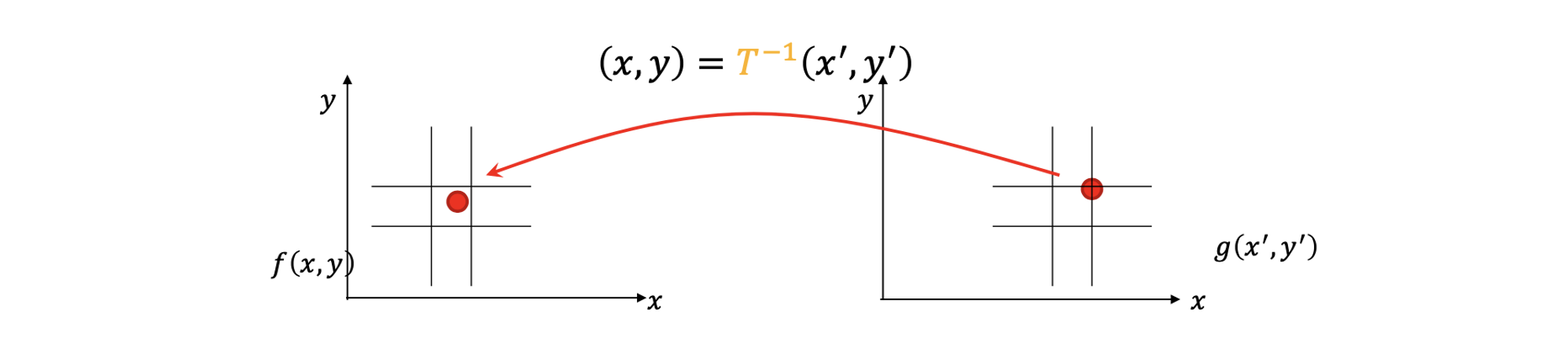그러면, 우리는 간단하게 color 값을 interpolation 할 수 있다. 만약 source pixel이 좌측과 같이 어딘가에 위치한다면, 간단하게 해당하는 pixel의 이웃들로부터 color 값을 interpolation을 통해서 구할 수 있다는 것이다. 그러면 이제 target 지점에 interpolation 결과로 얻은 값을 복사할 수 있다. 그래서 이 문제는 쉽게 해결 될 수 있다. 이러한 문제 외에도 더 중요하게 inverse warping은 심지어 transformation $T$ 가 scaling transformation이라도 구멍이 생기는 문제가 발생하지 않는다. 왜냐하면 모든 target pixel의 위치에 대해서 반복하기 때문이다. 그러면 각각의 target 지점으로 대응되는 source pixel의 값을 복사해서 보낼 수 있다. 그래서 우리는 구멍이 생기는 문제를 피할 수 있게 된다.

Forward vs. Inverse Warping

Forward warping과 inverse warping에서 어느것이 더 낫다고 할 수 있을까? 지금까지 봐왔듯이 inverse warping이 구멍을 없앨 수 있다는 측면에서 훨씬 더 좋은 선택이 된다. 그러나 이러한 접근은 warping function이 invertible해야한다는 조건이 필요하다. 운이 좋게도 지금까지 살펴본 transformation은 모두 쉽게 inverse를 구할 수 있다. 그러나 때때로 더 복잡한 warping function을 사용하게 되면, inverse warping을 사용하는 것이 불가능할지도 모른다. 그래서 이러한 경우에 우리는 forward warping을 사용해야 한다.

More Complicated Models

지금까지 parametric global transformation에 대해서 알아보았다. 그러나 때때로 정교한 warping model을 사용해야 한다. 이러한 복잡한 경우로는 mesh grid가 존재한다.
Mesh grid는 image를 여러개의 tile로 분해한다. 각각의 tile은 affine transform이나 homograph와 같이 간단한 warping function에 의해서 휘어지게 된다. 이러한 mesh grid를 이용하면 image는 자유롭게 모양이 변하게 된다.

다른 예시로는 optical flow가 있다.
Optical flow는 2D vector map으로 각각의 pixel은 자신의 2D motion vector를 가지게 된다. 이러한 optical flow는 비디오 프레임으로부터 motion을 설명하기 위해서 사용된다. 다른 부분이라면 다르게 움직일 것이다. 위의 예시에서 빨간 차는 뒤로 이동할 것이고 옆의 background는 앞으로 이동할 것이다. 그래서 모든 pixel이 자신만의 2D motion vector를 가지게 된다. 비록 모든 motion vector가 시각화 되지는 않았지만, 실제로는 모든 pixel 자신만의 motion vector를 가지고 있다.