[그래프 기계학습] Deep Graph Generative Models 1

Deep Generative Models

이번에 알아볼 deep graph generative model은 이전까지 알아보았던 graph representation learning과는 조금 다르다. Graph와 더불어 최근에는 굉장히 쉽게 고화질의 image와 괜찮은 text를 deep generative model로부터 만들 수가 있다. 대표적으로 ChatGPT는 우리가 물어보는 것에 대해서 굉장히 좋은 답변들을 제시해주고 있다. 예를들어 "An illustation of an avocado sitting in a therapist's chair, ..."과 같은 프롬프트를 입력했을 때 위와 같은 결과를 얻을 수가 있는 것이다. 또한, ChatGPT는 일반적인 답변 이외에도 유머러스하고 독창적인 답변들을 많이 제공해주기도 한다.

우리가 deep generative model로부터 얻을 수 있는 가장 중요한 부분은 우리가 ChatGPT와 같은 플랫폼에 science와 관련된 질문을 했을 때 믿을 수 있는 답변들을 제공받을 수 있다는 것이다. Science는 아무래도 현실 세계를 가장 잘 반영할 수 있는 영역이기에 이와 관련되어 신뢰할 수 있는 답변은 우리에게 굉장히 중요한 요소로 다가오게 된다. 가령, deep generative model을 기반으로 하는 ChatGPT와 같은 플랫폼은 슈뢰딩거 방정식을 어떻게 푸는지나 특정 시스템의 규칙이 무엇인지 등과 같은 질문에도 믿을 수 있는 답변을 제시해야 한다.

하지만, 모두가 알듯이 ChatGPT는 science 관련 문제를 제대로 풀지는 못한다. 위와 같은 ChatGPT에 "Moledcule that cures cancer"가 무엇이고 "Room-temperature superconductor"를 어떻게 설계하는지 물어보았을 때, 우리가 얻는 것은 의미가 없는 결과들일 것이다. 왜냐하면 image data나 text data는 위와 같은 질문들에 대한 답변을 하기에는 적합하지 않기 때문이다. Image나 text는 이와 같은 중요한 scientific object와 관련해서 제대로 표현하기 어렵기 때문이다. Science 저널 등을 보게되면 수많은 diagram과 graph 기반의 구조물들을 많이 볼 수가 있을 것이다. 특히 3D와 관련해서는 voxel과 같은 여러 building block들로 연결되어 있기 때문에 이를 image나 text로 생성한다는 것에는 한계가 존재하기 마련이다. 그렇기 때문에 graph를 생성할 수 있는 deep generative model이 필요한 것이다.

Deep Generative Models for Graphs

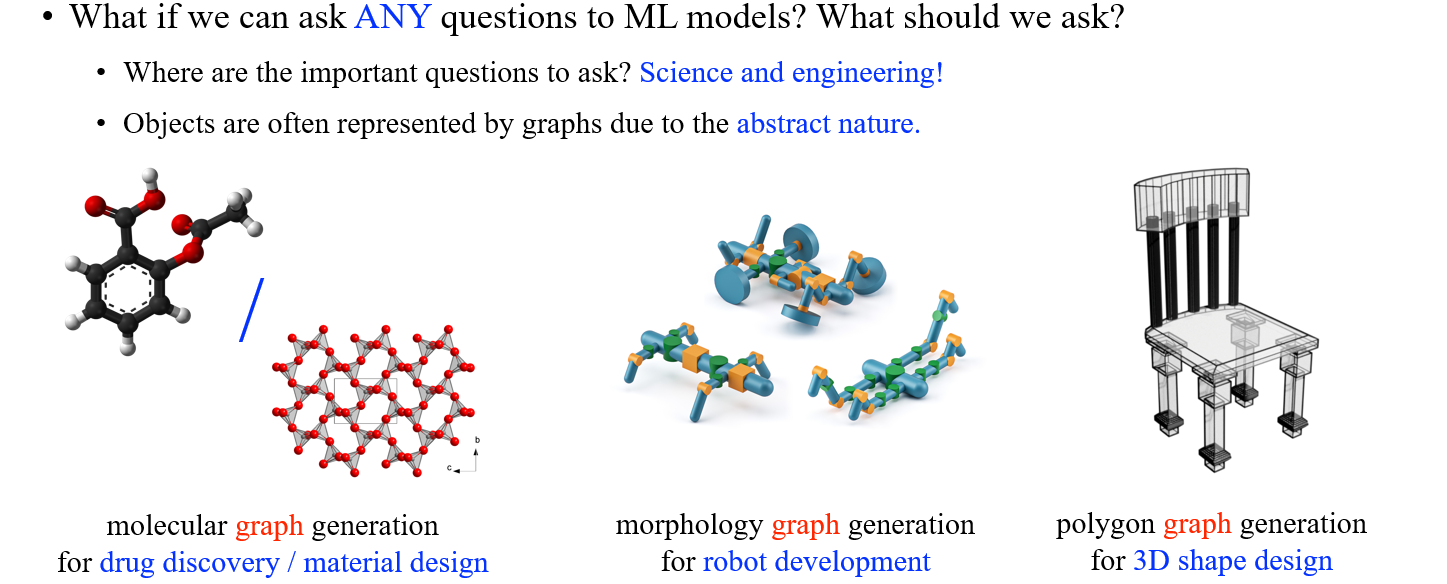이렇듯 최근에는 deep generative model을 이용하여 여러 graph를 만들고 있다. 대표적인 graph 기반의 generation task로는 molecular graph generation, morphology graph generation, 그리고 polygon graph generation 등이 있으며, 이렇게 만들어진 graph들은 신약 개발에 사용되거나 새로운 로봇을 만들거나 등에 활용될 수가 있을 것이다.

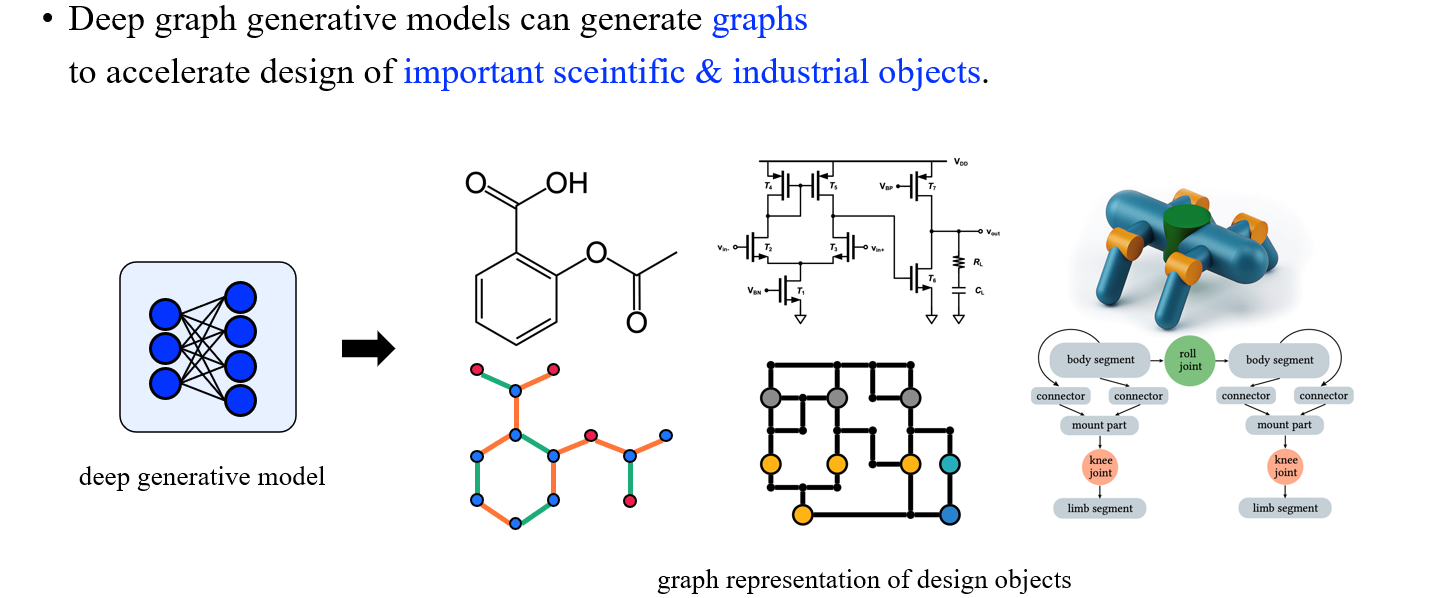Molecule이나 robot과 같은 topological data를 만들어내기 위해서 결국에는 이에 적합한 generative model을 설계하는 것이 중요하다. 결국, 우리가 deep graph generative model을 이용하여 여러 목적에 맞는 graph를 만들어 추후에 과학과 산업에 도움이 되는 것이 최종 목표라고 할 수 있다.

결국 우리가 왜 graph generative model을 설계해야하는지 묻는다면 이는 중요한 과학과 산업에서 여러 문제들을 해결하기 위해서라고 대답할 수 있다. 그리고 이와 관련하여 2가지 challenge들을 해결하는 방법들에 대해서 살펴볼 것이다.

Promise: Industry & Science

Generating Molecules

가장 먼저 알아볼 것은 molecule generation이다. Graph generative model은 새로운 약과 물질들을 만들 수 있는 molecule들을 생성할 수가 있다. 우리가 어떻게 약을 발견하고 어떻게 물질들을 발견할 수 있는지와 관련해서 여러 산업에 도움을 줄 수 있다.

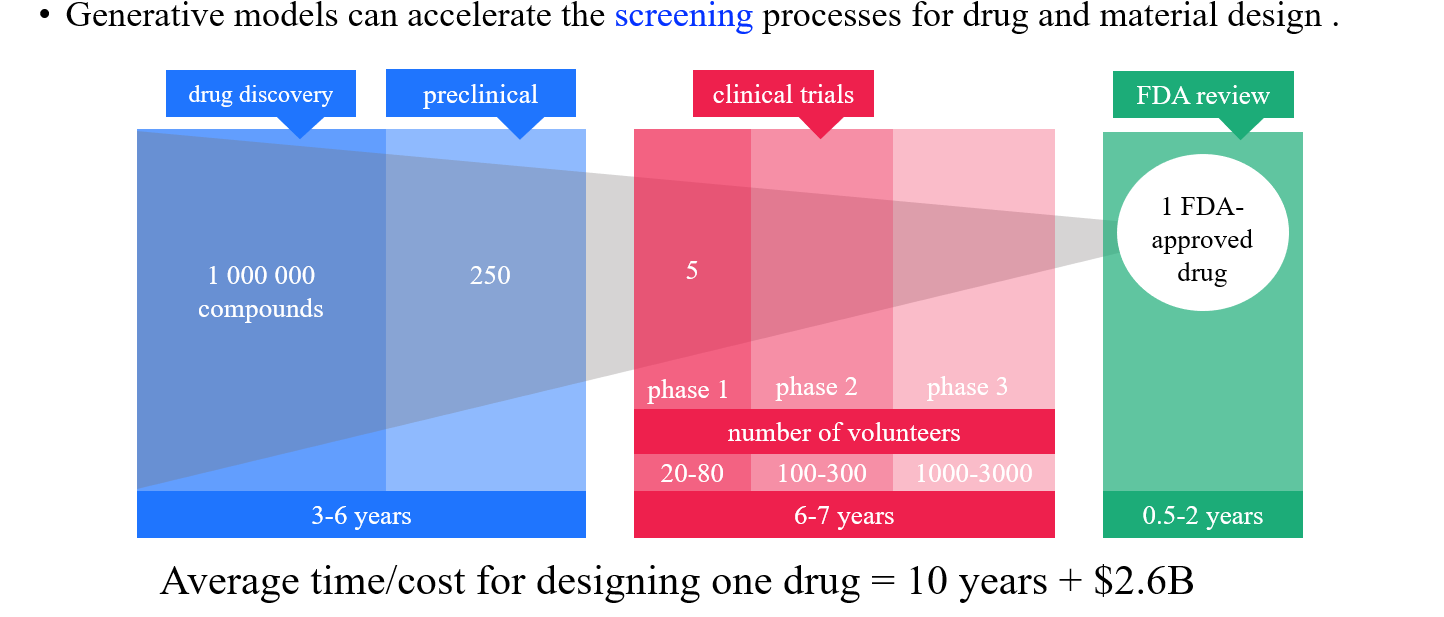특히 이와 관련된 산업들의 규모는 실제로 굉장히 크다. Comuputer science에서 지원받는 자금들과 비교해서 medical/life science가 지원받는 금액들을 살펴보면 실제로 규모가 얼마나 큰지 확인할 수 있다. 그리고 실제 하나의 신약을 개발하는데 들어가는 시간은 약 10년 정도로 그 기간이 상당한 것을 알 수 있다. 우리가 인공지능 모델을 이용해서 이러한 문제를 직접적으로 해결할 수는 없겠지만, 신약을 개발하는 이러한 과정을 가속화시키는데 도움을 줄 수는 있을 것이다.

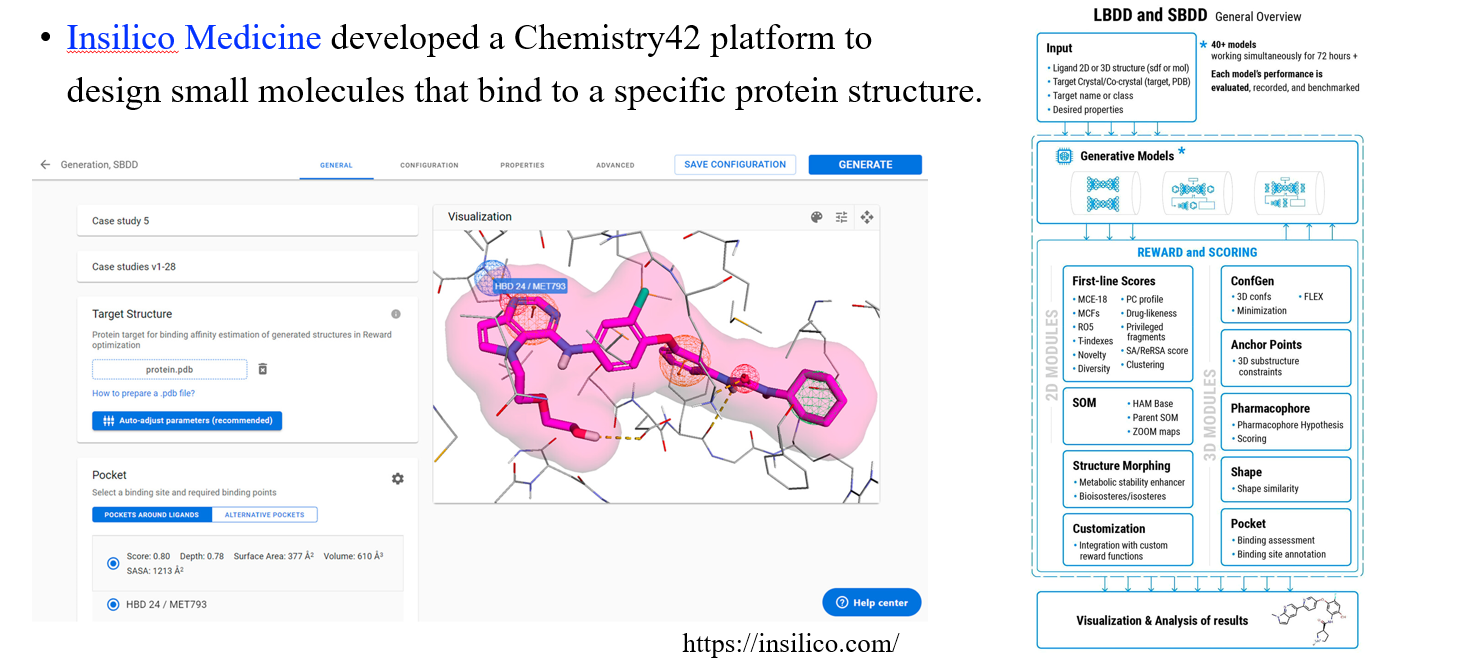Insilico Medicine은 신약 발굴을 위한 AI 플랫폼을 개발한 회사로 위와 같이 특정 protein structure들을 엮을 수 있는 molecule들을 설계할 수 있는 플랫폼을 개발하기도 하였다.

Reaction and Retrosynthesis Prediction

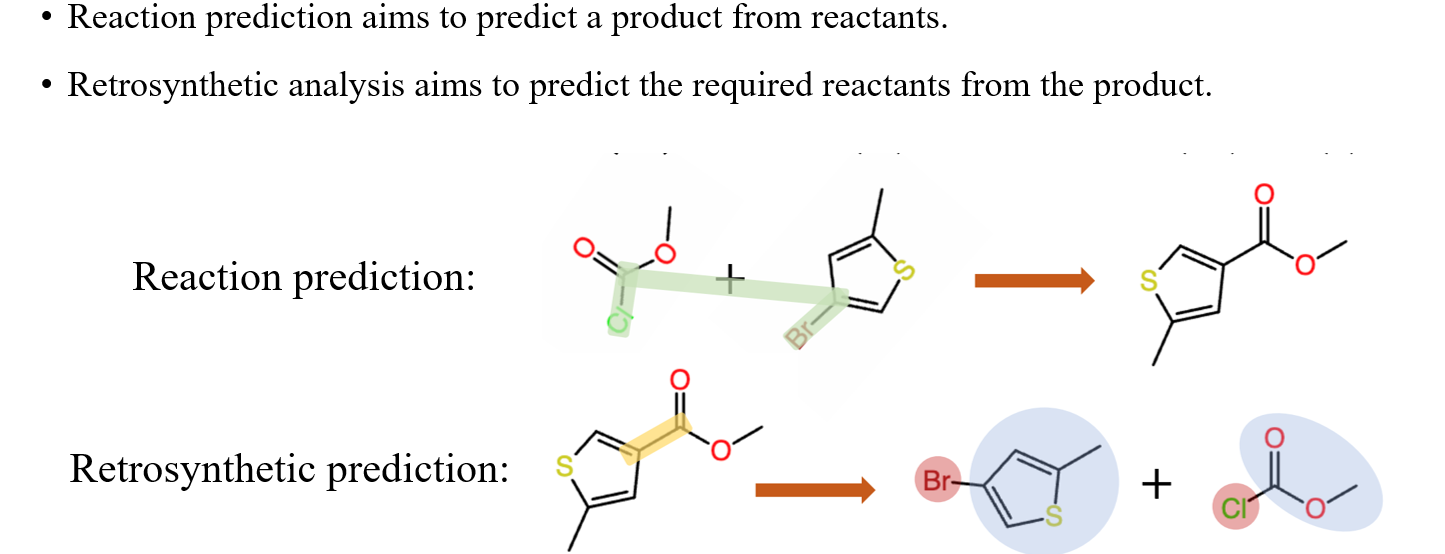Graph generation model은 또한 reaction prediction이나 retrosynthesis prediction에도 사용될 수 있다. Reaction prediction은 반응물로부터 어떠한 화학 반응이 일어날지 예측하는 것이고, retrosynthesis prediction은 기존의 화학 반응으로부터 어떠한 반응물들이 필요하는지를 예측하는 것이다.

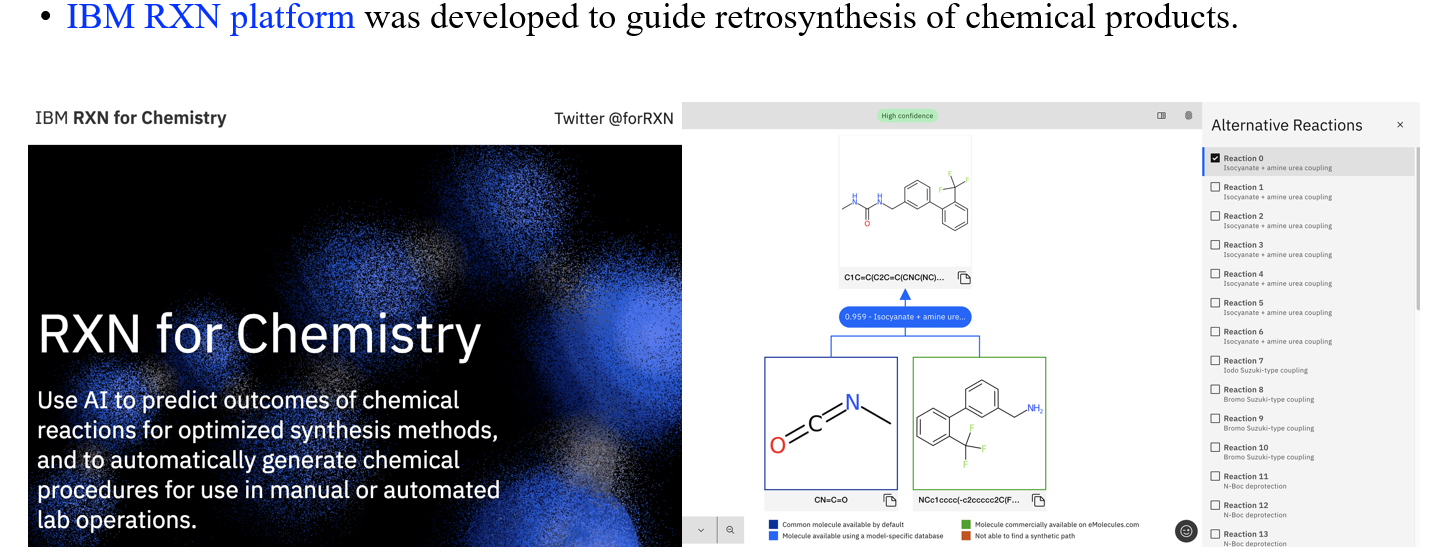IBM은 실제로 이러한 반응들을 예측할 수 있는 platform을 개발하기도 하였다.

Robot Morphology Graph Generation

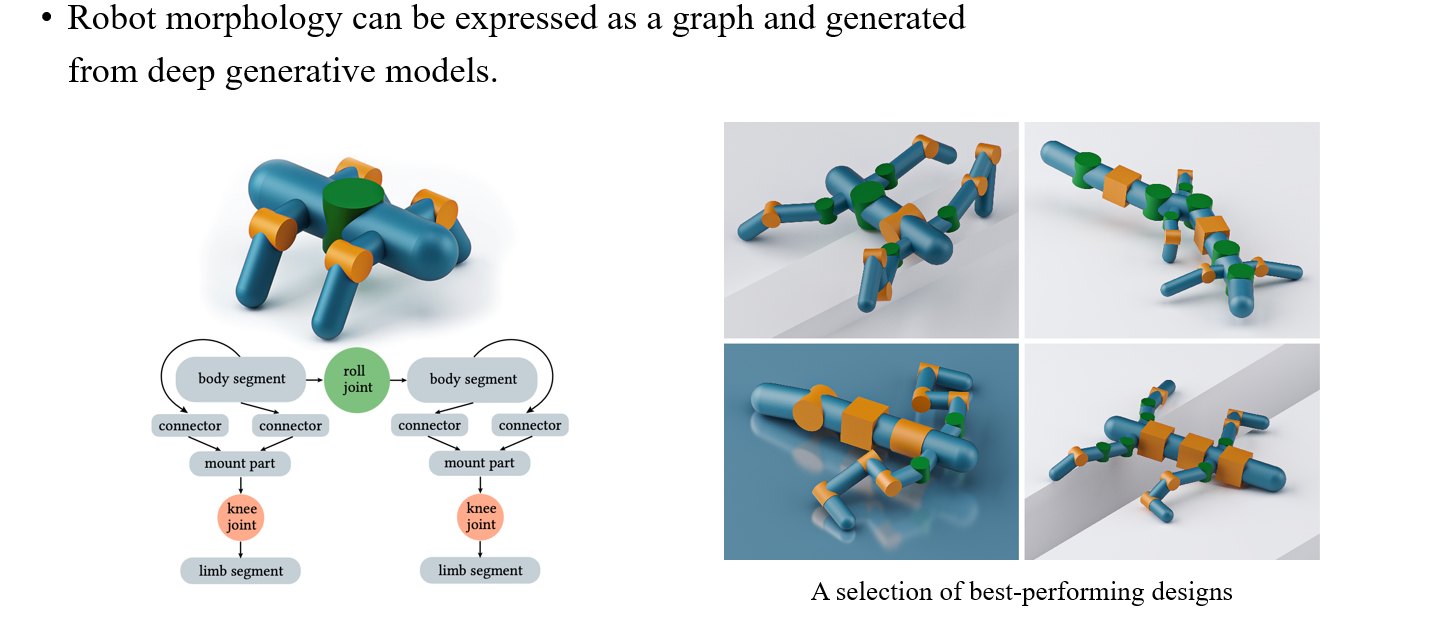Robot morphology는 로봇의 형태와 관련한 분야로, 이는 graph로 표현될 수 있어서 gerative model로 이 또한 생성할 수가 있다. 그래서 어떠한 로봇이 계단을 오른다고 했을 때 이 로봇이 어떠한 형태로 되어있어야 하는지를 generative model이 예측해서 만들 수가 있다.

Scene Graph Generation

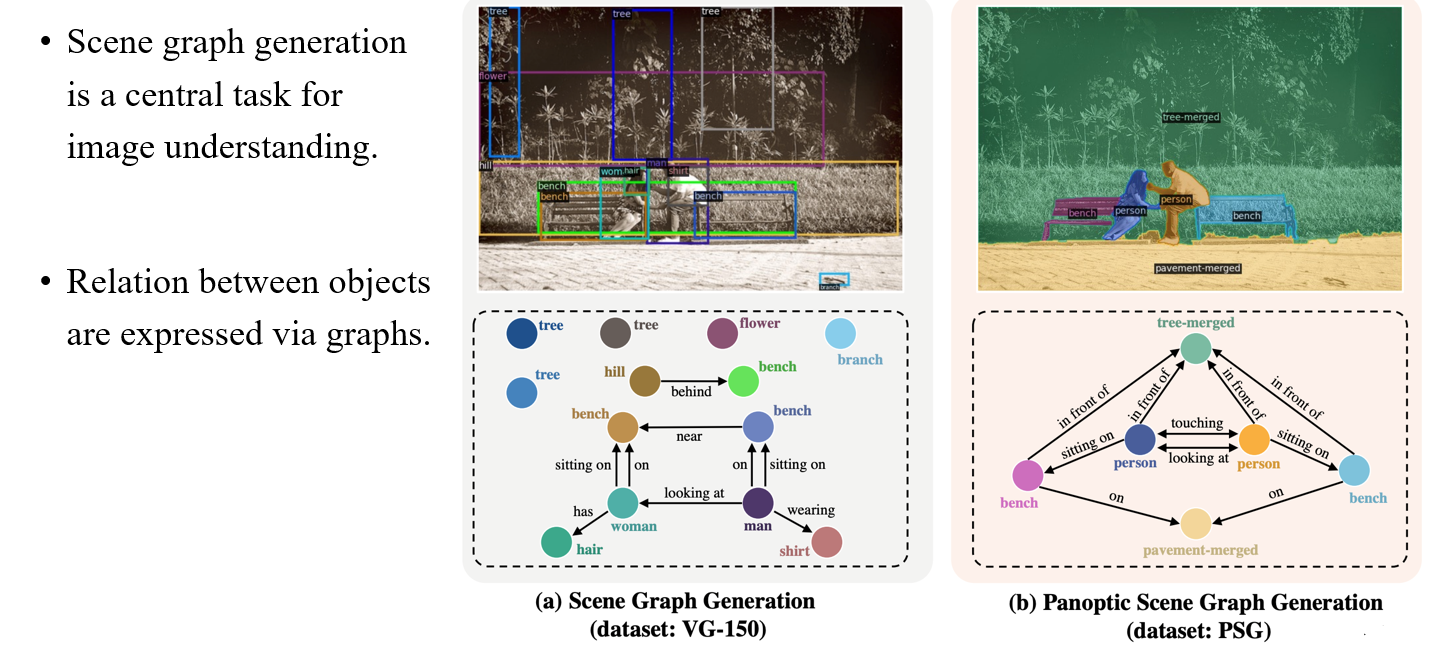Computer vision 분야에도 graph와 관련해서 유명한 task가 존재한다. 바로 각각의 object를 graph로 표현하여 해당 장면을 예측해야하는 scene graph generation이다. 하나의 image를 graph로 표현하여 각각의 물체와 이 물체간의 관계를 설명할 수 있는 것이다.

Polygon Generation

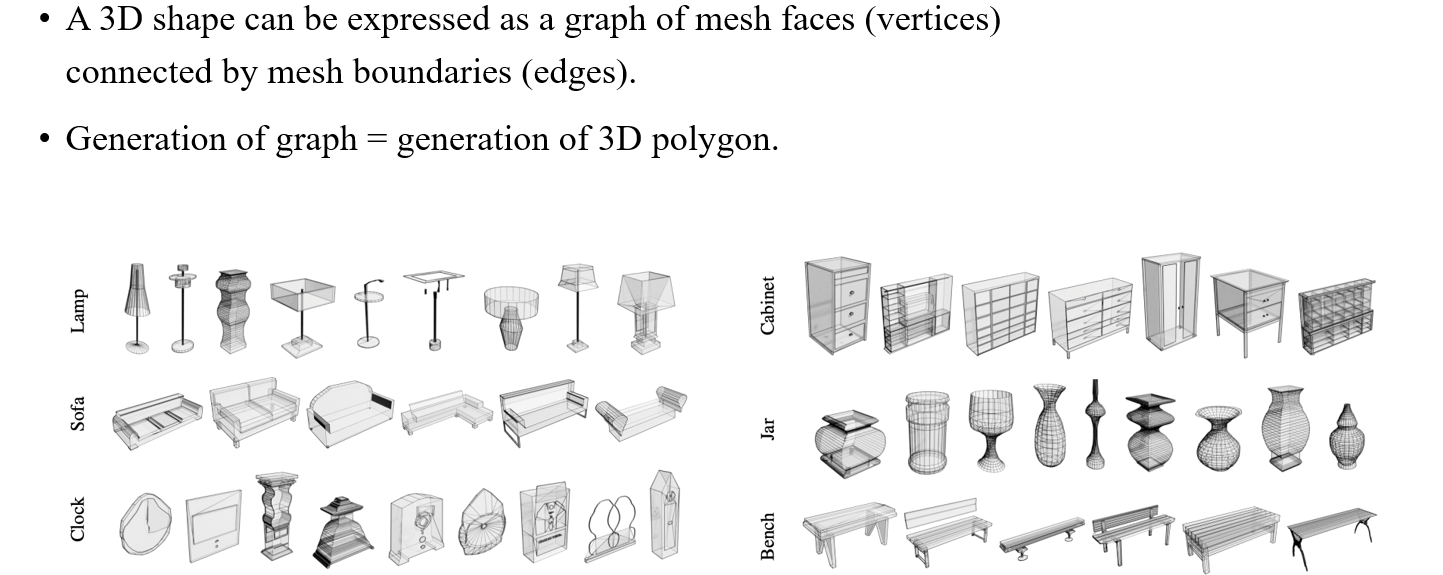Polygon generation은 3D shape을 설계하는 것이 목적이다. Mesh의 face가 graph에서의 node가 되고, mesh의 boundary가 graph에서의 edge가 되는 것이다. 따라서 3D polygon을 생성한다는 것은 graph를 만드는 것과 동일하게 볼 수 있다.

Basics: Graph Generative Models

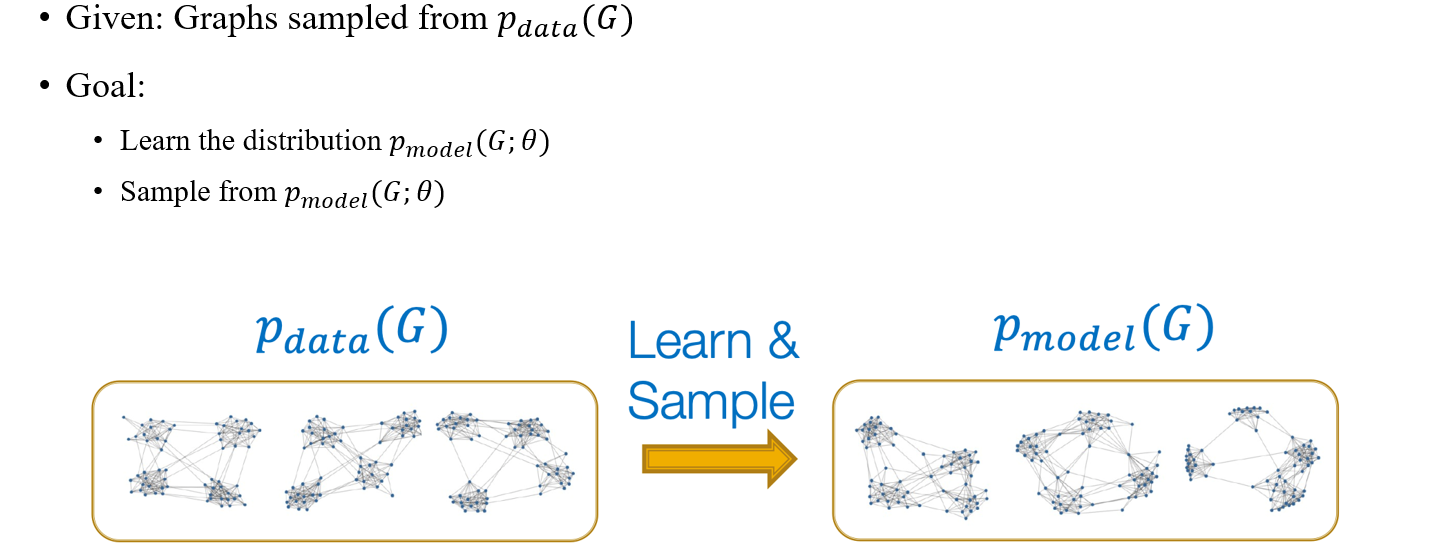Graph generative model에 대해서 본격적으로 알아볼 것이고, 가장 먼저 어떻게 문제 정의를 하는지 보고자 한다. 우리는 graph dataset에 초점을 두고 각 graph $G$는 data distribution $p_{data}(G)$로부터 sampling된다고 가정하자. 이러한 distribution을 기반으로 model이 새로운 model distribution $p_{model}(G;\theta)$ 학습할 것이고, 새로운 graph가 이로부터 sampling 될 것이다.

우리는 가장 직관적인 방법 중 하나인 autoregressive model에 대해서 먼저 알아볼 것이다. Autoregressive model은 distribution을 chain rule로써 표현할 수 있고, graph를 sequence로 parameterization하여 표현하게 된다. 그래서 autoregressive model은 model distribution $p_{model}$을 만들어 density estimation과 sampling에 사용하는데, 이때 chain rule을 사용하여 위와 같이 joint distribution을 각각의 conditional distribution들의 곱으로 표현하게 된다. 여기서 각 $x$는 특정 graph에 해당하고, $x_t$는 이전의 graph를 기반으로 특정 $t$번째 action을 설명하게 된다. 아무것도 없는 공간에 vertex를 추가하고 edge를 추가하고 또 vertex를 추가하는 등의 행동을 반복해서 최종 graph를 구성하게 되는 것이다. 그래서 각 시점의 graph에 대한 conditional graph를 모두 곱하여 model distribution을 나타내는 것이고, autoregressive model은 이러한 action 하나하나를 예측하게 되는 것이다.

GraphRNN Idea

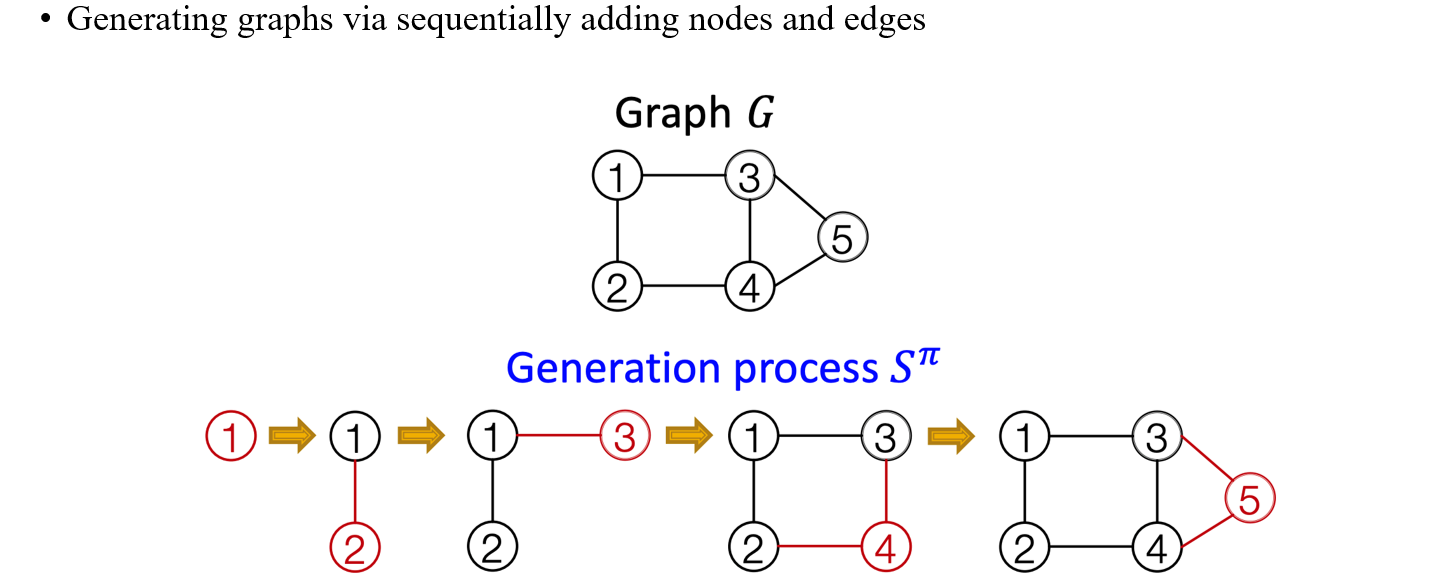가장 유명한 graph generative model 중 하나는 GraphRNN로, 연속적으로 vertex와 edge를 연결시켜서 graph를 만들게 된다. 이를 위해서 가장 먼저 vertex에 ordering을 해야한다. 1번 vertex를 만들고 2번 vertex를 만든 다음에 이를 연결하는 edge를 추가해준다. 그다음에 3번 vertex를 만든 다음에 1번 vertex와 연결하는 edge를 추가한다. 이러한 식으로 각 vertex에 특정 순서를 매겨서 graph를 만들어나가는 것이 GraphRNN의 아이디어이다.

Model Graphs as Sequences

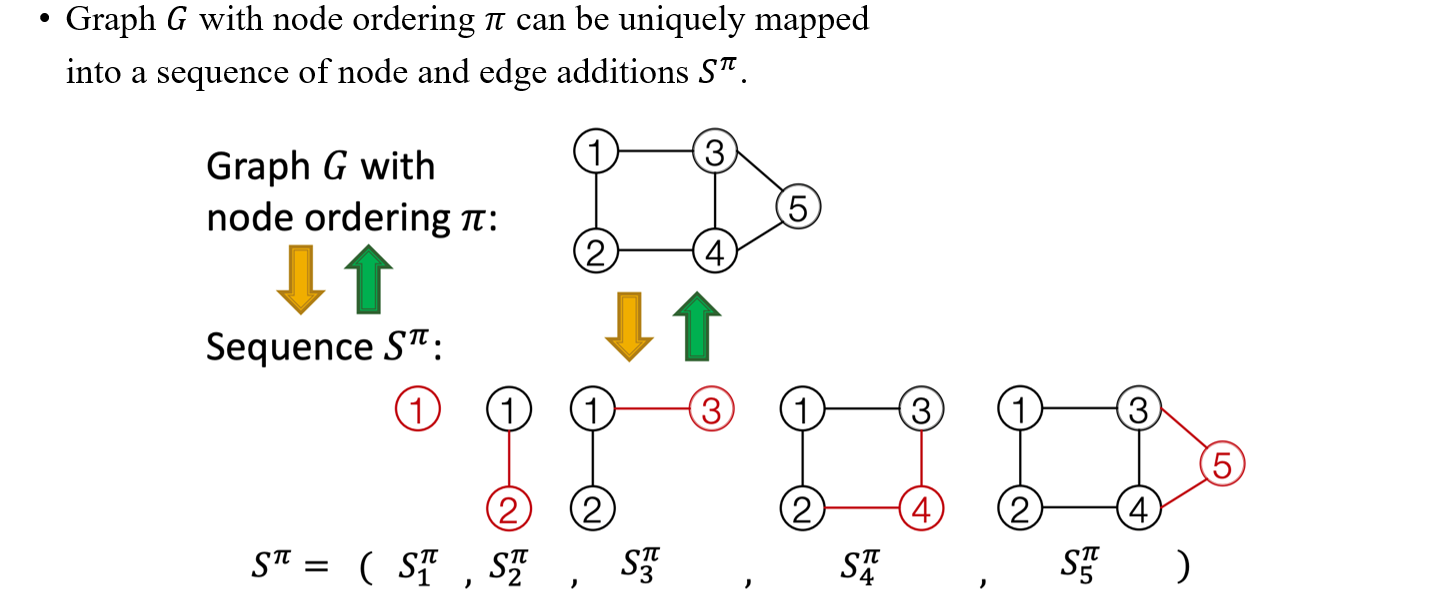개념적으로는 정말 간단하나 실제로 어떻게 vertex를 추가해서 graph를 만들어나가는지 알아보고자 한다. 이는 text generation model과 비슷한 맥락에서 이해할 수 있다. 각각의 action을 vertex를 추가하는 것으로 본다면 이러한 action들의 sequence $S^\pi$를 우리는 구할 수 있을 것이다. 즉, 첫번째 vertex를 추가하는 action을 sequence $S^\pi_1$로 보고, 두번째 vertex를 추가하는 action을 sequence $S^\pi_2$로 생각할 수 있을 것이다. 각각의 action들을 전부 모아서 sequence $S^\pi$를 만들게 되면 마지막에 우리는 하나의 완성된 graph를 얻게되는 것과 같아진다. 여기서 $S^\pi_1, S^\pi_2, ...$를 우리는 discrete word, vocabulary, text 등으로 간주할 수 있다.

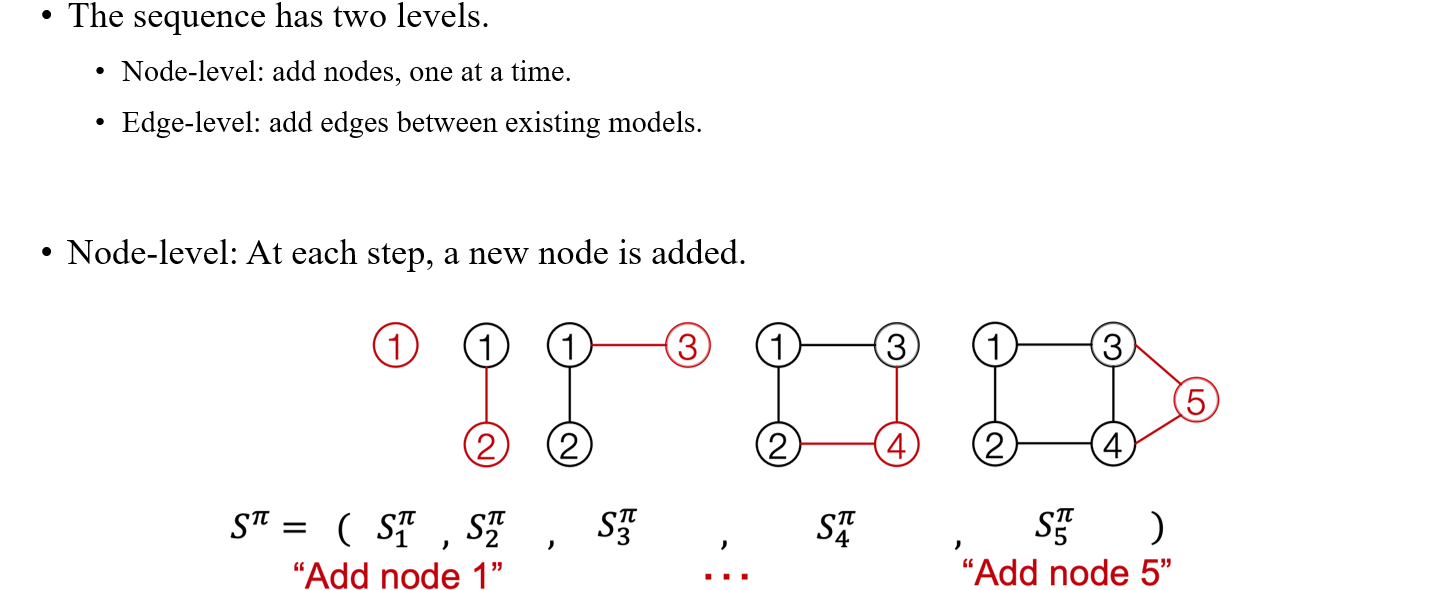이러한 식으로 만들어지는 graph는 node ordering으로 정의되어진 것이다. 각 node에 숫자를 부여하게 되면 순서에 맞게 node가 추가되는 식으로 graph를 만들 수 있는 것이다. 그렇다면 컴퓨터는 이러한 ordering을 어떻게 이해해서 쉽게 graph를 만들 수 있는 것일까? 지금까지는 하나의 node를 한번씩 추가하는 방식으로 graph를 만들었지만, 이외에도 edge를 추가해서 graph를 만드는 방법도 존재하게 된다. 실제로 node ordering에서는 vertex를 추가할 때마다 연결되는 edge도 자동으로 추가되고 있는 것이다.

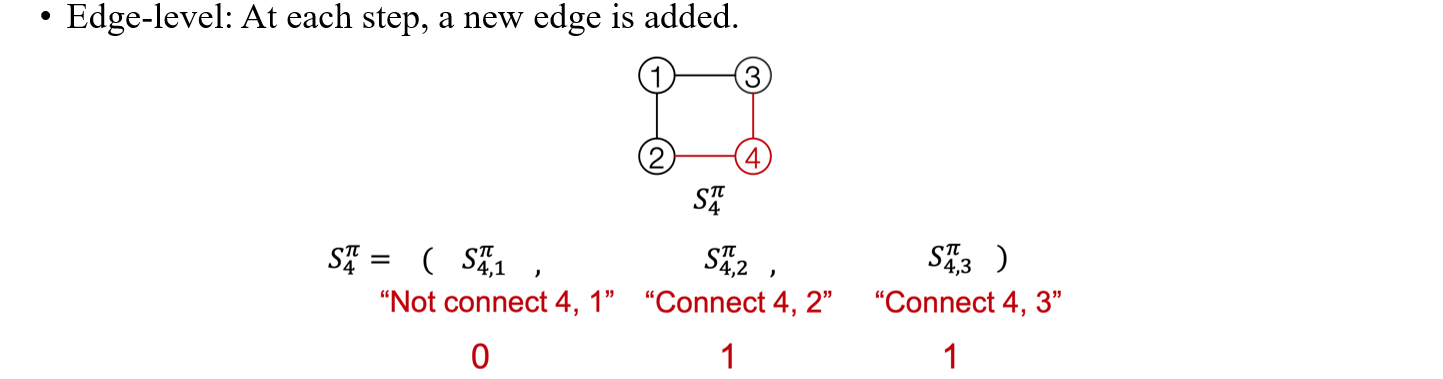Edge-level에서 4번째 vertex를 추가하는 sequence $S^\pi_4$를 보면 순서대로 해당 vertex와 edge가 연결되어 있는지를 binary 숫자를 이용해서 나타낼 수가 있다. 예를 들어, 위의 그림에서 4번 vertex는 1번과는 연결되어 있지 않고 2,3번과 연결되어 있기 때문에 $S^\pi_4$가 0,1,1이 되는 것이다. 그래서 만약 특정 sequence가 011로 표현되어 있다면, 이는 4번째 vertex를 추가하는데 있어 2번째와 3번째 vertex와 연결되어 있음을 해석할 수가 있다.

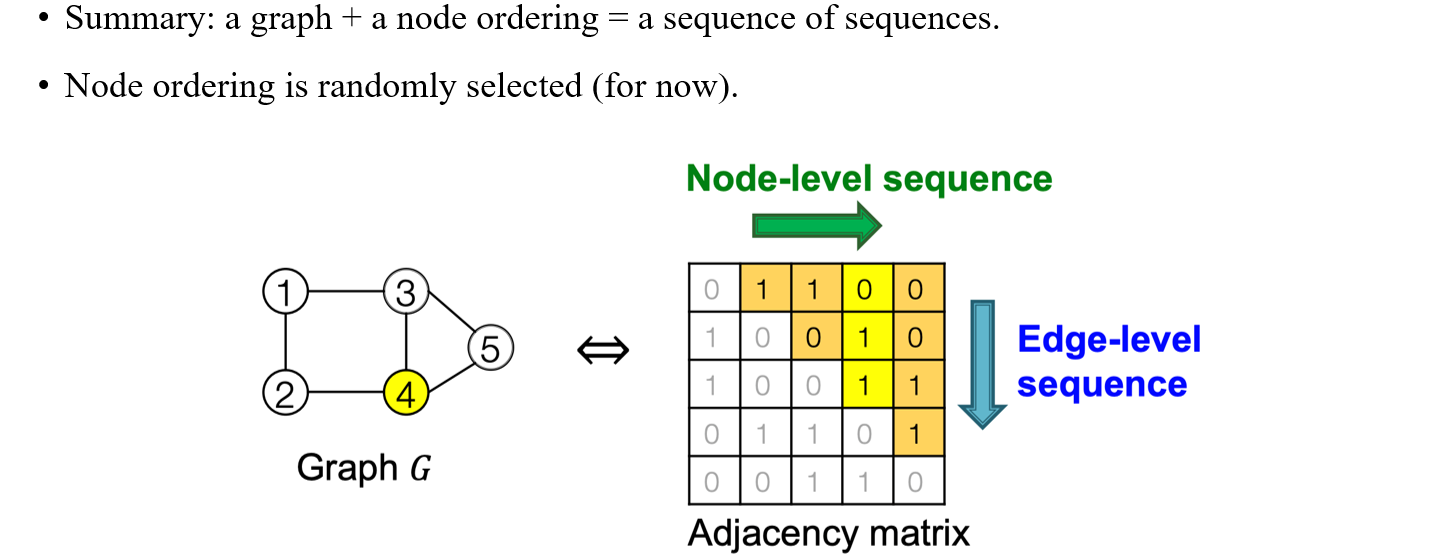정리하자면 우리가 어떤 graph와 node ordering이 주어졌을 때, 우리는 이를 sequence들의 sequence로 해석할 수가 있게 된다. 각각의 vertex에 대응하는 sequence가 존재하고, 이들을 전부 모아놓은 sequence가 graph가 되기 때문이다. $S_2$의 경우에는 1번과 연결되어 있어서 1이고 $S_3$의 경우에는 1번과 연결되어 있고 2번과 연결되어 있지 않아서 10이고 $S_4$의 경우에는 1번과 연결되어 있지 않고 2,3번과 연결되어 있어 011인 것이다. 이들을 잘 모아서 adjacency matrix로 해석하면 upper traingle이 바로 graph가 어떻게 구성되어 있는지를 나타내고 있는 것이다. 따라서 GraphRNN은 이러한 graph를 sequence로 만들고자 하는 방법이고, 각 sequence를 하나의 column으로 하는 adjacency matrix를 구성해야 하는 것이다.

GraphRNN: Two Levels of RNNs

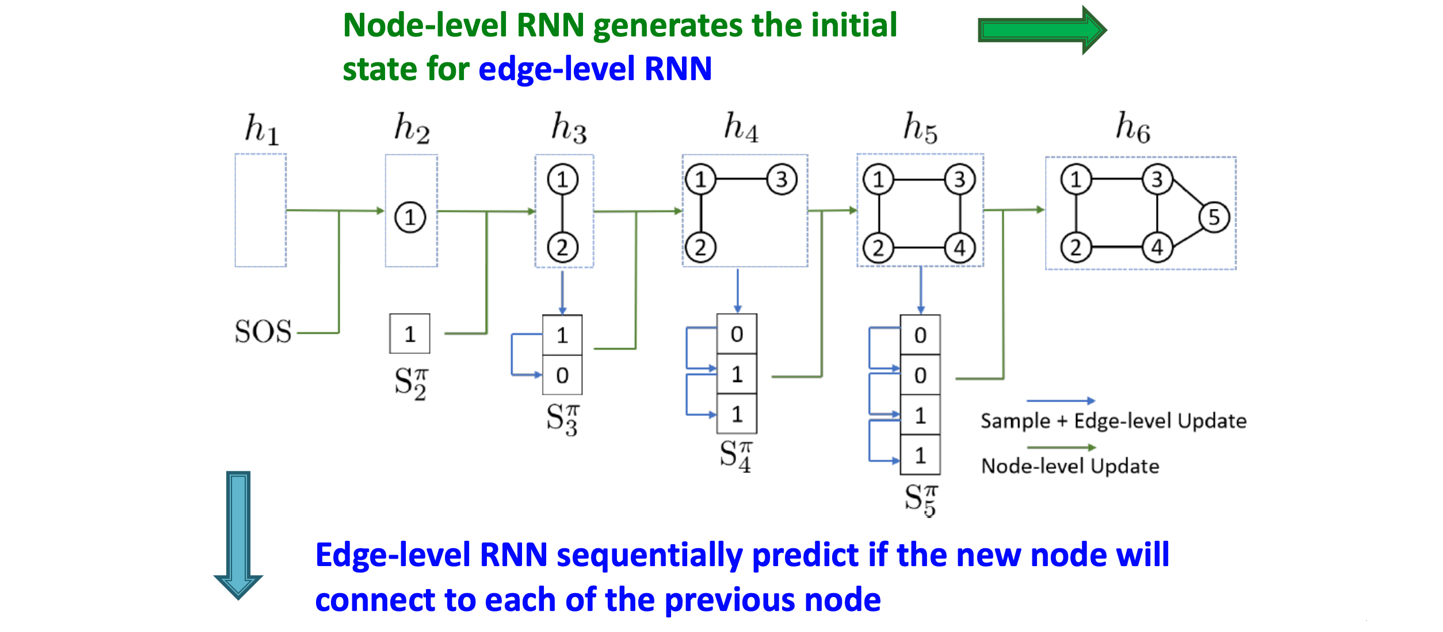이렇듯 GraphRNN은 node level과 edge level로 구성되어 two level로 볼 수 있다. 특히 RNN구조가 node level에서 먼저 이루어지고 이후에 edge level에서 이루어져 two level RNN으로 설명이 가능한 것이다.

Issue: Tractability

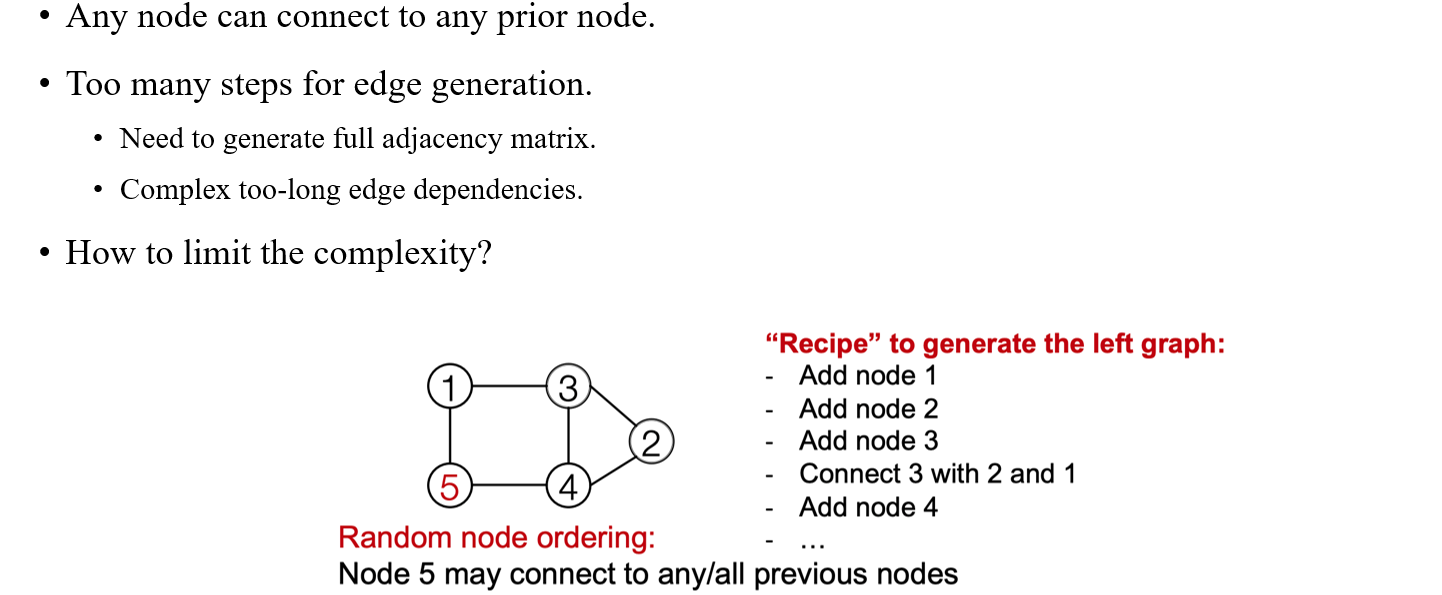이렇게 graph 하나를 만드는데 two level로 만들다보면 다소 복잡하다고 생각할 수 있다. GraphRNN은 정말로 유명한 baseline 중 하나이기 때문에 어떻게 보면 문제점이 다수 존재하는 모델로 파악될 수 있다. 가장 대표적으로 graph의 tractability가 문제점 중 하나이다. 이것이 의미하는 바는 우리가 GraphRNN을 실행시켰을 때 complexity가 높다는 것을 의미하게 되어 edge generation을 하는데 있어서 너무 많은 step이 필요하게 된다. 우리가 1,000개의 vertex가 있을 때 1,000,000개의 edge를 만들어야 하는 상황이 생길 수도 있게 된다. 이렇듯 random node ordering의 경우 edge generation시 이전의 모든 vertex들을 고려해야해서 complexity가 증가하게 된다.

그래서 사람들은 이러한 complexity를 어떻게 하면 줄일지 생각하게 되었다. 사실 대부분의 graph는 굉장히 sparse한 형태로 존재하게 된다. 우리가 이러한 sparsity만 가정하고 보장할 수 있다면 평소보다 빠르게 graph를 만들어낼 수 있을 것이다.

Solution: Tractability via BFS

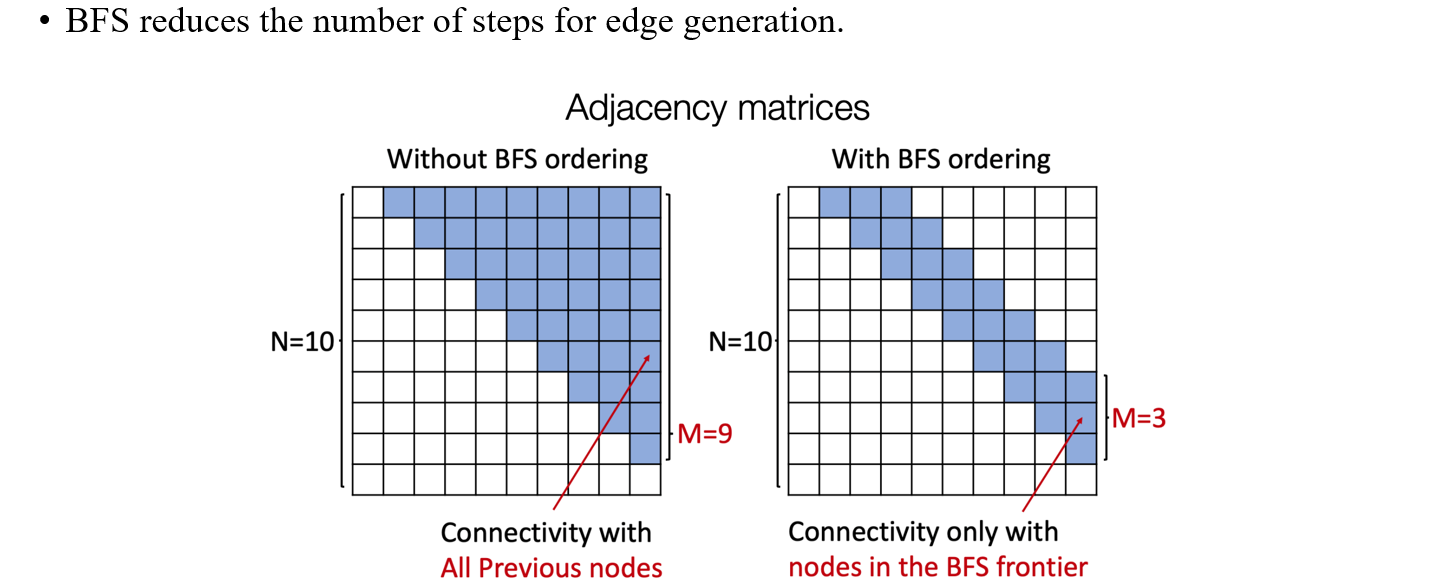이러한 sparsity를 가정하고 사람들은 Breadth-First Search(BFS)를 이용해서 실질적으로 기존의 tractability 문제를 해결하려고 했다. 그렇다면 왜 BFS일까? 바로 BFS가 가지는 powerful한 가정때문이다. 만약 우리가 BFS를 graph에 적용하게 된다면 random ordering과는 다르게 tree가 만들어지고, 이 tree는 width의 크기가 제한될 것이다. 이를 adjacency matrix의 관점에서 본다면 0으로 채워지는 공간이 생겨 결과적으로 연산량이 크게 줄어들게 될 것이다.

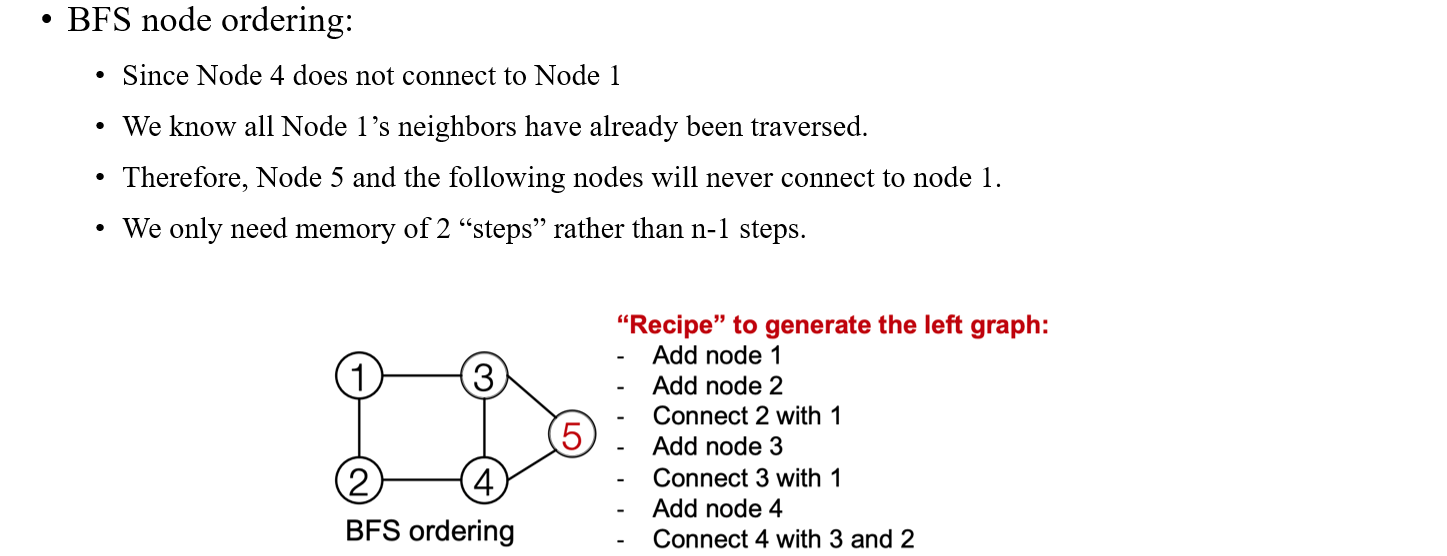쉽게 생각해보면 BFS에 따라 인접한 vertex들에 따라 node ordering을 진행하게 되면 해당 경우의 수가 상당히 줄어들고, 인접한 vertex들과의 관계만 고려할 수 있기 때문에 기존의 문제중 하나였던 long-term dependency 문제도 해결할 수 있게 된다. 위의 예시에서 node 5를 만든다고 해보자. 이미 node 1~4까지는 추가가 된 상태이다. 여기서 우리는 BFS를 사용했기 때문에 node 5가 node 4 이전에 만들어졌다는 가정을 없애도 되는 것이다. 그렇다면 node 4번보다 더 먼저 추가가 되어지고 이후에 node 4가 추가되어야 되기 때문에 BFS를 사용하는 순간부터 강력한 조건을 달고 graph를 만들어나갈 수 있는 것이다.

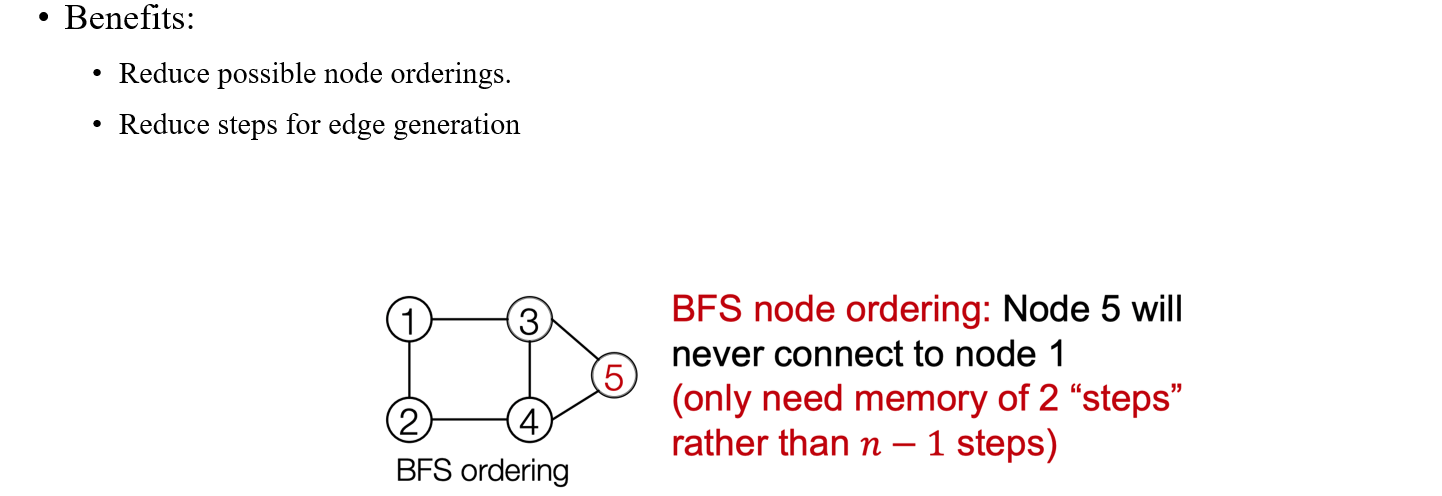만약 node 4가 node 1과 연결되어 있지 않고 node 5가 node 4와 연결되어 있다면 node 5는 자연스럽게 node 1과 연결되어 있지 않음을 파악할 수도 있다. 이렇듯 BFS를 사용하면 node ordering의 경우를 줄일 수 있음과 동시에 edge generation의 step도 줄일 수 있게 된다.