이전에 살펴본 GraphRNN과 BFS를 사용하는 방법이 graph를 생성하는 대표적인 방법 중 하나였고, 많은 문제를 해결할 수 있는 좋은 방법이었다. 하지만 이렇게 좋은 방법이 있음에도 불구하고 연구자들은 계속해서 다양한 연구를 진행하고 이로 인해 다양한 방법들이 계속해서 등장하게 된다. 이번에는 기존의 GraphRNN 이후 연구되었던 대표적인 2가지 방향성에 대해서 알아보고자 한다.
Research Direction 1: Generative Grammar
첫번재로 어떻게 generative grammar를 찾을 수 있는지, 어떻게 연속적으로 graph를 만들 수 있는지에 대해서 알아볼 것이다.
Graph Generation Grammar
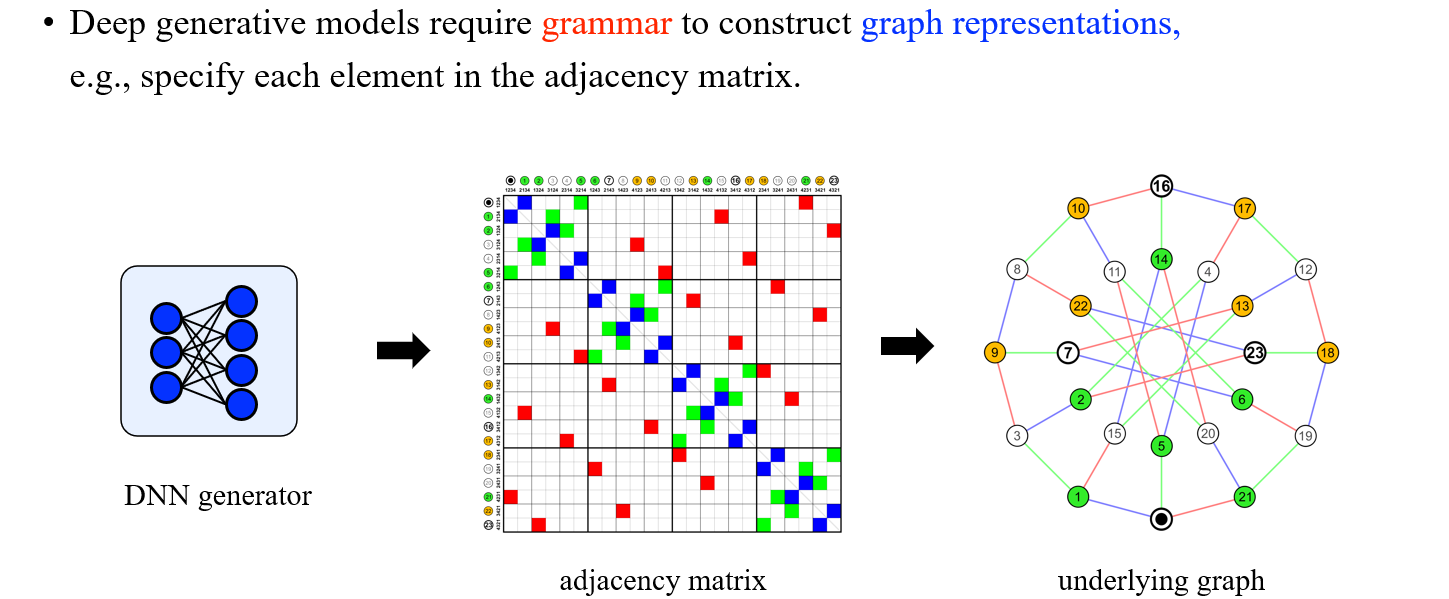기존의 adjacency matrix가 graph를 표현하기에 좋은 수단임에는 틀림이 없다. 하지만 adjacency matrix 외에도 graph를 표현할 수 있는 다양한 좋은 수단들이 존재할 수 있다. 이렇듯 상황에 맞게 grammar를 사용하는 방법이 deep graph generative model로 하여금 좋은 graph representation을 나타낼 수 있게 해주고, 대표적인 예시 중 하나가 adjacency matrix에서 각각의 element를 명시하는 것이다.
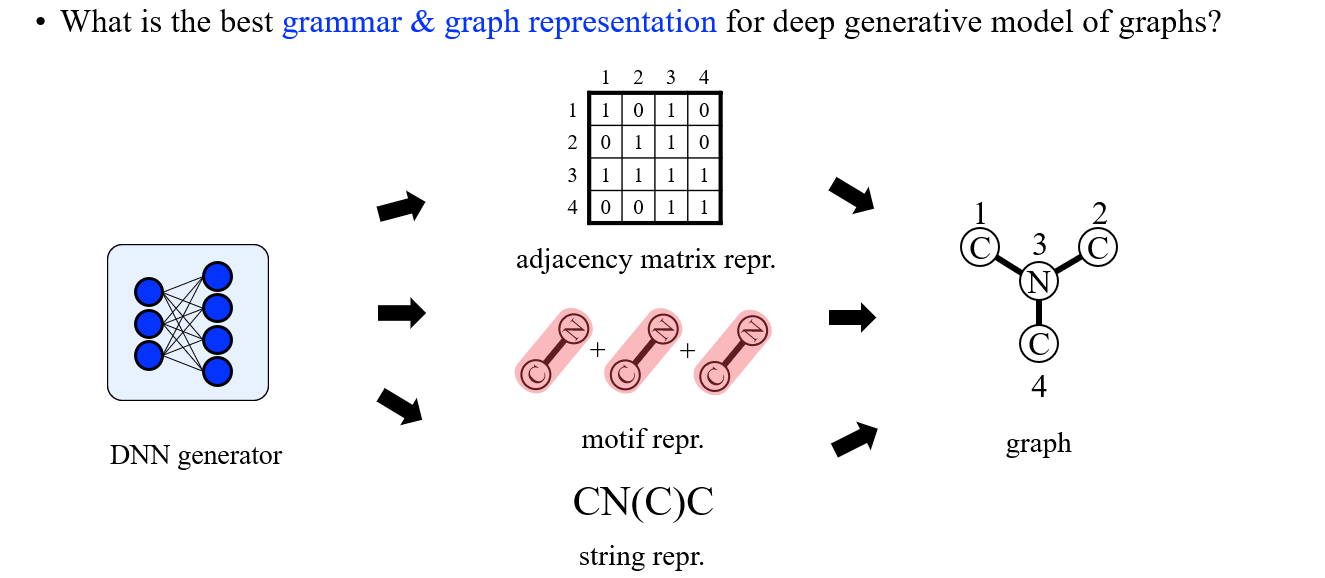Adjacency matrix가 좋은 방법이지만 graph type을 명시하는데 있어서는 좋지 않다고 말하곤한다. 만약 graph의 크기가 크다면 adjacency matrix로 graph를 나타내는 것은 어려움이 존재할 수 있다. Molecule의 경우 의미있는 chemical fragment로 분해가 되어 motif와 같은 수단으로 표현이 가능할 것이다. 우리는 상황에 맞게 graph를 표현할 수 있는 방법을 찾아서 graph를 효율적으로 명시하고 생성해야할 필요가 있다.
1) Adjacency Matrix-based Graph Generation
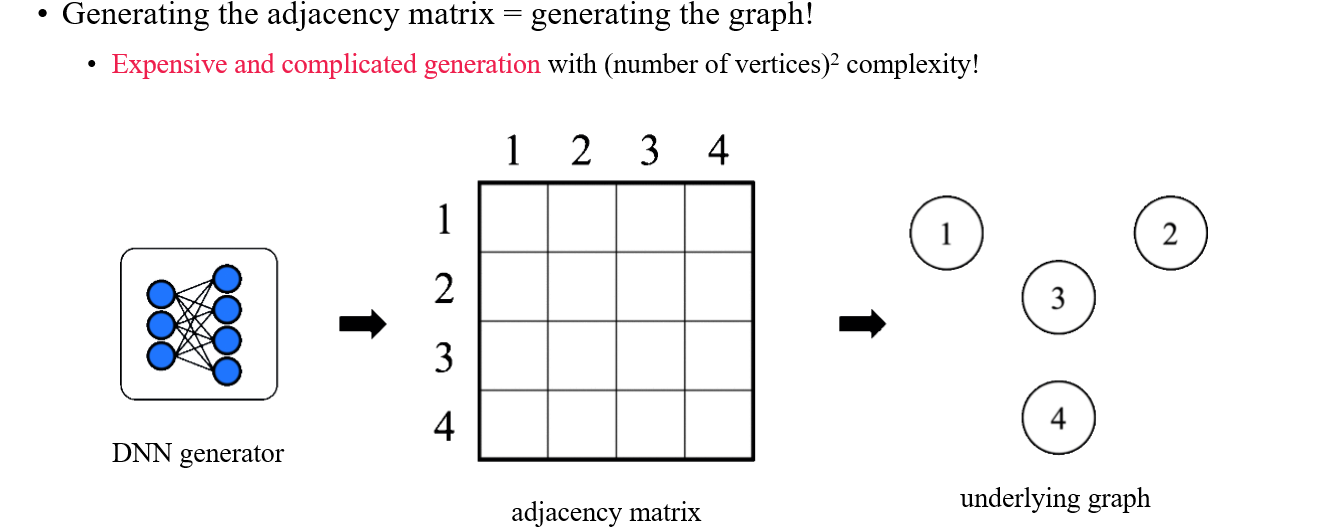Graph를 표현하는 가장 유명하고 쉬운 방법은 앞서 이야기한 adjacency matrix를 사용하는 것이다. 하지만 adjacency matrix를 사용하게 되면 generation을 하는데 있어서 complexity적인 문제가 발생하게 된다. Vertex 개수의 제곱만큼의 complexity가 생기기 때문에 graph의 크기가 큰 경우에는 사용하기 적합하지 못할 것이다.
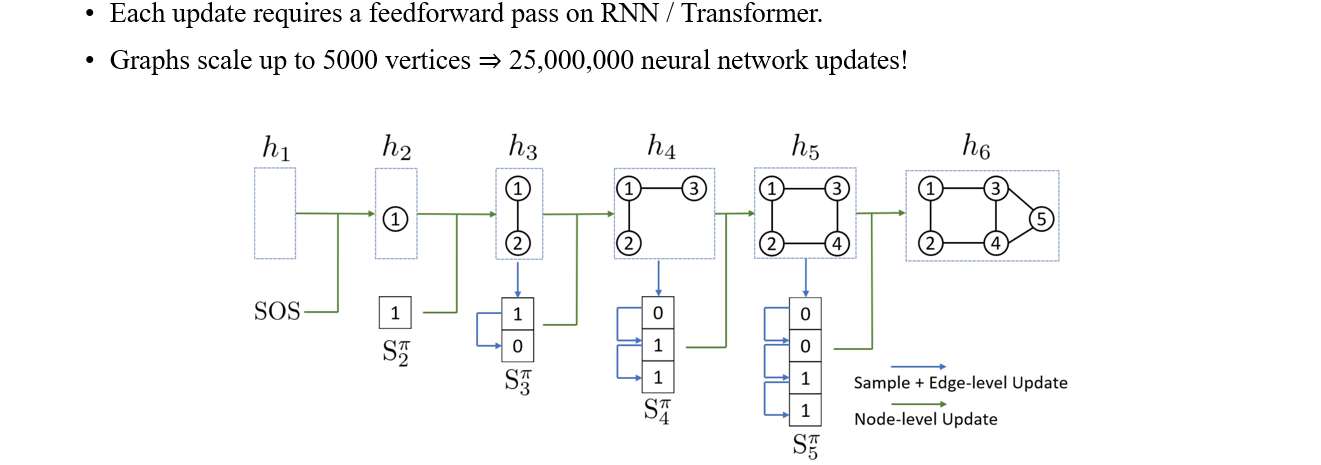만약 5,000개의 vertex가 있는 graph를 가지고 adjacency matrix를 만들어 GraphRNN을 사용하게 된다면, 25,000,000번 가량의 edge generation step이 필요하게 될 것이다.
2) {Motif, Fragment}-based Graph Generation
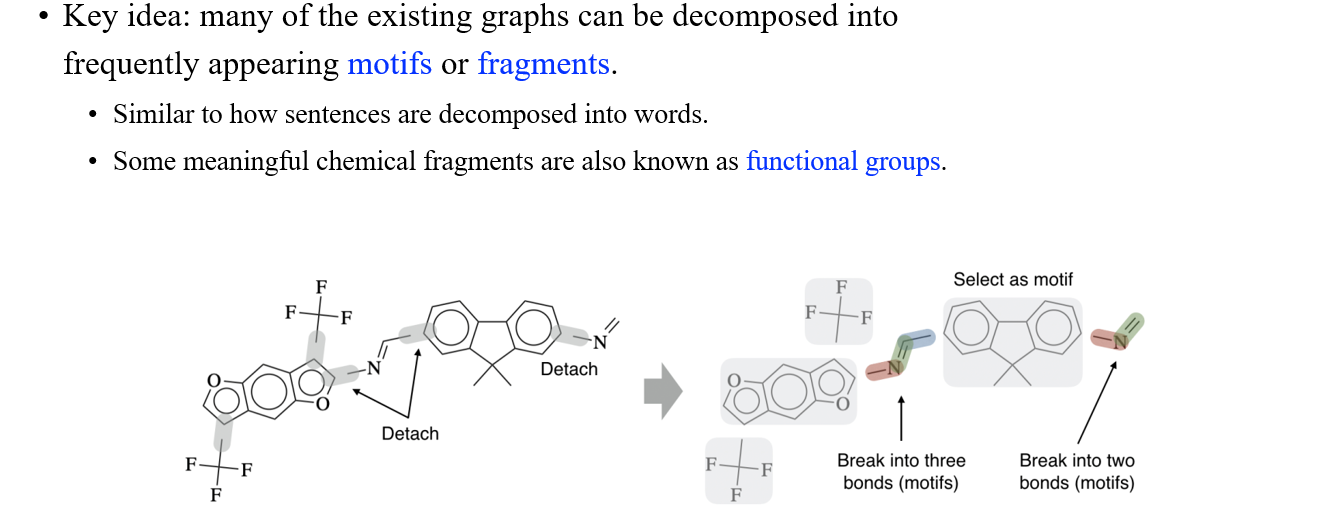그래서 사람들은 molecule과 같은 특정 type의 graph 대해서는 adjacency matrix 대신에 motif와 fragment 등을 사용해서 이를 나타내기로 했다. Molecule을 보면 ring이라고 불리는 의미있는 fragment들로 구성된 것을 볼 수 있다. Ring은 cycle과는 좀 다른 구조로 atom들의 집합으로 구성된다. 위의 그림에서 ring은 5개 혹은 6개의 atom으로 구성되어 있는 것을 볼 수 있다.
우리는 이제 어떠한 fragment가 정말로 의미있는지를 확인할 수 있다. Text dataset에서 sequence로부터 어떠한 word가 의미있는지를 파악하는 것과 같은 맥락이다. 여러 의미있는 chemical fragment들이 이어져서 하나의 molecule을 구성할 수 있고, 우리는 이를 functional group으로 여기게 된다.
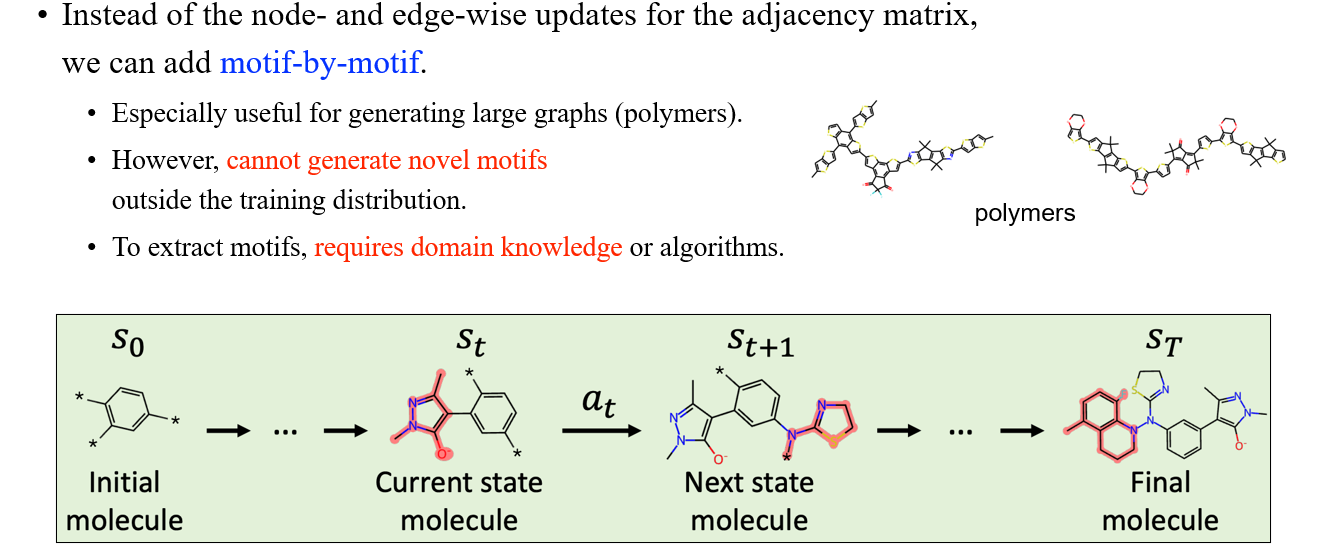위와 같이 초기의 molecule 상태에서 fragment들을 이어 붙이면서 graph를 update하게 된다. 우리는 큰 chunk 단위로 하나씩 이어붙이기 때문에 node 단위로 이어 붙이던 방식과 비교했을 때 graph의 규모를 더 빠르게 키워나갈 수 있게 된다. 하지만, 이러한 방식은 전혀 보지 못한 motif를 만들어낼 수가 없다는 단점이 있다. 그래서 우리가 motif를 추출하고 생성하기 위해서는 domain knowledge가 부가적으로 필요하다는 것이 이 방식의 문제점 중 하나이다. 이렇듯 chemical knowledge를 generative model에 포함시키는 부분이 굉장히 중요한 요소이다. 사실 우리가 fragment를 가지고 있다고 하더라도 실제로 어디에 붙여야하는지가 상당히 어려운 문제이고, 또한 이어 붙인다고 하더라도 하나의 edge로 연결해야하는지 2개의 edge로 연결해야하는지 등의 다양한 문제에 직면하곤 한다.
3) String-based Graph Generation
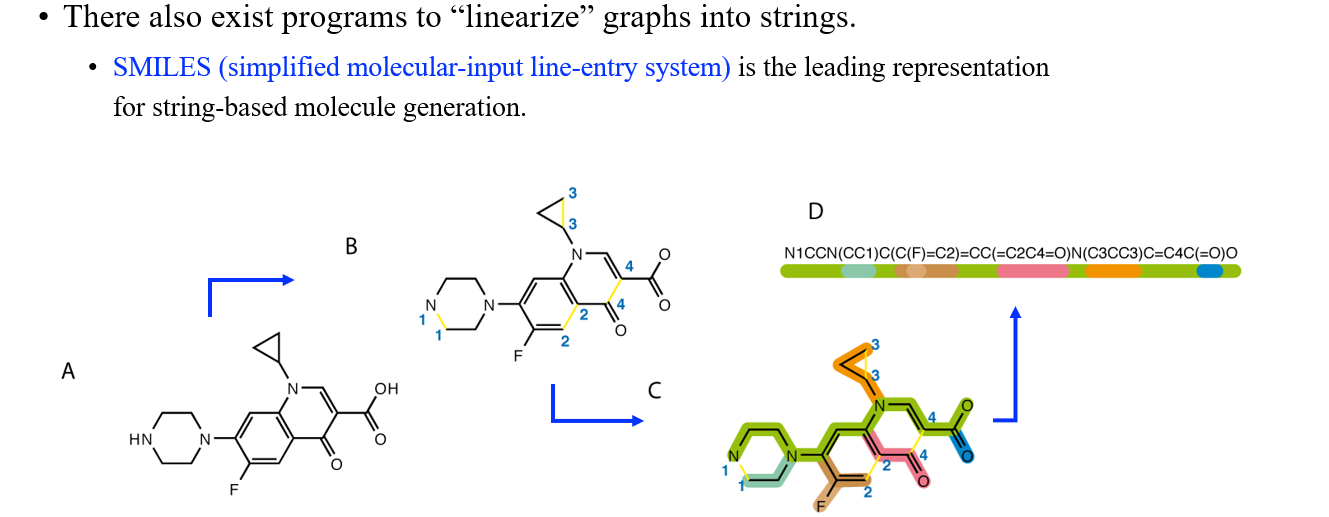그래서 molecule의 목적에 맞는 generation 방식으로 string-based graph generation이 존재하며, 사람들은 이를 SMILES (simplified molecular-input line-entry system)이라 부른다. 우리가 auto-regressive model을 이용해서 graph를 generation한다고 했을 때, 이미 다른 사람들이 text로부터 만들어 놓은 molecule을 이용할 수 있다. 여기서부터 SMILE의 아이디어는 시작되며 이는 매우 간단하다.
우리가 tree를 나타내고자 할 때 S-expression을 이용해서 표현할 수가 있다. 이는 tree를 표현할 때 bracket을 이용해서 sub-tree를 나타내는 등 tree 구조를 설명할 수 있는 대표적인 표현법 중 하나이다. SMILES은 어떻게 보면 S-expression의 수정된 버전으로 생각할 수 있다. 표현하고자 하는 molecule이 주어졌을 때, 사람들은 우선 spanning tree를 graph로부터 찾고자 할 것이다. 이러한 점에서 molecule을 생성한다고 하면 위와 같이 우선 spanning tree를 만들고나서 남은 residual edge들을 이어붙이는 식으로 graph를 완성하게 된다. 그리고 만약 indicator 1~4를 제거한다고하면 우리는 tree representation을 얻게 된다. 반대로 indicator를 남기게 된다면 전체 graph를 얻게되는 식이다.
Molecule은 특수한 형태의 graph이고, molecule 안에는 약간의 ring 구조를 포함하게 될 것이다. 약간의 ring 구조를 가진다는 것은 molecule graph를 tree를 사용해서 근사하려고 한다면, 약간의 edge가 남아있게 될 것이다. 왜냐하면 ring은 edge의 전체 숫자에서 spanning tree의 edge와의 차이만큼 존재하기 때문이다.
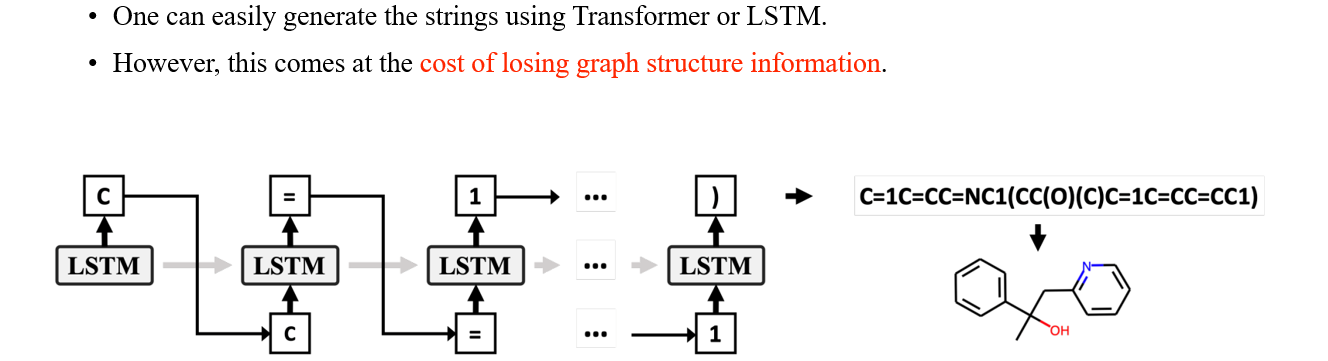
지금까지 본 SMILES 표기법이 deep learning의 관점에서 조금 이상해보일 수 있다. 아무래도 이러한 방식은 화학쪽 분야에서 molecule을 표현하는 방식이기 때문이다. 그래서 실제로 SMILES 표기법으로 molecule을 생성한다고 했을 때, text generative model을 이용해서 text를 만들어내는 식으로 molecule을 만들게 된다. Language 기반의 model로 molecule을 text 형태로 만들어냈다면 이후에는 특수한 decoder를 활용하여 이를 graph 형태의 molecule로 만들어내면 된다. String 기반의 generative model은 molecule을 만들어내기에 최적화 된 쉬운 방법 중 하나이다.
4) Tree-based Graph Generation
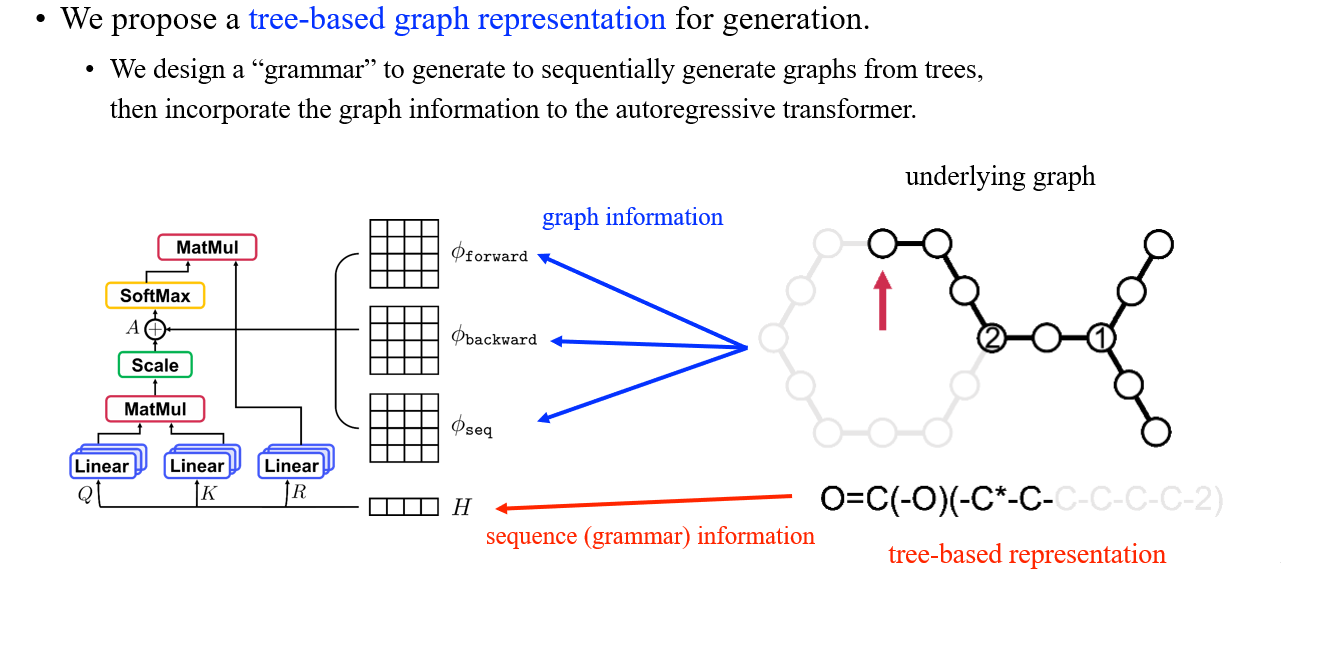지금까지 본 SMILES는 graph가 주어졌을 때 linear string으로 graph를 나타내는 방법이었다. 이를 좀 더 자세히 살펴보면 결국에는 graph를 일종의 tree로 변환하는 작업을 수행하게 된다. 특히 이러한 tree가 결국에는 text나 string으로 변환이 되었던 것이고, 이번에 살펴볼 tree-based graph generation에서는 tree 구조로부터 graph를 연속적으로 만들기 위한 grammar를 설계한다고 생각하면 된다. 여기서 tree는 원래의 molecular graph의 근사된 버전으로 볼 수가 있다. 결국 molecule graph와 tree를 양방향으로 변환할 수 있도록 grammar를 잘 설계해야하는 것이 tree-based graph generation의 핵심인 것이다. 기존의 text generation model보다 tree generation model이 원래의 graph 구조에 대한 더 많은 insight를 제공해줄 수 있다.
5) Tree-based Graph Generation
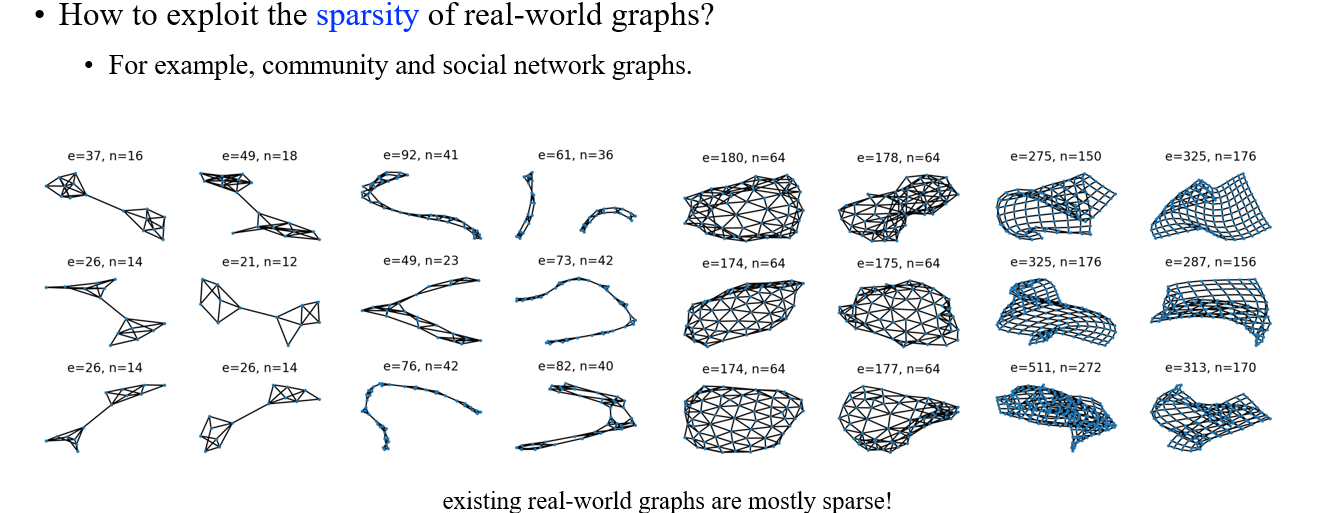Tree 기반의 방법이지만 graph의 특성들을 좀 더 clustering하는데 중점을 두는 Tree-based graph generation 방법도 존재한다. 예를 들어, 우리는 community나 social network는 하나의 큰 graph 속에 커다란 여러 sub-graph들이 존재한다는 prior knowledge를 어느정도 가지고 있다. 그리고 이렇게 큰 sub-graph들로 구성된 cluster 사이에는 edge가 거의 없다는 것도 어느정도 가정할 수 있다. 그래서 여기서 하고자 하는 방법은 이러한 사전지식들을 이용해서 더 효과적으로 graph를 생성하고자 하는 것이다.
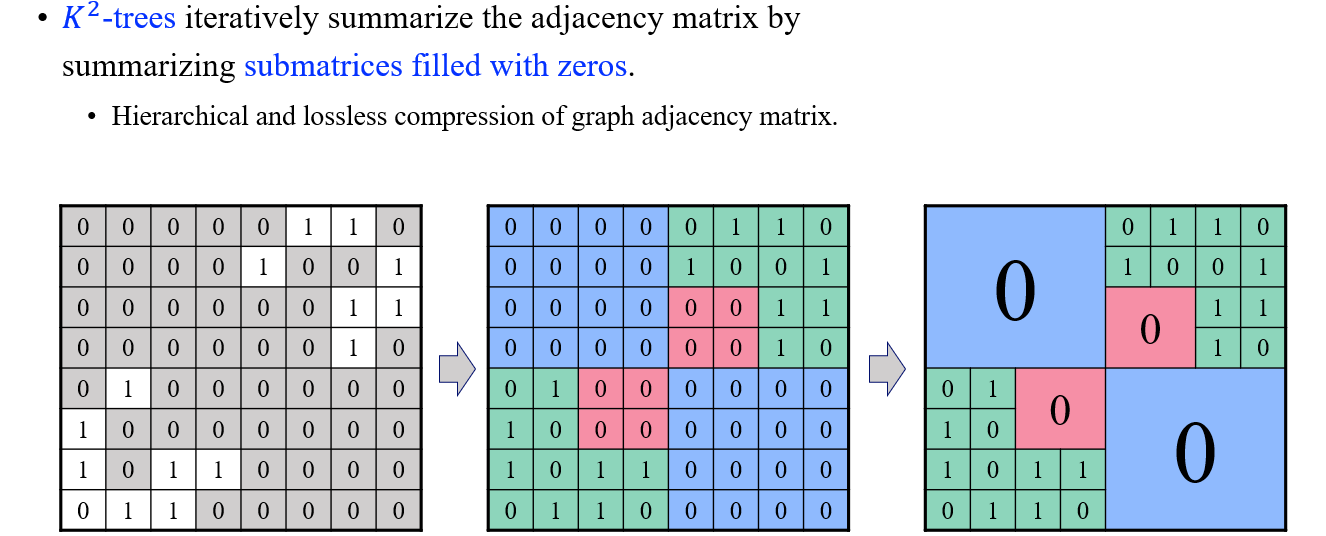이러한 가정 속에서 하나의 커다란 adjacency matrix 속에 0으로 이루어진 커다란 집단과 1이 어느정도 포함된 여러 집단들로 나눌 수가 있을 것이다. 그래서 하나의 element를 만들기보다는 조금 큰 단위의 집단을 한번에 생성할 수 있을 것이고, 이를 위해서 우리는 -Tree라는 것을 만들 수가 있다.
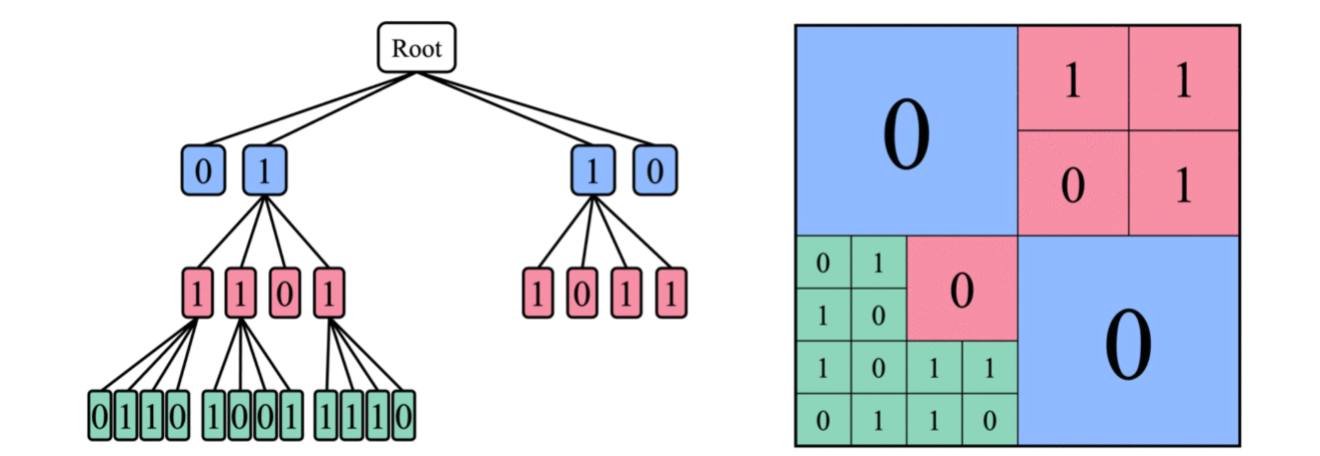-Tree는 matrix의 0으로부터 계층적 구조를 표현할 수 있다. 위와 같이 우측의 adjacency matrix와 같은 결과로 좌측과 같은 hierarchical tree를 구성할 수 있게 된다. 이러한 식으로 하나의 chunck를 만들게 되면 하나의 element를 만드는 과정보다 더욱 효과적으로 graph를 생성할 수 있게 된다.
Summary
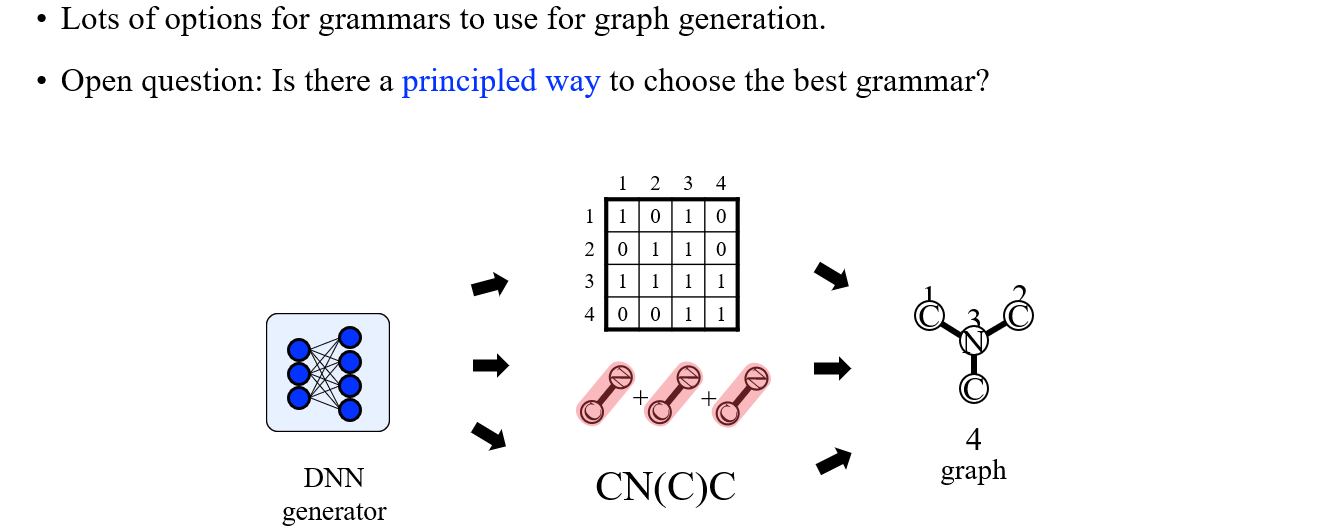지금까지 살펴본 여러 graph generation에 대한 grammer를 어떻게 얻을 수 있는지 알아보았다. 상황에 맞는 generation 방법을 적용하는 것이 더 나은 결과로 이어질 수 있을 것이다.
Research Direction 2: Probabilistic Frameworks
이번에 살펴볼 probabilistic framework는 이전에 보았던 auto-regressive model과는 다소 방향성이 좀 다르다. 하지만, 이러한 방법들도 최근에 사람들이 많은 관심을 가지고 연구되어지고 있다. 흔히 diffusion model이 여러 영역에서 성공적으로 결과물을 만들었기 때문에 graph 영역에서 또한 diffusion 연구가 활발히 진행되어지고 있다. 기본적으로 graph는 discrete한 구조를 가지고 있기 때문에 continuous한 framework인 diffusion이 graph에 잘 동작하도록 만드는 과정은 정말 최근에 와서야 조금씩 성공을 보이고 있다.
Autoregressive Models for Graphs
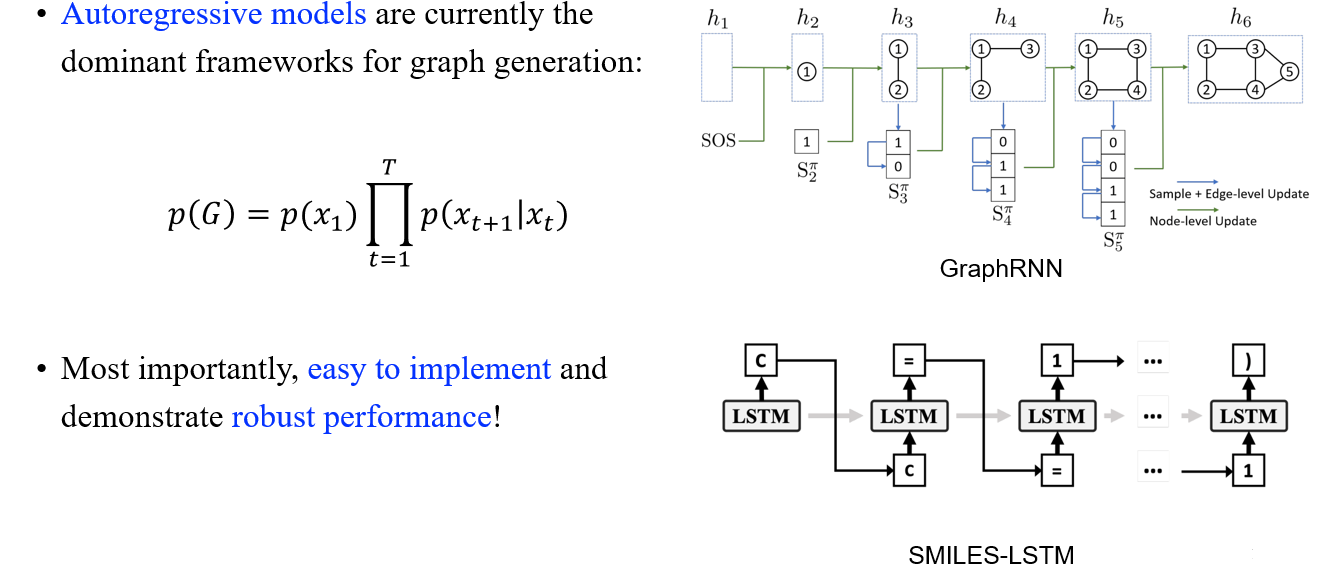Auto-regressive model들이 최근에 graph generation에서 상당히 좋은 결과들을 보여주고 있었지만, 한번에 하나의 element를 만든다는 점은 이 모델들이 느릴 수 밖에 없음을 보여주게 된다. 그래서 한번에 여러개의 element를 생성하는 과정이 있어야 더 빠르고 효과적으로 graph generation을 성공할 수 있도록 해준다.
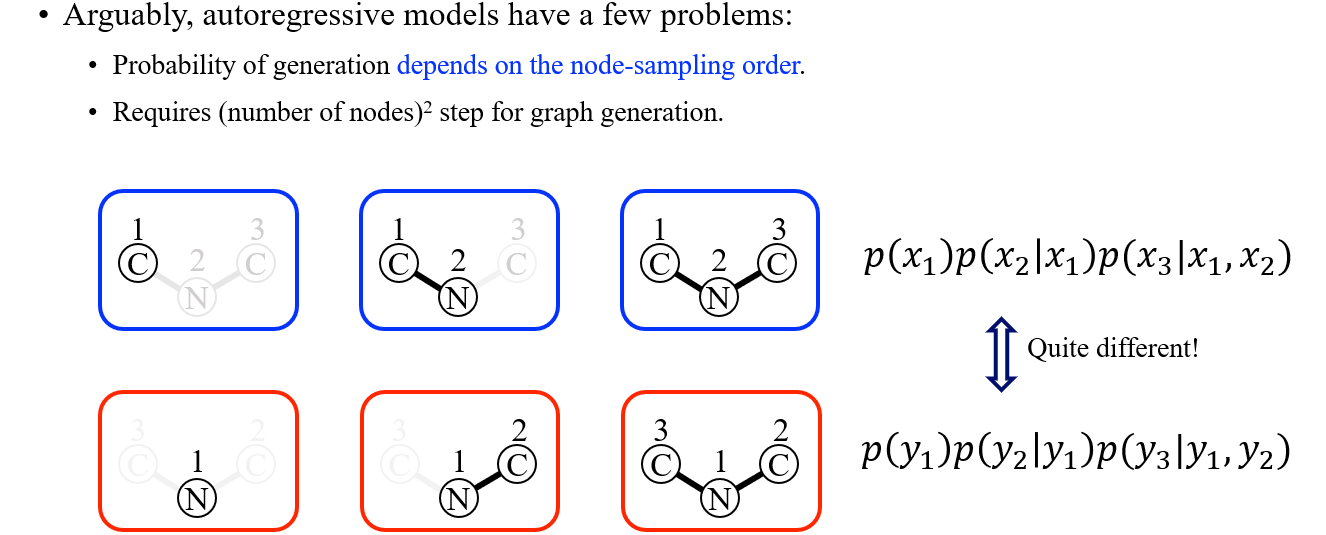처음부터 graph generation을 하고자 한다면, autoregressive model을 사용하는 것이 나쁜 선택이 아닐 것이다. 아무래도 tuning하는 과정이 어렵지도 않으며, 이에 따른 성능도 어느정도는 보장되어 있기 때문이다. 이 model들의 흥미로운 부분 중 하나로 graph의 permutation symmetry를 보장하지 않는다는 것이다. 예를 들어, 위와 같이 C-N-C 구조의 graph를 만든다고 했을 때, 똑같은 결과를 만들기 위해서 다양한 방법이 존재할 수 있다. 이렇게 auto-regressive model을 이용해서 graph를 생성하게 되면 만드는 순서에 따라 확률이 달라지게 된다.
Diffusion Models
이번에 알아볼 diffusion model의 경우 graph를 생성하는데 있어 node ordering과 관련이 없어 autoregressive model과는 다르게 permutation symmetry를 보장할 수 있게 된다. Diffusion model은 동시에 data의 모든 element를 generate할 수 있다. Image에서의 diffusion model은 image가 주어지면 noise를 조금씩 추가해서 완전한 noise distribution을 만들어주게 된다. 그리고 generative model을 이용해서 이로부터 다시 image를 만드는 과정을 학습하게 된다.
Diffusion Models for Graphs
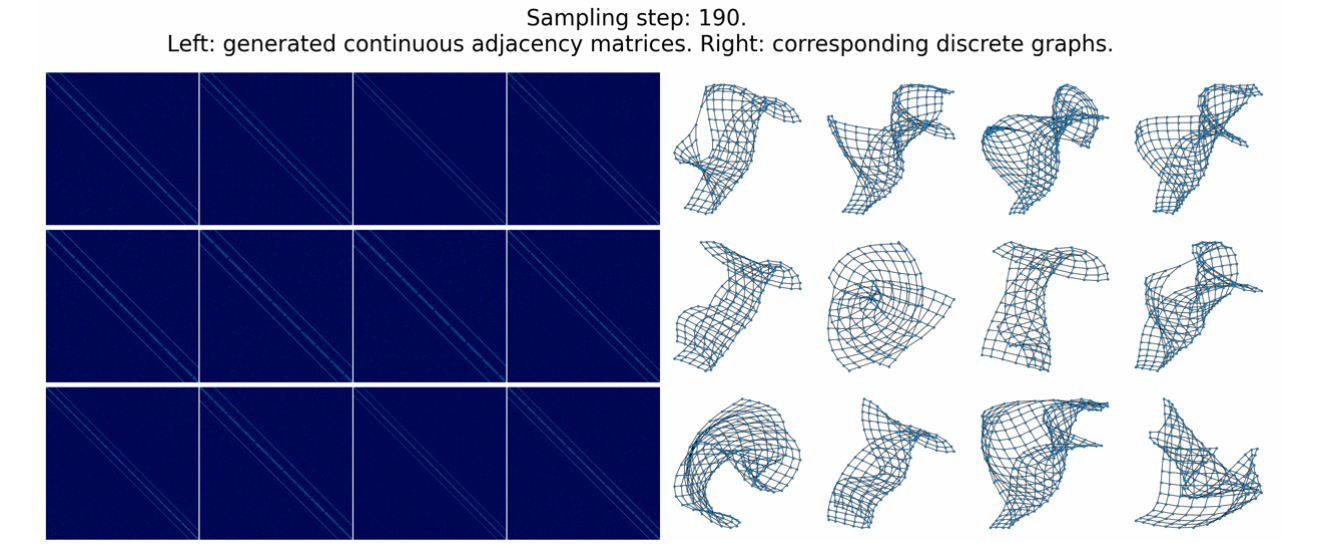Graph에서도 마찬가지로 adjacency matrix를 image와 같다고 생각하면 이해하기 쉬울 것이다. Noise distributino에서 시작해서 완전한 graph가 될 때까지 diffusion model을 학습시켜서 만들 수 있다.
Continuous Diffusion Models
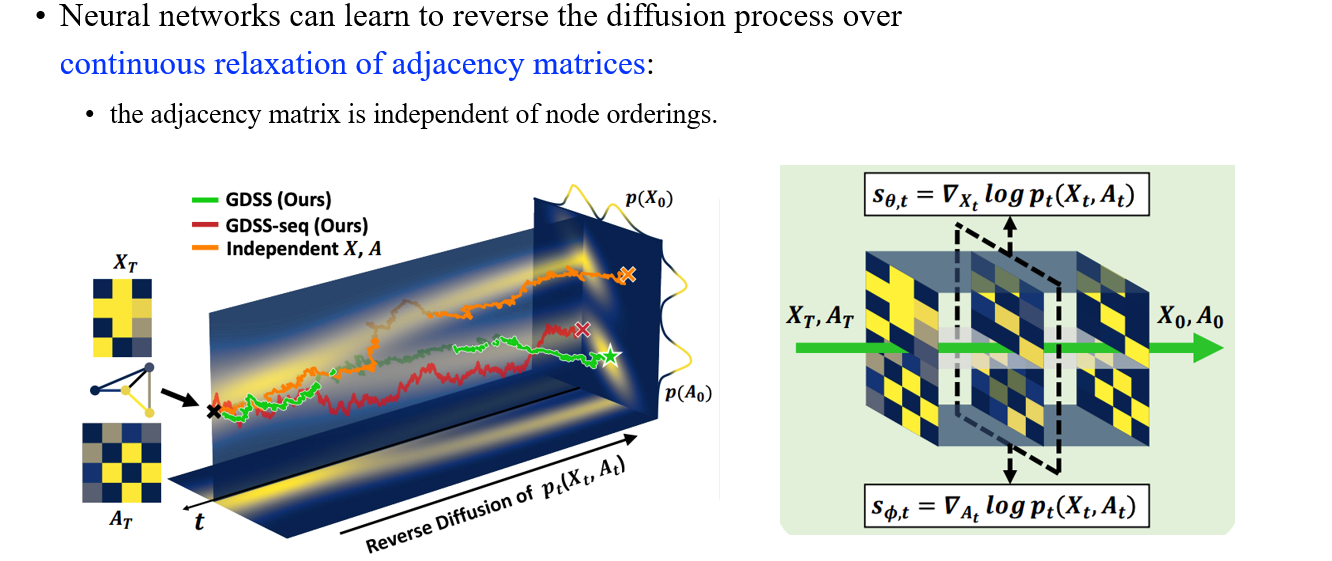Vertex의 크기만큼 adjacency matrix를 구성할 수 있고, continuous diffusion model을 이용하면 edge가 연속된 값으로 만들어지게 되는데 아무래도 원래 edge의 경우 binary 숫자로 존재성을 나타내기 때문에 thresholding을 거쳐서 graph를 만들 수 있게 된다.
Discrete Diffusion Models
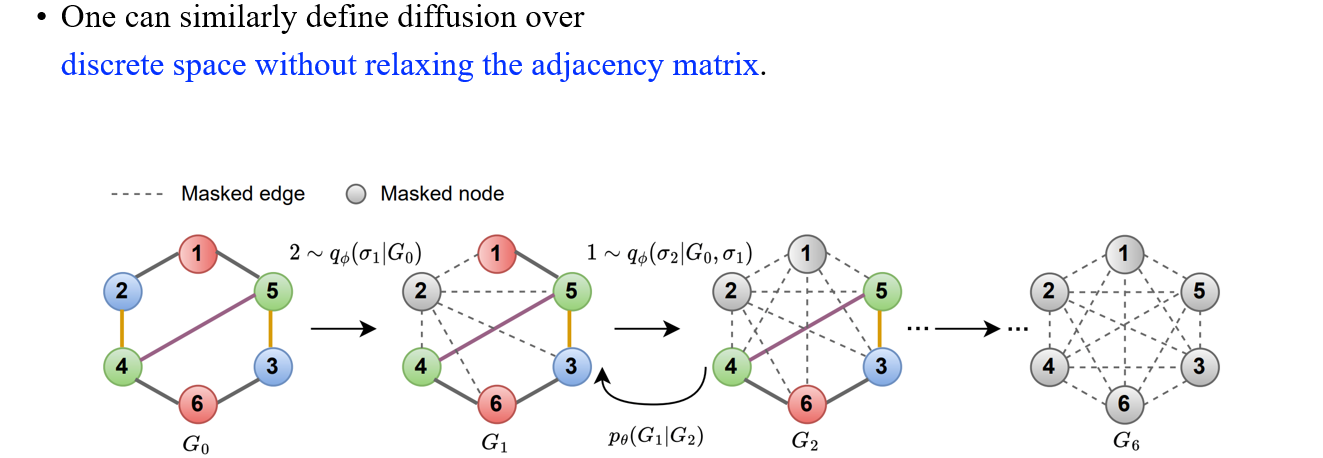이후에 사람들은 diffusion model을 discrete data에 적용하고자 많은 연구들을 진행해왔다. Diffusion model은 임의의 categorical data에 동작하도록 설계가 되어 있기 때문에 graph에 더 적합하도록 수정할 필요가 있었다.
Summary
요약하면 autoregressive model은 꽤 robust하면서 괜찮은 성능을 보여주었고, diffusion model은 autoregressive model에 비해서 성능적으로 아쉬운 부분이 많지만 얼마 안가서 분명 괜찮은 결과를 보여줄 것이다. 이 두가지 방법을 언제 활용하냐고 물어본다면 graph data가 text data와 같이 생겼다면 autoregressive model이 더 잘 동작할 것이고, graph data가 image data와 비슷하다면 diffusion model이 더 잘 동작할 것이다. 상황에 맞게 적절한 방법을 선택하고 적용해보면 될 것이다.
