[그래프 기계학습] Graph Neural Networks

Graph Neural Networks

지금까지는 graph를 처리하는 전통적인 algorithm들에 대해서 알아보았다. 이제부터는 graph를 처리하기 위한 deep learning 기반의 방법들에 대해서 알아보고자 한다. 이번에 알아볼 graph neural network (GNN)은 graph를 파악하는 neural network로 아이디어는 굉장히 간단하지만, 정말로 중요한 내용을 담고 있다.

우리는 graph가 주어졌을 때, 이 graph의 구조를 기반으로 non-linear transformation을 수행하는 multi layer로 구성된 vertex $v$에 대한 encoder를 설계하고자 한다. 특히, 이번에 알아보는 GNN의 경우에는 굉장히 high level에서의 아이디어를 직관적으로 이해할 수 있도록 하고자 한다. 그렇기 때문에 GNN의 가장 기본이 되는 구조에 집중해보고자 한다.

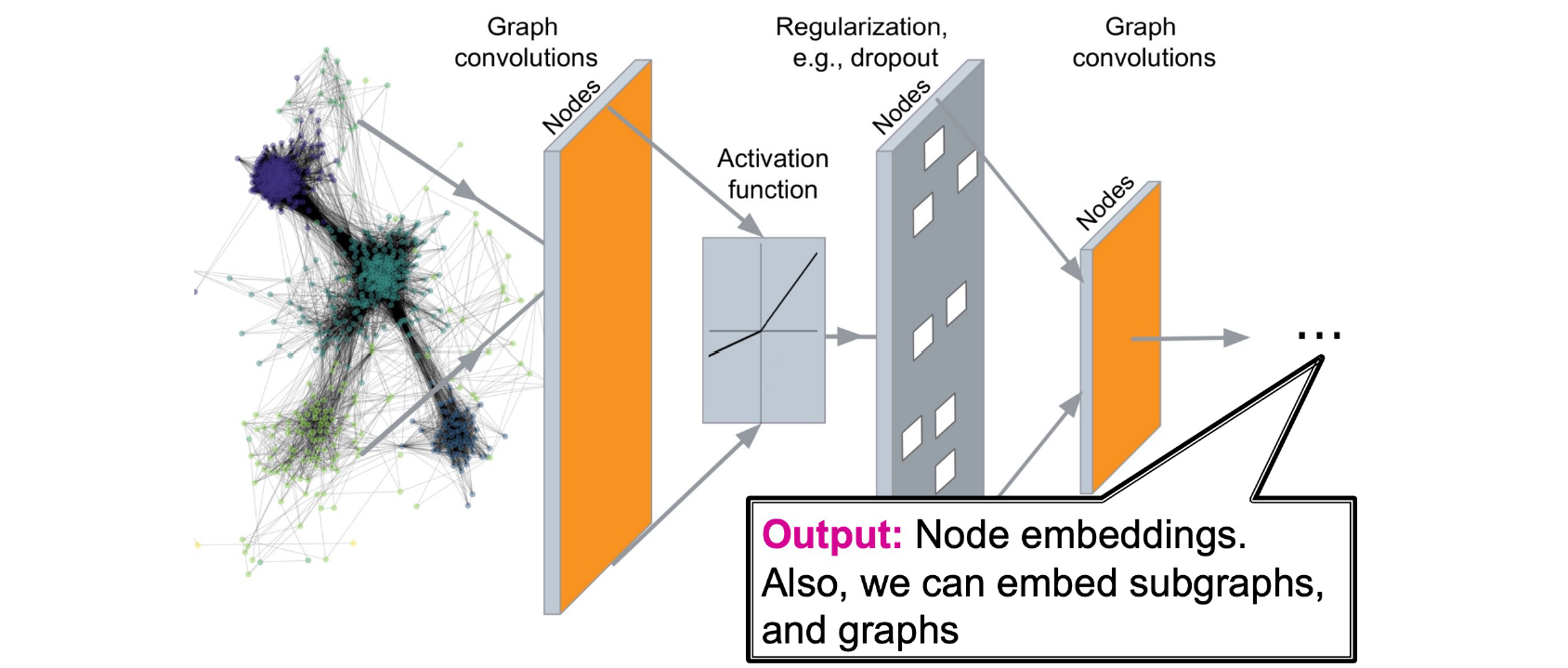다른 neural network와 마찬가지로 GNN도 여러 layer로 구성될 수 있고, 각각의 layer를 우리는 graph convolution을 수행하는 graph convolution layer로 부를 수 있다. 이후에 GNN을 CNN과 어떻게 다른지 비교해볼 것이며, 여기서 이야기할 수 있는건 GNN은 CNN의 generalization 버전인 셈이다. 즉, convolutional neural network를 graph로 확장했다고 볼 수 있다. 그래서 convolution operation을 graph에 수행했기 때문에 graph convolution이 되는 것이다. CNN이 image에 정의되었듯이 GNN은 graph에 정의가 되었고, graph에서의 vertex를 image에서의 pixel로 볼 수 있다. 결과적으로 GNN도 CNN처럼 convolution을 적용하고 activation을 적용할 수 있고, 추가적으로 dropout과 같은 regularization까지 적용시킬 수 있다. 이러한 과정들을 여러번 반복하면 결국 graph의 embedding을 output으로 얻을 수 있다.

Tasks on Networks

GNN을 사용해서 수행할 수 있는 대표적인 task로는 node classification이 있으면, 이는 graph가 주어졌을 때 각 node의 type을 맞춰야하는 task이다. 또 다른 task로는 link prediction이 있다. 예를 들어, 우리가 어떠한 social network가 있다고 했을 떄 두 사람 사이의 관계를 예측해보는 것이다. 이외에도 GNN을 사용하면 community detection이나 network similarity와 같은 다양한 task를 graph data에 대해서 수행할 수 있다. 여기서 community detection이나 network similairyt는 NP-hard problem들로 node classification이나 link prediction보다도 훨씬 어려운 task에 속하게 된다.

Modern ML Toolbox

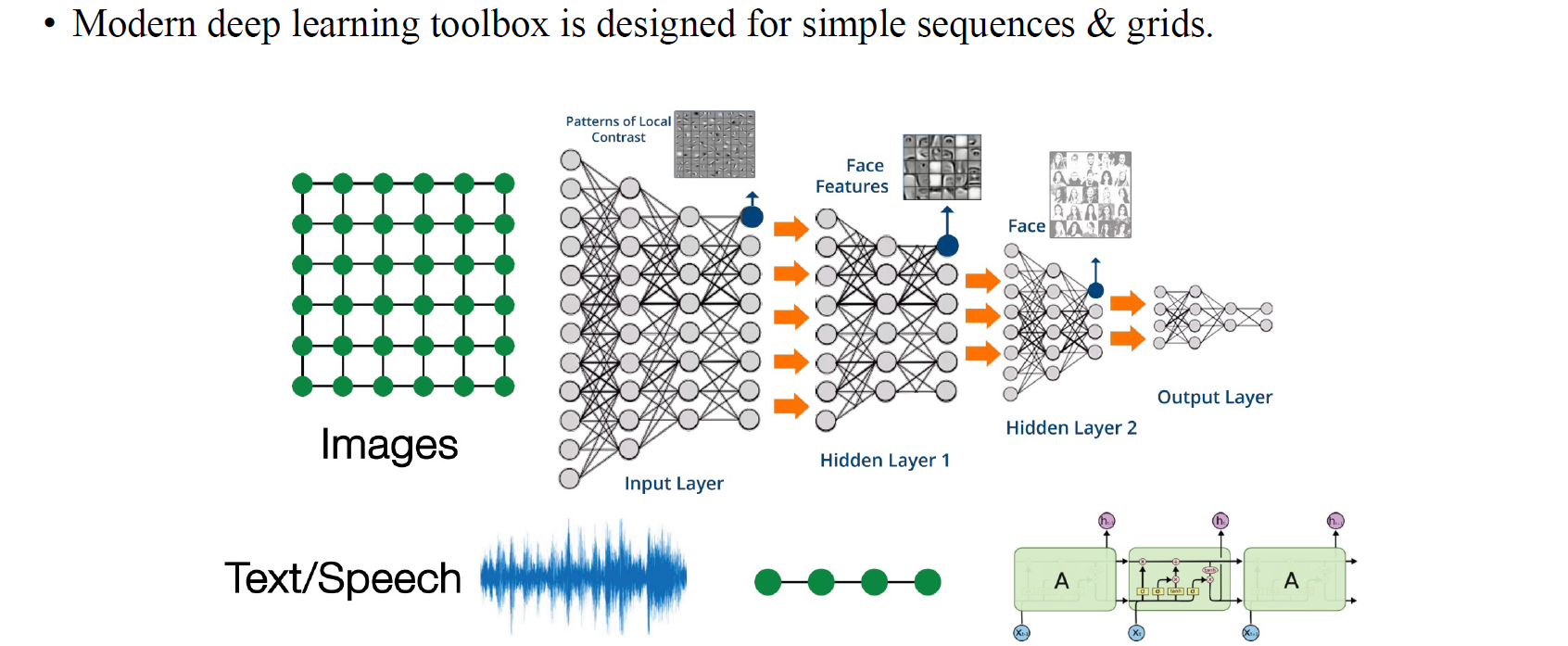Speech data나 text data와 같은 sequence data에 대해서 deep learning toolbox를 설게할 수 있다. 이는 image data와 같은 grid data도 마찬가지이다. 우리는 image에는 CNN, text에는 RNN이나 LSTM 등을 사용하면 되는걸 알고 있다.

Why is it Hard?

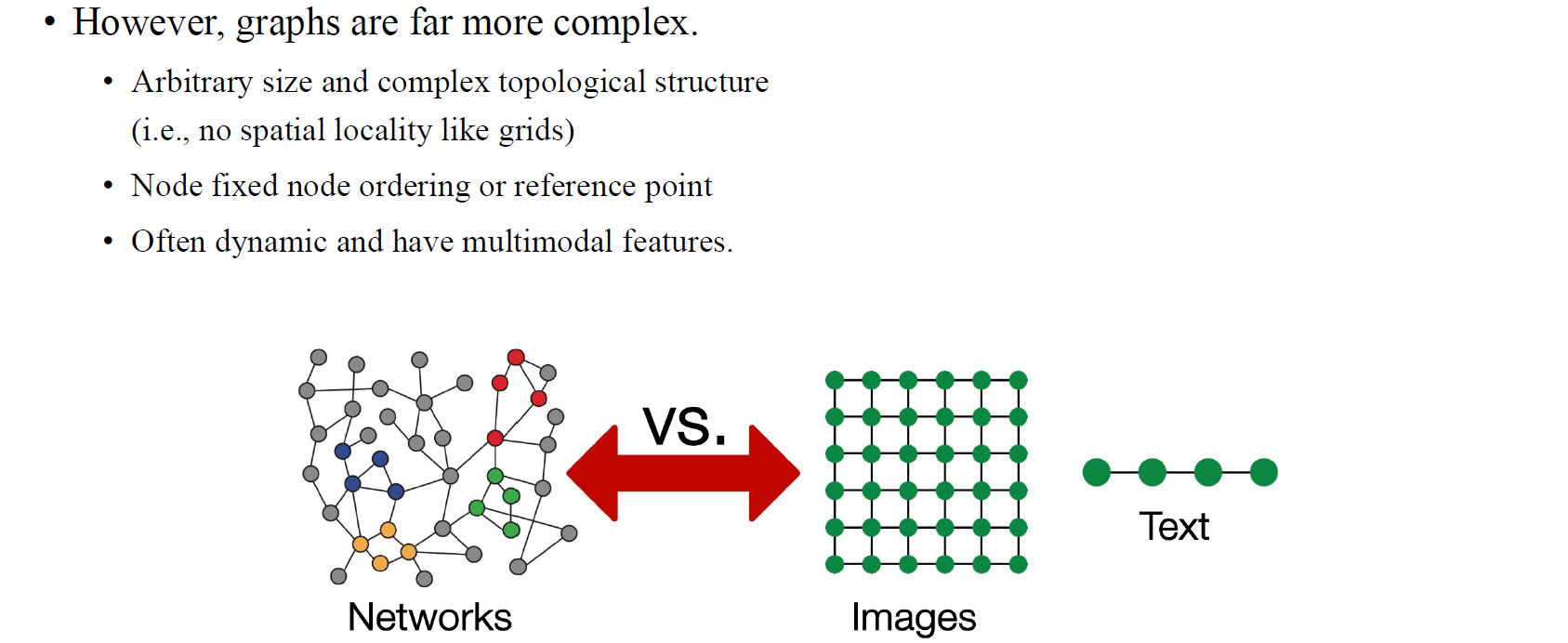하지만 이들에 비해서 GNN은 상대적으로 늦게 개발되고 발전해왔다. 왜냐하면 CNN이나 LSTM의 아이디러를 graph로 확장하는 것이 더 어렵기 때문이다. 그래서 graph에 맞게 deep learning framework를 개발하는 것이 어려운 이유 중 하나는 graph는 고정된 topological structure가 없기 때문이다. CNN으로 image를 처리한다고 했을 때 가정하는 것 중 하나가 image의 크기가 고정되어 있다는 점이다. 하지만, graph는 고정된 connectivity도 없고 고정된 형태로 존재하지도 않기 때문에 GNN을 설계하기가 굉장히 까다로울 수 있다. 이러한 이유 때문에 GNN은 flexible한 성질을 가지고 있어야 한다.

Text의 경우에 좌측에서 우측으로 진행되는 sequential한 형태를 지니고 있다. 그래서 text를 line graph로 표현이 가능하여 일관된 방식으로 특정 순서를 매길 수가 있다. Image도 마찬가지로 좌측에서 우측으로, 위에서 아래로 가는 특정한 규칙이 존재한다. 하지만 graph는 이렇다할 순서를 매기기가 어렵다. 물론 순서를 매기려고 노력해볼 수는 있다. 하지만 어떠한 순서와 규칙으로 순서를 매길지에 대해서 이 또한 의문일 수 있다. 가령, social network만 생각해보더라도 수시로 정보가 바뀌는 성질을 지니고 있어서 이에 따른 모델을 설계하는데 어려움이 존재한다. 그래서 이미 존재하는 framework로 이렇게 동적으로 변하는 graph를 처리하는데는 어려움이 있다.

GNNs in a Nutshell

그래서 GNN은 이러한 문제들을 해결하기 위해서 설계가 되었다. GNN을 설명하는 방법들이 여러가지 존재하지만, 가장 간단한 방법으로 local network로 구성된 여러 layer를 stacking함으로써 GNN을 설명하고자 한다.

Setup

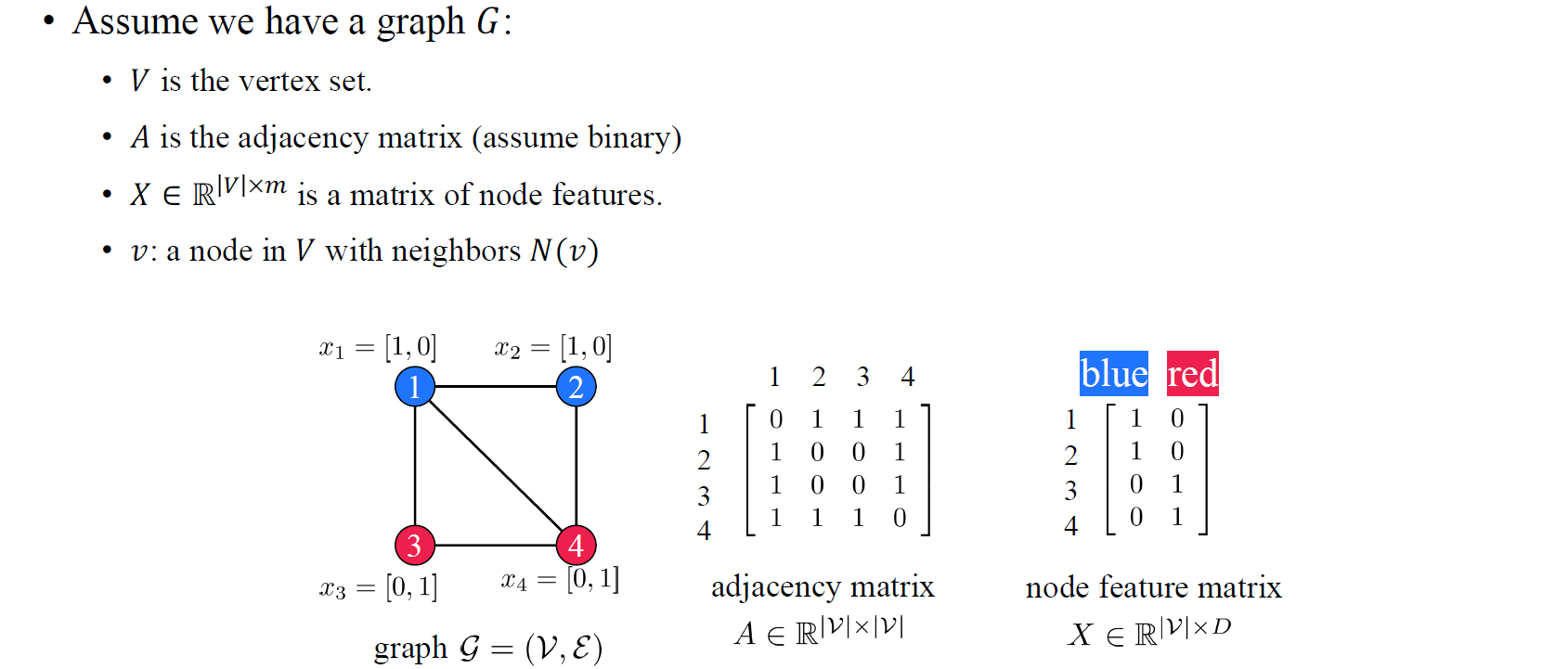이를 설명하고자 우리는 간단한 구조의 graph $G$를 가정하고 시작하고자 한다. $V$는 vertex set, $A$는 adjacency matrix이며, $G$는 undirected graph로 edge의 방향성이 없다는 가정을 할 것이다. 특히 undirected graph의 경우 adjacency matrix는 symmetric하게 구성되어 1인 위치에서의 두 vertex는 연결되었음을 설명하게 된다. 추가로 node feature matrix $X$는 vertex의 크기와 feature의 차원으로 matrix가 형성되며, 각 vertex의 feature 정보를 담고 있다. 위의 예시에서는 각 vertex의 색깔 정보를 feature로 하여 node feature matrix를 형성할 수 있게 된다. 그리고 특정 vertex $v$의 이웃한 vertex들을 우리는 $N(v)$로 정의할 수 있다. 정의는 하기 나름이며, 이렇게 정의하는 방식이 일반적이고 수학적으로 설명하기에도 용이한 편이다.

A Naive Approach

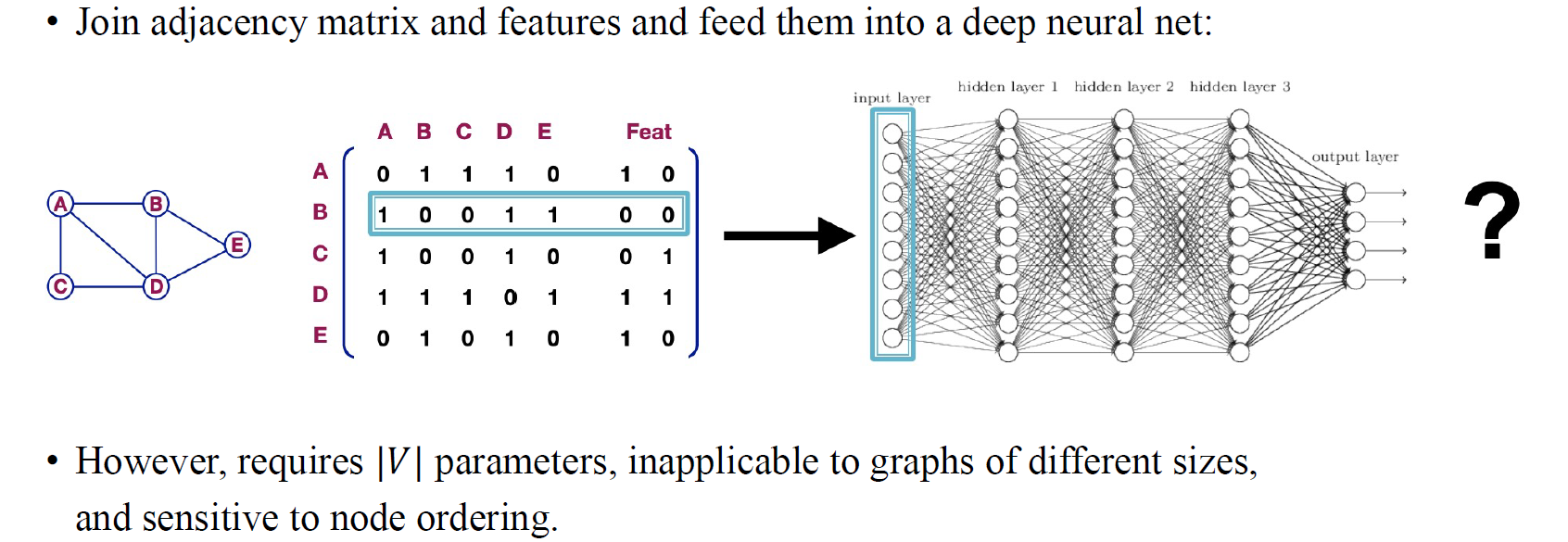본격적으로 GNN에 들어가기 앞서 가장 naive한 방식으로 기존의 MLP를 사용해서 adjacency matrix를 파악해보고자 한다. Graph가 주어졌을 때 컴퓨터는 graph를 온전히 받아들이지 못한다. 그래서 graph를 matrix 형태로 처리해주는 과정이 필요하고, adjacency matrix는 graph의 구조를 컴퓨터가 받아들일 수 있도록 해준다. 그래서 우리는 adjacency matrix와 node feature matrix를 concat해서 컴퓨터가 인식할 수 있도록 하고자 한다. 이렇게 형성된 data matrix를 deep neural network에 fitting시키고자 한다.

하지만 이러한 방식은 vertex에 비례하여 늘어나는 parameter 때문에 사실 좋은 방식이 아닐 것이다. MLP의 경우 전체 graph의 vertex의 수만큼 neuron이 필요할 것이다. 하지만 이렇게 되면 graph의 vertex의 수가 달라질 때마다 MLP 구조가 새롭게 정의되어야 해서 neural network의 구조가 계속해서 바뀌게 될 것이다. 이러한 비효율성 때문에 MLP를 사용하는데 문제가 있으며, 그렇기 때문에 transformer가 만들어지는 계기가 되었을지도 모른다. 사람들은 MLP를 크기가 변하는 sequence data에 맞게 사용하고 싶었기에 transformer가 등장하였고, 이와 같은 맥락으로 유동적인 graph에 맞게 사용하고자 GNN이 등장하였다고 볼 수도 있다.

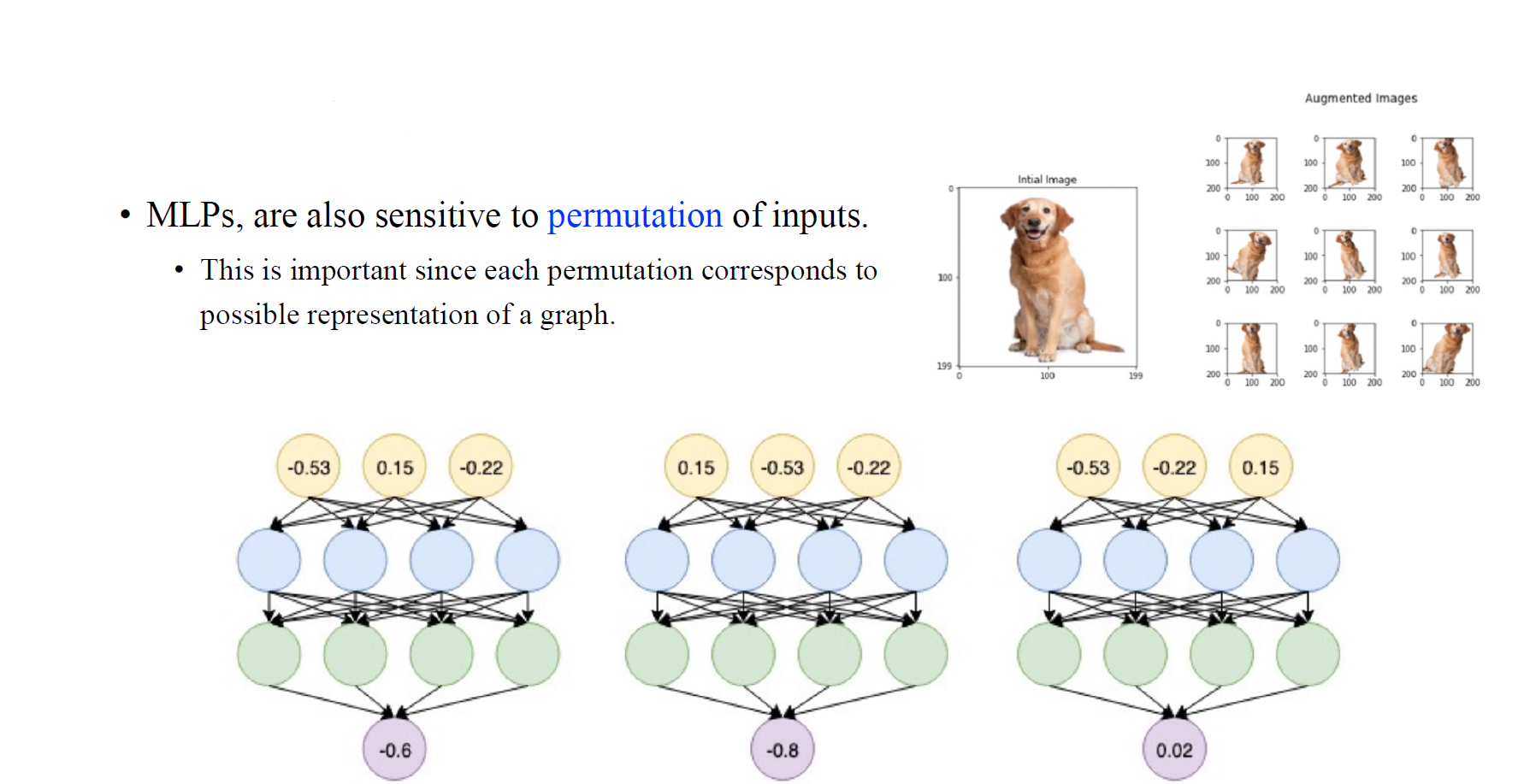MLP 사용의 또 다른 문제로는 input의 permutation에 민감할 수 있다는 점이다. 우리는 하나의 graph를 파악하는데 여러 방법들을 사용할 수 있다. 비록 동일한 graph일지라도 이는 서로 다른 adjacency matrix에 의해서 설명될 수 있다. 아무래도 graph에 있는 모든 vertex가 어떠한 순서로 동일하게 설명되기 보다는 다양하게 표현될 수 있기 때문이다. 이러한 과정은 어떻게 보면 image augmentation과 동일한 맥락으로 이해할 수 있다. 예를 들어, 비록 하나의 image에서 특정 강아지가 동일한 정체성을 가지고 있더라도 augmentation을 통해서 다양하게 표현될 수 있을 것이다. 이러한 맥락에서 graph에서도 여러 permutation 속에서도 하나의 graph로 설명될 수 있어야 한다.

그래서 GNN을 설계할 때 고려해야하는 부분으로 graph마다 서로 다른 크기를 가진다는 점과 node들의 permutation 속에서도 invariance를 보존해야 한다는 점이다. 그리고 서로 다른 adjacency matrix라도 하나의 graph를 설명한다는 부분을 간과해서는 안되는 것이다. 즉, vertex의 순서가 바뀌더라도 output의 결과가 바뀌는 것을 허용해서는 안될 것이다.

Idea: Convolutional Networks

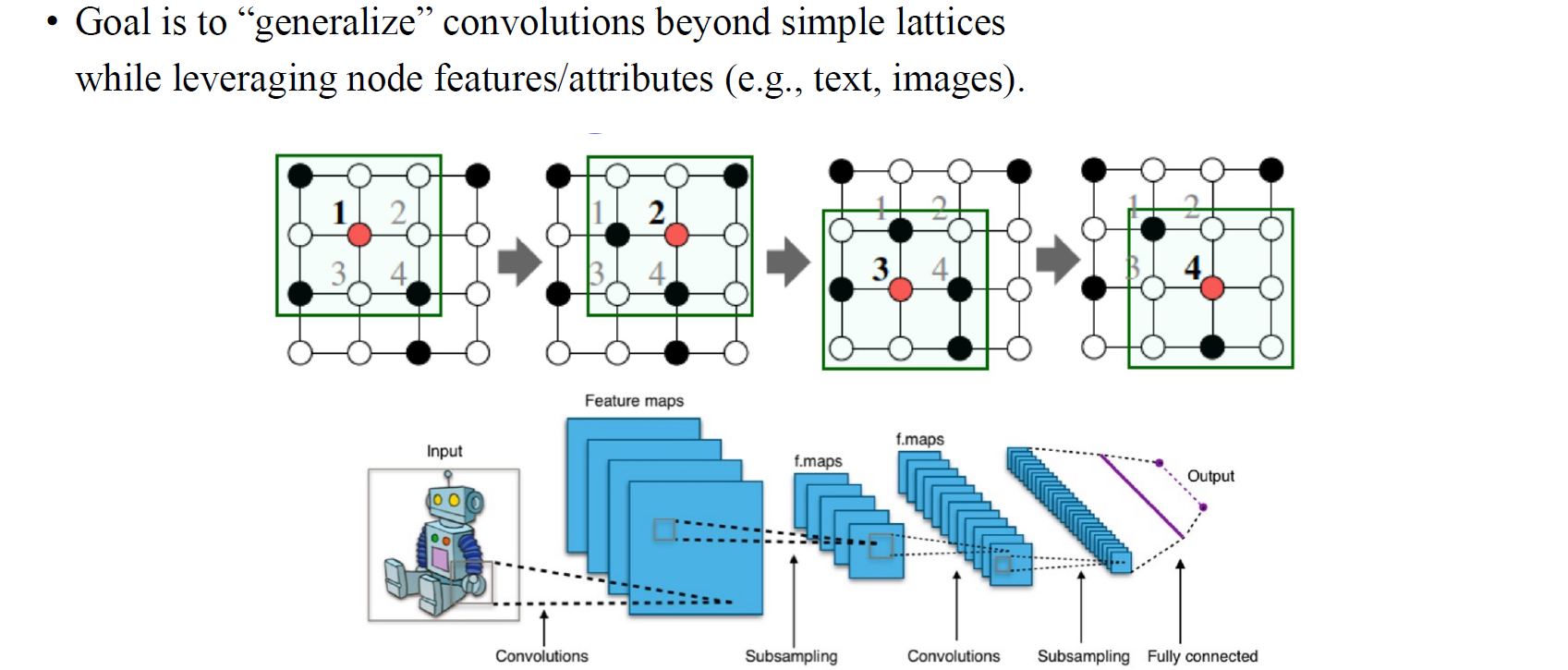우리가 결국 하고자 하는 아이디어는 convolutional neural network의 개념을 generalization하여 graph neural network를 만들고자 하는 것이다. 앞서 이야기했듯이 CNN과 GNN 사이에는 어떠한 연관성들이 존재한다. CNN은 image에 translation invariant한 성질을 지니고 있다. Image를 조금 움직이더라도 output이 바뀌지 않아야한다는 가정이 존재한다. GNN도 마찬가지로 vertex들을 permute하더라도 그 결과가 바뀌지 않아야하는 보장이 있어야 한다. 이렇듯 CNN과 GNN 모두 input이 어떠한 방식으로 바뀌든 상관없이 output이 바뀌지 않아야한다는 제약조건이 강하게 존재한다.

하지만 GNN으로 generalization하는 과정은 그리 쉽지만은 않다. CNN은 2D image에 대해서 특정 크기를 가지는 filter를 이용해 고정된 convolution을 수행하게 된다. 우리는 filter라는 도구를 이용해서 고정된 vertex (pixel)에 대해서 손쉽게 convolution 연산을 수행하여 이웃 vertex들의 정보를 모으게 된다. 그리고 filter에는 그 크기에 맞게 학습해야하는 parameter들이 존재한다. Filter를 만들면 image 전체를 돌아다니면서 parameter를 업데이트하게 된다. 여기서 CNN의 문제는 각각의 이웃 vertex들에 대해 서로 다른 parameter를 할당한다는 것이다.

Real-World Graphs

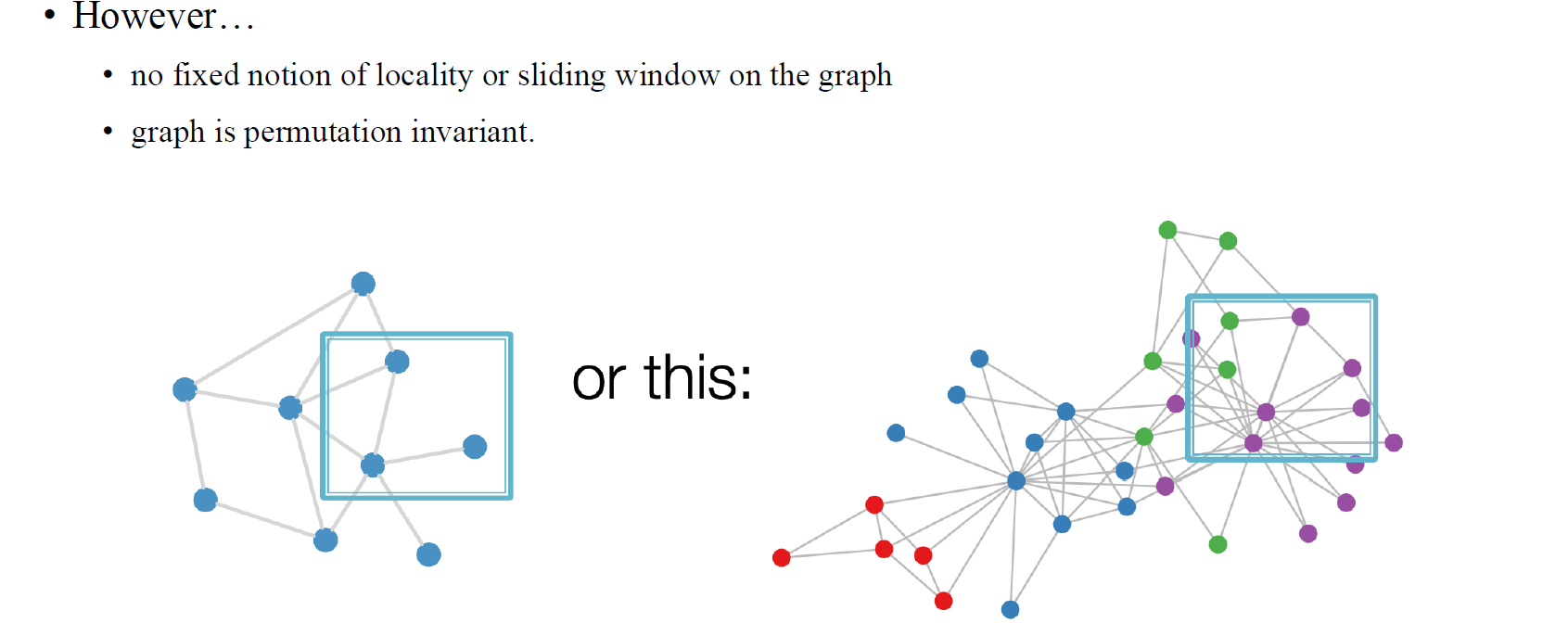반면, GNN은 이러한 방식과는 좀 다르게 convolution을 수행하게 된다. CNN의 경우 image의 특성상 동일한 크기의 filter로 고정된 이웃들을 보게 되지만, GNN의 경우 각각의 vertex마다 이웃의 개수가 전부 다르기 때문에 이러한 방식을 그대로 적용하는데 한계가 존재한다. 그래서 GNN을 설계하는 경우 기존의 CNN보다 좀 더 유연한 방식으로 설계해야만 할 것이다. 자세한 내용은 이후 graph convolutional network (GCN)에 대해 알아가면서 이야기하고자 한다.

Permutation Invariance and Equivariance

GNN의 convolution을 수식적으로 접근하기 이전에 permutation invariance와 equivariance problem들에 대해서 자세하게 알아보고자 한다.

Permutation

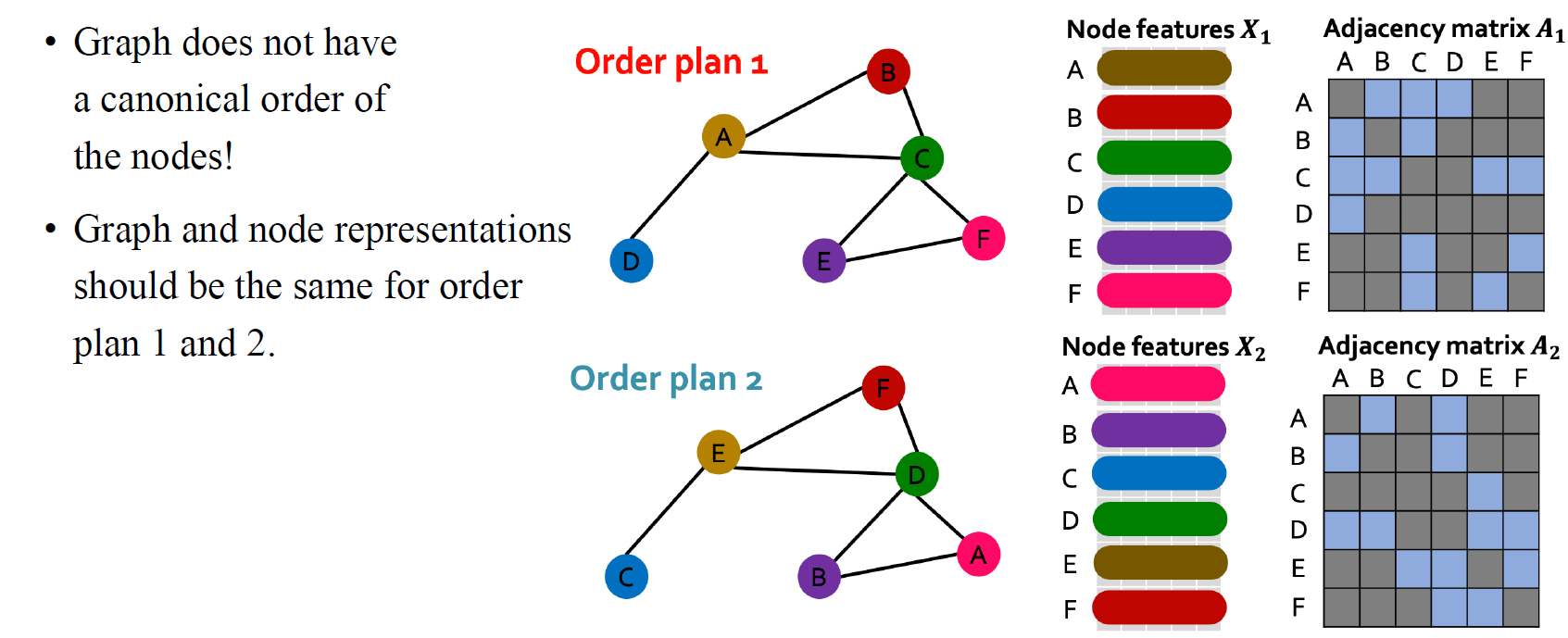Permutation은 vertex들의 순서를 바꾸는 행위를 이야기한다. 그러나 만약 우리가 좀 더 형식적인걸 원한다면 permutation을 graph나 어떤 object에 적용할 수 있는 transformation으로 정의할 수도 있을 것이다. 우리가 permutation을 다뤄야하는 이유는 graph 자체로 모든 node에 대해서 어떠한 canonical ordering이 없기 때문이다. 하지만 우리는 특정 graph를 설명할 수 있는 어떠한 순서를 정해서 컴퓨터에 입력시켜줘야만 한다. 그렇게 adjacency matrix를 만드는 것도 방법일 수가 있는 것이다.

만약 우리가 위와 같이 같은 그래프이지만 순서가 서로 다른 order plan1과 order plan2가 있다고 가정해보자. 그러면 이에 따라 각각 다른 node feature $X_1$과 $X_2$를 얻을 것이다. 아무래도 node feature는 ordering에 의존적이기 때문이다. 마찬가지로 각각에 대응되는 adjacency matrix $A_1$과 $A_2$도 얻을 것이다.

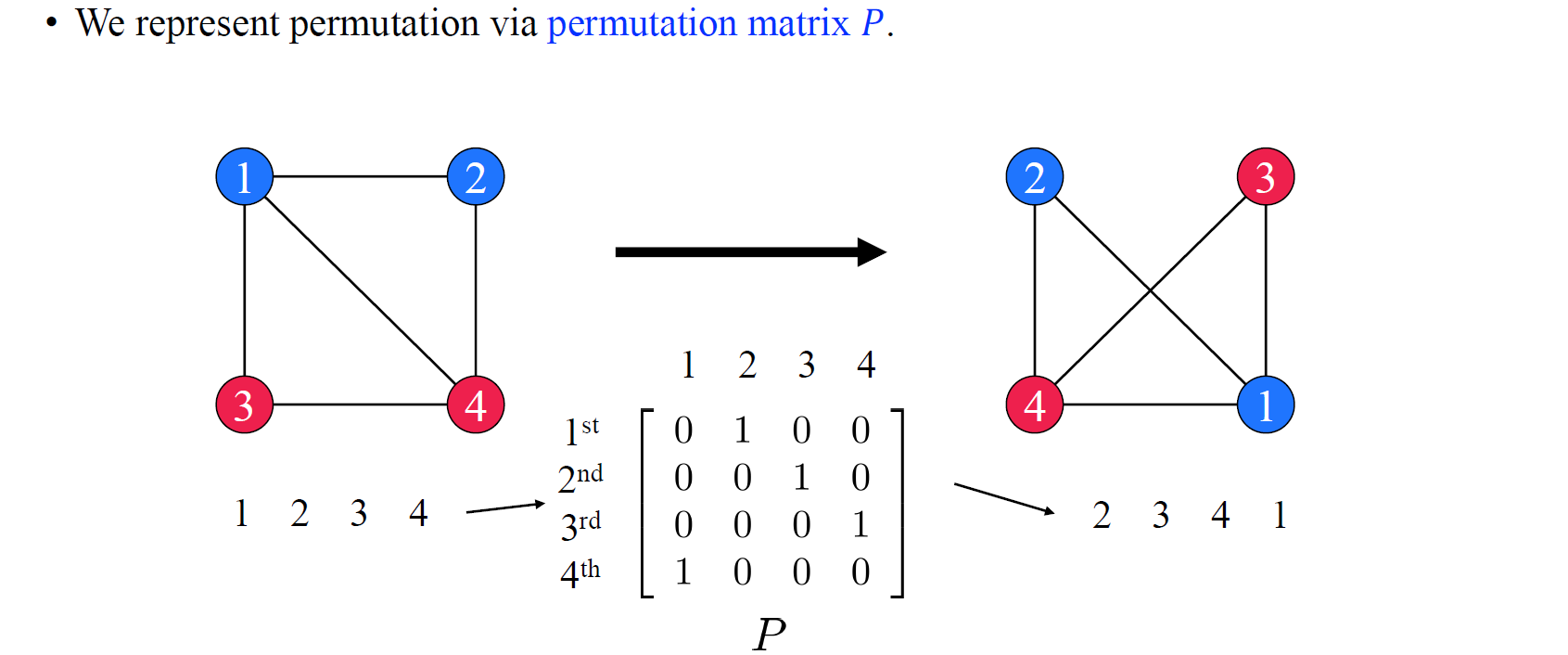여기서 우리는 permutation을 matrix multiplication으로 표현하기를 원한다. 그리고 이는 permutation matrix $P$와 관련된 multiplication으로 설명할 수 있게 된다. 우리는 permutation matrix를 좌측의 순서(1234)에서 우측의 순서(2341)로 바꿔주는 식으로 정의할 것이다. 1을 2로 바꾸고자 (1,2)의 위치에 1을 넣고 2를 3으로 바꾸고자 (2,3)에 1을 넣는 식으로 $P$를 binary matrix로 구성해서 ordering을 정할 수 있게 된다.

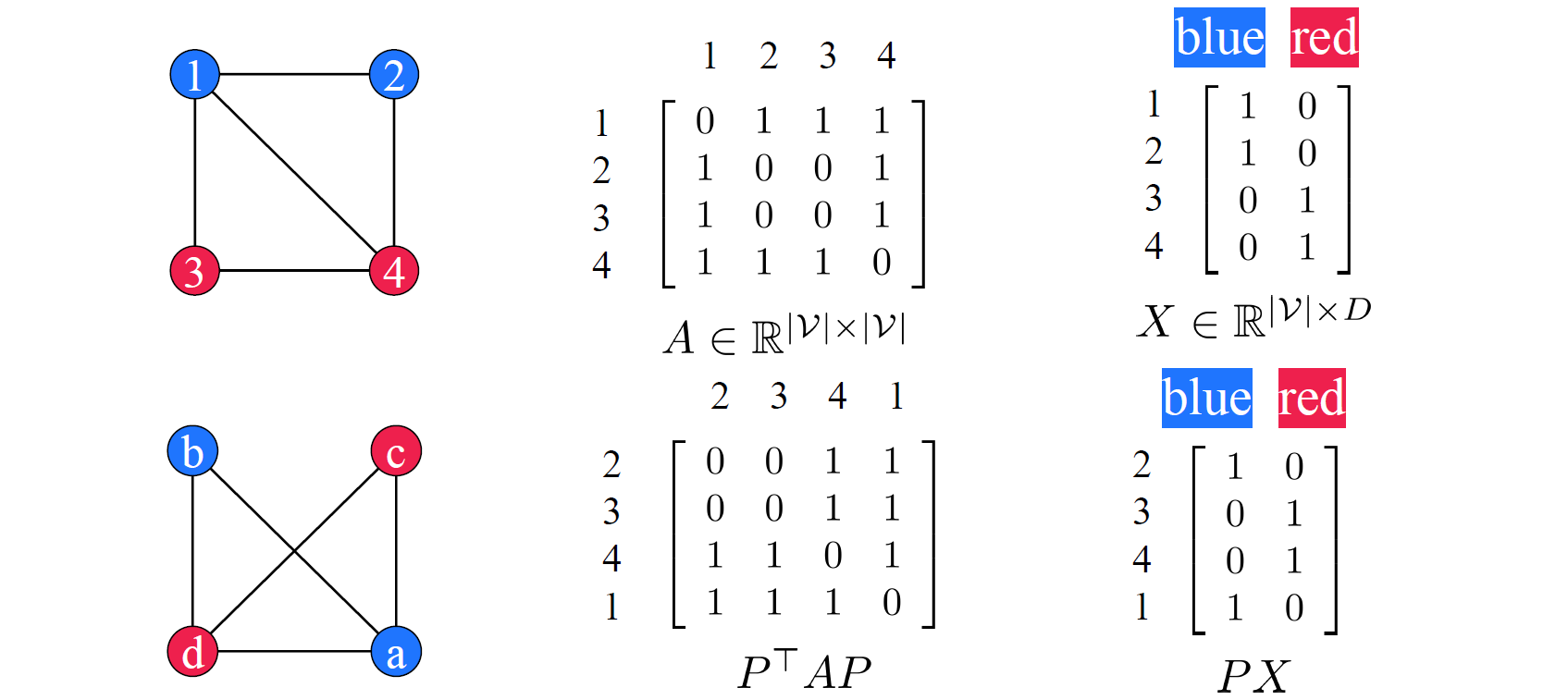그러면 이제 좌측과 같이 1234의 graph 하나와 bcda의 graph 하나가 있다고 해보자. 여기서 bcda는 2341 순서를 가지는 graph로 생각해도 된다. 그러면 각각의 graph를 설명하는 adjacency matrix가 중간과 같이 존재할 것이다. 여기서 우선 상단의 adjacency graph가 있다고 있고, 1234를 2341로 바꿔주는 permutation matrix $P$가 있다고 해보자. 만약 어떤 graph가 특정 permuation으로 변환될 수 있다면, 우리는 기존의 adjacency 양쪽에 permuation matrix를 곱해서 해당 transformation을 수행할 수 있을 것이다. 아래와 같이 $P$를 $A$에 곱해서 permutation을 수행한 것인데, 결국 좌측 $P$의 역할이 permutation을 어떻게 할지 결정하게 되는 수단이 되는 것이고, 우측 $P$의 역할이 adjacency의 column을 permuation해서 symmetric하게 만들어주게 된다. 이렇게 좌측과 우측에 $P$를 곱해야만 하는 것이고, 이로 인하여 우리는 새로운 adjacency matrix를 아래와 같이 얻을 수 있는 것이다. 마찬가지로 node feature $X$에도 $P$를 곱해서 permuation을 시켜줄 수 있다.

Permutation Invariance

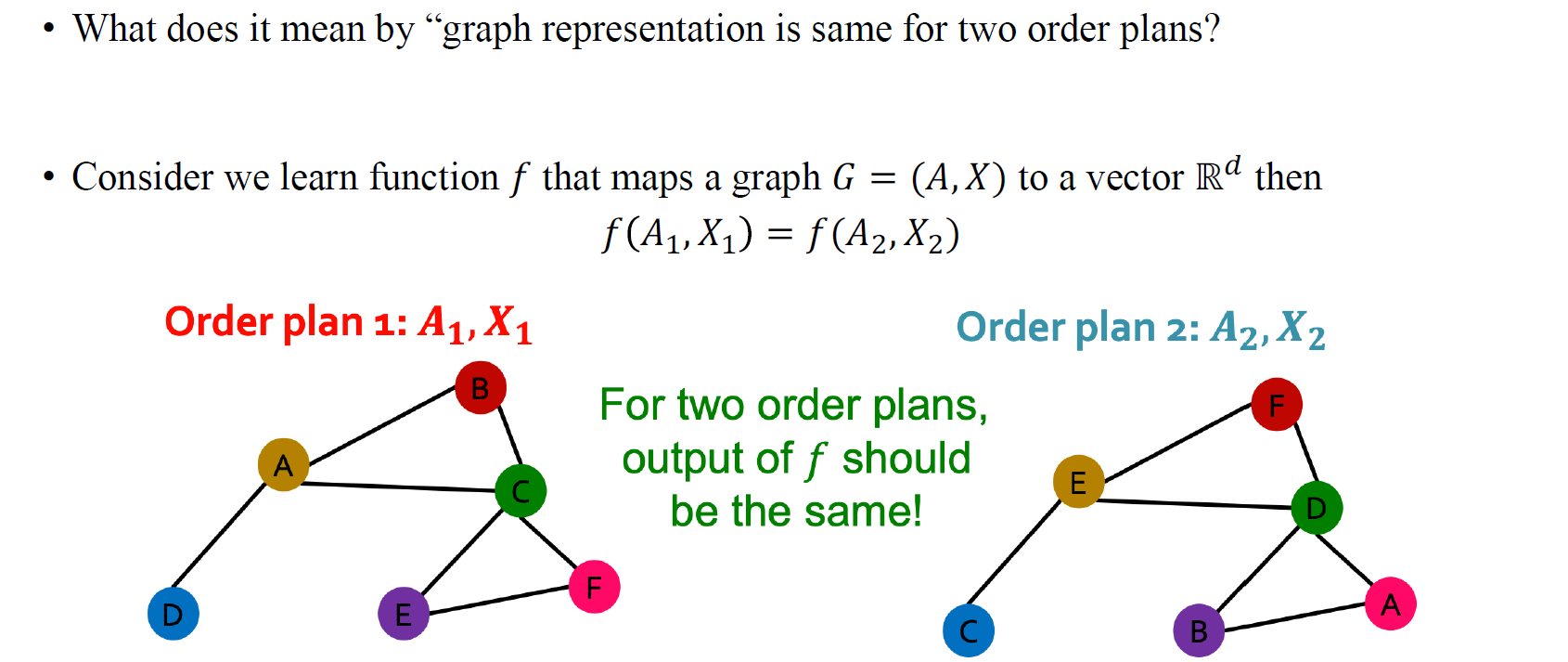지금까지 우리는 permutation operation을 graph에서 어떻게 할지에 대해서 알아보았고, 특히 adjacency matrix와 node feature matrix에 대해서 동작하는 과정을 보았다. 만약 우리가 서로 다른 order plan에 대해서 graph representation이 동일하도록 공식화하고자 한다면, 즉, 만약 permutation과 관련하여 2가지 representation이 존재하고 있다면, 결국 특정 function(GNN)의 output이 이들을 input으로 하였을 때 동일해야만 할 것이다. 우리는 이를 permutation invariance로 정의한다.

이를 위와같이 수식으로 정의하면, 만약에 $f(A,X)$가 $f(PAP^T,PX)$와 동일하다면, 우리는 $f$라는 특정 함수가 permutation-invariant하다고 할 것이다. 이는 굉장히 유용한 개념이다. 왜냐하면 비록 graph가 다르게 표현되어 있더라도, 특정 함수는 여전히 동일한 output을 만들어내기 때문이다.

Permutation Equivariance

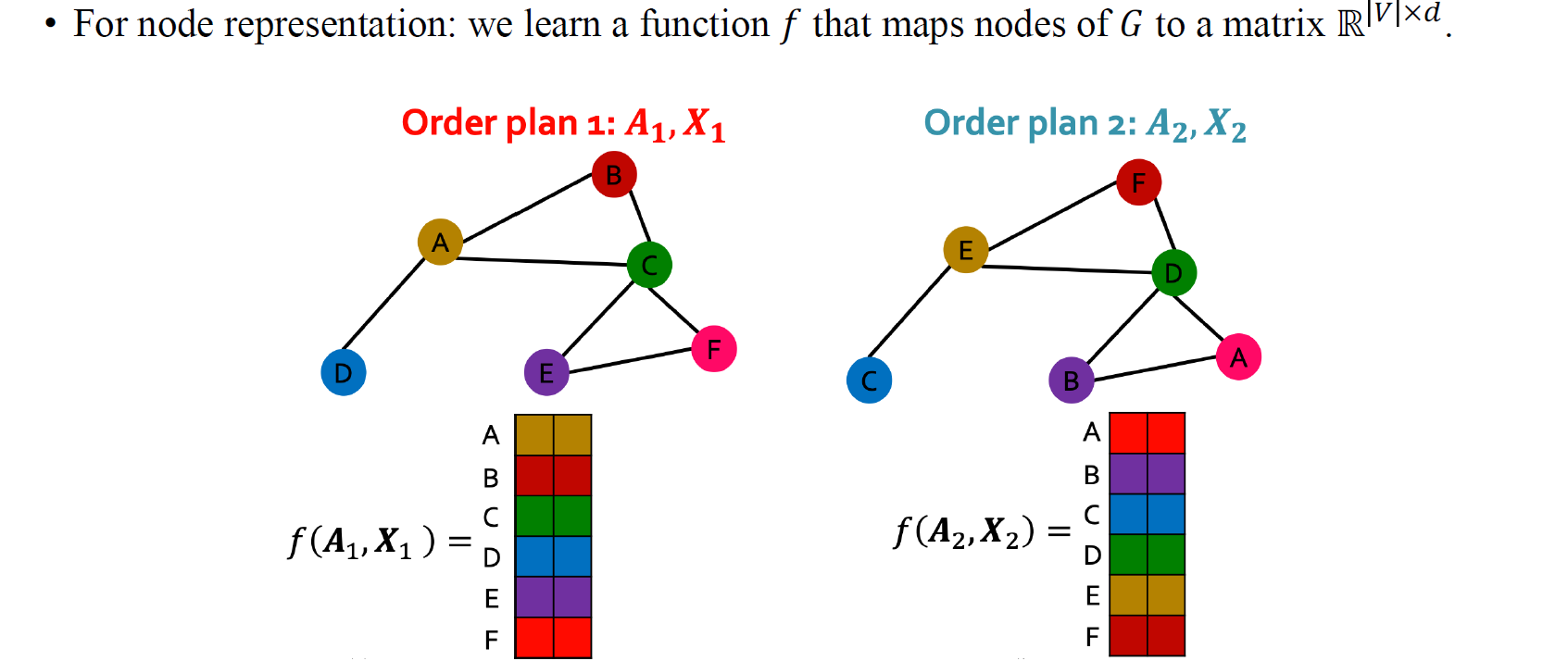때로는 또다른 확장된 개념이 필요할 것이고, 우리는 이를 permutation equivariance라고 한다. Permutation equivariance는 non classification problem에서 유용하게 사용될 것이다. 예를 들어, 어떤 $A$와 $X$로 구성된 graph가 주어지고 각 vertex의 label을 예측해야한다고 해보자. 만약 node의 순서가 변경되면 node label들이 집합인 output의 순서도 변경해야 할 것이다. 우리는 각 node의 label을 예측해야 하기 때문에 node들의 순서가 바뀌게 되면 이에 따라 예측한 label들도 순서가 바뀌어 대응되는 node들과의 관계를 유지해야 할 것이다.

이를 permutation invariance와 같이 수식으로 정의해보면, 만약에 특정 function $f$의 output인 $f(A,X)$에 permutation matrix $P$를 곱하게 되면, 이는 곧 $f(PAP^T, PX)$와 같아져야만 할 것이다.

Summary: Invariance and Equivariance

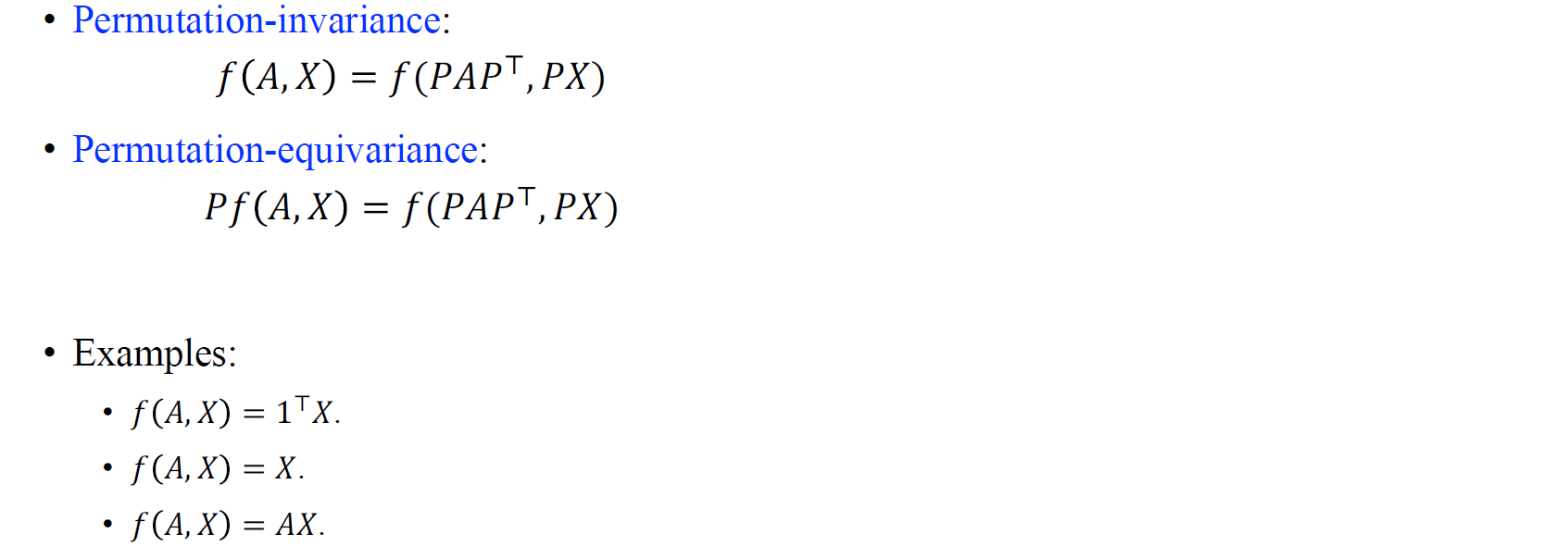요약하자면, permutation-invariance는 function output이 permutation에 따라 바뀌지 않는 반면에 permutation-equivariance는 function output이 permutation에 따라 바뀌게 된다. 그리고 여기서 permutation-equivariance는 function output에 permutation matrix로 정의한 순서에 따라 바뀌게 될 것이다. 우리는 이렇게 두가지 개념을 정의했기 때문에 이제는 graph convolutional network를 제대로 설명할 수 있게 되었다.