[그래프 기계학습] Graph Convolutional Network

GNN Overview

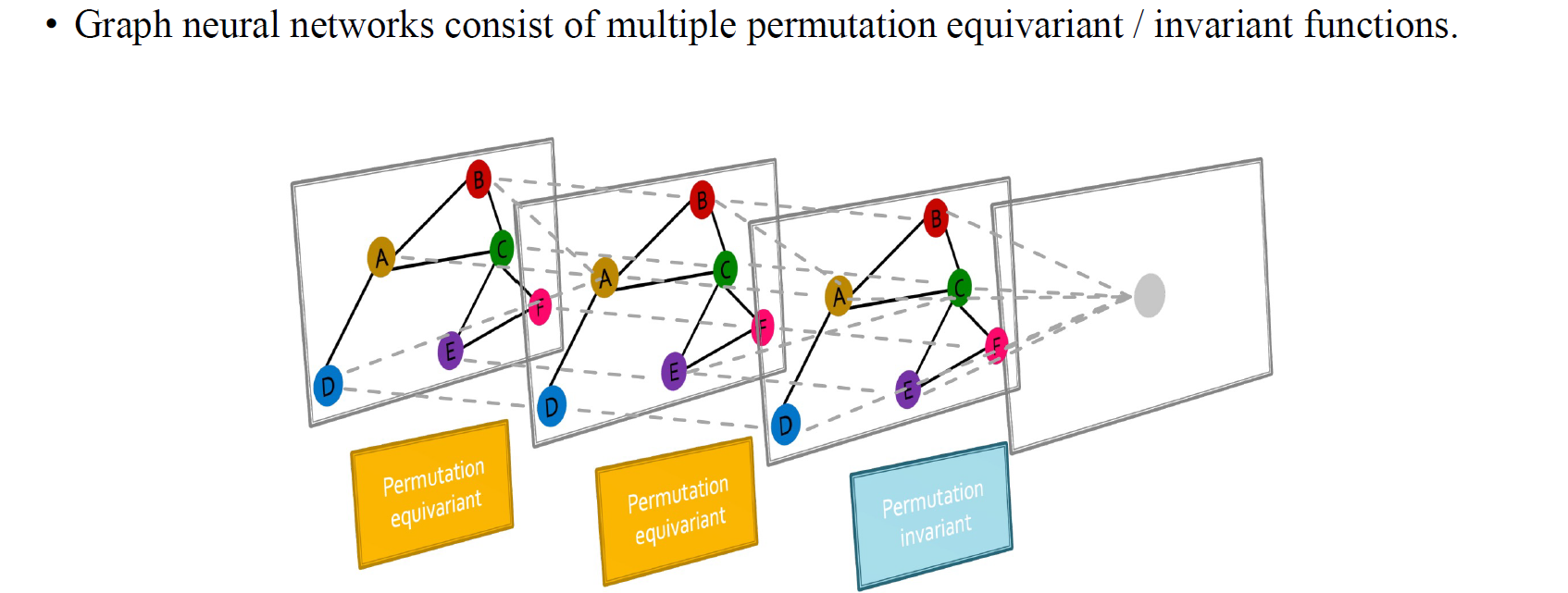Graph neural network(GNN)은 결국 여러개의 permutation equivariant/invariant function들로 구성할 수 있다. 이번에는 둘 중에서 permutation equivariant function에 초점을 두고자 한다.

Graph Convolutional Networks

Graph convolutional network (GCN)의 핵심은 node neighborhood에 기반한 convoltuion 연산이다. Node neighborhood node와 연결된 주변 node들을 지칭하며, 우리는 graph에서 각 edge에 따라 수행되는 propagation/transformation으로 GCN을 설명할 수 있다.

Overall Idea

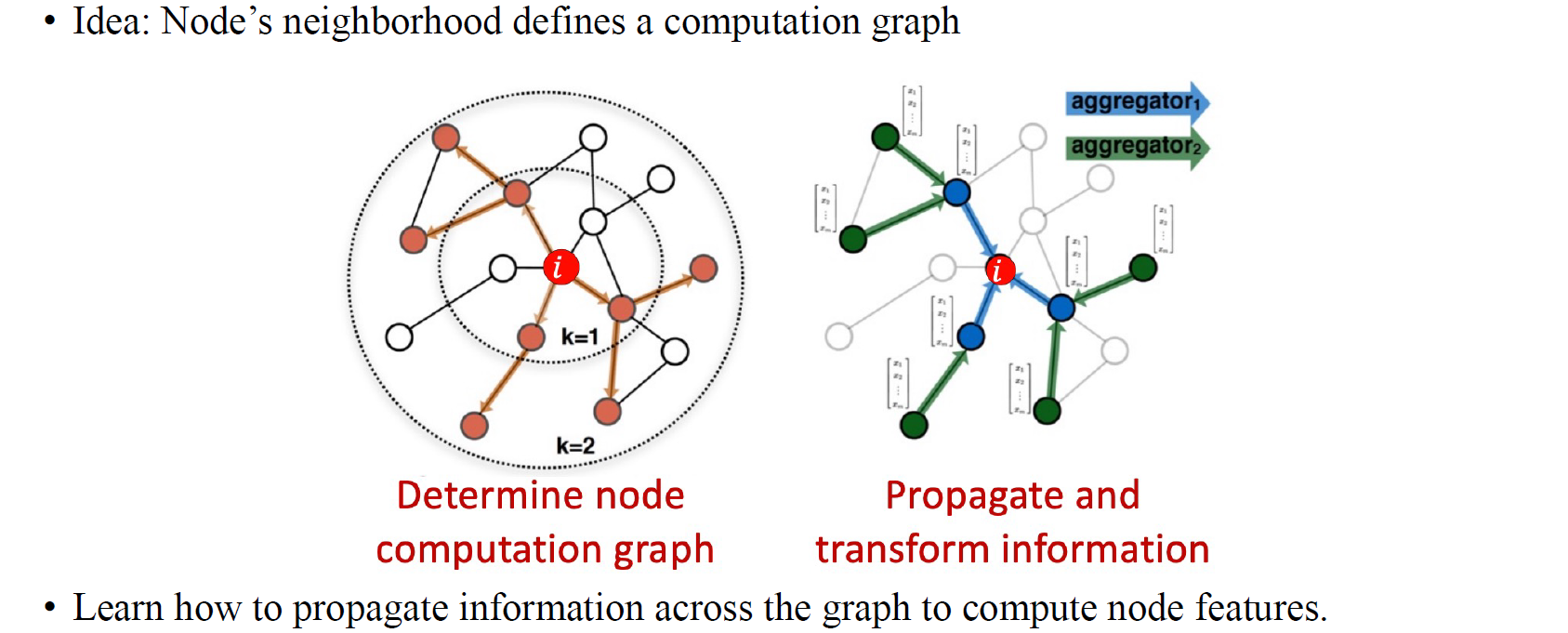
CNN의 경우 주변 pixel들의 정보를 모으는 aggregation 과정이 있다. GNN의 아이디어도 이러한 CNN의 방법과 상당히 유사하다. CNN의 embedding과 마찬가지로 GNN에서는 node마다 embedding을 만들기 위해서 주변 node들로부터 정보를 모으게 된다. 각 node마다 hidden feature를 update하기 위해서 local neighborhood들의 정보를 모으는 것이다.

바로 이웃한 node로부터 정보를 모으려면 layer를 한번만 쌓으면 된다. 하지만 더 멀리 있는 node들로부터 정보를 모으기 위해서는 그만큼 layer를 더 쌓아서 neural network를 깊게 설계하면 된다.

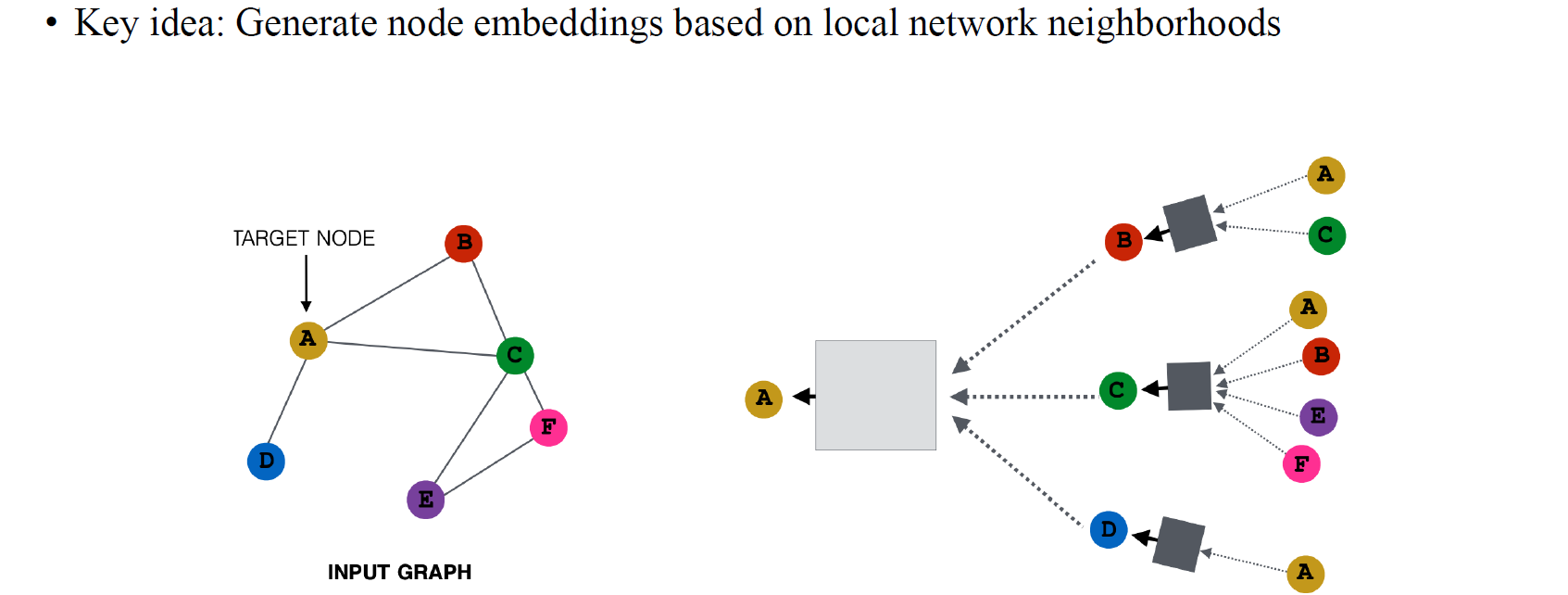
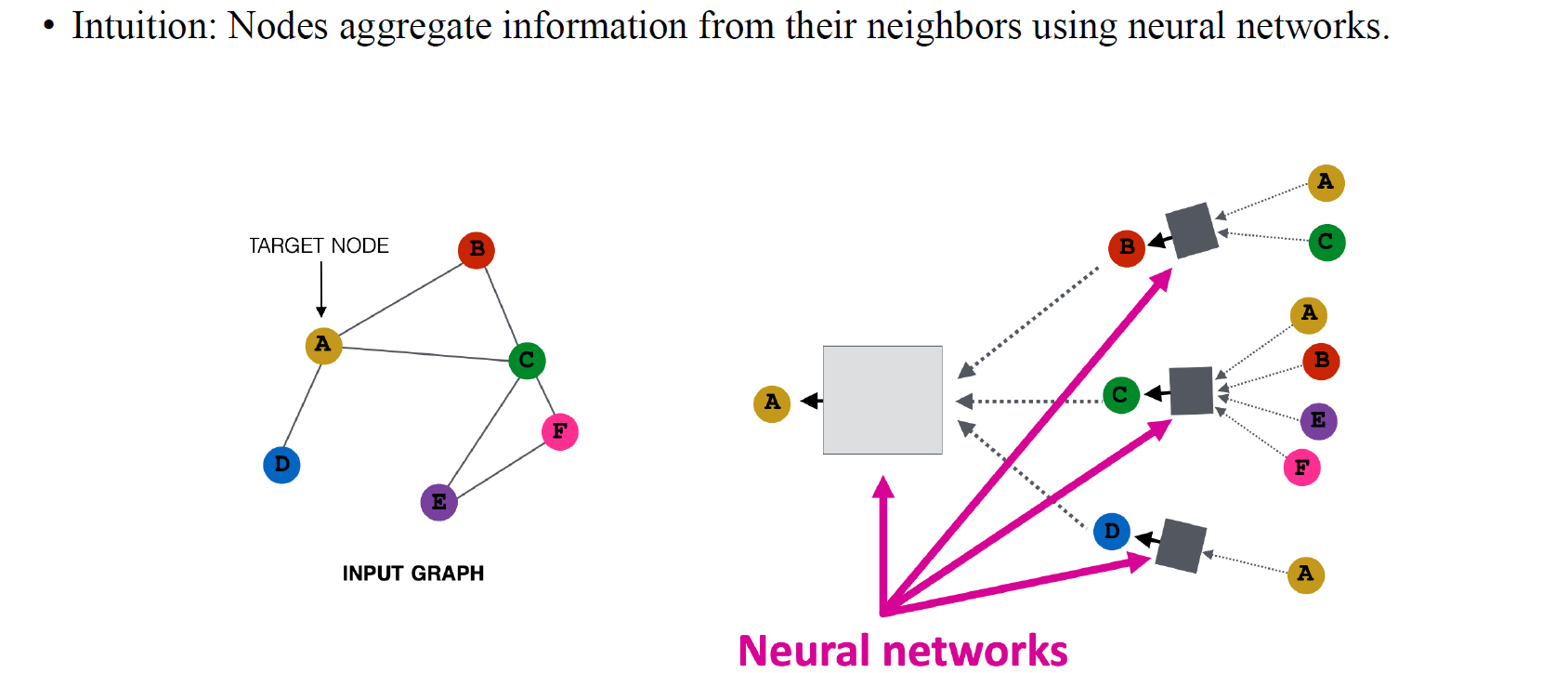
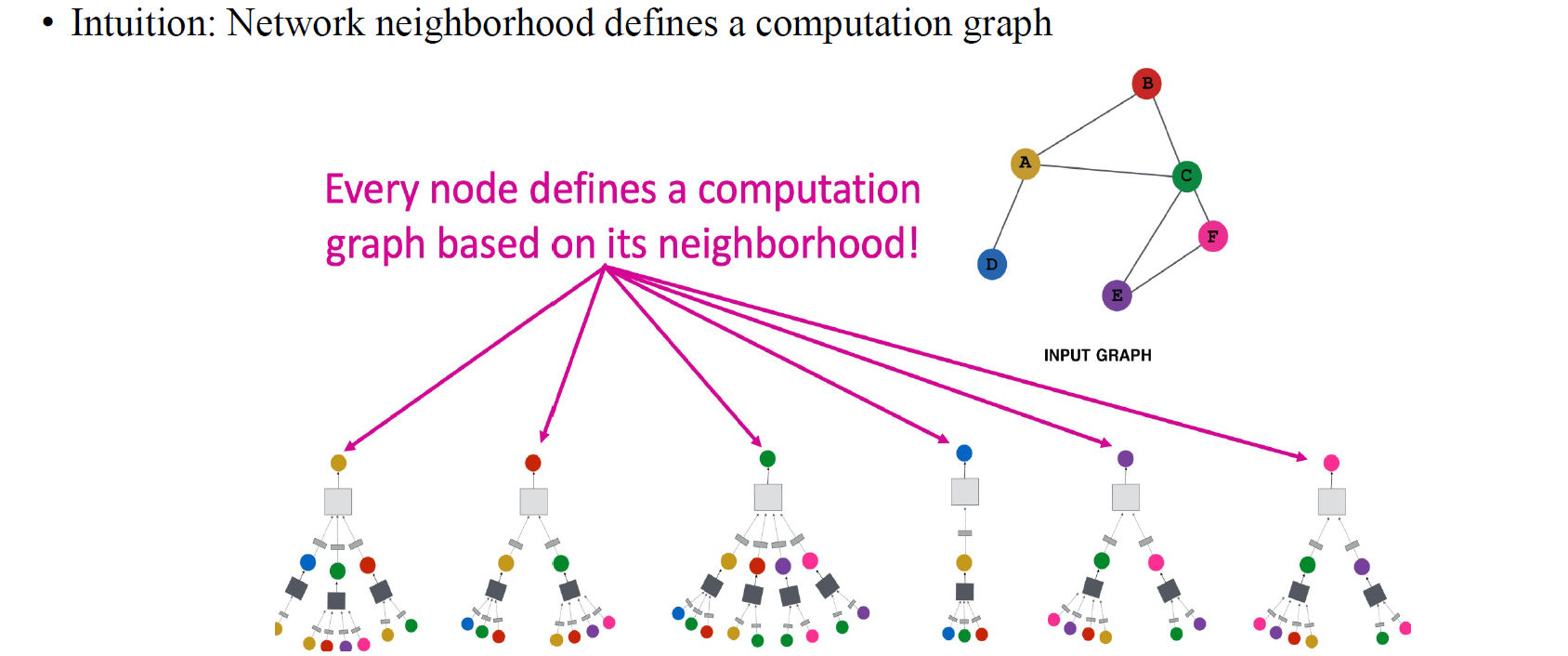이렇게 각 node마다 이웃한 node부터해서 멀리있는 node까지의 정보들을 모을 수가 있다. 이렇게 각 node마다 일종의 computation graph를 정의할 수 있게 된다. A를 기준으로하면 먼저 바로 이웃한 B,C,D의 정보를 가져오면, 이에 따라 B,C,D와 이웃한 node들의 정보까지 layer를 깊게 쌓으면 가져올 수 있게 된다. Aggregtation 과정은 linear layer와 activation function을 거치는 것과 동일한 맥락으로 이루어지게 된다. 결국 GCN의 전반적인 아이디어는 이러한 식으로 모든 node들이 본인들의 이웃들을 기반으로 새로운 computation graph를 정의하는 것에서 비롯되어 node마다 정보를 update하게 된다.

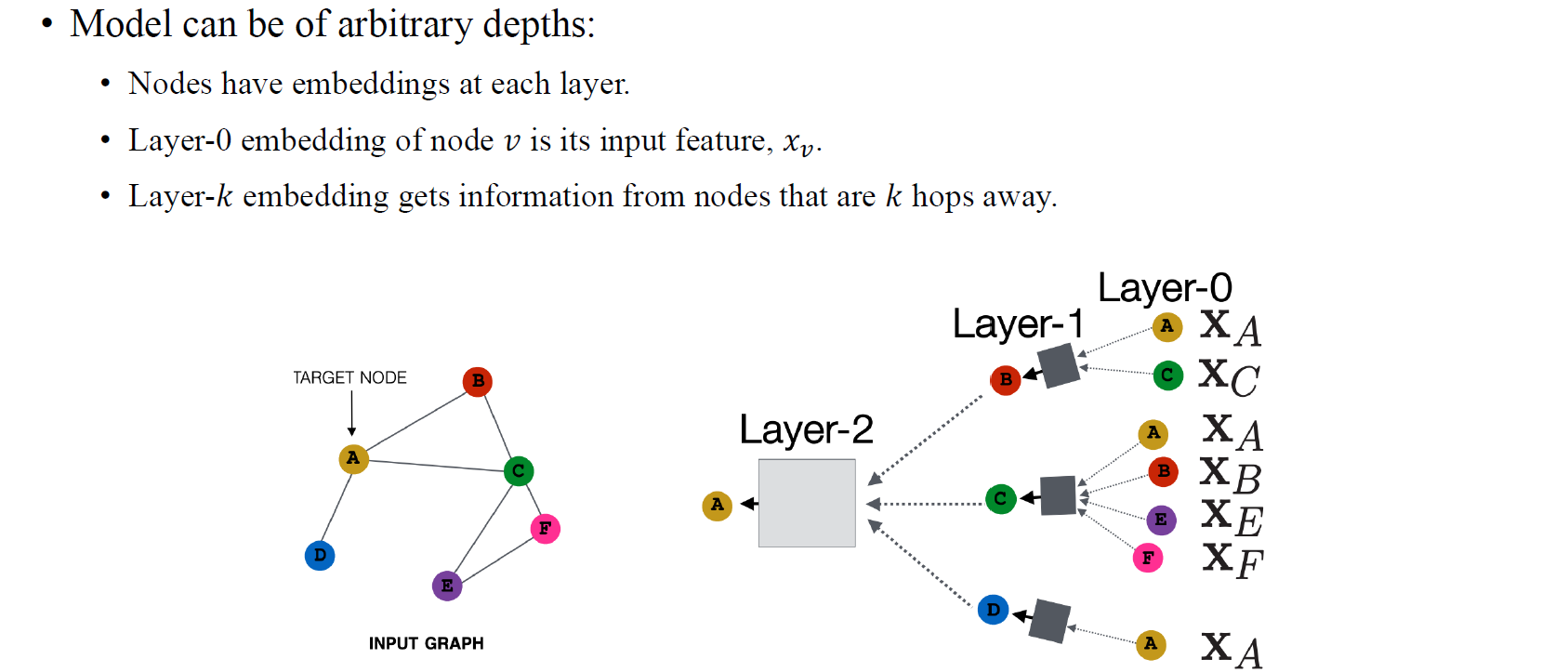GCN model은 임의의 depth를 가질 수가 있고, layer 0의 embedding은 일반적으로 input feature로 정의하게 된다. 그리고 최종 output을 결정하기 위해서 일반적으로 layer $k$의 embedding을 사용하게 된다.

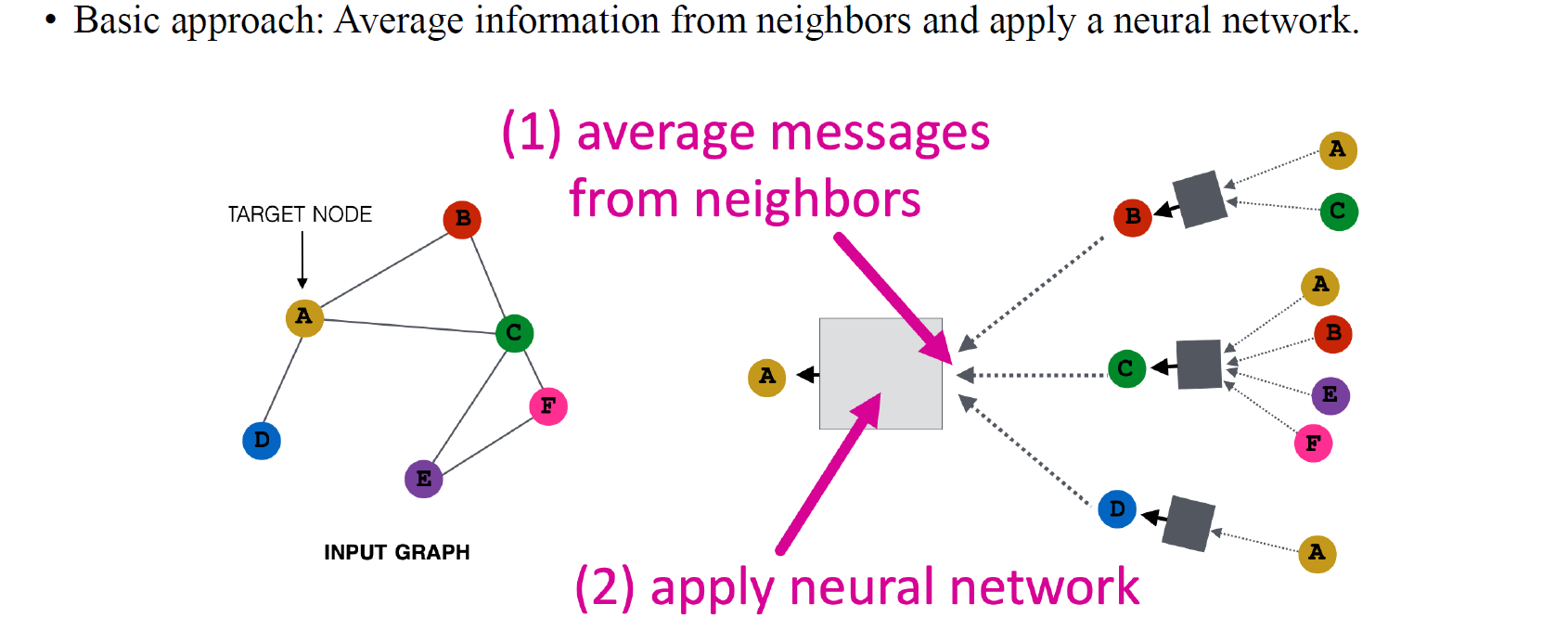기본적으로 GCN은 neighborhood로부터 정보를 aggregation하는 것과 neural network를 통해 모은 정보들로부터 본인을 update하는 것까지 해서 총 2-step으로 진행된다. 즉, 정보를 모아서 linear transformation과 non-linearity를 부여해서 output을 결정하면 되는 것이다.

GCN Implementation

우리가 실제로 GCN의 수식을 이해하게 된다면, neighbor message를 모으고 neural network를 적용하여 hidden embedding을 update하는 과정이 그리 어렵지는 않을 것이다. 일반적으로 GCN과 같은 GNN의 layer는 $k$ layer의 정보를 바탕으로 $k+1$ layer의 결과를 표현하게 된다.

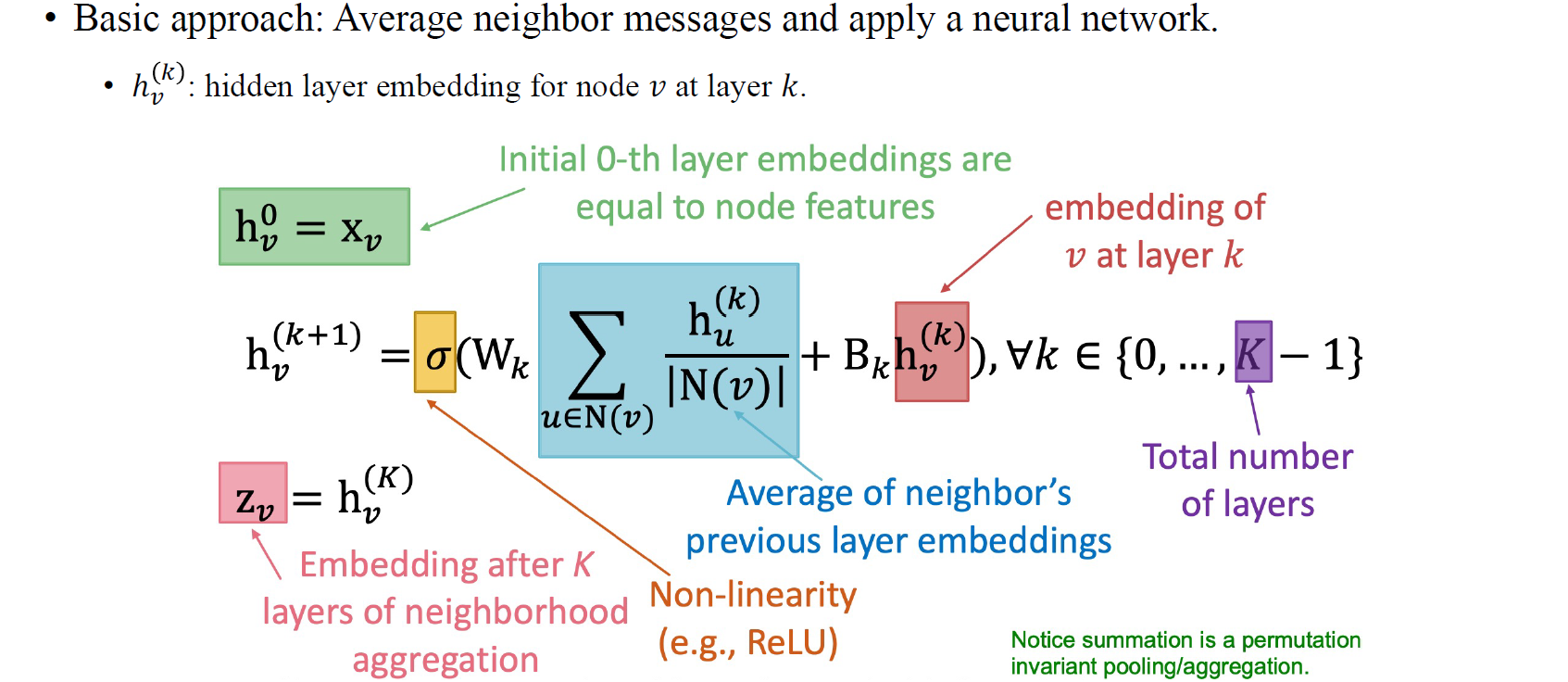GCN이 어떻게 돌아가는지 보기 위해서 node $v$의 feature $x_v$로부터 hidden feature $h_v^0$을 동일하게 정의해서 시작할 것이다. 각각의 node embedding을 $h_v^0$로 intialization하여 aggregation step을 neighborhood node $N(v)$의 embedding을 summation하여 average하는 과정으로 수행할 것이다. 특정 node $v$를 update하기 위해서 neighborhood node $u$들로부터 정보를 모으는 과정인 셈이다. 이웃 node의 개수로 나눠주는 과정에서 average 연산을 수행할 수 있다. 그리고 graph convolution을 보면 실제로 aggregation을 통해 얻어진 값들로 linear transformation이나 matrix multiplication을 수행하고, 추가로 activation function을 통해 non-linearity를 부여하게 된다. 이러한 과정을 우리는 update step으로 정의할 수 있고, neural network application step이 바로 이러한 과정들이다. Linear transformation과 더불어 이전 layer의 embedding과 관련해서 residual connection이 추가될 수 있지만, 상대적으로 중요한 부분은 아니다. 이렇게해서 얻어진 마지막 embedding $h_v^K$는 최종 output을 결정하기 위해 사용될 것이다.

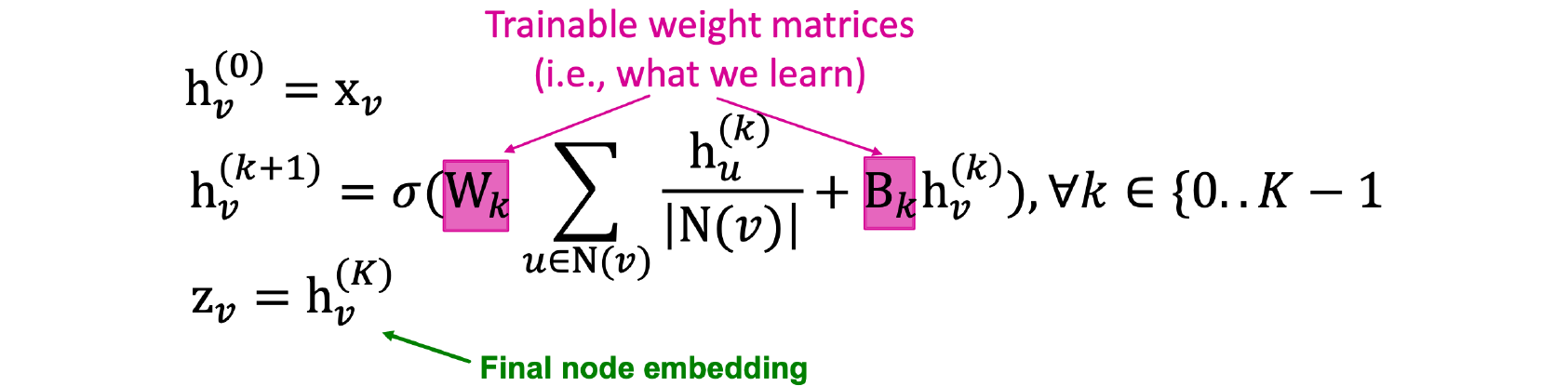여기서 $W_k$와 $B_k$는 학습 가능한 weight matrix들이다. 여기서 흥미로운 부분은 weight matrix가 vertex와 independent하다는 점이다. $W_k$의 차원은 오로지 node embedding의 차원과 관련이 있고, 전체 graph의 크기와는 관련이 없다. 이러한 부분이 graph의 크기가 바뀌는 문제를 처리할 수 있게 한다.

GCN: Invariance and Equivariance

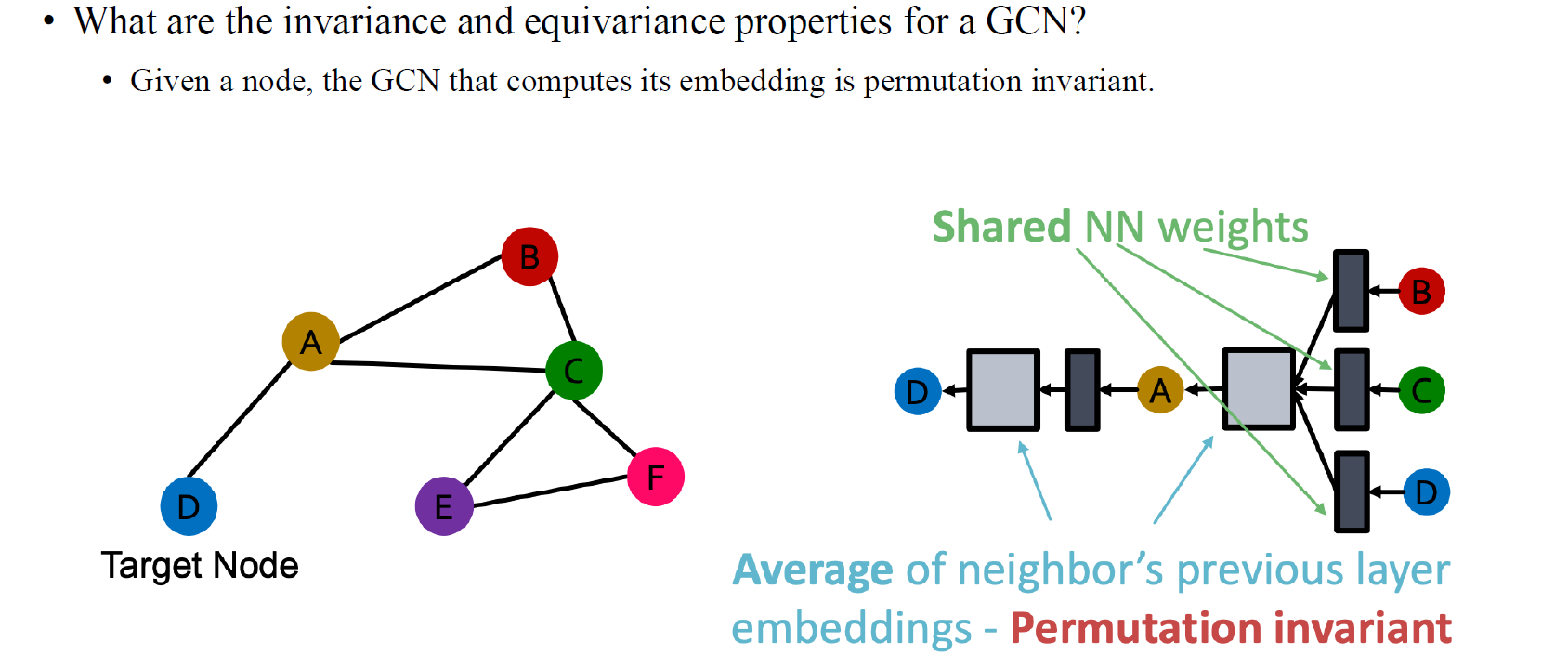또한, 우리는 꽤 쉽게 invariance / equivariance 성질을 지니는 GCN을 얻을 수가 있다.

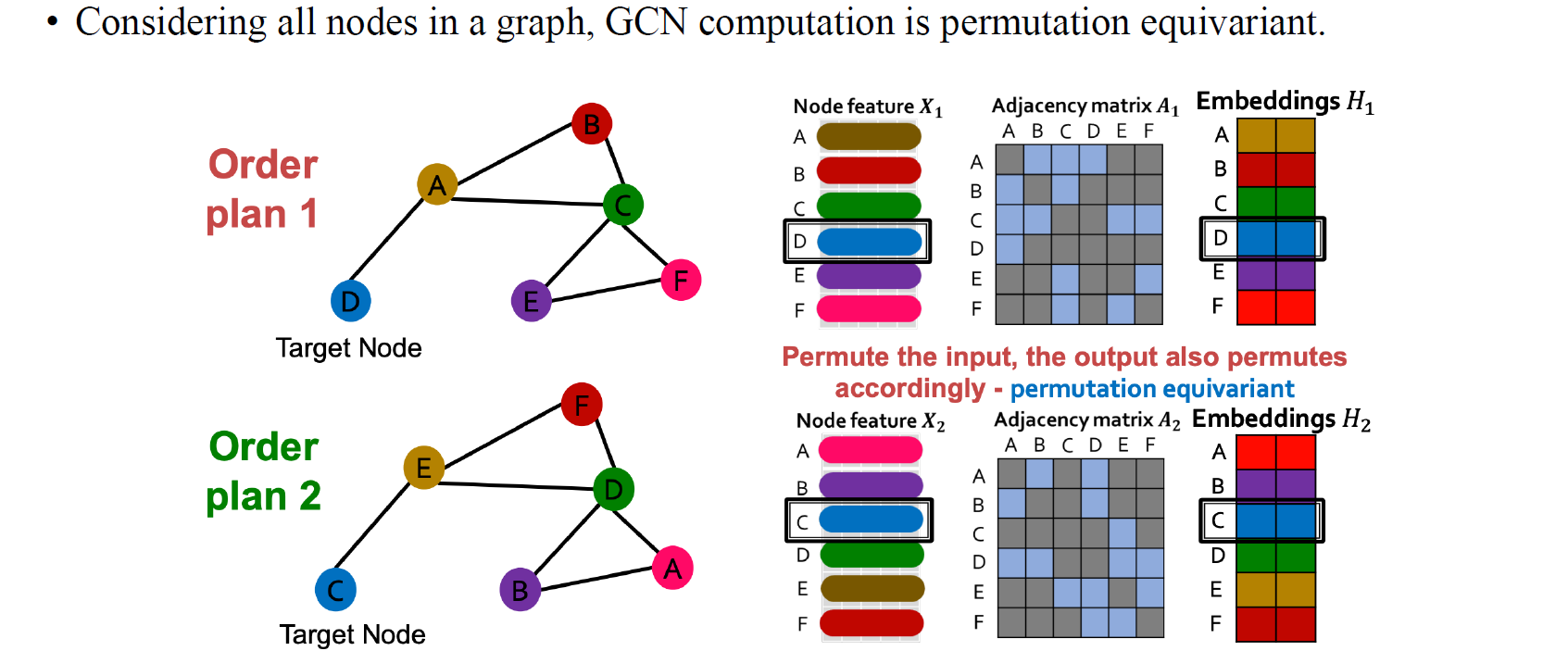위와 같이 order plan이 2가지가 있다고 해보자. Aggregation step을 잘 생각해보면 우선 첫번째 예시에서 target node D와 B,C가 A와 연결되어 있는걸 볼 수 있고, 이들은 어떠한 order plan과 상관없는걸 알 수 있다. 순서를 어떻게 바꾸든 상관없이 aggregation step에서는 이웃한 node들만 참고하기 때문에 순서는 상관없다는걸 알 수 있다. 즉, 이웃한 node들은 aggregation step에서 ordering이 바뀌더라도 영향을 받지 않을 것이다. 그래서 GCN의 aggregation step에서 이웃한 vertex들은 permutation이 있음에도 불구하고 순서가 바뀌지 않게 되는 것이 핵심이다. 그리고 aggregation이 일종의 summation이나 average와 같아서 이러한 aggregation operation은 vertex의 ordering과는 독립적인 연산이 되는 것이다. 이러한 식으로 aggregation step은 permutation과 관련이 없는 permutation-invariance를 만족하게 된다.

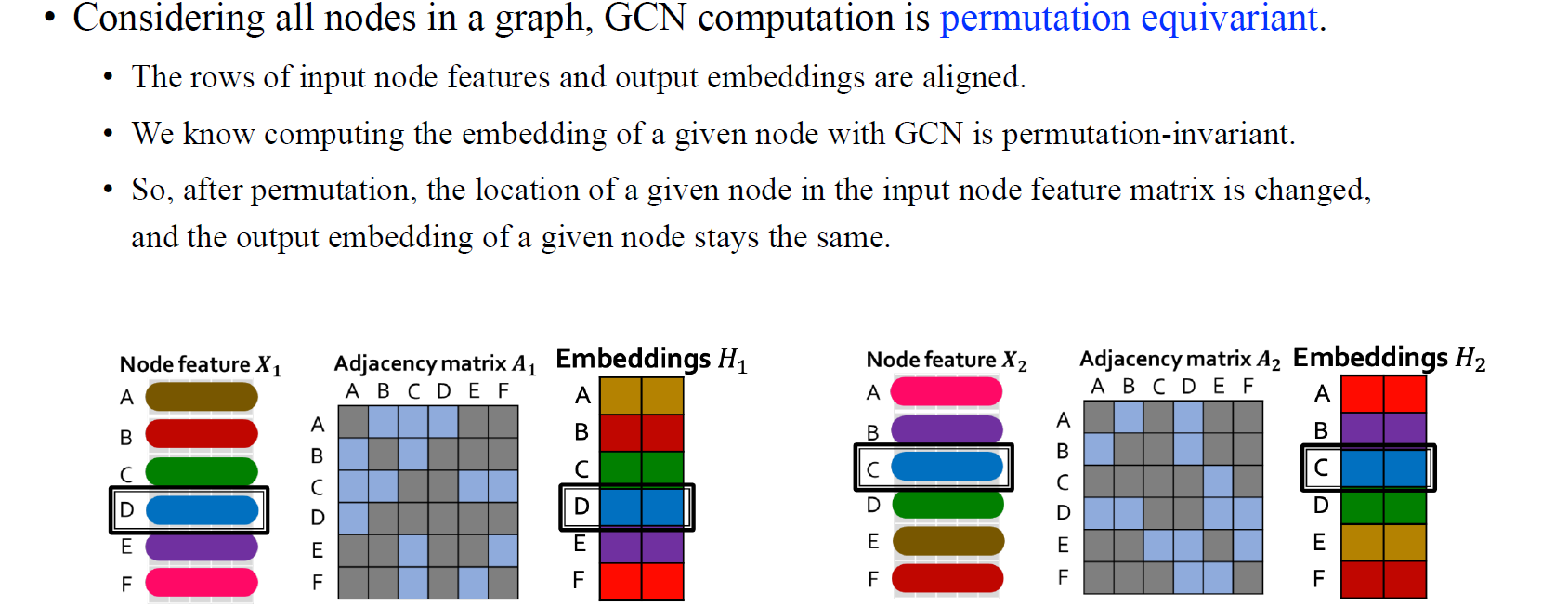하지만 output의 경우 각 vertex들과 관련이 있기 때문에 node embedding이 permutation equivariant한 성질을 지니게 된다. 그래서 output이 input permutation의 영향을 받아 바뀌게 될 것이다.

Matrix Formulation of GCN

GCN을 이해하는데 필요한 또 다른 핵심은 전반적으로 복잡한 message passing step이 일종의 matrix multiplication으로 간주될 수 있다는 점이다. 특히, 우리는 GCN을 adjacency matrix, node feature matrix, weight matrix 사이의 matrix multiplication으로 생각할 수 있고, 이를 통해서 GNN의 output을 만들 수가 있다. 즉, 간단하게 $AXW$로 GCN을 수행할 수 있다는 것이다. 이는 GCN에 있어 매우 중요한 사실이다.

그리고 GCN은 또한 sparse matrix multiplication으로 표현될 수 있다. Adjacency matrix $A$는 보통 값이 0인 부분이 많은 sparse matrix일 것이다. 아무래도 전체 graph가 fully connected가 되어있는 상황보다는 edge로 특정 vertex가 연결된 상황들이 대부분일 것이기 때문이다. 그렇기 때문에 $AXW$를 계산할 때 사용되는 $A$가 sparse matrix라서 computation complexity가 굉장히 작아질 것이다.

그래서 대부분의 aggregation에서 sparse matrix에 의해서 효율적으로 계산이 될 것이고, GCN update의 식을 결국에는 matrix multiplication으로 대체할 수 있다는 것이 실제 GCN 연산의 핵심이다. 여기서 $k$번째 layer에서 $v$번째 node에 대한 hidden embedding $h_v^k$가 있을 때, 모든 vertex $v$에 대해서 concat하여 hidden embbeding matrix $H^k$를 구성해서 output을 구할 수가 있게 된다.

다시 $H^k$를 $k$번째 layer에서의 hidden node embedding을 concat한 matrix라고 해보자. 그러면 $v$번째 vertex의 이웃들로부터의 정보의 합인 $h_u^k$의 summation 결과가 adjacency matrix에서의 $v$번째 row와 hidden embedding matrix의 vector multiplication과 같아지게 된다. 그리고 이를 모든 vertex들에 대해서 구한 결과를 concat하게 되면 결과적으로 matrix간 multiplication과 같아지게 될 것이다.

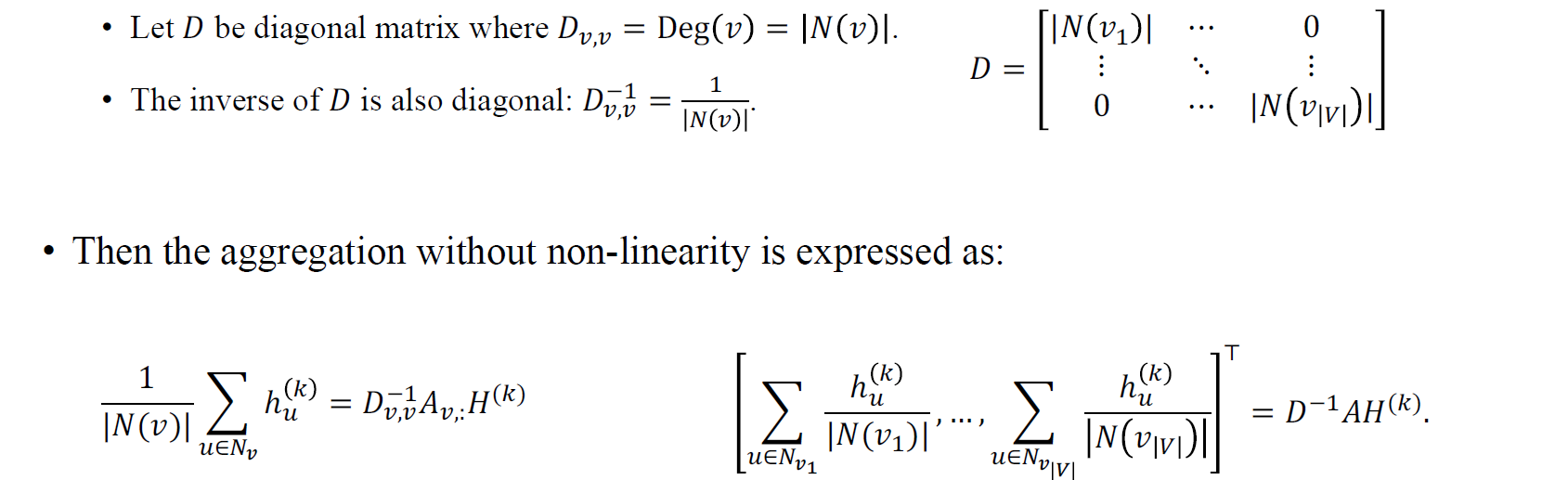여기에 추가적으로 degree 정보로 $h$를 나눠주어 aggregation을 average 형태로 만들 수가 있고, 이는 $AX$에 degree matrix $D$의 inverse를 곱해준 결과와 같아지게 된다. 이는 결국 normalization과 같은 맥락이고 지금까지의 과정이 weight를 곱해주기 전에 이웃들로부터 정보를 모으는 과정까지 진행한 결과이다.

마지막으로 각각의 node embedding에 weight matrix를 곱해줘야 한다. $k$번째 layer에서 동일한 weight matrix를 각각의 node embedding에 곱해주게 되고, 여기서 weight matrix의 크기는 vertex의 개수와 상관없이 feature의 차원으로 구성되기 때문에 hidden node embedding 우측에 곱해주게 되는 것이다.

정리해보면 $H^k$는 vertex의 수와 node feature의 차원으로 구성된 matrix이고, 이 matrix의 row는 하나의 vertex에 대한 정보를 담고 있으며 이를 모두 concat한 결과인 것이다. 특정 위치의 vertex의 connectivity 정보는 adjacency matrix에서의 특정 위치의 row가 가지고 있기 때문에 이를 이용해서 원하는 vertex를 고를 수 있고, 이를 모든 vertex에 대해서 수행해야하기 때문에 adjacency matrix는 vertex의 차원으로 형성된 squared matrix로 좌측에 곱해지게 되는 것이다. 그리고 우리는 모든 vertex에서 균일하게 weight를 적용시키기 위해서 vertex의 차원과 무관하게 feature 차원으로 구성된 weight matrix를 우측에 곱하게 되는 것이다.

이렇게 GCN을 matrix multiplication으로 동작할 수 있으며, $AXW$에서 좌측은 aggregation step이고 우측은 update step을 담당하게 된다. 여기에 이제 non-linearity를 주기 위해서 ReLU와 같은 activation function을 마지막에 취해주면 되는 것이다. 지금까지 살펴본 내용들로부터 결국 sparse matrix multiplication에 의해 GCN을 효율적으로 사용할 수 있음을 말하고 있는 것이다.

한가지 의문점으로 sparse matrix multiplication인데 $HW$가 sparse하지 않다고 주장할 수 있다. 하지만 $AH$가 sparse하며 $W$의 크기가 앞선 matrix들보다 상대적으로 많이 작을 수 있기 때문에 우리는 이 결과를 sparse matrix multiplication으로 볼 수 있는 것이다. Social network를 보면 adjacency matrix가 굉장히 크면서 sparse할 것이다.

Supervised Training

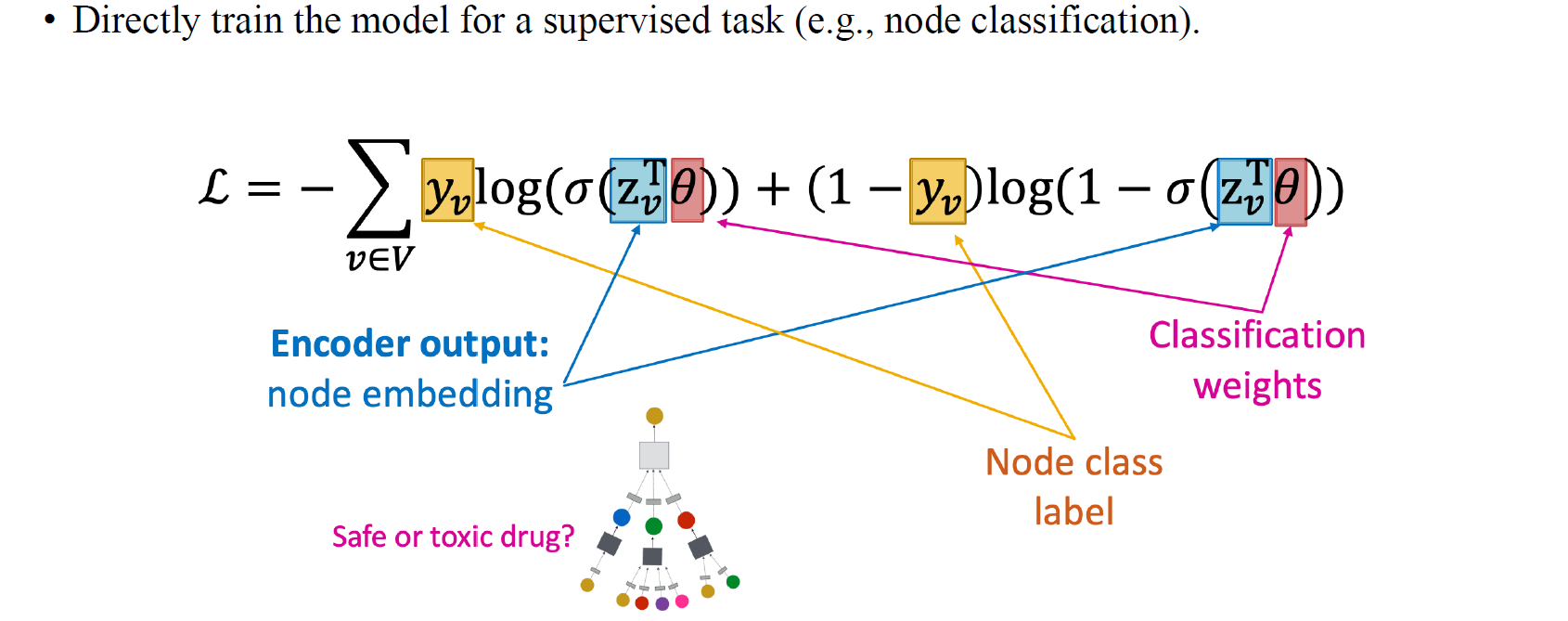GCN이 어떻게 돌아갔는지 알아봤으며, 이를 통해 나온 embedding output과 실제 label을 이용하여 supervised training을 위와 같은 loss function을 구성해서 수행할 수 있을 것이다.

Model Design: Overview

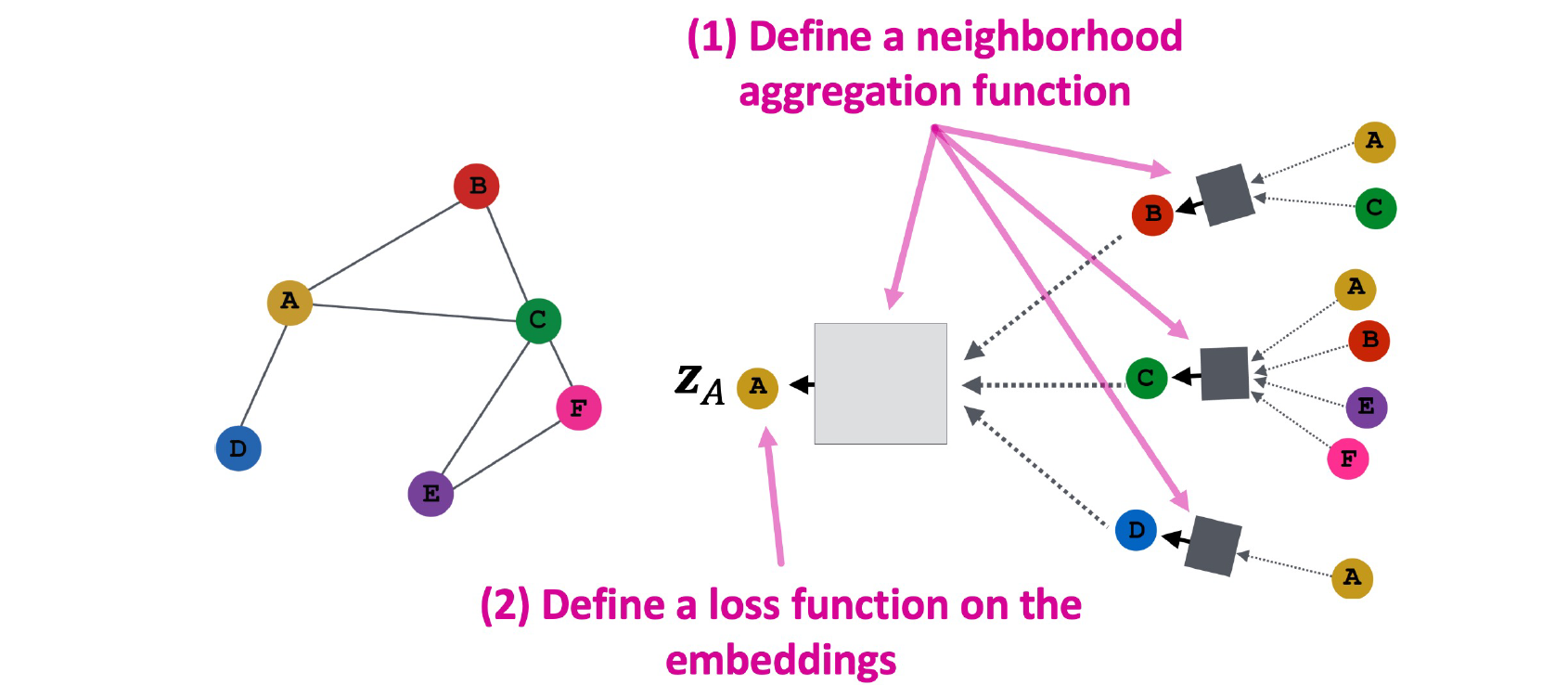우리는 neighborhood aggregation function과 embedding으로부터 loss function을 정의함에 따라 GCN을 정의할 수 있다. 이후에 어떠한 task에 어떠한 loss function을 세워야하는지와 관련해서 구체적인 내용을 설명할 것이다. 지금은 그보다 neighborhood aggregation function을 정의하는 부분에 더 초점을 맞추는 것이 중요하다.

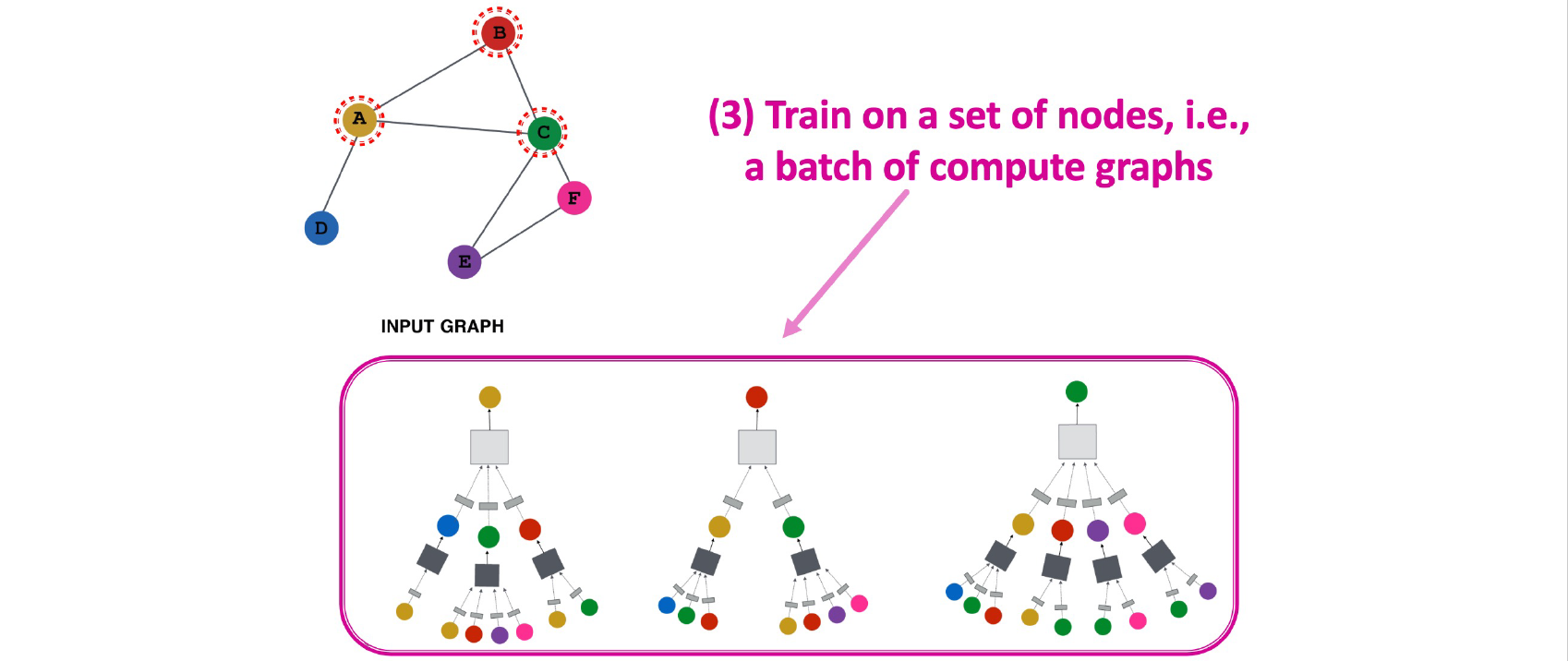이제 각 vertex마다 일종의 computational graph를 이웃한 vertex들로 구성해서 aggregation과 update를 통해서 GCN을 학습시킬 수 있다.

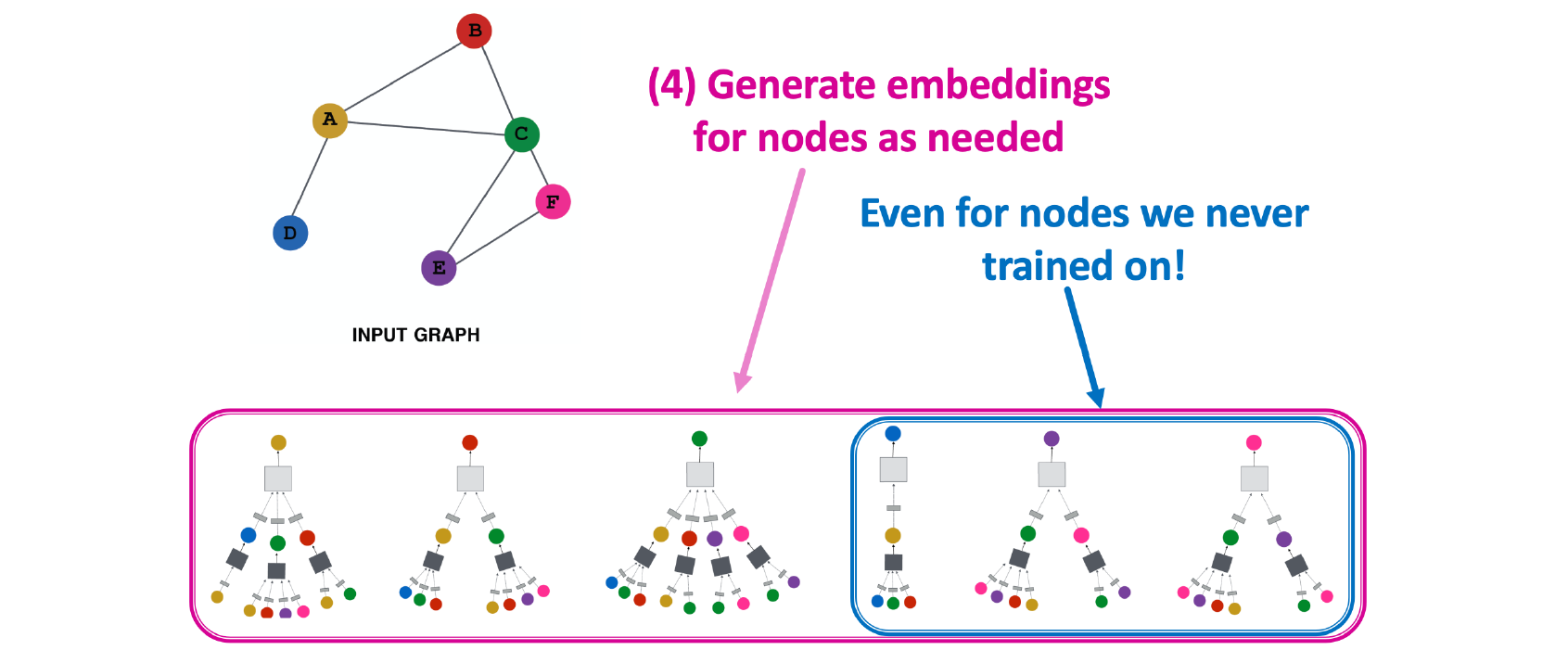여기서 각 vertex마다 구성할 수 있는 computational graph가 사실은 graph의 구조에 의존적이지 않기 때문에 우리가 train에서 보지 못한 vertex가 있더라도 학습한 GCN을 적용시킬 수가 있다는 것이 GCN의 성질 중 하나이다.

Inductive Capability

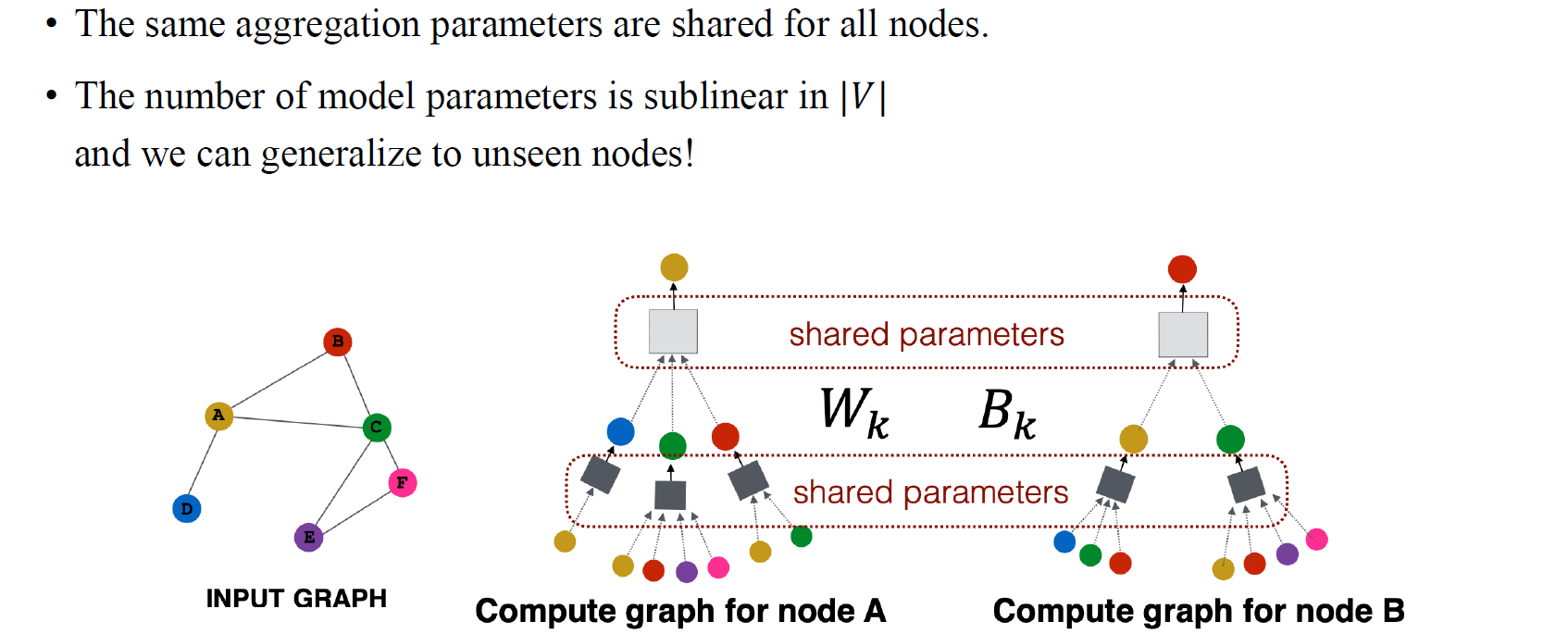이렇듯 GCN의 흥미로운 부분 중 하나가 동일하게 학습된 parameter들이 모든 vertex에 공유될 수 있다는 점이다. 이것이 의미하는 바는 parameter의 수가 고정되어 있어서 우리가 보지 않은 vertex들에 대해서도 동일한 parameter를 그대로 적용할 수가 있다. 이러한 맥락은 결국 기존의 CNN과 유사하다고 볼 수 있다. CNN은 kernel parameter를 학습하기 때문에 이것이 모든 pixel에 공유되는 것과 같은 맥락으로 볼 수 있다.

Inductive Capability: New Graphs

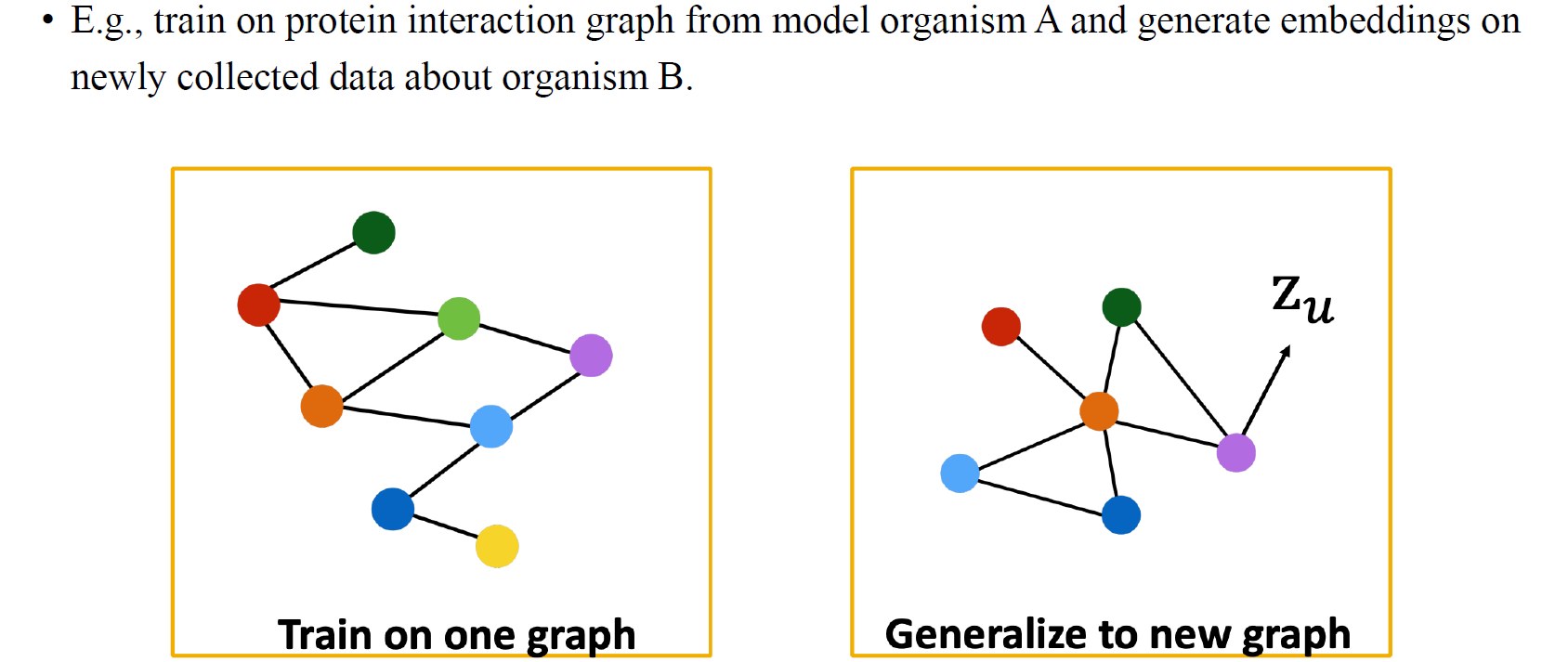물론 우리는 graph의 구조가 다르더라도 GCN을 새로운 graph에 generalization할 수 있어야 한다. Graph의 구조가 조금씩 달라짐에 따라 이로부터 node embedding을 update해야하는데, 여기에도 여전히 GCN을 적용할 수가 있다는 것이다.

Inductive Capability: New Nodes

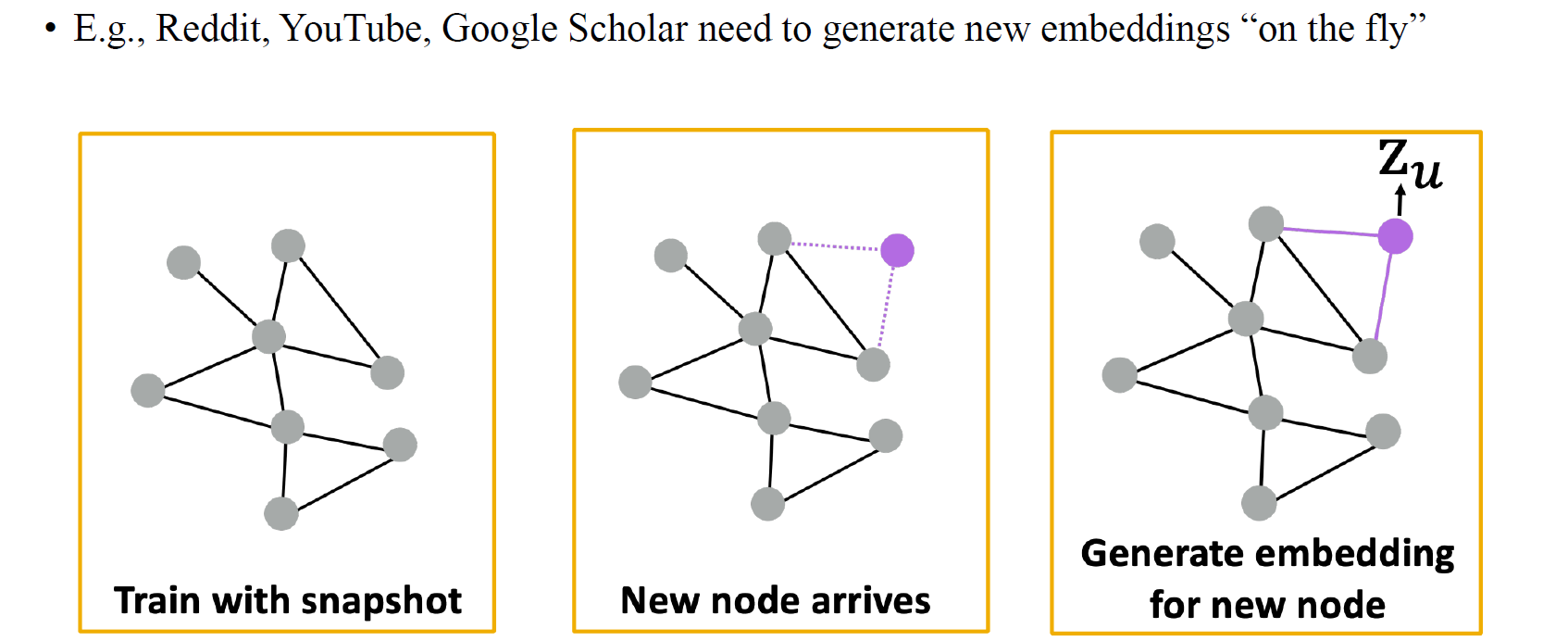아니면 기존의 graph에서 만약 node가 새롭게 추가되어 들어오더라도 우리는 GCN을 적용해서 새로 들어온 node로부터 node embedding을 얻을 수가 있다. 결국 node의 개수와 무관하게 parameter를 update할 수 있기 때문에 이러한 식으로 유연하게 GCN을 적용시킬 수가 있을 것이다.

A GNN Layer from General Perspective

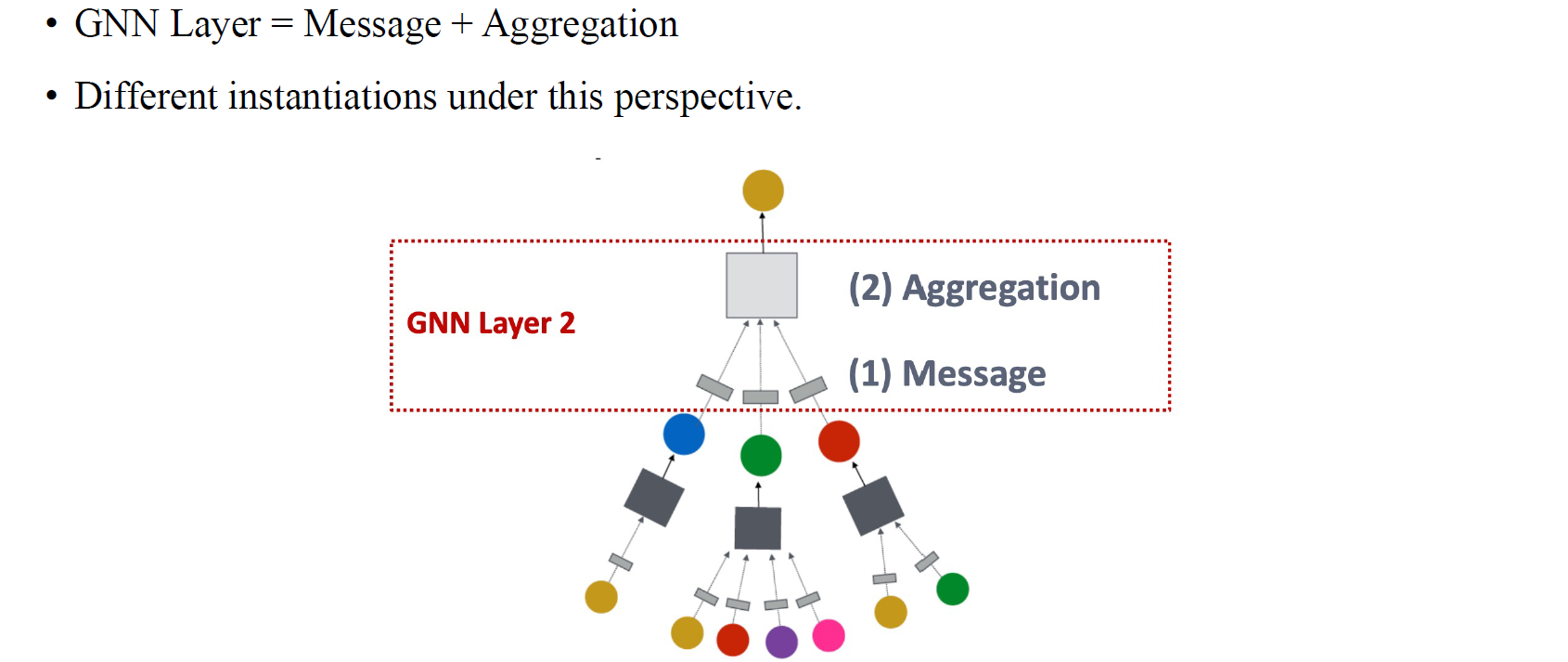GCN은 GNN의 초기 모델 중 하나로, GNN layer의 경우 좀 더 일반적인 관점으로 표현될 수가 있다. 그래서 일반적으로 GNN layer는 message passing과 aggregation으로 구성되어 있고, GCN은 convolution 연산을 통해서 2가지 과정을 수행하는 모델인 셈이다. 대부분의 GNN 모델들을 살펴보아도 이렇게 2개의 단계로 구성되어 있을 것이고, GCN은 2017년도에 등장했던 새로운 GNN 모델 중 하나인 것이다. 이후에도 다양한 변형 모델들이 등장하였으며, 여러 모델들이 등장한 이후에 사람들이 GNN layer는 결국 message passing과 aggregation로 설명할 수 있겠다고 정의한 것 뿐이다.

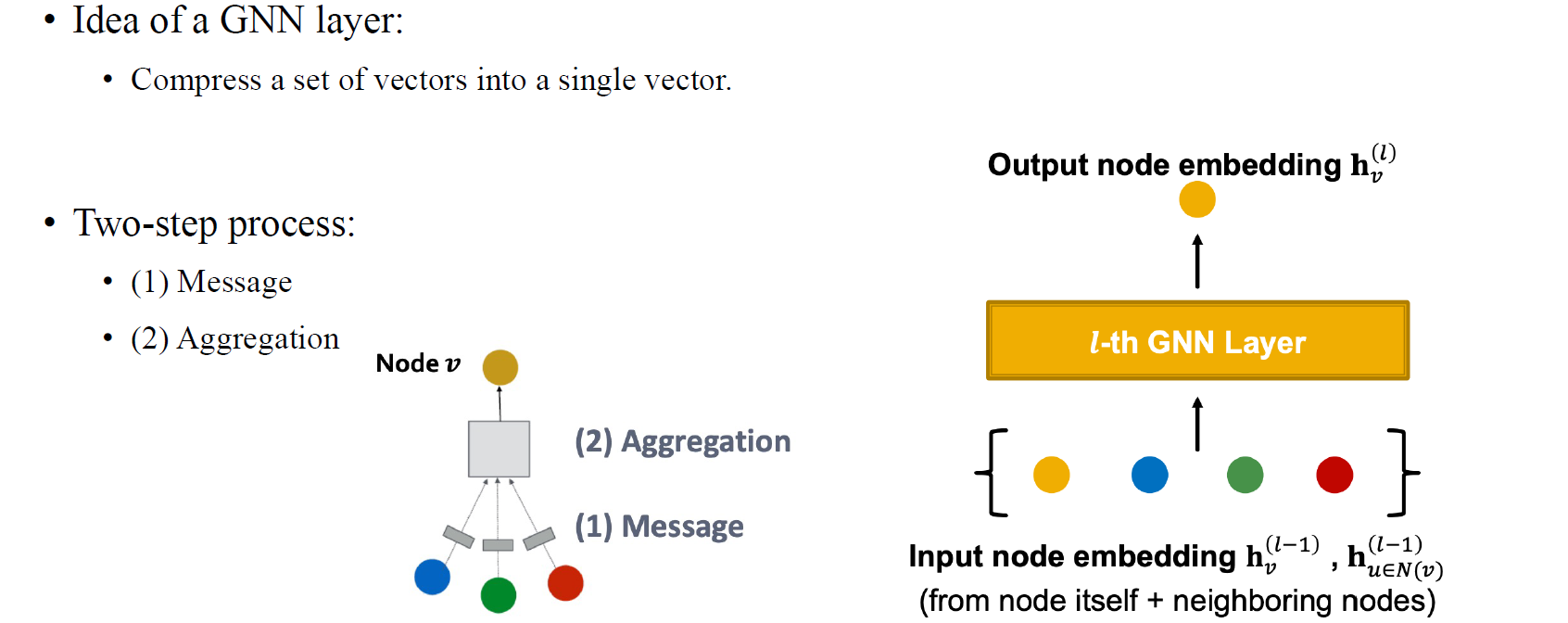GNN layer의 아이디어는 결국 여러 vector들을 하나의 vector로 압축시키는 과정이고, 이 과정은 결국 message computation을 먼저 하고 이들을 다시 aggregation하는 과저을 통해서 수행하게 된다.

Message Computation

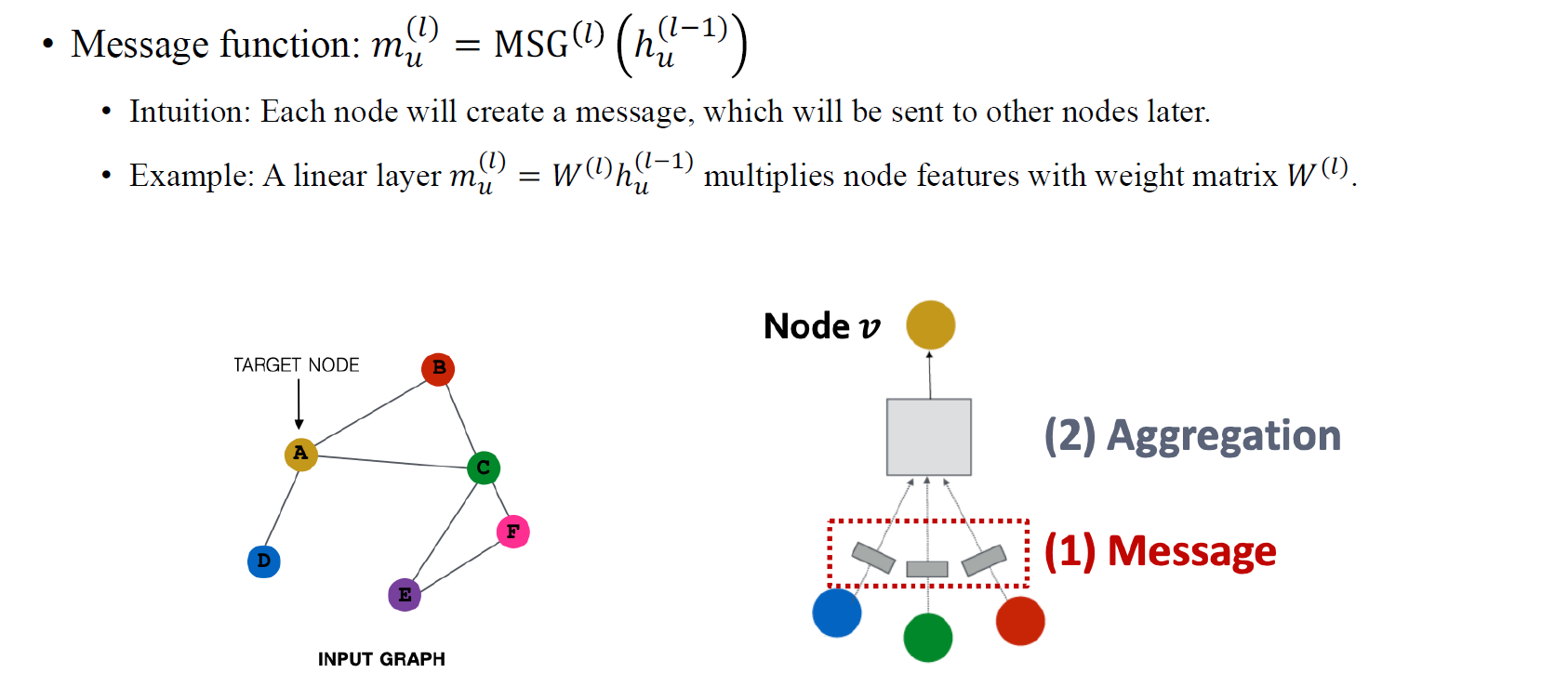먼저 message function MSG가 하는 것은 일반적으로 linear transformation과 같다. 어떤 vertex $h_u$가 주어지고 $l-1$ layer에서 node embedding이 주어졌을 때, weight matrix를 곱해줌으로써 이 feature를 처리하여 전달하고자 하는 message로 만들고 싶은 것이다. 이 과정이 message computation step이 해야하는 일이다. 이렇게 모든 node들이 message를 형성하게 되면 이들을 이웃 vertex들로 전달해야 한다. Message를 전달하기 위해서 matrix multiplication 등의 연산으로 message를 만들어야 한다.

Message Aggregation

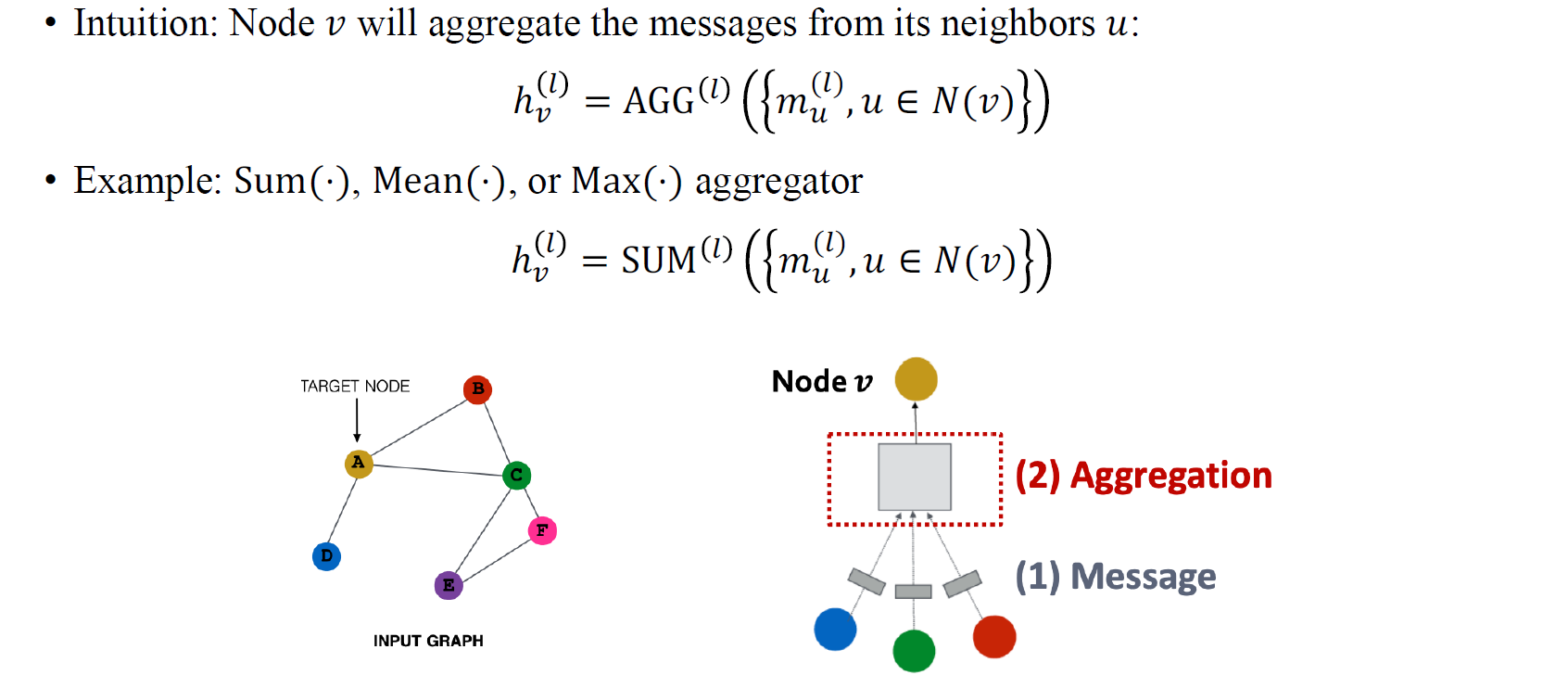다음으로 이웃 vertexe들에서 만들어진 message들을 가지고 aggregation 과정을 수행해야 한다. Aggregation function AGG는 message value들에 적용해서 하나로 정보를 모아주게 된다. 이웃 vertex $u$로부터 만들어진 message $m_u$들을 모으는 과정에서 대표적으로 Sum, Mean, Max aggregation 등을 수행할 수 있다. 이때 주의해야하는 부분은 message value들이 결국 고정된 크기의 값들이 아니면서 어떠한 순서를 가질 필요가 없기 때문에 sum, mean, max와 같은 개수와 순서에 independent한 연산들을 사용해야 한다.

Message Aggregation: Issue

만약 node $v$가 message aggregation을 한다고 하면 $v$의 이웃들의 정보만 사용하게 될 것이다. 그렇게 되면 원래 node $v$가 가지고 있던 정보는 사용하지 않았기 때문에 잃어버리게 될 것이다. 특히 우리가 node의 label을 예측해야하는 node classification을 한다고 하면 각각의 node가 지닌 정보들이 굉장히 중요할 것이다. 비록 이웃한 node들이 본인 node와 관련있는 정보들을 담고 있다고 하더라도 본인의 정보를 사용하지 않으면 정확하게 해당 node를 분류할 수 없게 된다.

그래서 이러한 문제를 해결하기 위해서 기존의 이웃 node들의 정보를 aggregation하는 과정에 추가로 본인의 message를 보존할 수 있는 방법을 추가해주고자 한다. 기존의 message aggregation 결과에 본인의 이전 hidden feature를 concat하거나 더하는 식의 방법이 있을 수 있다. 또한 근본적으로 자신을 연결시켜주는 self-loop를 처음부터 존재한다고 가정하면 message computation과 aggregation에 반영될 수 있을 것이다.

A Single GNN Layer

정리해보면 GNN layer 하나는 message compuation과 aggregation의 총 2가지 요소로 구성되어 있다. Message step에서는 feature를 처리해서 이웃에게 보낼 message로 만들어주고, aggregation step에서는 전달 받은 message들을 모아주게 된다. 결국 우리는 message와 aggregation을 이어 붙여서 여러 layer의 GNN을 구성하게 될텐데, 여기에 expressive power를 높여주기 위해서 non-linearity를 추가할 수가 있다. 여기서 중요한건 message나 aggregation step 모두 일종의 function이기 때문에 그 순서는 크게 중요하지 않고, 그렇기 때문에 non-linearity를 추가하기 위해서 activation function을 추가한다고 했을 때 어디에 하든지 크게 중요한 부분은 아닐 것이다.

Graph Convolutional Network (GCN)

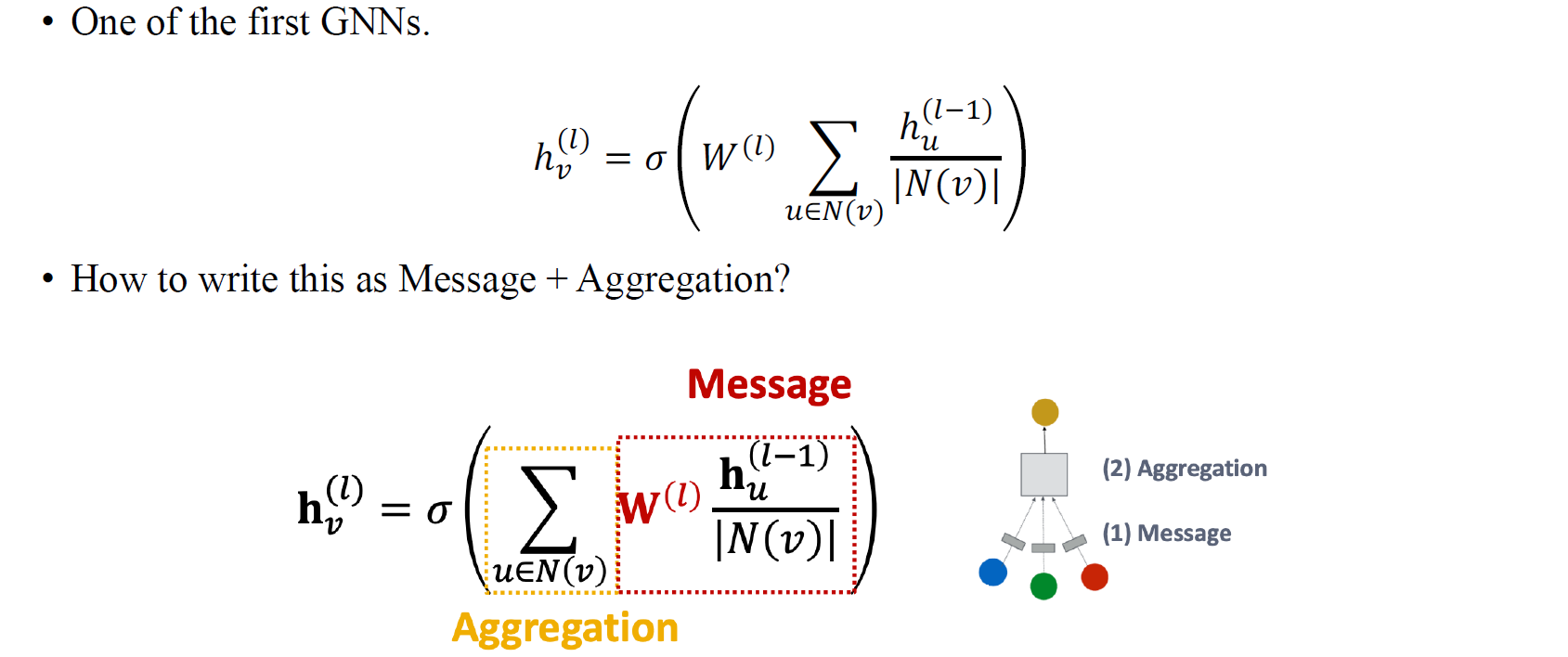지금부터는 여러 GNN framework에 대해서 간략하게만 알아보고자 한다. 가장 먼저 GCN은 message aggregation 구조의 GNN 중 가장 대표적인 사례 중 하나일 것이다. 위의 식에서 빨간 박스가 message computation에 해당하는 부분이고, 노란 박스가 만들어진 message들로부터 aggregation하는 부분이다.

GraphSAGE

GraphSAGE는 aggregation을 무조건 Mean function을 통해서 하지 않아도 된다고 한다. Aggregation에 LSTM과 같은 여러 방법들을 사용해도 좋다는 것이다.

그래서 GraphSAGE는 여러 component들로 구성되어 있다. GCN이 Mean을 통해서 aggregation을 하는 반면에 GraphSAGE는 Mean 외에도 Sum이나 LSTM을 aggregation function으로 사용할 수 있다는 것이다. GraphSAGE는 17년도에 나온 GCN에 이어 18년도에 나온 논문이다. 그래서 GraphSAGE이 GCN의 generalization된 모델임을 확인할 수 있다.

Message Passing Neural Network

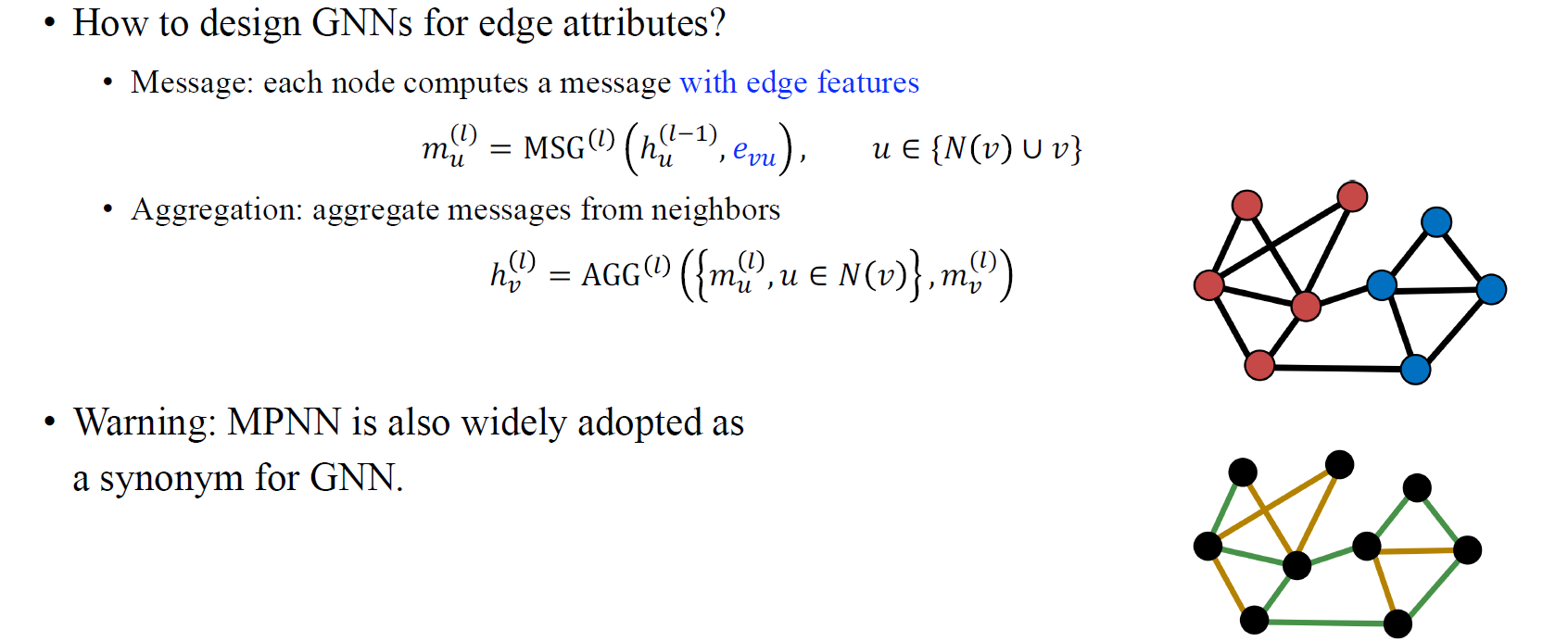다음으로 Message Passing Neural Network (MPNN)에 대해서 알아보고자 한다. 흔히 GNN과 MPNN이 같다고 생각할 수 있어서 이름만봐서는 다소 혼란이 있을 수 있다. 때때로 사람들은 MPNN과 GNN을 같다고 보기도 한다. MPNN이라는 논문이 등장하고 사람들이 MPNN을 이야기할 때는 이는 edge attribute에 대해서 GNN을 설계했다고 보면 된다. MPNN을 message computation에서 edge feature를 통합시키려고 했다. 아이디어가 정말 간단하다. Message를 구할 때 단지 weight matrix를 곱하기보다는 edge feature가 $h_u와 함께 계산되어진다. 이렇게 얻어진 message로 aggregation을 하게 되면 기존의 GCN과 다르게 edge feature를 반영한 결과를 만들 수가 있다.

Relational GCN

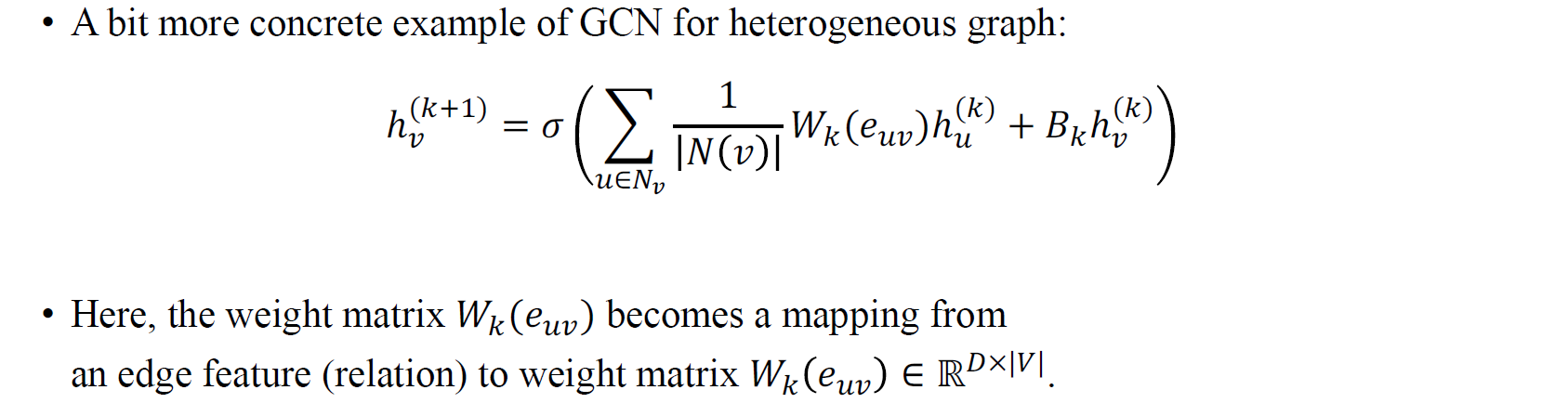다음으로 Relational GCN은 기존의 GCN과 weight matrix에서 차이를 보인다. Heterogeneous graph에 대한 GCN의 특수한 형태로 Relational graph는 edge feature를 weight matrix에 mapping해서 사용하고 있다. Relational graph는 graph의 edge가 categorical한 정보를 담고 있는 경우에 사용하기 위해서 설계된 모델이다. Edge에 서로 다른 값들이 존재해서 서로 다른 class를 형성하고 있는 경우에 적용할 수가 있다. 이러한 categorical feature를 특정 weight matrix에 mapping해서 사용하기 때문에 기존의 GCN에 relation 정보를 반영했다고 볼 수 있다.

CNN as GNN

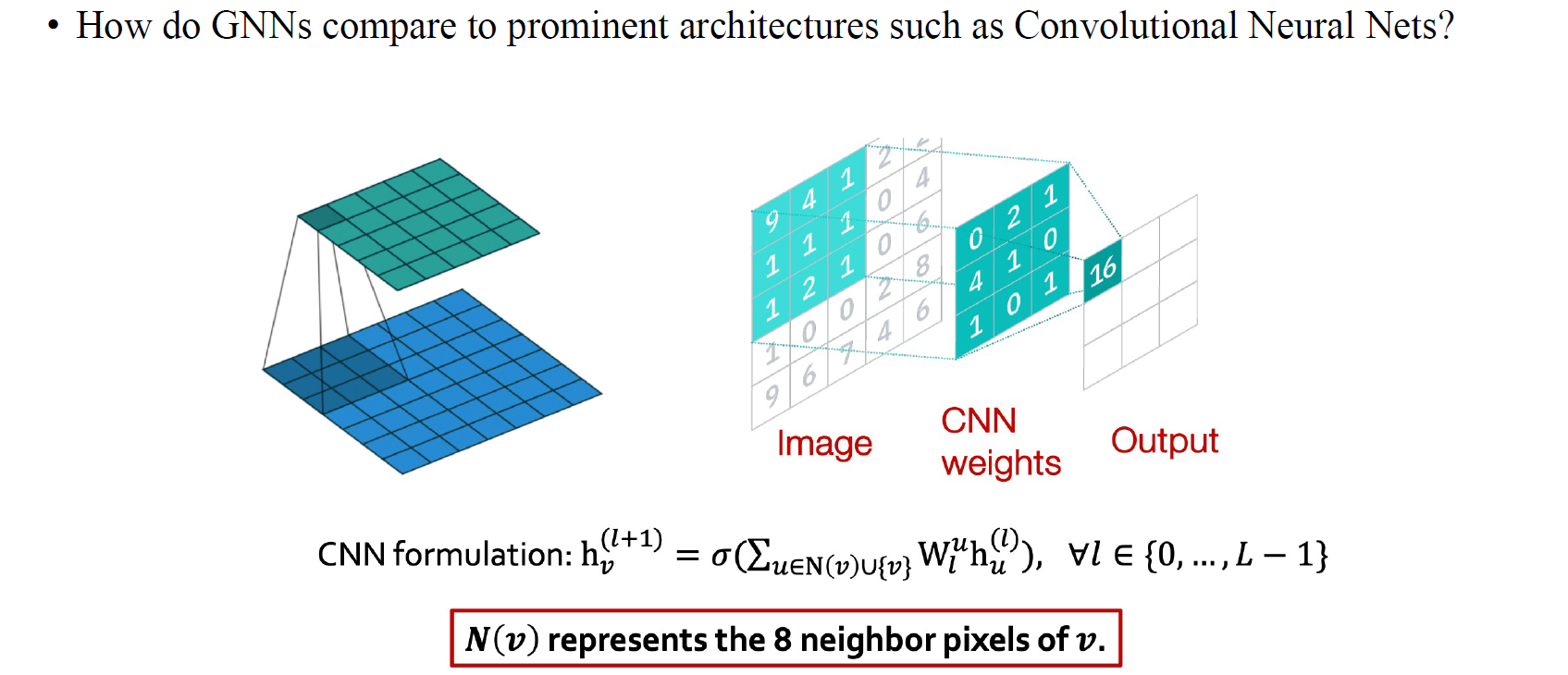마지막으로 GNN을 어떻게 정의할지 설명하고자 한다. 앞서 이야기했듯이 CNN은 결국 GNN의 하나의 경우에 해당하게 된다. CNN은 커널을 사용해서 vertex에 해당하는 주변 pixel들을 보고 message를 전달하게 된다. 이 커널은 픽셀 하나하나에 대응하면서 움직이고, 그럴때마다 커널의 크기만큼의 이웃 vertex들을 보는 것과 같아지게 된다. CNN의 aggregation step에선 이웃 픽셀들을 이용해서 가중합을 구하게 되는데, 이를 GNN에서의 aggregation step으로 볼 수 있는 것이다.

CNN에서는 결국 scalar weight를 각 픽셀마다 적용하여 aggregation을 한다고 보면 된다. Multi dimensional한 경우에 대해서는 각 픽셀마다 채널만큼의 feature가 있기 때문에 weight를 통째로 곱할 수가 있다. 즉, CNN에서는 weight matrix가 채널의 차원만큼 늘어나 곱해지게 될 것이라는 이야기이다. Graph에서 node feature가 픽셀의 채널과 같다고 생각할 수 있는 것이다. CNN에서는 $W_1,W_2,\dots$ 등이 모두 다른 값을 가지게 될 것이지만, GNN에서 weight를 동일하게 사용한다. 이 부분이 CNN과 GNN의 차이점이다. GNN은 edge들이 동일하게 사용되기 때문에 모든 weight를 공유하지만, CNN은 픽셀마다 다른 이웃들을 보기 때문에 서로 다른 weight를 사용하게 된다.

CNN은 2D grid에서 이웃 픽셀 개수가 8개로 정해져있는 GNN의 특수한 경우이다. 그리고 이웃 픽셀마다 weight가 고정되어 있지 않고 미리 정의된 크기의 커널을 사용하게 된다. GNN의 이점 중 하나가 바로 node가 얼마나 있고 어떠한 형태로 graph를 형성하든지간에 weight가 결국 고정될 수 있어 쉽게 학습할 수 있다는 것이다. 그리고 graph의 node feature의 차원과 image의 채널 차원이 동일하다. 이러한 점들 때문에 CNN이 GNN의 부분집합처럼 설명될 수 있는 것이다. 그리고 중요한점 중 하나가 CNN은 GNN과 다르게 permutation invariant하거나 equivariant하지 않다는 점이다. 아무래도 2D grid에 픽셀의 위치가 정해져있기 때문에, 만약 픽셀의 순서가 달라질 수 있다면 원하는 결과와 다른 결과가 만들어질 수도 있을 것이다.