[그래프 기계학습] Graph Signal Processing 1

Why Signal Processing?

이번에는 GNN을 signal processing의 관점에서 다시 끌어내보려고 한다. 새로운 GNN 구조를 만든다고 했을 때 사람들은 CNN에서 이미지 상에 잘 동작했던 것을 어떻게 하면 GNN에 가져다가 사용할 수 있을지를 주로 고민하곤 한다. 그래서 사람들은 항상 GNN 구조를 generalization하는 것에 관심이 많으며 이는 signal processing 분야와 관련해서 중요한 부분이다. 실제로는 signal processing 자체는 굉장히 오래된 분야이지만, 아직 graph signal processing 분야는 많이 확립되었다고 보기 어렵다.

Signal processing은 전기전자 분야에서 굉장히 널리 알려진 개념 중 하나이다. 대표적인 예시로 time singal을 생각해볼 수 있으며, time signal은 time $t$에 정의되는 function이다. 가령 time series data에서는 기본적으로 time signal이 고려되었다. 또한 이미지도 signal data로 볼 수 있다. 대신 Euclidean coordinate에서 $x$와 $y$에 의해 정의되는 2d signal인 셈이다. Image signal processing의 대표적인 사례로는 blurring된 image를 떠올릴 수 있을 것이다. 여기서 blur를 지워 원래의 image를 복원하는 것도 signal processing의 관점에서 해결할 수 있는 문제이다. 결국 CNN이나 이미지를 다루는 neural network도 signal을 processing하기 위해서 만드는 것과 다름이 없다. 우리가 data를 vector로 표현하지만, 이러한 vector에는 index로 mapping 되는 특정 위치가 존재하고 이로부터 signal로 표현이 되기 때문에 결국 어떠한 data도 signal로 표현이 가능하다. 대표적으로 input으로 image의 $x$와 $y$의 coordinate를 넣어주면 이에 대응되는 RGB color를 output으로 내는 function을 구할 수 있을 것이다.

Signal processing에서 중심이 되는 operation은 바로 convolution이다. 우리는 이번에 얼마나 convolution이 흥미로운지 알아볼 것이고, 이 개념을 확장해서 graph convolution까지 어떻게 연결이 되는지 알아보고자 한다. CNN이라는 개념이 image data에 대해서 존재하기에 이를 확장해서 graph CNN, 즉 graph convolution에 대해서 알아볼 것이다. 결국 graph convolution을 이해하기 위해서는 graph signal processing (GSP) 분야를 확실히 하고 가야한다.

The Big Picture

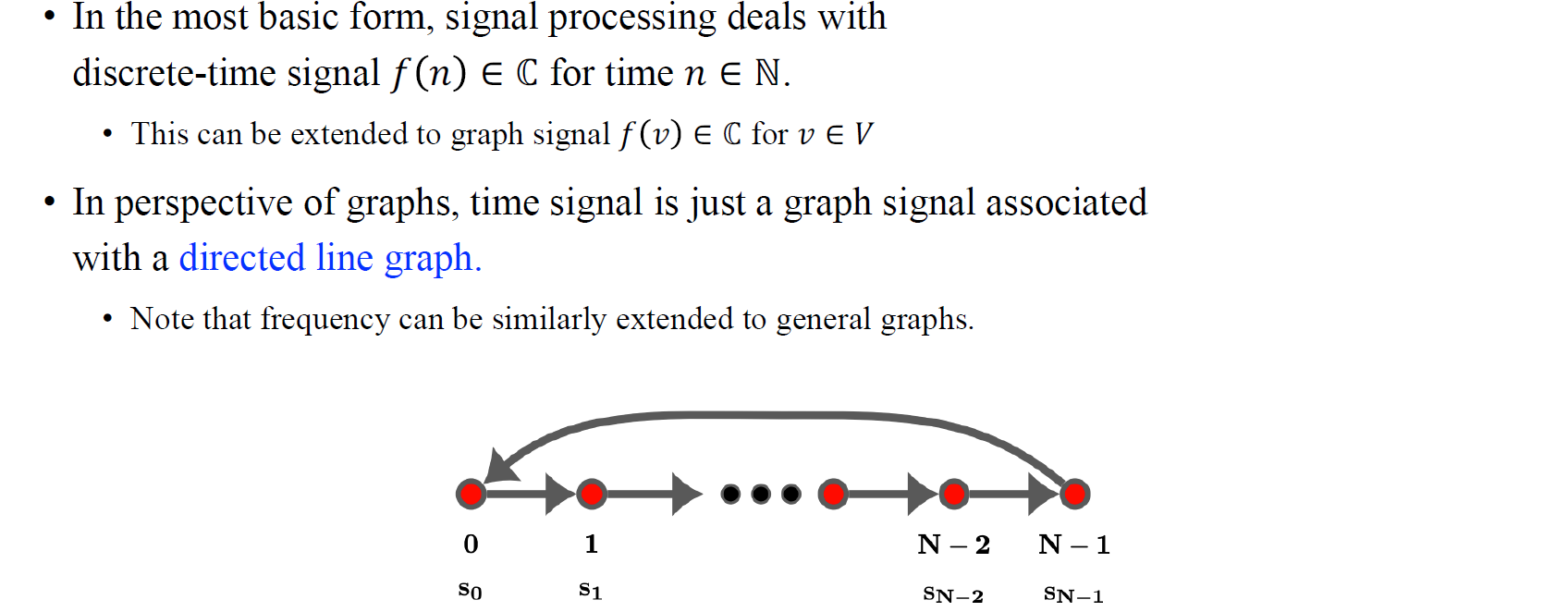딱 한가지만 기억해야 한다면 결국 우리는 graph domain에 convolution을 generalization할 수 있다는 것이다. 이를 위해서 간단한 directed line graph를 이용해서 설명하고자 한다. Time signal은 1차원에서 정의되는 1D signal인데, 이를 graph domain에서 directe line graph에 적용해보면 vertex마다 연결되는 방향성이 존재하는 edge가 있기에 이를 따라서 vertex를 discrete time으로 보고 같은 1D signal로 해석해볼 수 있게 된다. Time $n$에 따른 discrete-time signal $f(n)$이 $v$개의 vertex를 가지는 graph signal $f(v)$로 확장될 수 있다는 것이다.

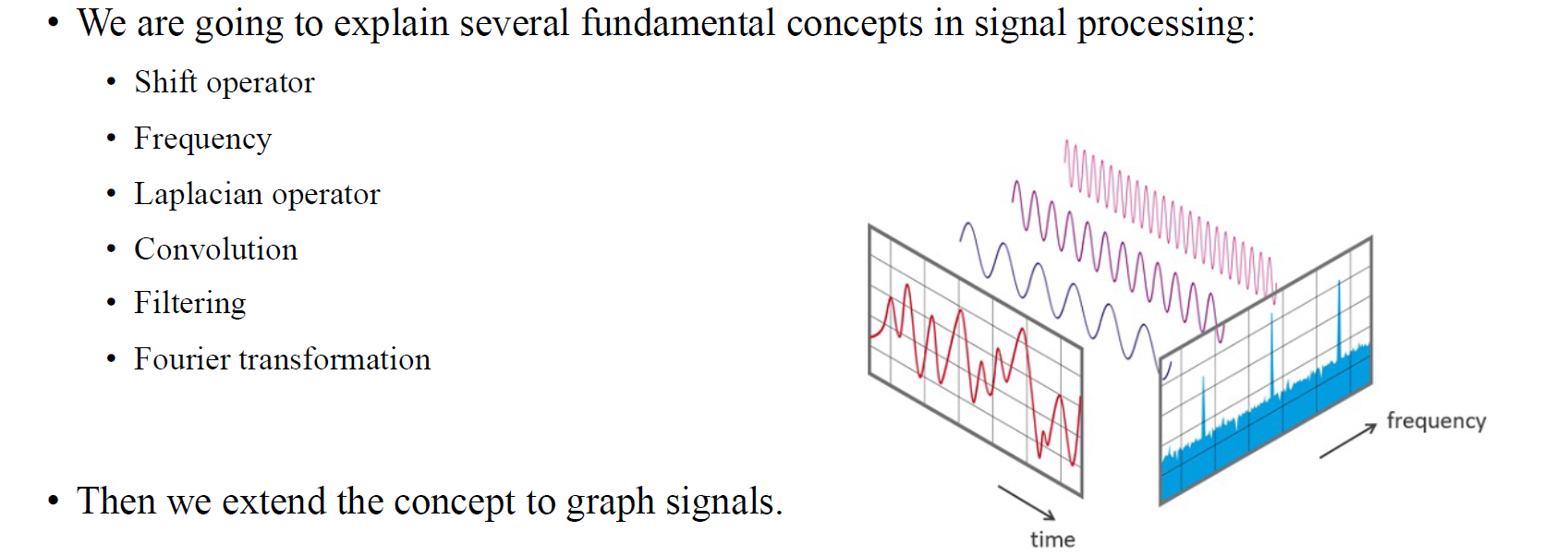우리는 line graph에서 GSP를 정의할 것이고, line graph에서의 GSP는 결국 time signal에서의 signal processing이 될 것이다. 그래서 우리는 GSP와 signal processing 사이에서의 connection을 만들고자 하며, 이를 위해 먼저 frequency와 같은 signal processing에서 이미 알고있는 용어들을 다시 정의하고 시작할 필요가 있다. GSP에서 조금 더 직관적으로 이해하기 위해서 이러한 과정들이 필요할 것이다.

우리는 signal processing에서 여러 근간이 되는 개념들을 알아볼 것이고, 비록 signal processing 자체가 engineering의 영역이라고는 할지라도 개념 자체는 꽤 직관적이고 수학적으로도 많이 알려져있기 때문에 그렇게 어렵지는 않다. Shift, frequency, lapalcian operator, convolution, filtering, fourier transformation 등 여러 개념들이 등장하기에 이를 하나씩 살펴볼 것이고, signal processing에서의 개념으로부터 시작해서 GSP까지 연결시켜볼 것이다.

Time Signal as Graph Signal

Time signal의 특징 중 하나는 이것이 여러개의 function으로 분해될 수 있다는 것이다. 즉, time signal이 여러 작은 periodic signal로 분해되어 summation의 형태로 표현될 수 있다. 이로부터 signal processing이 분해된 function $f(1),f(2),\dots,f(T)$들을 다루고, 여기서 각 function $f$는 constant frequency로서 정의 될 수 있다. 예를 들어 $f(1)$은 느리게 흔들리는 frequency이고 $f(2)$는 이보다 빠르게 흔들리는 frequency로 정의할 수 있다는 것이다. 우리는 결국 전체 signal로부터 infitine하거나 finite한 여러 signal들로 분해할 수 있다.

이러한 시간에 대한 function인 time signal이 graph signal로서 표현될 수 있게 된다. 이를 이해하기 위해서 먼저 discrete signal processing에서부터 시작해서 시간이 discrete하다는 가정을 할 것이다. 물론 이러한 discrete한 시간을 합치면 전체 시간이 될 것이다. 그리고 time signal이 period $T$에 따른 periodic function이라는 또 하나의 가정을 해볼 것이다. 그러면 우리는 time signal을 시간으로부터 어떠한 output으로 매핑되는 vector ${\bf f}$로 표현할 수 있을 것이다. 사실 time signal이 graph signal로 정의가 되는 것은 굉장히 흥미로운 부분이다. Time이라는 개념은 어떠한 integer는 아니지만 integer들이 set을 이루고 방향성을 가지게 되면 성립이 되는 구조이다.

그렇다면 시간 사이에 sequential relationship과 같은 이러한 개념을 어떻게 정의하면 될까? 우리는 adjacency matrix $A$와 같은 linear operator를 이용해서 정의할 수 있다. 여기서 $A$를 우리는 shift operator라고도 부를 수 있다. 이는 시간의 흐름에 따라 어떻게 signal이 행동하는지에 대해서 설명할 수 있다. 예를 들어, periodic function $f(T)$와 $f(T+1)$이라는 2개의 함수가 있다고 했을 때, 뒤의 함수는 linear operator $A$를 앞의 function에 적용시켜서 만들 수가 있다. $A$를 1과 0으로 잘 구성하면 $f$의 원소 순서를 바꾸는 shift 연산이 적용되는 효과가 발생해서 결국 같아지게 만들 수 있다는 것이다.
우리는 이렇게 $f$라는 function을 graph signal로도 볼 수 있으며, time에 mapping된 function이 아닌 vertex에 mapping된 function으로 볼 수 있고, $f(1)$부터 $f(T)$까지 shift 연산이 adjacency matrix를 곱하는 것과 일관성이 있게 된다. 따라서 시간으로부터 real number로 mapping되는 time signal이 같은 맥락으로 vertex에서 real number로 mapping되는 graph signal로 정의될 수 있다는 것이 중요하다. 그리고 $f(T)$와 $f(T+1)$ 사이의 progression이나 relationship은 matrix multiplication으로 표현될 수 있다. 여기서 matrix는 directed graph에서의 adjacency matrix가 될 것이다.

Frequency

우리는 지금까지 time signal이 무엇인지와 time signal의 progression을 정의 했다. 2개의 function 사이의 relationship을 예로 들어 progression을 설명했었다. 지금부터는 signal의 frequency가 무엇인지를 알아보고자 한다. Signal processing에서는 만약 특정 signal이 periodic하다면, 우리는 frequency를 period의 inverse로 정의할 수 있다. 하지만 signal이 불규칙한 모양을 가지고 있을 때도 많을 것이다. 이러한 경우에는 전체 signal의 frequency를 정의하기 어려워진다. 그래서 signal의 파동으로 frequency를 정의하고 싶다면, 우리는 signal이 특정한 형태를 가진다고 가정할 필요가 생긴다.

우리는 frequency를 정의하기 위해서 distcrete Fourier series가 무엇인지 알아야하며, discrete Fourier series element 혹은 discrete Fourier bases에 대해서 알아야 한다. Discrete Fourier series element는 $f(n)=e^{i\frac{2\pi kn}{N}}$으로 정의할 수 있다. 그리고 Euler's formula에 의해서 exponential function을 cosine function으로 생각할 수 있다. 이렇게 정의된 element는 단지 규칙적으로 파동을 형성하는 성질을 지니고 있다.

만약 이렇게 특별한 형태를 가정하게 되면 우리는 $f(n)$과 frequency사이에 흥미로운 관계를 찾을 수 있다. Cosine의 period는 $2\pi$이기 때문에 위와 같이 $f(n)$을 가정하게 된다면 $kn$을 $N$으로 나누는 최소 $n$이 해당 function의 period가 된다. 그러면 우리는 여기서 $k$를 frequency로 부를 수 있다. 왜냐하면 $cos(kx)$를 생각해보면 $k$가 증가함에 따라 훨씬 많이 파동을 일으킬 것이기 때문이다. 따라서 discrete time signal에서 $k$를 frequency으로 볼 수 있게 되었고, 적어도 $k$ 자체가 frequency와 관련이 있는 부분이 될 것이다.

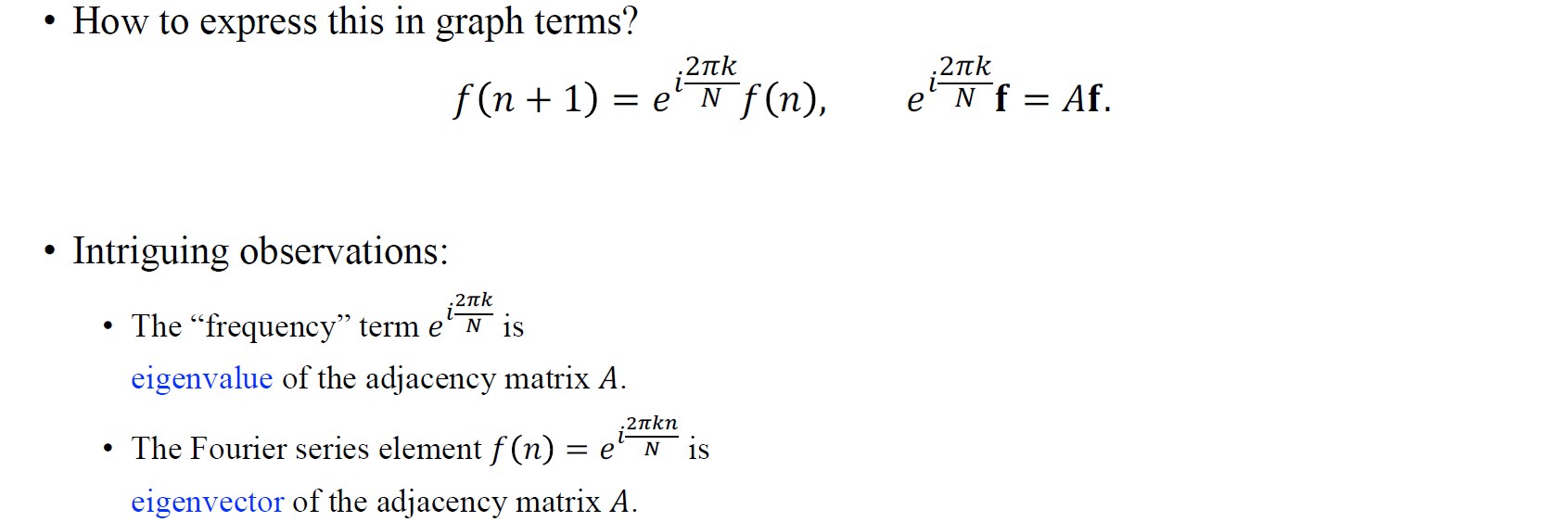한가지 더 흥미로운 점은 우리가 만약 위와 같이 signal을 특별한 형태로 가정하게 된다면 $n$을 time $T$라고 했을 때 time의 progression을 $Af$로 볼 수 있게 된다. 또다른 relationship으로 우리가 특수한 Fourier series element를 가정하게 된다면, 우리는 $f(n+1)$을 $f(n)$에 어떠한 constant를 곱한 형태로 표현할 수 있게 된다. 여기서 constant는 $k$값에 의존하게 될 것이다. 이러한 Fourier series element에 따라서, time의 progression은 어떠한 값들의 곱의 형태로 표현될 수 있으며, 여기서 어떠한 값들은 frequency $k$에 따라 달라지게 된다. 만약 $k$가 커진다면 time progression에 따라 function이 더 빠르게 변할 것이다.

우리는 이러한 relationship에 대해서 알아보았는데, 이와 더불어서 어떠한 constant와 vector $f$를 곱한 결과가 time의 progression을 나타내는 shift operator 혹은 adjacency matrix $A$와 $f$를 곱한 결과와 같다는 관계도 얻을 수 있다. 여기서 흥미로운 점은 $k$에 따라 달라지는 frequency term $e^{i\frac{2\pi k}{N}}$이 adjacency matrix $A$의 eigenvalue라는 것이다. 그리고 Fourier series element $e^{i\frac{2\pi kn}{N}}$은 shift matrix $A$의 eigenvector에 해당하게 된다. 이는 graph의 관점에서 Fourier transform을 생각했을때 흥미로운 부분이다.
여기서 eigenvector와 eigenvalue로 연결되는 점이 의미하는 것은 무엇일까? $A$의 eigenvector는 어떠한 matrix를 생각해보면 우리가 $A$를 여기에 적용했을 때 방향이 변하지 않는 vector를 의미한다. $A$를 $f$에 적용했을 때 identity가 변하지 않아야 eigenvector인 것이다. $A$는 shift operator으로 time을 shifting하거나 vertex를 permuting하게 만들 것이다. 따라서 eigenvector의 개념은 equivariance의 개념과 관련이 있는 것이다. 다시 정리해보면 $A$를 곱하는 것은 time을 shifting 하겠다는 것이고, Fourier series element에 대해서 frequency term은 특정 signal $f$의 eigenvalue로 볼 수 있다.

Laplace Operator

우리는 Fourier series element $e^{i\frac{2\pi k}{N}}$를 특정 function으로 선택했었다. 그렇다면 이러한 fucntion이 왜 특별할까? 우리는 다른 basis 혹은 다른 element로부터 frequency를 정의할 수 있다. 그리고 이로부터 또한 흥미로운 relationship을 마찬가지로 얻을 수 있을 것이다. 하지만 우리가 이러한 fucntion을 선택했던 것은 이는 Laplace operator와 직접적인 관련이 있고, 이는 추후에 graph Laplacian과 연결될 것이기 때문이다. 사람들은 이러한 Fourier series로부터 1차원 Laplace operator의 eigenfunction으로 얻어지게 된다는 것을 발견했다. 위의 식에서 $\Delta$가 Laplace operator이다. Fourier series는 이후에 harmonic function으로서 일반화되며, harmonic function은 eigenvalue가 0에 대응되는 Laplace operator의 eigenfunction에 해당하게 된다. 여기서 harmonic function은 Laplace operator를 적용했을 때 그 결과가 항상 0이되는 function을 의미한다. 디테일한 내용은 생략하고 여기서 알아야하는 것은 바로 사람들이 Fourier series를 Laplace operator의 eigenfunction으로 얻었다는 것이다. 이후에 이러한 graph Laplacian으로 어떻게 연결되는지 설명할 것이다.

Graph Laplacian

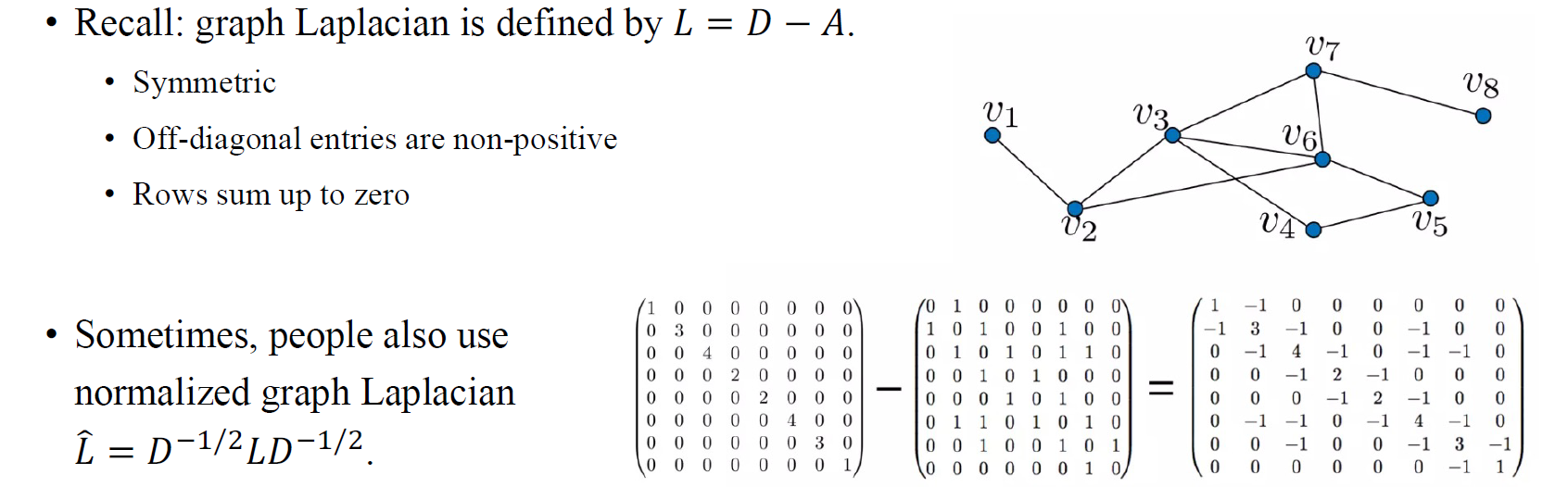Graph Laplacian은 degree matrix $D$에서 adjacency matirx $A$를 뺀 $L$로서 정의가 된다. $L$의 특징은 symmetirc하고 off-diagonal entry들이 non-positive하며, row를 전부 더하면 0이 된다는 것이다. 그리고 사람들은 degree에 대해서 normalization을 한 normalized graph Laplacian $\hat L$을 사용하기도 한다.

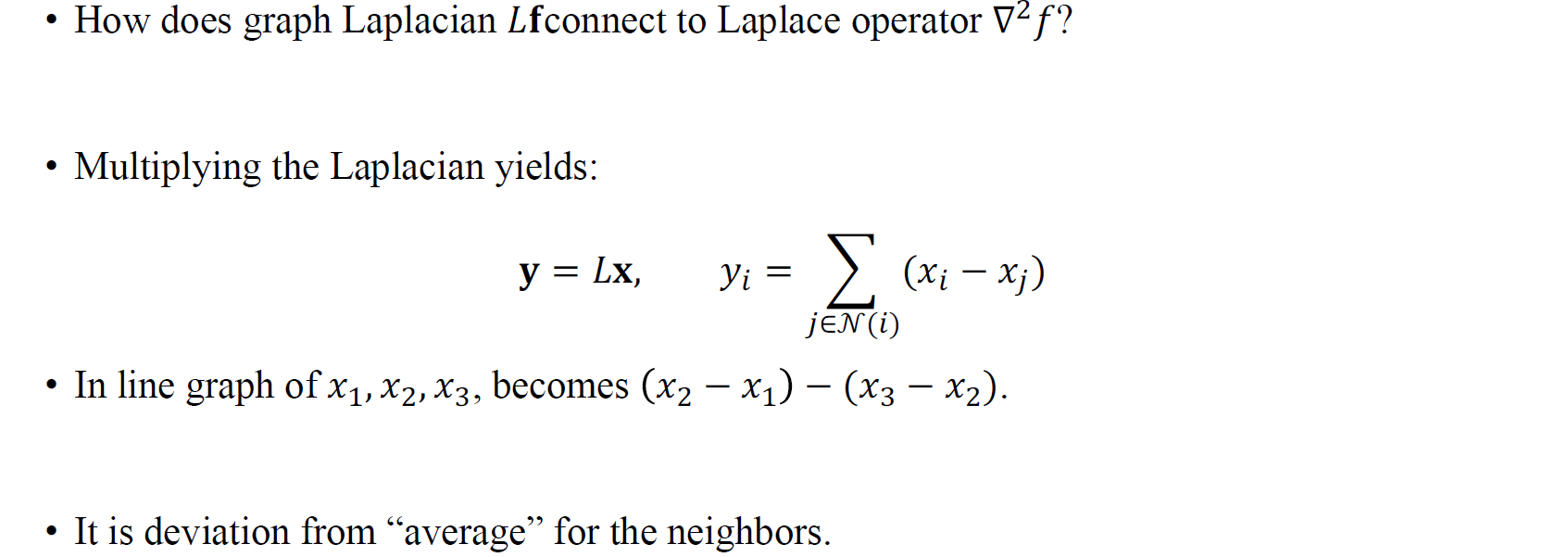여기서 주목해야하는 점은 어떻게 function $f$에 graph Laplacian $L$을 곱한 $Lf$가 Laplace operator를 function에 곱한 $\Delta f$와 연결이 되는지이다. Laplacian matrix $L$을 어떠한 vector $x$에 곱했을 때 생기는 relationship으로 얻어진 새로운 signal $y$의 $i$번째 element $y_i$는 $x_i$와 이웃한 $x_j$를 뺀 것의 합으로 만들어진다는 것이다. 예시로 $x_1,x_2,x_3$의 line graph에서 $(x_2-x_1)-(x_3-x_2)$는 결국 시간에 대한 derivative로 직관적으로 이해될 수 있을 것이다.

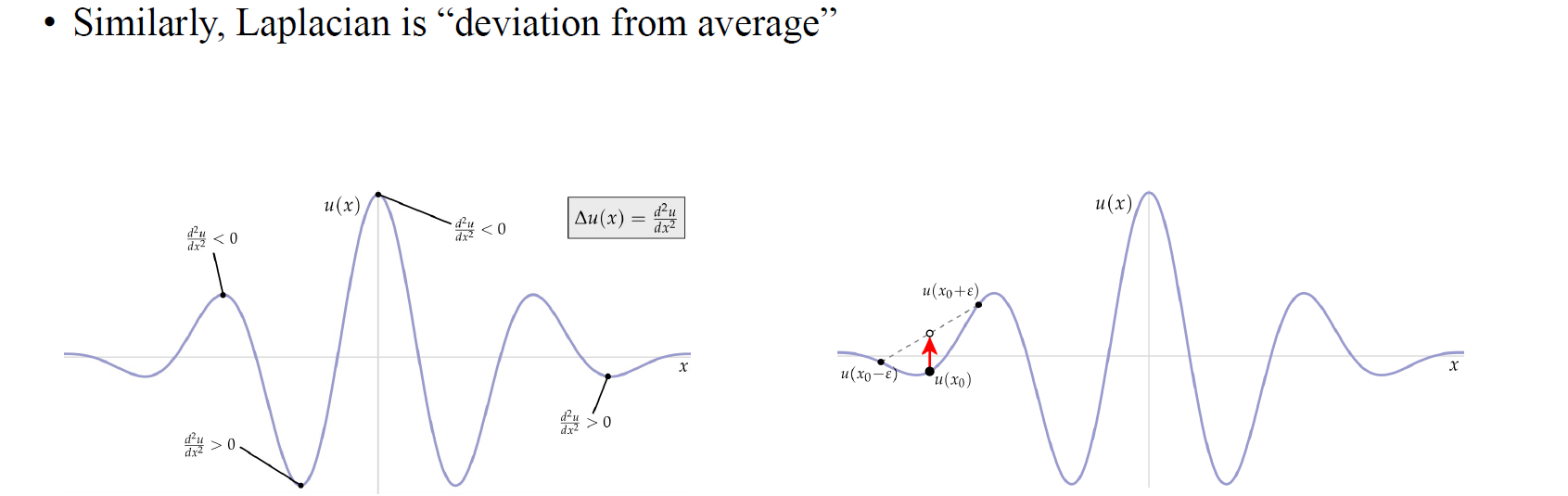이런식으로 Laplacian은 결국 neighbor에 대해서 "deviation from average"로 볼 수 있다. Vertex $i$가 있다고 하면 이에 대응하는 neighbor들이 있을 것이고, 이들의 평균을 구하고 이를 neighbor들과 비교해서 더해볼 수 있을 것이다. 이러한 정의가 결국에는 더 일반적인 경우에 대해서도 사람들이 흔히 부르는 Laplacian이 될 것이다.
그렇다면 어떻게 구할 수 있을까? 사람들은 Laplacian operator를 Euclidean space에서 curvature로 부르기도 한다. 우리는 time signal 혹은 1D signal에서 Laplacian을 구할 수 있을 것이고, 만약 Laplace value가 0보다 작으면, derivative가 positive에서 negative로 바뀌기 때문에 signal이 볼록한 형태를 보일 것이다. 반대로 derivative가 negative에서 positive로 바뀌게 된다면 Laplace value는 0보다 크게 될 것이다.

이러한 현상을 보는 다른 관점은 우리가 하나의 값을 선택하고, 아주 작은 $\epsilon$을 더하고 빼서 선택한 값의 주변을 보는 것이다. Laplace value 혹은 Laplace operator를 적용한 결과는 만약 이웃들의 평균을 내어 그 값이 선택된 지점보다 크게 된다면 positive일 것이다. 주변 neighbor로부터 선택한 지점과의 차이를 평균내다보면 대략적으로 curvature 혹은 continuous signal에서 정의되는 Laplace operator에 근사하게 될 것이다. 결국, Laplacian value를 이와같이 "deviation from average"로 생각하는 것이 이해하기에는 더 쉬울 것이다.

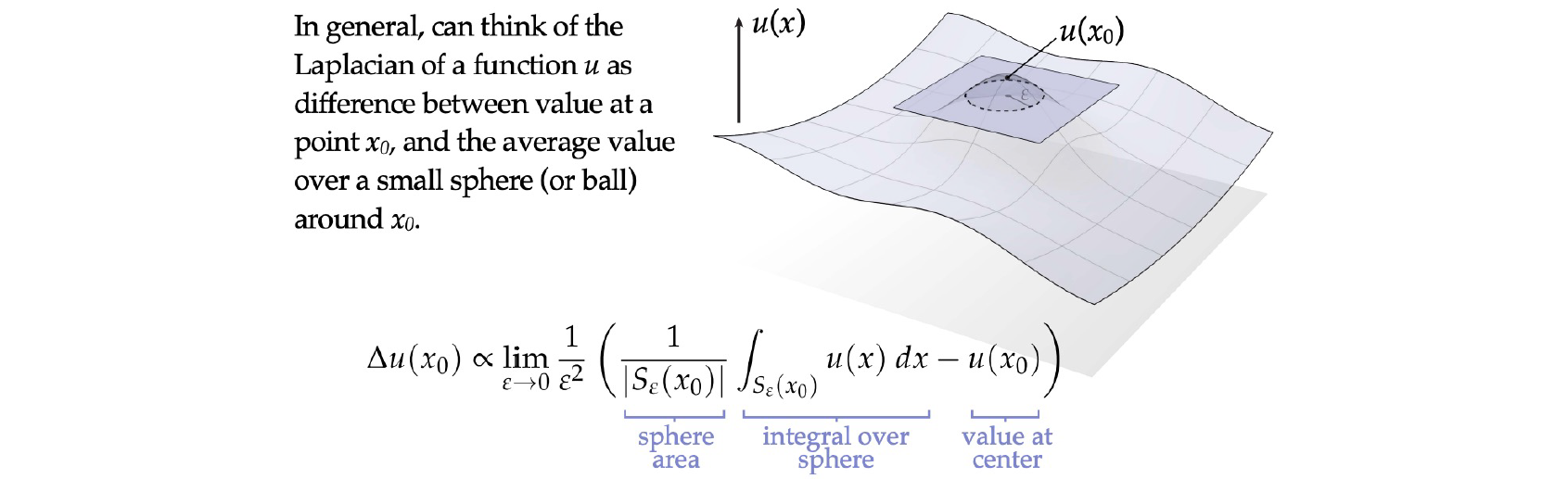위의 사진은 Laplacian function의 general한 경우를 보여주고 있다. 여기서 function $u$의 Laplacian을 특정 point $x_0$와 $x_0$ 주변의 작은 sphere의 평균 사이의 difference로 생각할 수 있는 것이다. 이 값이 positive인지 negative인지에 따라 curvature가 결정되는 것이다.

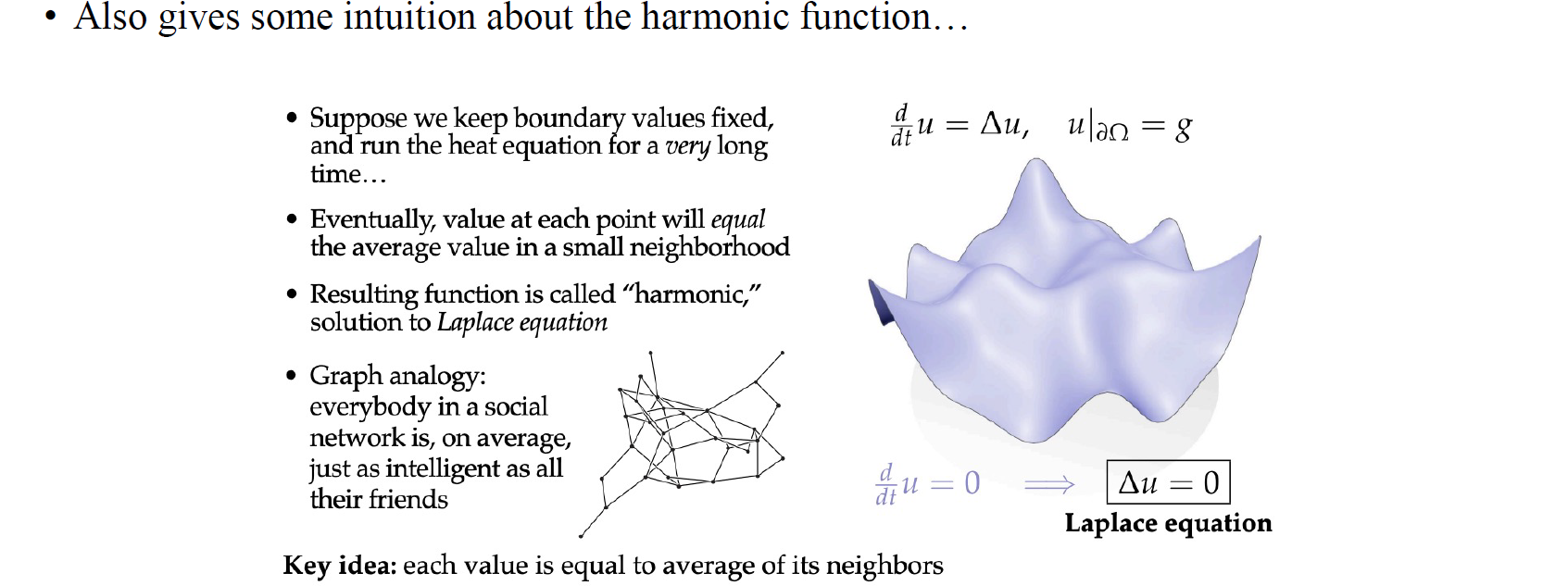이는 $u$의 Laplacian opreator가 0이 되는 harmonic function과 관련해서 흥미로운 점을 제공해준다. Harmonic function에서 하나의 지점을 선택했을 때, 이는 대략적으로 주변과 비슷할 것이다.

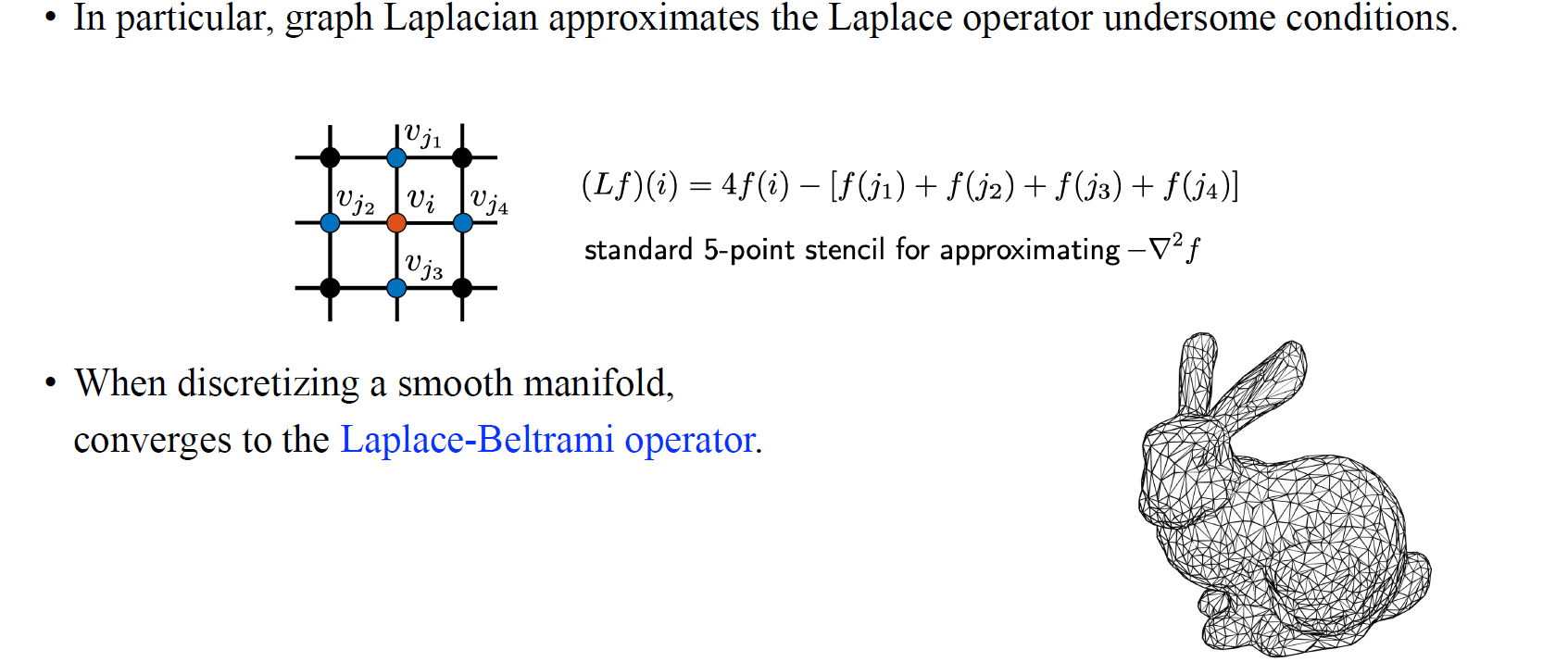우리가 3D 물체를 descretization을 한다고 했을 때, $D-A$로 정의되는 graph Laplacian operator $L$은 limit를 infinity로 취한다면 실제 continuous Laplace operator과 일치할 것이다.

정리해보면 결국 Fourier basis가 Laplace operator의 eigenfunction으로 유도되어 져서 $\Delta f = \lambda f$로 정의가 된다. 여기서 $f$는 discrete time의 경우에 대해서 eigenfunction 혹은 eigenvector가 될 것이다. 이로부터 우리는 Laplace matrix의 eigenvector를 비슷하게 정의할 수 있었고, 이는 $Lf=\lambda f$로 정의가 된다. 그리고 여기서의 $f$는 graph Laplacian의 eigenvector가 될 것이고, 이는 graph signal processing에서 새로운 Fourier basis가 될 것이다.