[그래프 기계학습] Graph Signal Processing 2

Alternative Fourier Basis

우리는 time signal에 대한 shift operator로 여겨지는 adjacency matrix에 대해서 알아보았고, degree matrix에서 adjaency matrix를 빼서 만들 수 있는 Laplacian matirx $L$에 대해서 살펴보았다. 그리고 Fourier basis가 $A$ 혹은 $L$의 eigenvector로 유도가 되는 것을 알 수 있었으며, 2가지 경우의 eigenvector가 모두 유효한 signal processing을 정의할 수 있었다. 사람들은 $A$의 eigenvector가 Fourier basis element로 사용해야 하며, $L$의 eigenvector는 graph signal의 Fourier basis로 사용해야한다고 말하며 구분해야 한다고 하지만 아니라고 할 수도 있다. 사실 우리는 특정 time signal line graph에서는 두가지 정의가 같을 수 있지만, 일반적인 graph에서는 두가지 정의가 다름을 입증할 수 있다. 사람들은 $A$의 eigenvector를 graph signal에서 Fourier basis로 사용하기도 하며, 그렇지 않은 경우에는 $L$의 eigenvector를 graph signal에서 Fourier basis로 사용한다. 우리가 하고자 하는 것은 결국 eigen decomposition을 통해서 eigenvector를 얻고, 이로부터 basis를 바꾸고자 하며, vector $f$는 coefficient와 eigenvector들의 곱들의 summation과 같도록 표현하고자 한다. 이는 이후에 설명할 Fourier transformation과 관련이 있다.

Smoothness

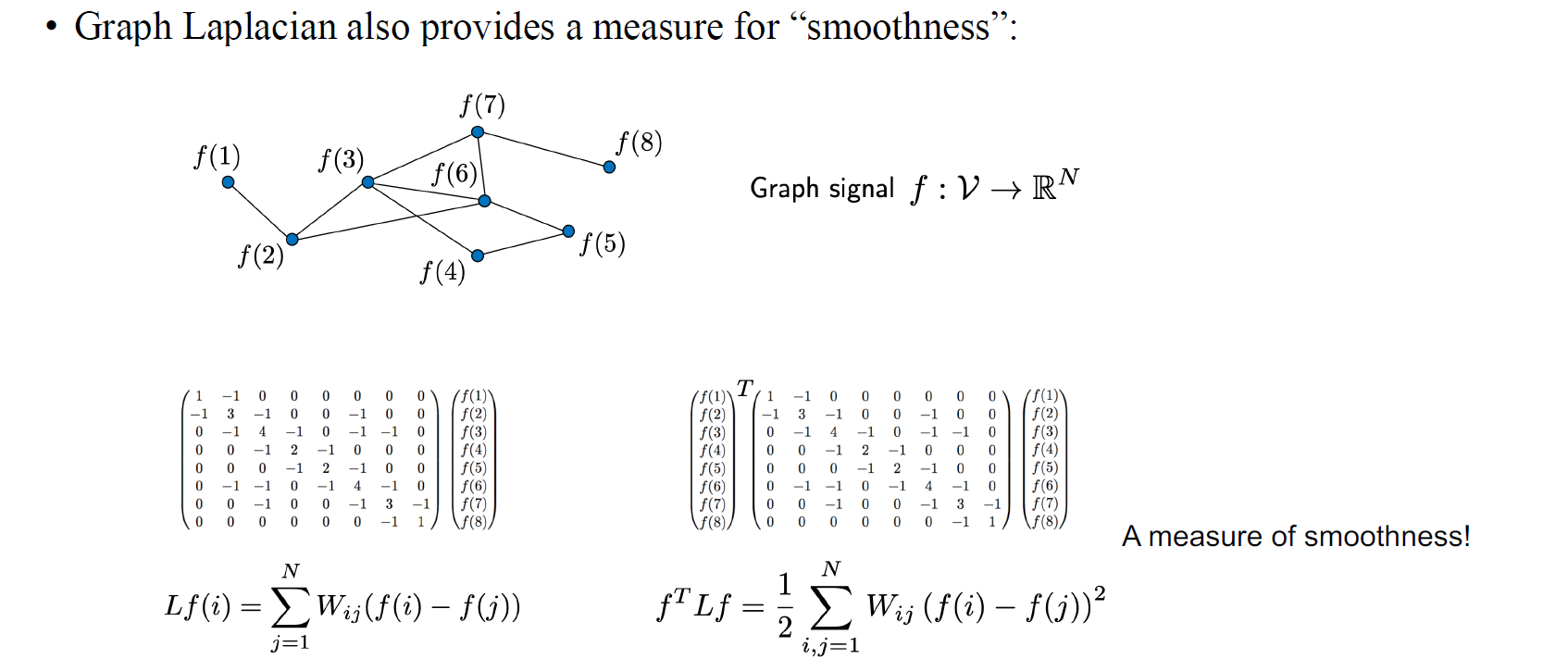마지막으로 Graph Laplacian은 특정 function $f$의 smoothness라는 것을 측정하는 도구로서 사용이 될 수 있다. 만약 우리가 $L$에 $f$를 양옆으로 곱하게 된다면, 위와같이 $f(i)-f(j)$의 제곱의 summation으로 표현이 되고, 이로부터 우리가 smoothness를 측정할 수 있게 될 것이다. 이는 이웃한 vertex들과의 차이를 측정할 수 있어서, 이로부터 smoothness를 구하게 되는 것이다. 이 식이 이상해보일 수 있지만, 여기서 $W_{ij}$는 0 아니면 1이 된다. 1이라는 것은 $i$와 $j$ 사이에 edge가 존재한다는 것이다.

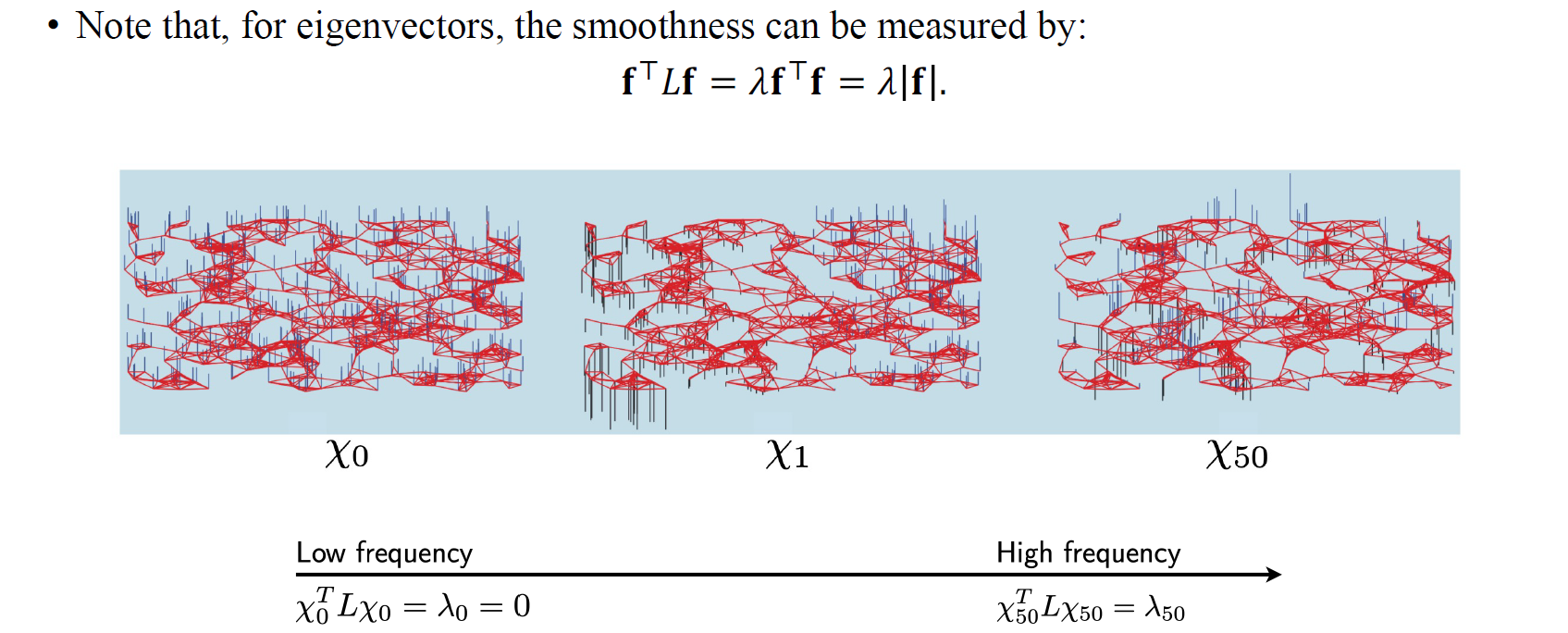또 다른 흥미로운 부분은 Laplacian matrix의 eigenvector를 통해서 smoothness를 구할 수 있다. 우리는 위와 같이 $f^TLf$에서 $\lambda f^Tf$를 얻게 된다. 결국 우리는 smoothness를 구하기 위해서 $f^TLf$를 구했지만, 여기서 최종적으로 frequency term $\lambda$와 관련된 식을 유도하게 된다. 그리고 이 $\lambda$는 eigenvector의 norm인 $|f|$와 곱한 형태가 된다. 우리는 function이 심하게 파동을 일으키면 smooth하지 않음을 알고있다. 여기서 얻을 수 있는 relationship으로는 $\lambda$가 커지면 커질수록 $f$가 더 심하게 요동치게 된다. 가장 작은 frequency term으로 $\lambda$가 가장 작은 경우에는 대응되는 eigenvector가 굉장히 smooth하지만, 그 값이 커지면 커직수록 대응되는 eigenvector가 심하게 파동을 보여주게 된다.

정리해보면 우리는 $f$를 $L$의 2번 곱해서 node feature간 difference를 제곱한 값을 얻게 되었다. 이 결과가 작으면 작을수록 이웃한 node와의 유사도가 올라가는 의미를 갖게 되기 때문에 연결된 node까리 유사하게 만들고 싶으면 $f^TLf$를 최소로 만드는 $f$를 구하면 될 것이다. 여기서 $f^TLf$이 결과적으로는 $f$의 smoothness 혹은 frequency를 의미하게 되는데, 이 값이 커지게 되면 signal간 difference가 커져 결국 high frequency를 지니고 있다고 해석할 수 있고, 반대로 difference가 작아지면 low frequency를 지니고 있다고 볼 수 있다. 우리는 low frequency의 영역이 중요함을 알기에 $f^TLf$를 최소로 하는 $f$를 구하고자 하며, 결과적으로 최적의 $f$를 구해보면 $L$의 eigenspace에 속하는 eigenvector가 여기에 해당하게 될 것이다. 결과적으로 eigenvalue $\lambda$는 이에 대응하는 eigenvector $f$의 smoothness를 의미하게 되고, 가장 작은 $\lambda$에 대응하는 eigenvector가 가장 smooth한 vector가 될 것이다. 우리는 결국 smoothness를 eigenvalue로 측정할 수 있는 것까지 알게 되었다.

Fourier Transformation

Fourier transform은 어떠한 function $f$를 Fourier series로 분해하기 위한 coefficient들을 구하는 과정을 일컫는다. 우리는 $f$로부터 coefficient와 이에 대응되는 basis function 혹은 eigen function을 구해 분해하고자 하는 것이다. 한편, Fourier transformation이 있다면 역과정인 inverse Fourier transformation도 존재한다. Fourier transformation이 기존의 function을 coefficient의 set 혹은 새로운 basis에 관한 새로운 coordinate로 분해하는 과정이라면, inverse Fourier transformation은 Fourier series element와 곱해지는 coefficient 분해했던 Fourier transformation을 역으로 수행하여 다시 원래의 function을 구성하는 과정이다. 요약하면 Fourier transformation은 signal에서 coefficient로, inverse Fourier transformation은 coefficient에서 signal로 전환하게 된다.

우리가 Fourier transformation과 inverse 과정을 matrix의 관점에서 이야기하게 되면 vector $f$를 eigen vector를 모아놓은 matrix $U$를 basis로하여 분해할 수 있다. Basis matrix를 바꿔주도록 matrix multiplication을 통해서 수행할 수 있다는 것이다. Fourier coefficient들을 모아놓은 $\hat f$를 다시 $U$와 곱해주면 원래의 signal $f$를 만들 수 있다. $f$에 $U$를 곱해주면 Fourier transformation이 되고, $\hat f$에 $U^T$를 곱해주면 inverse Fourier transformation이 되는 것이다.

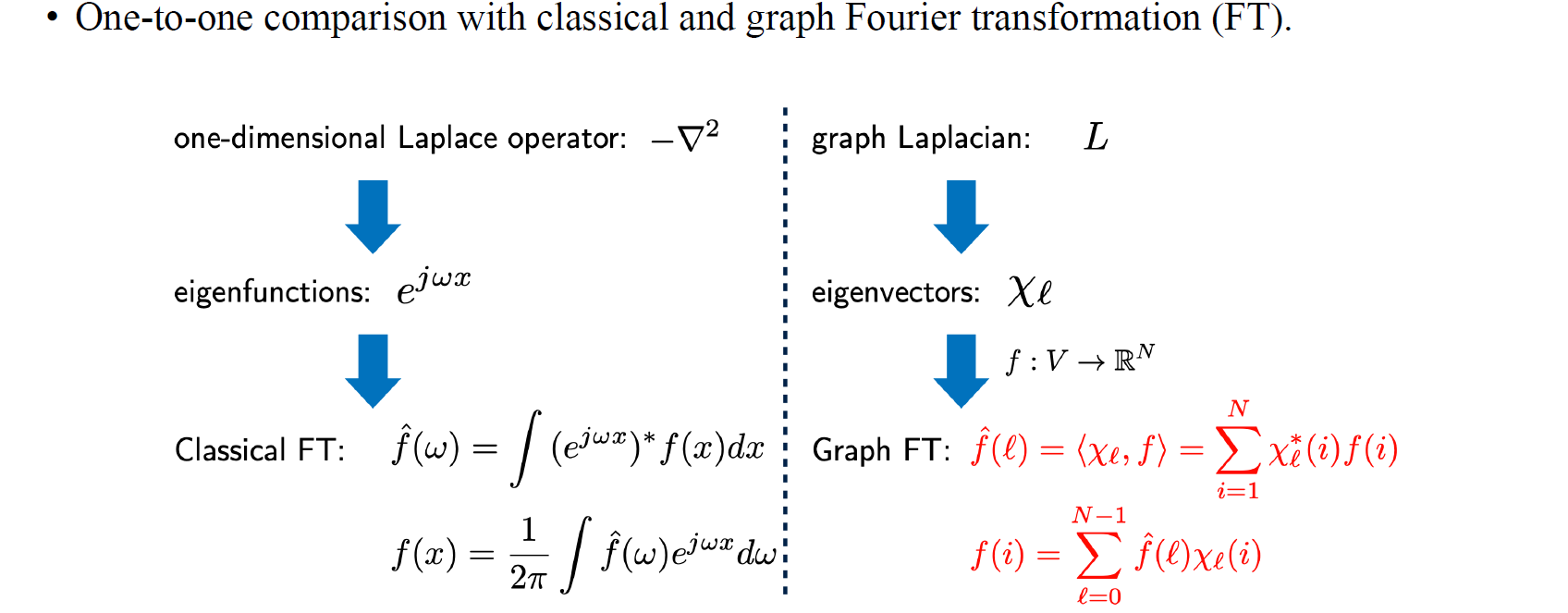Continuous한 경우에서 Fourier transformation와 graph Fourier transformation은 흥미로운 연관성이 존재한다. Continuous한 경우에는 Laplace operator가 존재하는 반면에 graph Fourier transformation에는 graph Laplacian $L$이 존재한다. Eigenfunction의 경우 $e^{j\omega x}$로 정의가 되며, 여기서 $\omega$는 $2\pi nk$로 정의될 수 있고, eigenvector의 경우에는 graph Laplacian matrix를 eigen decomposition을 통해서 얻을 수가 있다. Eigenvector의 경우 graph에 따라서 다르게 존재할 것이다. 아무래도 graph가 다르면 서로 다른 graph Laplacian이 존재하기 마련이다. 원래의 Fourier transformation이 좌측과 같이 구해진다면, graph Fourier transformation은 signal에 eigenvector를 곱해주면 된다.

간단한 예시를 보도록 하자. 위와 같은 graph가 주어졌다고 가정했을 때, orthogonal Laplacian eigenvector를 위와 같이 구성해서 discrete Fourier transform matrix를 만들 수 있을 것이다.

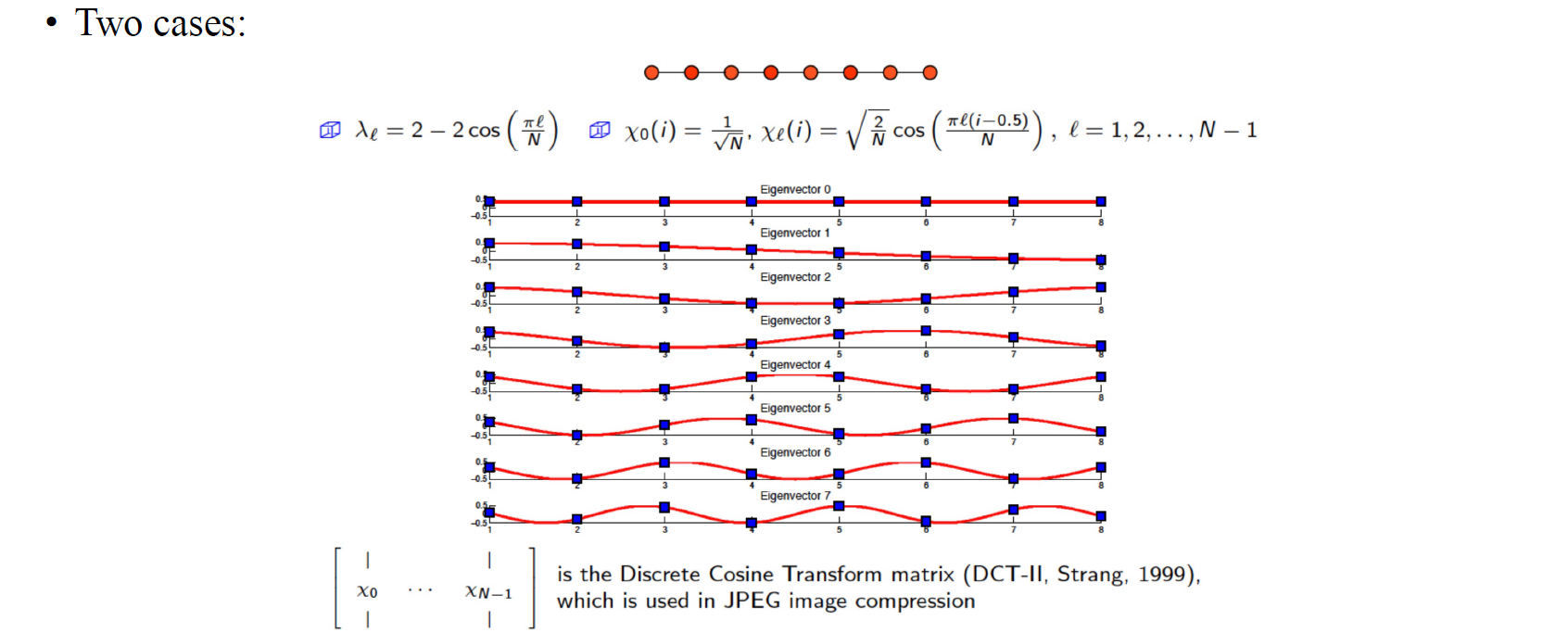Non-cyclic line graph에 대해서도 eigenvector를 위와 같이 구성하여 matrix $U$를 만들 수 있을 것이고, 우리는 이를 discrete cosine transform matrix라고 한다.

지금까지 우리는 graph Fourier transformation에 대해서 알아보았다. 이는 matrix $U$를 signal $x$에 곱해줌으로써 수행할 수 있고, $U$는 graph Laplacian을 eigen decomposition을 하여 얻어진 eigenvector들로 구성할 수 있다.

Filtering

Fourier transformation까지 알아봤으면 이제는 이를 기반으로 filtering을 할 수가 있다. Filtering의 경우 signal processing에서 가장 기본이 되는 개념 중 하나이다. Filtering operation의 주된 목적은 특정 frequency를 찾아내는 것이다. Filtering의 대표적인 예시 중 하나는 signal을 smooth하게 만드는 것이다. 왜냐하면 signal을 smooth하게 한다는 것은 높은 frequency component를 제거하는 것과 동일하기 때문이다. Signal $f$에 Fourier transformation을 하게 되면 coefficient set을 얻게 된다. Filtering을 하는 것은 frequency domain에서 특정 filter를 곱해주는 것과 같다. $\hat h(k)$에서 $k$가 높은 경우에는 이 값을 0으로 만들면 high frequency component를 없앨 수 있을 것이다. 반대로 $k$가 낮은 경우에는 이 값을 1로 설정해서 low frequency component들을 살림으로써 결국에는 signal을 smooth하게 만들 수가 있다. 이를 matrix 형태로 구해보면 Fourier coefficient $\hat f$에 filter $\hat h$를 element-wise product를 통해서 구해줄 수 있게 된다. 여기서 $\hat h$는 diagonal matrix로 생각하고 matrix multiplication을 $\hat f$와 하면 된다.

Convolution and Convolution Theorem

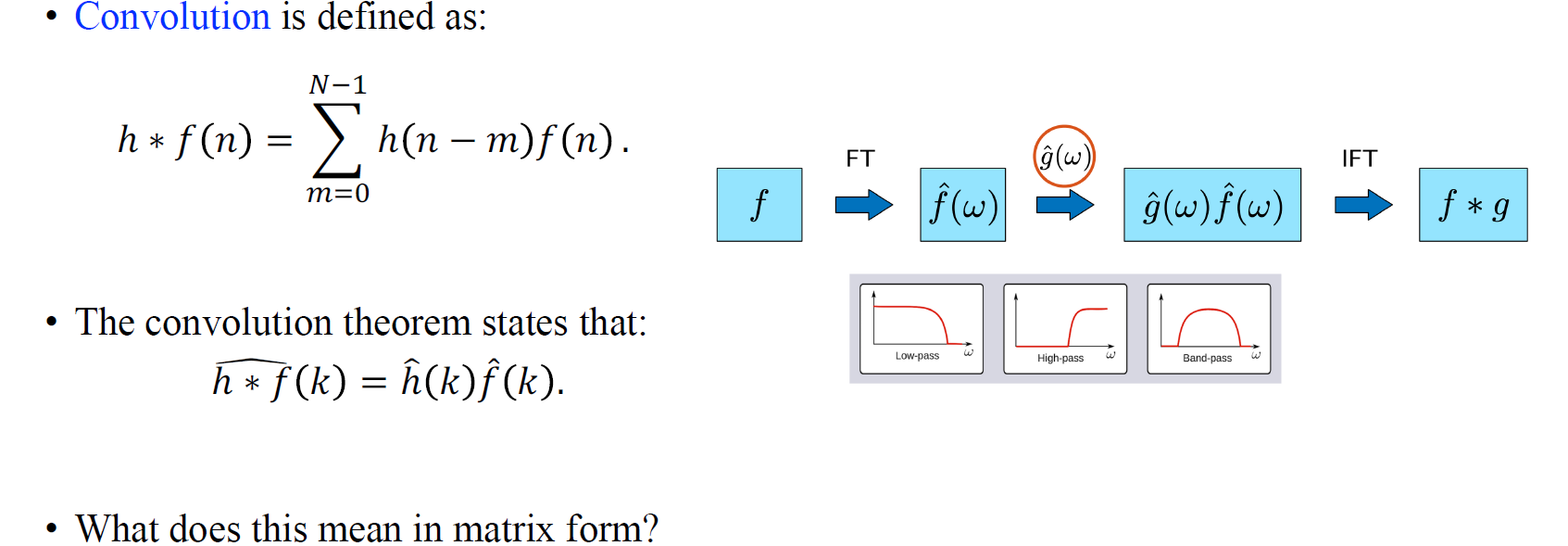우리는 이러한 filtering 과정을 또한 convolution으로 해석할 수 있다. Convolution이 정확히 어떠한 수식으로 구성되는지 보다는 여기서는 convolution이 frequency space 상에서 element-wise product로 수행되는 점이 더 중요하다. 그리고 우리는 convolution을 matrix의 형태로 표현하기를 원한다.

가장 먼저 function $f$를 Fourier transformation을 통해서 frequency space로 보낸다. 이는 eigenvector를 모아놓은 matrix $U^T$를 곱하면 된다. 그리고 element-wise product를 통해서 filter를 적용시킬 수 있다. 그리고 마지막으로 inverse Fourier transformation을 수행해준다. 이는 다시 matrix $U$를 곱해주면 된다.

Convolution theorem에서 convolution은 frequency space 상에서 element-wise product에 의해 유도된다. Convolution theorem은 두 signal 사이의 convolution을 이야기하는데, 이는 실제로 frequency space에서 element-wise product에 의해 수행이 된 다음에 inverse Fourier trnasformation을 적용하여 원래의 space로 돌아오게 된다. 이러한 과정은 matrix $U^T$를 곱하고 frequency-wise multiplication을 한 후에 inverse 변환을 위해 다시 $U$를 곱하는 과정과 동일하다.

이제 우리는 이로부터 graph convolution을 정의할 수 있게 된다. Graph convolution은 matrix $C$를 곱해주면 되는데, 여기서 $C$는 $U\text{Diag}(\hat h)U^T$로 parametrization 된 것을 볼 수 있다. 그리고 이 $C$는 graph Laplacian $L$과 eigenvector를 공유하게 된다.

Deriving 1D Convolution from First Principles

지금부터 adjacency matrix $A$로부터 eigenvector $U$를 사용하여 정의되는 alternative convolution에 대해서 알아보고자 한다. 지금까지 Laplacian matrix $L$을 가지고 graph convolution을 정의했다면, 이번에는 $A$를 가지고 정의할 것이다. Convolution을 matrix로 정의하여 $Cf$ 형태는 동일하지만 $C$를 구성하는 $U$는 $A$를 eigen decomposition을 통해서 얻어진 eigenvector들로 구성이 되어져 있다. 1D time series graph의 경우에는 $A$와 $L$의 eigenvector가 동일할 것이다. 이는 여기서는 중요한 내용은 아니며, 흥미로운 점은 $C$와 $A$가 invertible하다는 것이다. 그래서 $CA$와 $AC$가 동일한 결과를 만들어낼 수 있다. 이전에 1D signal에 관한 matrix multiplication은 time-shift operator와 같다고 했다. 그래서 1D convolution의 경우 shift-equivariance 성질을 만족하게 된다. Convolution을 먼저하고 signal을 shifting하는 것과 signal을 shifting하고 convolution을 수행하는 것이 결과적으로는 동일한 행위인 것이다. 이러한 점으로부터 중요하고 흥미로운 성질이 생기고, 이는 convolution이라는 것이 shift-equivariant한 operator이기 때문이다. 실제로 어떠한 shift-equivariant한 matrix multiplication도 convolution이 될 수 있다.

Time-shift operator와 순서를 바꿀 수 있는 matrix를 우리는 circulant matrix라고 하며, 이는 위와같이 각 column에서 순서가 하나씩 이동되는 row들의 집합이다. 이는 matrix multiplication과 같은 linear operator가 shift-equivariant하다면, 이는 곧 convolution임을 의미하게 된다.

ChebNet and GCN

이제 마지막으로 GCN이라 불리는 graph convolution network가 어떻게 정의되었는지에 대해서 알아보고자 한다. 실제로 GCN 논문을 보게되면 이번에 알아본 graph convolution의 정의를 기반으로 설명되어져 있다. 여기서 graph convolution은 단지 adjacency matrix를 곱하는 것이 전부가 아니라, frequency filtering process를 수행하는 것과 같다고 한다.

ChebNet과 GCN은 2016년도에 동시에 등장했으며, 서로를 언급하지 않은 상태로 논문이 작성되었다. 근본적으로 이들은 동일한 방법론을 제시하였다. GCN은 우리가 convolution matrix를 $U\text{diag}(\theta)U^T$로 어떠한 matrix로도 정의할 수 있기 때문에 graph convolution 과정을 diagonal matrix의 $\theta$로 parameterization할 수 있다고 이야기한다. 각 diagonal에 parameter를 할당하여 graph convolution을 하면 된다고 하고, 이는 각 filter를 조절하는 것과 동일하게 볼 수 있다. $\theta_1$은 $\lambda_1$에 해당하는 signal을 조절하는 식이다.

Signal이 있을 때 $U$를 곱하고 다시 filter를 곱하고 다시 $U$를 곱하는 이러한 과정이 비효율적으로 여겨진다. 무엇보다도 adjacency matrix를 eigen decomposition을 하는 과정부터 사실 cost가 많이 든다고 볼 수 있다. 그리고 parameter의 숫자가 vertex의 수의 비례해서 증가하는 부분도 문제가 될 수 있으며, 그래프가 변하게 되면 우리는 새로운 parameter를 할당해야하는 번거로움도 존재한다. 즉, 모든 graph에 일반적으로 접근할 수 없다는 것이다. 어찌됐든 graph가 커지기만 하더라도 이러한 식의 parameterization은 비효율적이게 된다.

ChebNet은 결국 이러한 비효율적인 과정을 Chebyshev polynomial을 사용해서 근사할 수 있음을 보여주었다. 이는 polynomial을 여러번 더하게 되면 임의의 function으로 근사시킬 수 있게 된다. 그리고 이는 polynomial이 여러번 더해지면서 coefficient가 $\theta_k$로 parameterization 되었음을 위의 식을 통해서 볼 수 있다. GCN은 first-order Chebyshev polynomial만으로도 동일하게 동작할 수 있음을 설명하였다. 그리고 이를 수식으로 정리해보면 그저 adjacency matrix를 곱하는 것과 동일함을 알 수 있다. 즉, first-order Chebyshev polynomial을 사용하는 것이 adjacency matrix를 곱하는 것과 동일하다는 것이다. GCN이 이름에서 보았듯이 graph convolution network일지라도 graph convolution을 first-order Chebyshev polynomial로 근사한 것임을 알아두자.