Overview
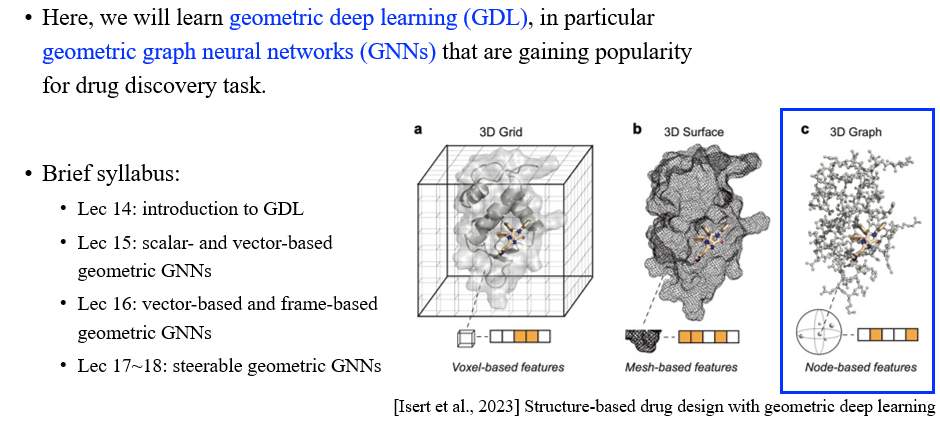Graph neural network (GNN)을 공부하다가 보면 한번쯤은 GNN이 geometric deep learning의 일부분이라는 것을 들어볼 수 있고, GNN에 대해서 이미 친숙하다면 geometric deep learning (GDL)에 대해서 어렵지 않게 이해할 수 있을 것이다. GNN에 대해서 어느정도 알았다면 순차적으로 다음에는 GDL이라는 거대한 파트에 대해서 알아볼 차례이다. 특히, geometric GNN에 대해서 이번에 알아볼 것이다. Geometric GNN은 3D graph에 대해서 정의되는 GNN으로, 이에 대해서는 다음에 조금 더 자세하게 알아볼 것이고, 이번에는 GDL에 대해서 간단하게 이해해보고자 한다. GDL은 3D grid 구조에 대해서 관련이 있으며, 여기에는 3D voxel, surface, graph 등이 포함될 수 있다.
What is Geometric Deep Learning?
GDL이란 무엇일까? Geometric이라는 단어를 사람들에게 물어보았을 때 원이나 삼각형 등의 도형과 관련지어 대답할 수도 있고, Euclidean 공간과 같은 개념을 언급할 수도 있을 것이다. 모두 틀린 대답은 아니지만 우리가 여기서 이야기하고자 하는 GDL에서의 geometric은 조금 다를 수가 있고, 우리는 이에 대해서 알아보고자 할 것이다.
Machine learning은 black-box function을 어떻게 골라야하는지에 대한 방법으로, GDL은 또한 이러한 질문에 대한 답변이 될 수도 있다. 예를 들어, 위와 같이 이미지가 주어졌을 때 cat, dog와 같이 이미지에 특정 단어를 mapping시켜야 한다고 해보자. 여기서 model 는 주어진 이미지에 대해 cat과 dog를 binary label로 mapping 시켜주는 역할을 할 것이다.
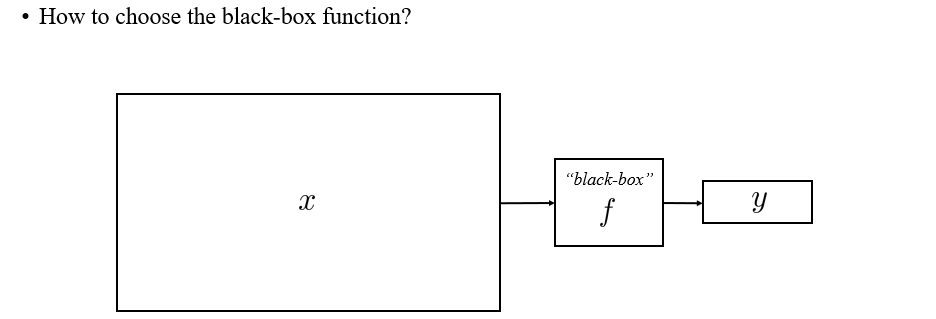결국 model 의 입장에서는 단순히 input 가 들어오면 output 로 mapping시켜주기만 하면 된다. 그리고 여기서 deep neural network (DNN)은 model의 역할을 할 수 있는 하나의 선택지가 되는 것이다.
Deep Neural Networks (DNNs)
DNN을 통해서 우리가 제안하는 어떠한 machine learning algorithm을 설명할 수 있는 를 선택할 수 있는 것이다.
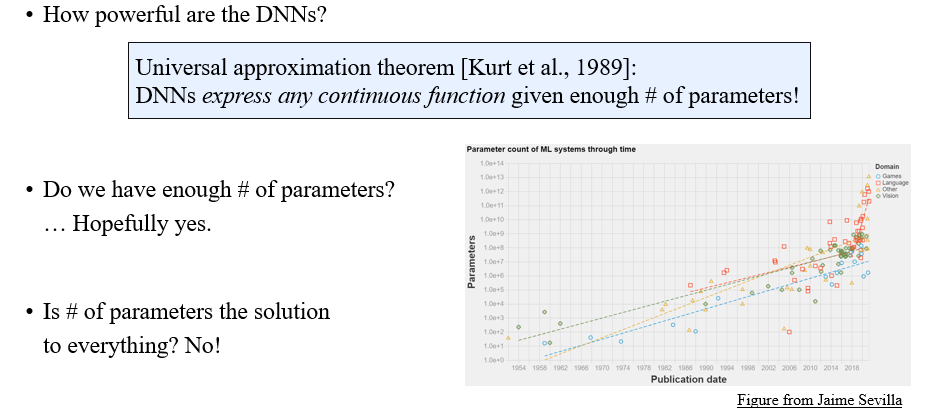우리는 DNN이 정말로 강력하다는 사실을 알고 있다. 충분히 많은 parameter가 주어진다면 2-layer의 DNN으로 어떠한 continuous function을 표현할 수 있다는 universal approximation theorem을 통해서도 DNN의 강력함을 설명할 수 있다. Expressive power의 관점에서 충분히 많은 parameter를 통해 DNN은 어떠한 function도 표현이 가능하기 때문에 좋은 선택지가 되는 것은 맞지만, GDL은 모든 상황에서 이러한 expressive power가 해결책이 된다고 이야기하지는 않는다.
The Problem of Overfitting
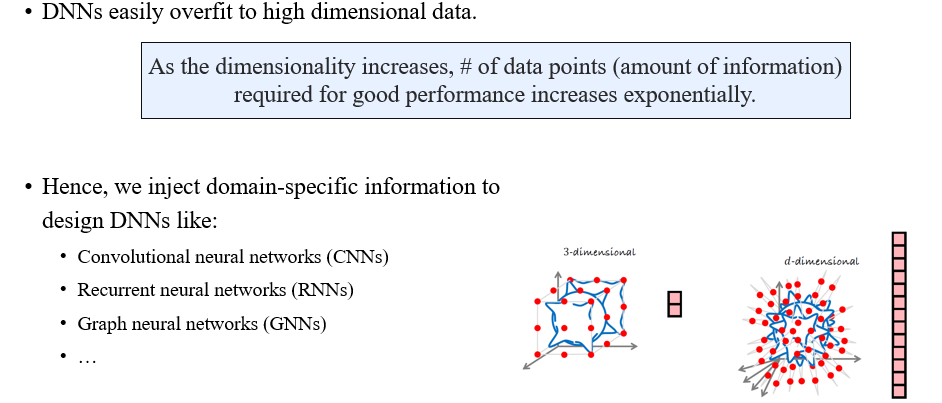이러한 점은 바로 overfitting과 관련이 있다. DNN이 정말로 표현하는 측면에서는 강력한 수단이지만, 고차원의 data에 있어서는 쉽게 overfitting되는 문제가 존재한다. Data의 차원이 올라갈수록 더 좋은 성능을 얻기 위해 필요한 data의 수가 기하급수적으로 많이 요구되어진다. 이는 data의 개수와 overfitting 사이에서의 trade-off 관계가 된다. Parameter의 수가 많아지게 되면 그만큼의 data 수도 추가로 요구되어지는게 사실이다. 그래서 사람들은 이러한 문제를 해결하기 위해서 모델에 domain knowledge를 추가하려는 시도를 하곤한다. 이러한 domain-specific information을 이용해서 DNN을 설계한 결과가 CNN, RNN, GNN 등의 모델들이다.
Zoo of DNN Architectures
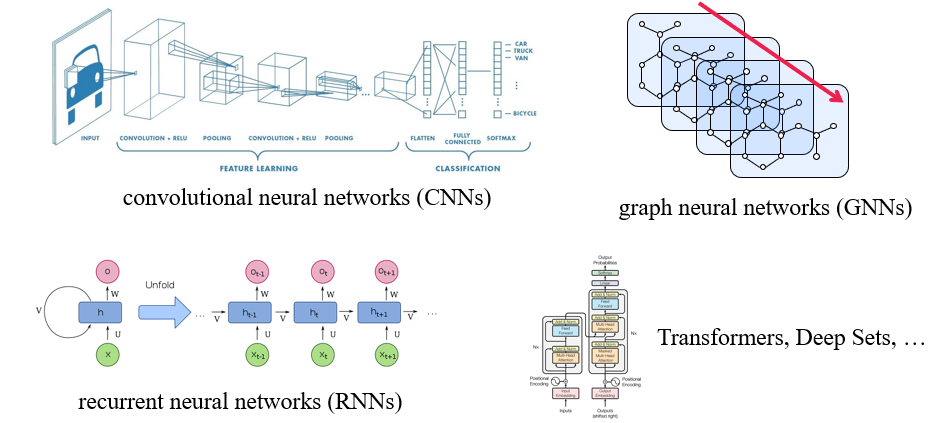GDL은 결국 이러한 부분과 관련이 있는 것으로, GDL은 우리가 특정 상황에 맞게 domain-specific information을 모델에 주입시켜야함을 이야기한다. DNN의 구조가 특정 domain에 맞게 설계가 되어오고 있으며, 위와 같이 image에는 CNN이 어울리고 text에는 RNN이 어울리는 식으로 발전해오고 있다. 우리가 주목하고 있는 GNN의 경우에는 graph domain에 특화되었다고 이야기할 수 있다.
결국 DNN을 설계하는데 있어서 주어진 dataset에서의 characteristic이 상당히 중요한 부분으로 작용하는 것이다. 어떠한 dataset이 들어오는지에 따라 DNN의 구조를 바꿀 수 있는 것이 어떻게 보면 가장 신경써야하는 부분인 것이다. 이러한 생각이 결국 GDL의 아이디어로 연결이 된 것이다.
구체적으로 GDL이 말하고자 하는 것은 이러한 dataset의 characteristic이 우리가 geometry라고 부르는 것으로 설명될 수 있다는 것이다. Dataset의 서로 다른 geometry가 주어졌을 때, 어떻게 이러한 geometry를 DNN 구조에 통합시킬 수 있는지가 우리에게 주어진 과제인 것이다.
Why is a Geometry?
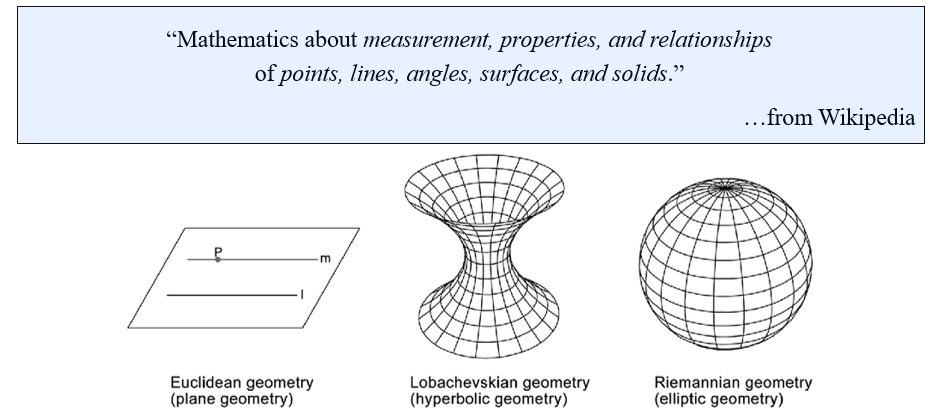그렇다면 geometry라는 것은 구체적으로 어떠한 것을 말하는 것일까? Geometry는 여러가지로 정의가 될 수 있다. 형식적인 정의로 wikipedia에서의 geometry 정의는 "Mathmatics about measurement, properties, and relationships of points, lines, angles, surfaces, and solid."이다. 이러한 정의가 어떻게 보면 가장 informal한 정의일 수 있다. 그리고 geometry가 Euclidean geometry, hyperbolic geometry, elliptic geometry 등으로 구분될 수 있다고 하는데, 이는 어떻게보면 우리 입장에서는 조금 어울리지 않다고 생각될 수 있다. 이러한 개념들을 정의할 때는 일반적으로 역사적인 배경을 가지고 있기 때문이다. 수백년 전에 정의가 되는 이러한 개념들의 문제는 컴퓨터 공학이나 AI를 전공하는 사람들 입장에서는 그러한 의미보다는 실제로 적용하고 활용하기 위해서 이들을 refactoring이나 organizing을 거쳐 geometry를 통해 우리가 실제로 전달하고자 하는 바를 이야기해야 하기 때문이다.
Geometry
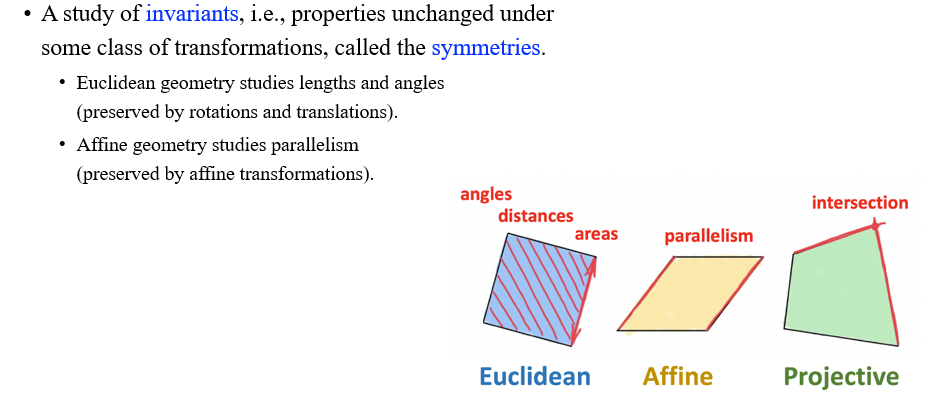그래서 시간이 흘러 사람들이 생각을 모아 합의점에 도달한 내용이 geometry를 invariance로 이야기하고자 하는 것이다. 따라서 geometry는 특정 object의 고유한 특성과 관련된 학문이 되었고, 이러한 특성은 symmetry라고 하는 어떠한 transformation 하에서도 변하지 않는 성질을 설명하게 되었다. 어떻게 보면 이러한 것들이 철학적인 질문으로 여겨질 수 있다. 이러한 성질이 의미하는 것은 무엇이며, 여기서 transformation이 의미하는 것은 또한 무엇인지 생각해볼 수 있기 때문이다.
예를 들어, Euclidean geometry는 rotation과 translation에 invariant한 geometry이다. 이러한 transformation을 우리는 Euclidean transformation이라 부를 수 있다. 결국 Euclidean geometry는 Euclidean transformation과 관련이 있다는 것이고, 여기서 object가 rotation과 translation에 invariant하다는 것은 length와 angle에 직접적인 관련이 있기에 Euclidean geometry는 결국 length와 angle에 대해서 연구하는 것으로 정리될 수 있다. Affine geometry는 parallelism과 관련이 있으며, 이는 affine transformation에 invariant함을 설명하게 된다.
Geometry of Data
이러한 내용들을 보면 결국 geometry라는 것은 object의 identity에 관해서 연구하는 것으로 생각해볼 수 있다. 어떠한 transformation에도 변하지 않는 object의 성질이 있고 이를 identity라고 정의할 수 있으면 이를 우리는 invaraince로도 생각할 수 있는 것이다. 여기서 identity를 바꾸지 않는 transformation을 우리는 symmetry라고 부르게 된다. 예를 들어 원이나 삼각형과 같은 것은 rotation을 통해서 원래의 identity를 바꿀 수 없기 때문에 이들을 symmetry로 정의할 수 있는 것이다.
그렇다면 data의 geometry는 무엇일까? 매우 유명한 예시로 data augmentation이 있다. 우리가 data의 geometry를 이야기할 때마다 transformation에 대해서 변하지 않는 data의 identity에 대해서 말할 필요가 있다. 기본적으로 이러한 transformation은 항상 image classification 등에 대해서 이야기할 때 등장하곤 한다. 우리가 cat이라는 image가 주어졌을 때, 이를 이동시키거나 회전시키거나 아니면 크기를 바꾸더라도 identity가 바뀌는 것이 아니기 때문에 classification의 결과가 바뀌어서는 안되는 것이다.
Geometric Deep Learning
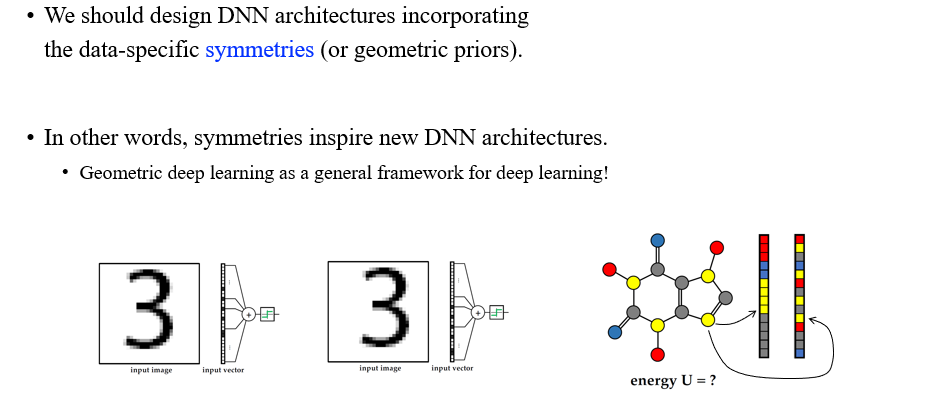GDL은 data 특유의 symmetry를 통합하여 deep neural network를 설계하는데 필요한 아이디어이다. 그리고 이를 우리는 geometri prior라고 부를 것이다. CNN은 대표적인 GDL의 구조로, image가 가지고 있는 translation symmetry를 고려하였다.
Examples of Geometric Priors
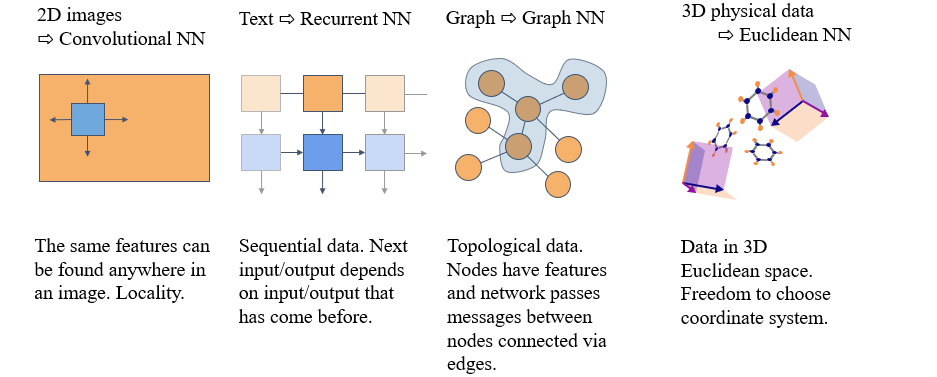이러한 식으로 GDL을 이용하여 다양한 framework가 등장하게 되었다. 예를 들어, 2D image에서의 symmetry를 이용하여 설계된 것이 CNN이고, text에서의 translation symmetry를 이용하여 설계된 것이 RNN이며, graph에서의 symmetry를 이용하여 설계된 것이 GNN이다. 이렇게 대표적인 3개의 neural network 외에도 3D physical data에 맞게 설계된 Euclidean neural network가 존재한다. 이러한 3D data는 3D Euclidean space에서 정의가 되며, 기존의 다른 data와는 다르게 조금 더 섬세하게 정의가 되는 부분이 존재한다.
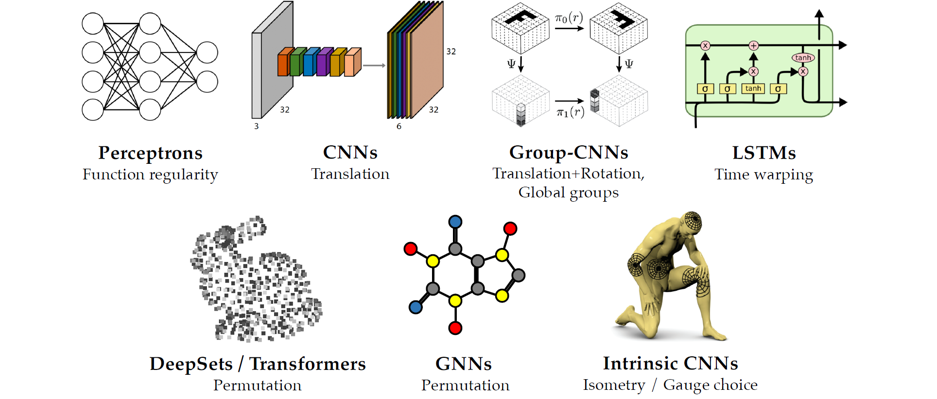GDL은 매우 큰 framework이며, 이는 deep learning의 핵심으로 생각해볼 수 있다. 왜냐하면 우리가 어떻게하면 자동적으로 deep learing이라는 것을 얻을 수 있는지 말하고 있으며, 지금까지도 어떻게 deep learning framework를 설계해야하는지를 알려주고 있기 때문이다. 위의 예시들은 대표적인 geometric prior들로 어떠한 invariance가 요구되어지는지를 간략하게 이야기하고 있다. 여기까지가 간단하게 GDL이 무엇인지에 대해서 알아보았다.
