
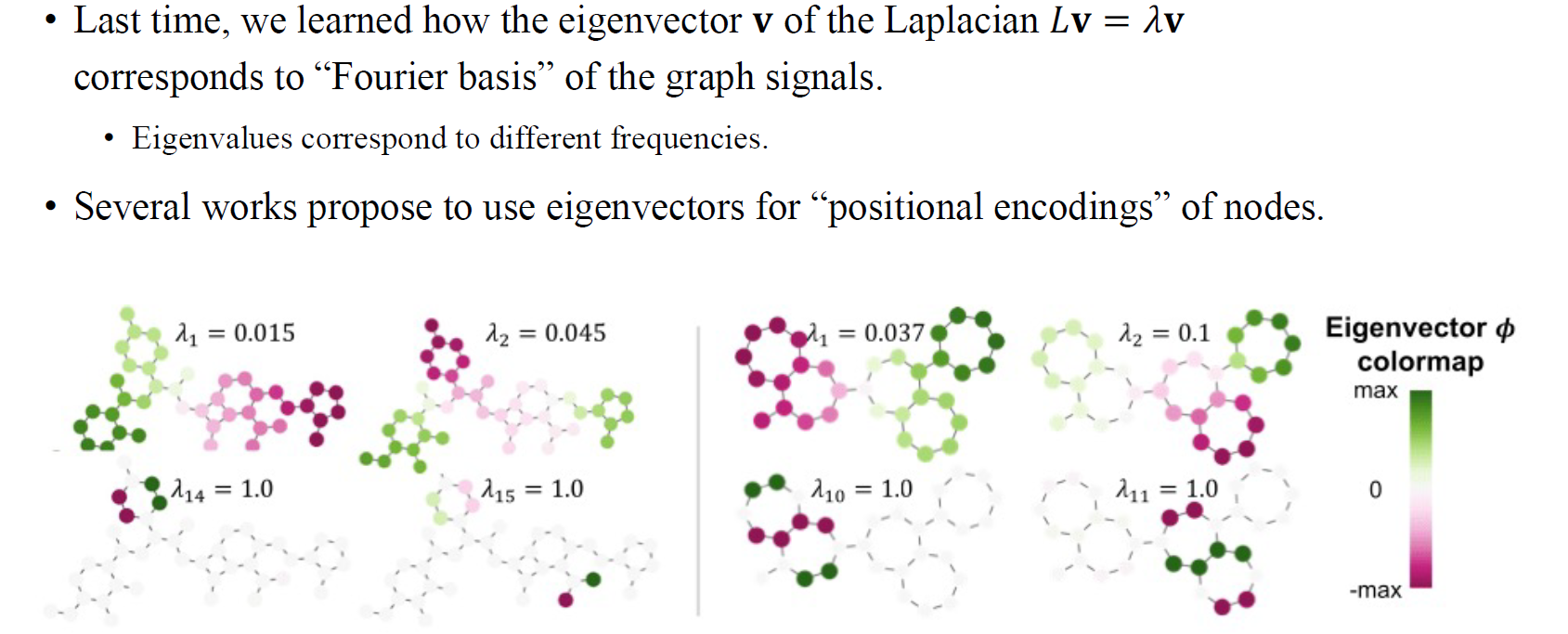
 이번에는 GNN과 관련하여 Laplacian positional encoding에 대해서 알아볼 것이다. 이 내용은 사실 transformer에 이미 등장했던 개념으로 다시 한번 이 부분에 대해서 자세하게 알아보고자 한다. 먼저 Laplacian matrix 로부터 시작할 것이다. 은 degree matrix에서 adjacency matrix를 빼주면 쉽게 얻을 수 있다. 의 eigenvector 는 graph signal processing에서 Fourier basis에 해당하고, eigenvalue 는 서로 다른 frequency를 나타낸다. 만약 eigenvalue 가 매우 작으면 eigenvector가 smooth하다는 것을 의미하게 된다. 반대로 eigenvalue 가 매우 크면 이웃한 vertex들끼리 서로 다른 값을 지니게 되어 서로 다른 색을 가지는 것을 볼 수 있다. 이는 graph signal이 매우 격하게 파동하는 것을 의미한다. 사람들은 이러한 내용을 기반으로 time series data에 Fourier basis들을 positional encoding으로 사용해오고 있다. 그래서 우리는 graph signal에 Laplacian positional encoding을 사용하고 싶다는 것이다.
이번에는 GNN과 관련하여 Laplacian positional encoding에 대해서 알아볼 것이다. 이 내용은 사실 transformer에 이미 등장했던 개념으로 다시 한번 이 부분에 대해서 자세하게 알아보고자 한다. 먼저 Laplacian matrix 로부터 시작할 것이다. 은 degree matrix에서 adjacency matrix를 빼주면 쉽게 얻을 수 있다. 의 eigenvector 는 graph signal processing에서 Fourier basis에 해당하고, eigenvalue 는 서로 다른 frequency를 나타낸다. 만약 eigenvalue 가 매우 작으면 eigenvector가 smooth하다는 것을 의미하게 된다. 반대로 eigenvalue 가 매우 크면 이웃한 vertex들끼리 서로 다른 값을 지니게 되어 서로 다른 색을 가지는 것을 볼 수 있다. 이는 graph signal이 매우 격하게 파동하는 것을 의미한다. 사람들은 이러한 내용을 기반으로 time series data에 Fourier basis들을 positional encoding으로 사용해오고 있다. 그래서 우리는 graph signal에 Laplacian positional encoding을 사용하고 싶다는 것이다.
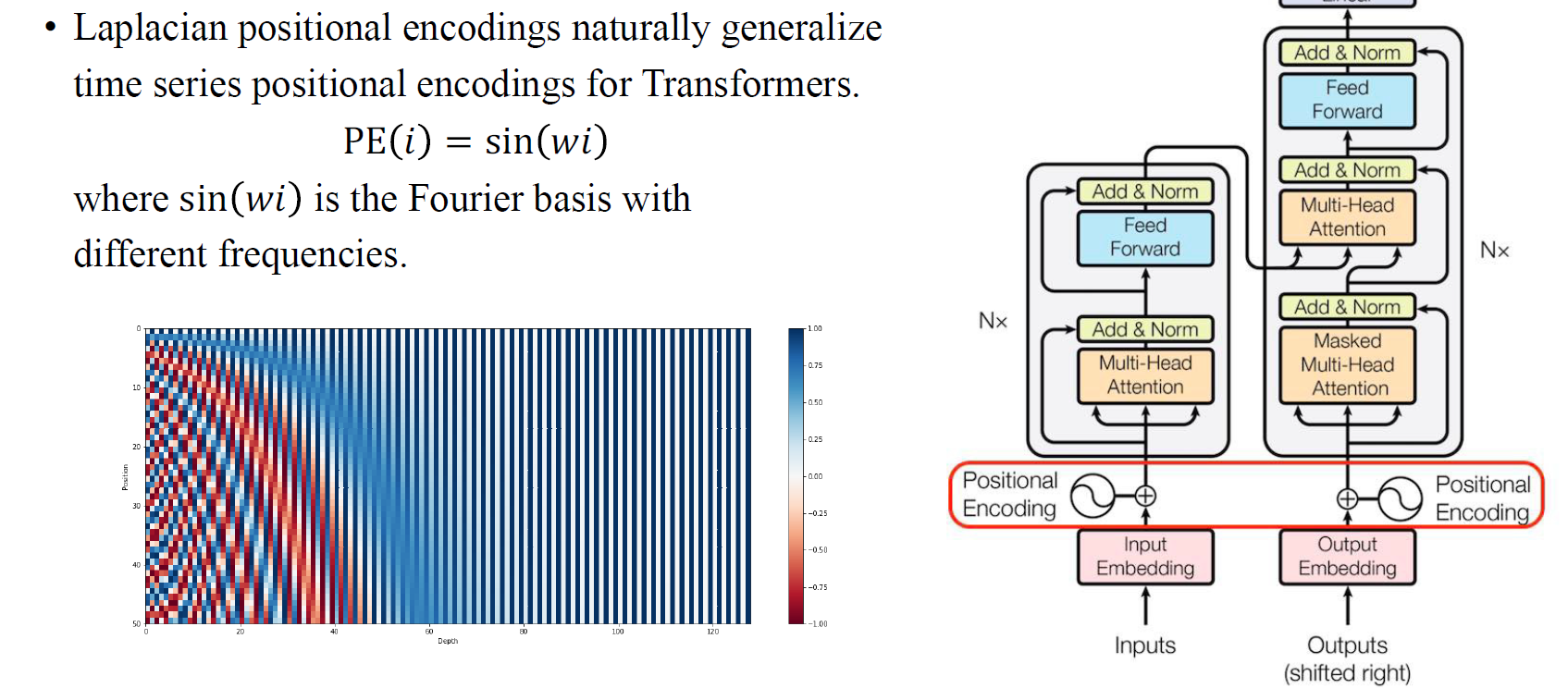 이러한 부분은 transformer에서 주로 사용되었는데, transformer가 각 vertex의 position을 파악할 수 없기 때문이다. Input embedding에 positional encoding 정보를 추가해줘서 transformer가 input vertex들의 position을 파악하도록 하는 것이다. 위의 식에서 에 따라 서로 다른 frequency를 가지는 Fourier basis 를 선택할 수 있는 것이다. 좌측 아래는 positional encoding이 어떻게 이루어지는지 visualization한 결과이다.
이러한 부분은 transformer에서 주로 사용되었는데, transformer가 각 vertex의 position을 파악할 수 없기 때문이다. Input embedding에 positional encoding 정보를 추가해줘서 transformer가 input vertex들의 position을 파악하도록 하는 것이다. 위의 식에서 에 따라 서로 다른 frequency를 가지는 Fourier basis 를 선택할 수 있는 것이다. 좌측 아래는 positional encoding이 어떻게 이루어지는지 visualization한 결과이다.
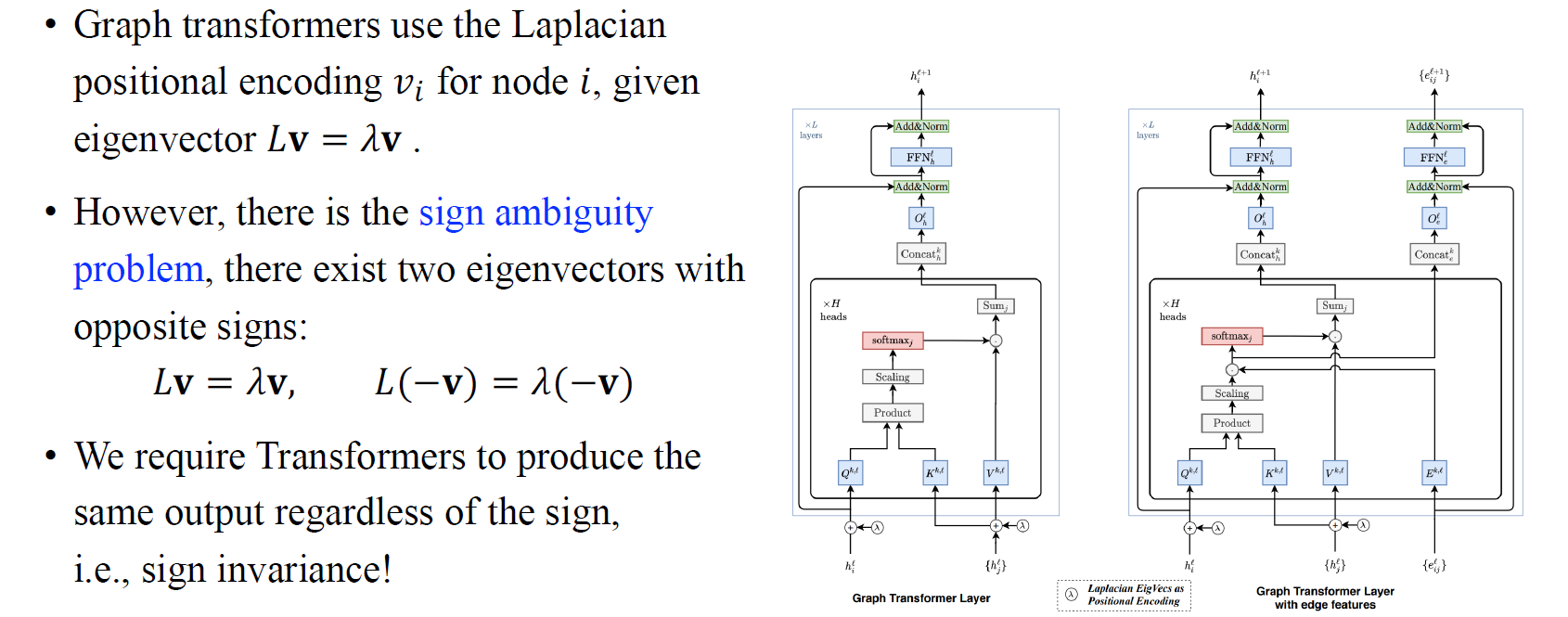 Laplacian eigenvector가 graph signal에서의 Fourier basis라는 사실로부터 graph transformer는 node 에 대해서 Laplacian positional encoding 를 사용해왔다. 이러한 방식이 graph data에 대해서 transformer를 일반화할 수 있도록 하였다.
Laplacian eigenvector가 graph signal에서의 Fourier basis라는 사실로부터 graph transformer는 node 에 대해서 Laplacian positional encoding 를 사용해왔다. 이러한 방식이 graph data에 대해서 transformer를 일반화할 수 있도록 하였다.
하지만, 이렇게 Laplacian positional encoding을 사용했을 때 한가지 문제점이 존재한다. 바로 sign ambiguity problem이다. Eigenvector 와 에 대해서 동일한 eigenvalue가 존재하게 된다. 하지만 eigenvector의 부호가 다르기 때문에 두 종류의 representation이 존재하는 것이다. 두 vector에 따라 서로 다른 output으로 연결이 되는데, 비록 동일한 position을 가지고 있더라도 GNN의 output은 각 vector에 따라 다르게 정의되어야 한다. 하지만 우리가 원하는 것은 부호와 관련없이 동일한 output을 얻고싶은 것이다. 즉, eigenvector로부터 sign invariance를 가지기를 원한다.
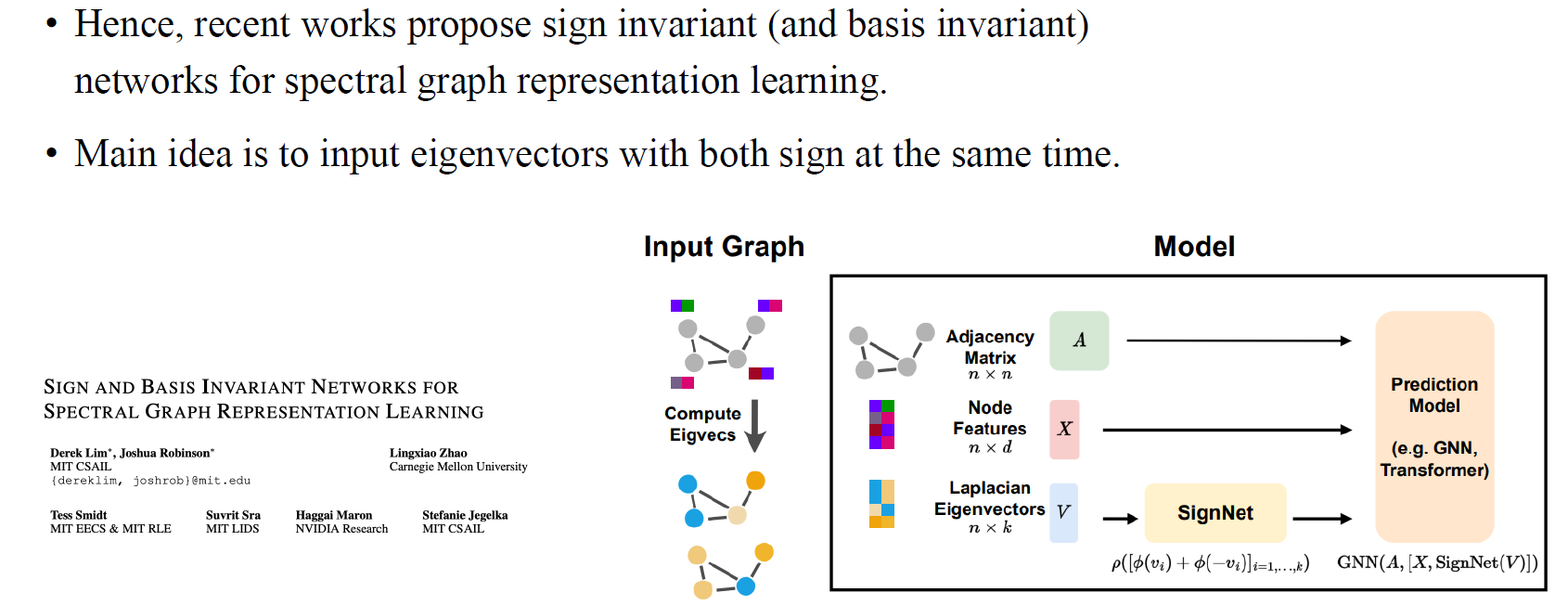 Graph transformer가 나온 이후로 사람들은 sign invaraince를 가지는 network를 연구하기 시작했고, 2022년도에 sign invariant network가 등장하게 된 것이다. 단순히 하나의 eigenvector를 input으로 넣어주는 것이 아니라 서로 다른 부호를 가지는 2개의 eigenvector를 input으로 넣어주는 것이 이들의 아이디어였다. Permutation invariant한 방식으로 2개의 eigenvector를 network 내에서 처리하도록 하였다. 이렇게 간단한 아이디어로도 sign invariance를 만족시킬 수가 있었다.
Graph transformer가 나온 이후로 사람들은 sign invaraince를 가지는 network를 연구하기 시작했고, 2022년도에 sign invariant network가 등장하게 된 것이다. 단순히 하나의 eigenvector를 input으로 넣어주는 것이 아니라 서로 다른 부호를 가지는 2개의 eigenvector를 input으로 넣어주는 것이 이들의 아이디어였다. Permutation invariant한 방식으로 2개의 eigenvector를 network 내에서 처리하도록 하였다. 이렇게 간단한 아이디어로도 sign invariance를 만족시킬 수가 있었다.
