[그래프 기계학습] Graph Signal Processing 4

Wavelet Transform on Graphs

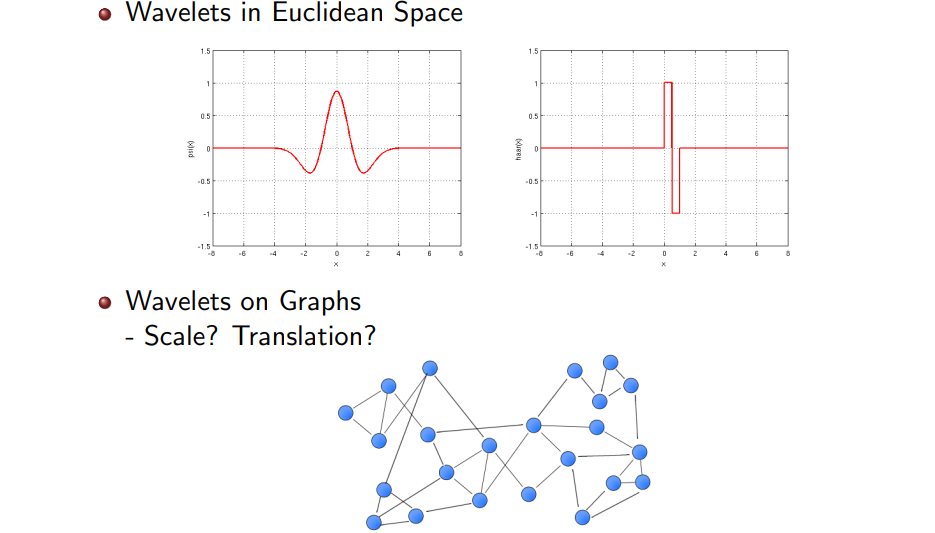Wavelet transformation (WT)에 대해서 알아보았으면, 이제부터는 본격적으로 WT를 graph에 어떻게 적용하는지 알아보자. 결국 signal processing을 graph에 대해서 수행하는지 알아보고자 한다. Graph는 위와 같이 여러개의 node로 구성되어 있으며, 이 node들이 임의의 edge를 통해서 다른 node들과 연결되어 있다. 이러한 domain이 주어졌을 때 signal이라는 것을 어떻게 정의할 수 있을까? 결국 WT을 하기 위해서는 transformation에 사용되는 basis를 설계할 필요가 있다. 그래서 graph를 signal로 이해하고 transformation을 적용하기 위해서는 가장 먼저 basis를 설계하고 이후에 transformation을 수행해야 한다. Basis는 우리가 하고자 하는 특정 task에 따라 서로 다르게 설계할 수 있다. 어떠한 task를 하든간에 basis를 미리 정의하는 일은 필수적이다.

그러나 우리가 실제로 다뤄야하는 signal은 time space나 image space와 같은 Euclidean space이다. 이는 곧 지금까지의 domain들은 전부 regular한 structure를 포함하고 있었다는 의미이다. 모든 것이 직선으로 설명이 가능했었다. 2차원의 image만 하더라도 $x$축과 $y$축을 기준으로 설명할 수가 있었다. 우리가 이번에 사용하는 graph domain은 이러한 규칙적인 구조를 지니고 있지 않다. 기본적으로 graph의 node가 여기서는 특정 domain이 될 것이다. 이러한 구조에서 scale과 translation을 어떻게 정의할 수 있을까? 우리가 Haar wavelet을 정의해서 사용한다고 하더라도 어디가 center가 될 수 있는 것일까?

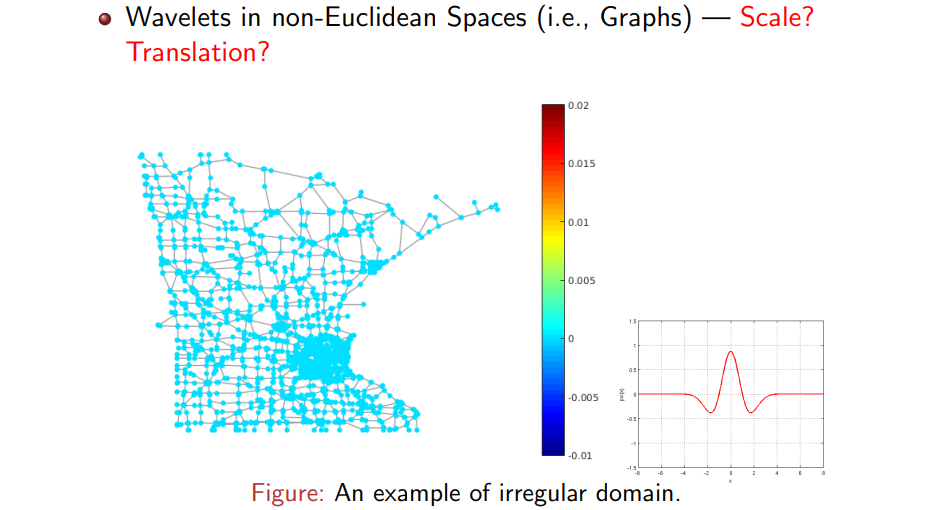결국 graph와 같이 non-Euclidean space에서 wavelet을 어떻게 정의하고, scale과 translation을 어떻게 정의할 수 있는지가 이번 내용의 핵심이라고 볼 수 있다. 위의 예시와 같이 어떠한 도시의 지도가 graph처럼 되어있다고 생각해보자. 각 node는 어떠한 대도시 속 작은 도시에 해당하고 이를 연결하는 길을 edge라고 생각하면 된다. 각 node는 결국 어떠한 signal을 가지고 있을 것이고, 우리는 Fourier transformation (FT)나 WT 등을 통해서 이러한 signal을 분석하기를 원한다. 가장 먼저 우리는 graph의 node에 대한 mother wavelet의 모양을 미리 정하고 정의해야 한다.

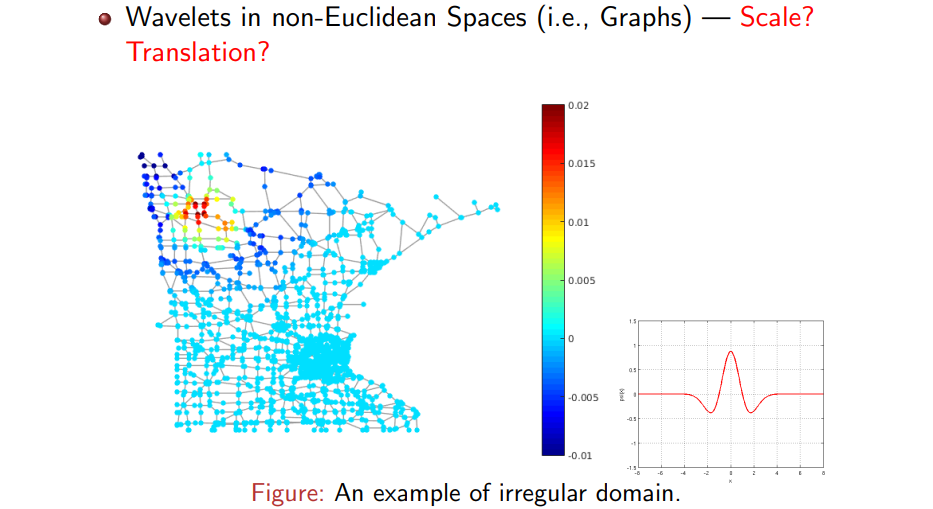Mother wavelet은 center 영역에서 증가하고 감소하는 부분이 있고 나머지는 0으로 수렴하는 것이 일반적인 형태이다. 여기서 scale을 증가시키게 되면 frequency 상에서 basis는 더 줄어들게 될 것이다. Wavelet의 특징 중 또 다른 하나는 어디든 이동시킬 수 있다는 것이다. 만약 이러한 basis function을 우선순위로 정의할 수 있다면, 즉, 만약 graph에서 shape을 정의할 수 있다면, 결국에는 WT를 정의할 수 있게 된다. 그러나 graph의 node에는 어떠한 regularity도 존재하지 않기 때문에 이는 현실적으로 불가능하다. 이렇게 graph의 shape을 몰라 미리 정의해야하는 wavelet을 정의하기 어렵기 때문에 정말 혼란스러운 상황이 된다. 물론 이렇게 할 수 있는 방법이 존재하기는 하다.

Vertex set $V$와 edge set $E$, 그리고 edge가 가지는 signal $\omega$를 통해 표현되는 $G$라는 domain이 주어졌다고 해보자. 여기서 $\omega$는 vertex를 연결하는 edge weight를 나타낸다. 이제 우리는 time도 image도 아닌 graph라는 domain을 다루고 있고, 특히 이는 vertex set $V$에 의해 정의된다. 앞서 이야기 했듯이 graph space에서 basis를 구성하는 일은 feasible하지 못하다. 우리가 하고자하는 것은 frequency space에서 filter를 구성하는 것이고, 이 filter의 inverse transformation을 통해서 원래 space로 돌아오고 싶은 것이다. 이렇게 되면 결국 우리가 원하던 WT을 성공하는 것이다. WT은 frequency space에서 적용할 수 있는 filter에 의해서 정의가 되어 inverse transformation까지 수행할 수 있어야 한다. 이는 continuous space에서 정의되는 WT이고, 이를 graph space에서까지 정의하고자 한다. 실질적으로 graph space를 직접 다루는 것보다 frequency space에서 filter를 설계하고 inversion을 하는 것이 graph에서 WT을 수행할 수 있는 방법이 된다. 여기서의 filter는 band-pass filter이고, 우리는 filter의 모양을 frequency space에서 설계할 수 있다.

Signal은 기본적으로 time space에서 정의된다. 그리고 이를 이용해 문제를 풀기 어렵기 때문에 또 다른 space인 frequency space로 보내서 문제를 해결하고자 하는 것이다. Frequency space에서 문제를 해결하는 것이 더 쉽기 때문에 여기서 문제를 해결하고 다시 원래의 space로 transformation시키면 되는 것이다. 이때 wavelet을 구성하는 것은 time space에서 하는 것이 아니다. 특히, graph space에서는 더욱 어려울 것이다. Wavelet $\psi$는 frequency space에서 만들어지는 것이 더 쉬운 일이다. 나중에 이를 inversion 시키면 되기 때문에 원하는대로 filter를 만들기 위해서는 frequency space에서 $\psi$를 만들면 된다. 결국, graph에서 문제를 풀기 어렵기 때문에 다른 space에서 이를 해결하고 다시 graph space로 돌아오고자 하는 것이고, 이를 위해 graph에서 WT을 하기 위한 핵심은 바로 freuqency space에서 wavelet을 어떻게 구성할지이다.

그렇다면 가장 먼저 어떻게 graph를 frequency space로 보낼 수 있을까? 기존의 signal을 Fourier transform (FT)를 통해서 보냈듯이, 우리는 graph에서도 FT를 이용해서 frequency space로 보낼 수 있다. 우리는 이를 graph FT라고 부르고자 하며, 이를 위해서는 graph에서 정의되는 orthonormal basis가 필요하다. 기존의 FT에서는 $e^{j\omega t}$라는 Fourier basis를 이용해서 transformation을 수행했다. 여기서 $e^{j\omega t}$는 서로 orthogonal한 성질을 지니고 있다. 그렇다면 이러한 basis를 graph에서 어떻게 정의할 수 있을까?

Graph에서의 basis를 정의하기 이전에 graph에 대해서 조금 더 알아보고 넘어가도록 하자. 일반적으로 graph는 adjacency matrix $A$로 나타낼 수 있다. $A$는 square matrix이고 각 element $a_{m,n}$은 connectivity information을 나타낸고, $a_{m,n}$은 $E$ 혹은 $\omega$에 해당한다. 일반적으로 각 entry는 0 아니면 1을 나타내어 binary adjacency matrix를 구성하며, 만약 $\omega$에 대응하게 된다면 각 edge weight 값이 0과 1 대신에 표기될 것이다. 어느 경우든 간에 adjacency matrix $A$를 통해서 graph를 나타낼 수 있다.

또 다른 matrix로 degree matrix $D$가 존재한다. $D$ 또한 square matrix로 각 diagonal은 edge weight의 sum으로 구성되어 있다. 우리는 $A$와 $D$를 이용해서 또 다른 operator인 graph Laplacian $L$을 구성할 수 있다. $L$은 두 matrix의 차이로 만들 수 있으며, graph Laplacian에서 Laplacian이라고 불리는 이유는 $L$을 graph의 node에서 정의된 signal $f(m)$에 곱했을 때 이웃하는 node간 차이가 구해지게 되고, 여기에 weight를 곱하고 전부 더하게 되면 이러한 결과가 이웃간 차이를 계산하는 기존의 Laplacian 수식과 매우 유사하게 되기 때문이다.

위의 a와 같이 별 모양의 graph가 주어지게 되면 adjacency matrix는 b처럼 주어지게 된다. 연결된 edge를 노란색으로 표기한다고 하면 첫번째 node의 경우 3번째와 4번째 node와 연결되어 있음을 matrix $A$를 통해서 확인할 수 있다. 첫번째 row가 첫번째 node에 해당하고 3번째, 4번째 column이 0이 아니기 때문에 3번째, 4번째 node와 연결되었음을 의미한다. (1,3), (1,4)로 해석할 수 있고, 각각의 index에 대응하는 node가 연결되어 있는 것이다. 이런식으로 두번째 node가 4번째와 5번째 node와 연결되어 있음을 확인할 수 있다. 따라서 adjacency matrix는 connectivity 정보를 담고 있으며, 여기서 각 row를 전부 더해서 diagonal matrix로 구성하면 이것이 바로 degree matrix $D$이다. 현재 예시를 들고 있는 별 모양의 graph는 모든 node가 2개의 node만을 연결하고 있기 때문에 $D$의 diagonal entry는 모두 2가 될 것이다.

마지막으로 $D$에서 $A$를 빼주면 graph Laplacian matrix $L$이 위와 같이 만들어지게 되고, 위의 그림에서 보다시피 square하고 symmetric matrix임을 확인할 수 있다. 그래서 여기에 우리는 eigen deocmposition을 수행해서 eigenvalue $\lambda$와 orthonormal한 eigenvector $\chi$를 얻고자 한다. $L$이 positive semi-definite한 matrix이기 때문에 eigen decomposition을 했을 때 모든 eigenvalue들이 음수인 경우는 생기지 않게 된다. 그리고 각 eigenvalue에는 이와 대응되는 eigenvector가 존재한다. 그래서 graph가 주어지면 우리는 orthonormal basis를 찾을 수 있고, 여기에 대응하는 음수가 아닌 eigenvalue들을 얻게 된다.

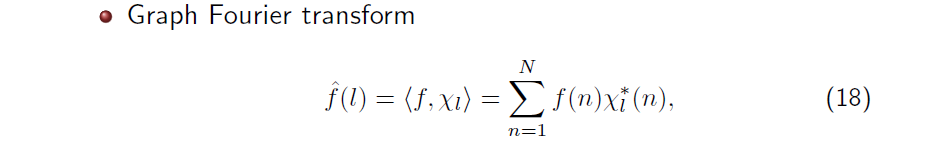이제 우리는 이렇게 얻어진 eigenvector를 이용해서 graph Fourier transformation (GFT)을 정의할 수 있다. GFT를 정의하기 위해서는 graph $G$에서 정의되는 orthonormal basis가 필요하다. 그래서 우리는 $L$의 eigenvector $\chi$를 basis로 사용해서 GFT를 정의할 것이다. GFT도 결국에는 transformation이기 때문에 inner product로 정의할 수 있다. Node에서 정의되는 signal $f$가 주어지면 $f$와 $\chi$간 inner product를 구할 수 있고, 계산을 하게 되면 graph Fourier coefficient $\hat f$를 얻을 수 있다.

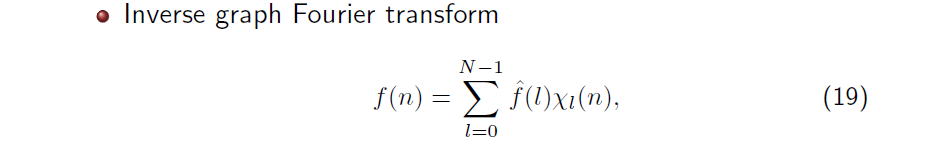그리고 이렇게 얻어진 coefficient $\hat f$를 이용하면 inverse graph Fourier transform (IGFT)를 정의할 수 있다. IGFT는 원래의 $f(n)$을 reconstruction할 수 있으며, 이는 다시 coefficient와 basis간 linear combination으로 계산이 된다. GFT와 IGFT 모두 $L$의 eigenvector $\chi$를 이용해서 transformation이 수행이 되는 것을 볼 수 있다.

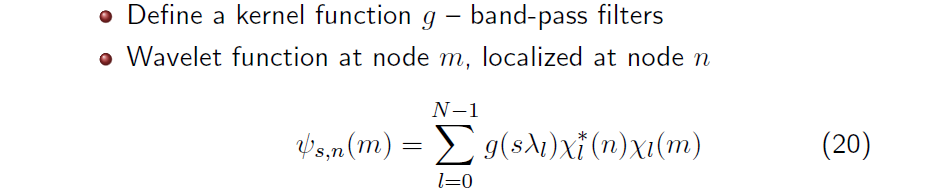이제 GFT를 알았기 때문에 우리는 한발 더 나아가 graph wavelet transformation (GWT)를 정의할 수 있다. 우리가 GWT를 정의하기 위해서 해야하는 것은 frequency space 상에서 band-pass filter로서 역할을 하는 kernel function $g$를 정의하는 것이다. Wavelet transformation은 요약하면 Fourier coefficient를 filtering하고 inverse transformation을 하는 과정이었다. 우리는 GWT을 이러한 식으로 정의할 수 있으며, 이는 마찬가지로 정확히 WT가 band-pass filtering과 동일하게 정의가 된다.

GWT를 하기 위해서 우리는 먼저 delta function $\delta$에 WT를 수행해서 wavelet basis를 만들 수 있다. Graph의 경우에는 $\delta_n$이 node $n$에서 정의가 되며, $\delta_n$과 eigenvector $\chi_l$간 inner product를 계산해주면 $\sum_{m=1}^N\delta_n(m)\chi_l^*(m)=\chi_l^*(n)$이라는 결과를 얻을 수 있다. 이 식에서 $\delta_n(m)$은 $m=n$인 경우에만 1이 될 것이라서 간단하게 $\chi_l^*(n)$을 이끌어낼 수 있게 된다. Graph space에서 delta signal도 time space와 마찬가지로 graph frequency space 상에서 특정 값을 나타내게 된다. 우리는 time space에서의 delta signal이 frequency space 상에서 특정 constant로 표현되는 것을 알고 있다. 따라서, $\chi_l^*(n)$도 GFT를 이용해서 $\delta_n$을 frequency space로 transformation 시킨 결과이다. 우리는 delta signal을 frequency space로 transformation함으로써 wavelet basis를 만든 것이고, 이는 band-pass filtering을 수행하는 것과 완전히 동일하다.

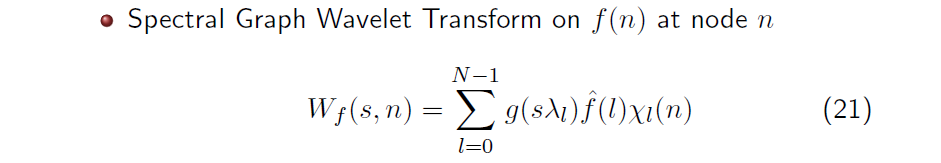이제 우리는 식 20에서 구한 mother wavelet $\psi_{s,n}(m)$을 이용해서 GWT를 수행할 수 있다. Continuous WT을 생각해보면 원래의 signal과 basis간 inner product를 수행하면 된다. Node $n$에서 $f(n)$이 주어졌을 때 우리는 $f$와 $\psi$간 inner product를 통해서 위와 같이 spectral GWT (SGWT)를 수행할 수 있고, 이를 통해서 node $n$에 대한 wavelet coefficient $W_f(s,n)$을 얻을 수 있다. $W_f(s,n)$은 filter $g(s\lambda_l)$과 graph Fourier coefficient $\hat f(l)$, 그리고 basis $\chi_l(n)$을 모든 N개의 eigenvector에 대해서 inner product를 취해서 구할 수가 있다.

Summary

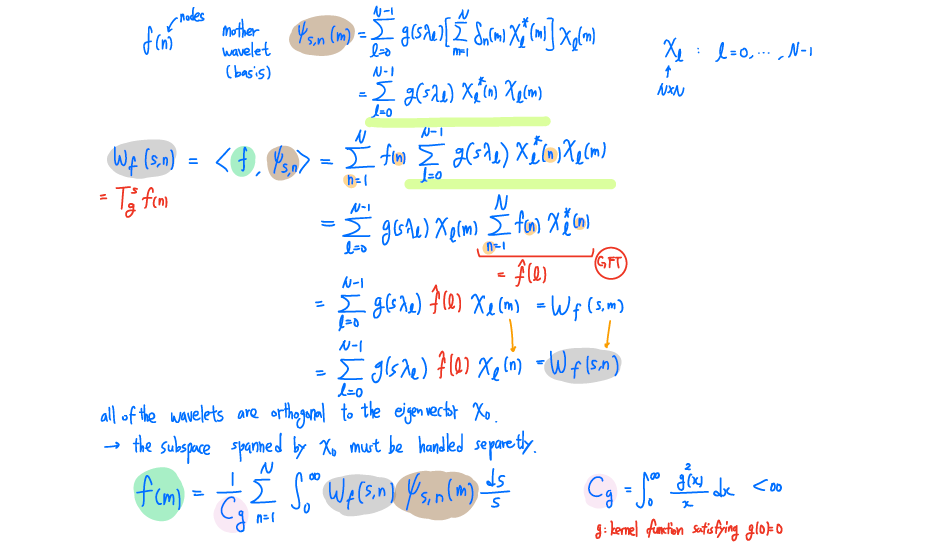
Interpretation

우리는 이렇게 WT를 통해서 얻은 wavelet coefficient를 어떻게하면 쉽게 이해할 수 있는지 생각해볼 필요가 있다. 우리가 transformation에 사용하는 filter의 경우 low frequency를 통과시킬 수도 있고, 반대로 high frequency를 통과시킬 수도 있다. 그리고 이러한 filter에 사용되는 scale의 크기에 따라서도 어떠한 결과를 얻을지 정할 수가 있을 것이다. 결국 어떠한 frequency를 포착하고 어떠한 scale을 사용해서 얻어진 wavelet coefficient가 어떠한 의미를 가지는지 알아야 우리가 원하는대로 filter를 설계해서 분석할 것이다. 우선 기본적으로 scale의 경우 클수로 넓은 영역을 분석한다고 생각하면 된다.

Low-pass filter

Low-pass filter의 경우 graph에서 low frequency를 강조하며, 이는 global한 information이나 전반적인 flow를 반영하게 된다. 이러한 filter를 사용하면 graph에서 넓은 범위의 전체적인 패턴을 잡아내고, node간 전반적인 similarity를 강조할 수 있다. Low-pass filter를 사용하는데 scale이 큰 경우에는 graph 전체에 걸친 매우 넓은 영역의 signal 변화를 분석하게 된다. 반대로 작은 scale의 경우에는 부분적인 signal을 포착하게 되어, 국소적으로 여러 이웃과 비슷한 성향을 가지는지 여부를 분석하게 된다. 요약하면 graph에서 전역적인 흐름이나 평균적인 signal의 특성을 포착하는 데 유용하며, 큰 scale에서 중요한 노드는 전체적인 패턴을 반영하고, 작은 scale에서는 국소적인 평균적 흐름을 분석한다.

High-pass filter

High-pass filter는 graph에서 high frequency를 강조하며, 이는 local한 information이나 부분적인 변화를 포착하게 된다. 이러한 filter는 node간 급격하게 변하는 신호를 포착해서 graph의 미세한 구조나 경계 영역을 분석하는데 유용하다. High-pass filter에서 scale이 큰 경우에는 넓은 범위에서 발생하는 부분적인 변화를 포착하며, 이는 주로 graph에서 크고 중요한 경계부분이나 급격하게 변동하는 signal을 보이는 node를 찾게 된다. 반대로 작은 scale의 경우에는 이웃 간의 급격한 signal의 차이를 포착하게 되는데, 이는 이웃 node간 미세한 경계나 세부적인 signal의 변동을 분석할 수 있다. 요약하면 graph에서 세부적인 경계나 국소적인 변화를 포착하는 데 적합하며, 큰 scale에서는 넓은 범위의 변화 지점을, 작은 scale에서는 미세한 경계를 잡아낸다. 그리고 wavelet coefficient의 크기는 해당 node가 filter에 의해 강조된 frequency에서 얼마나 중요한 역할을 하는지를 나타낸다. 그 값이 크면 해당 frequency에서 중요한 signal의 변화를 반영하며, 그 값이 작으면 상대적으로 덜 중요하며 안정적인 영역에 해당하게 된다.

Graph Convolutional Network (GCN)

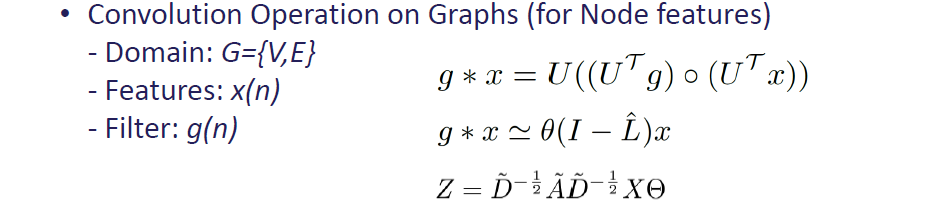WT에서 비롯된 filtering idea로부터 graph convolutional network (GCN)이 등장했다. Graph convolution은 filter $g$와 signal $x$ 사이에서 수행되며, 위와 같이 $U((U^Tg)\circ(U^T)x))$와 같이 계산될 수 있다. $g$와 $x$ 사이에서 convolution을 수행하는 것은 $x$에 filter $g$를 이용해서 filtering하는 것과 동일하게 볼 수 있다. 이러한 graph 상에서의 filtering으로부터 2017년에 kipf는 graph convolution이 위와 같이 동작할 수 있음을 수식화하였다.

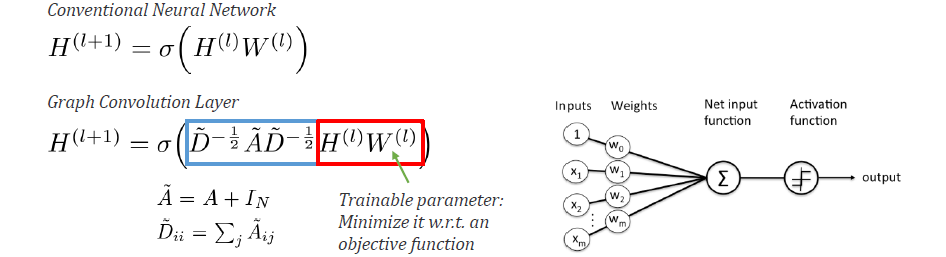일반적인 AI에 대해서 어느정도 알고 있다면 conventional neural network가 위와 같이 계산되는 것을 쉽게 이해할 수 있을 것이다. Input이 있다면 weight와 linear하게 combine 되고 summation까지 취해서 activation을 거치는 것까지가 일반적으로 동작하는 방식일 것이다. 위의 식에선 input이 $H$이고 weight가 $W$인 것이고, 이들간 linear combination 이후 activation function $\sigma$를 거쳐서 다음 layer에 input으로 들어갈 output을 만들어낸다.

Graph convolution layer의 경우에는 위와 같이 식이 정리될 수 있는데, 이는 기존의 neural network와 거의 유사한 것을 알 수 있다. 차이점이라고 한다면 기존의 input 앞에 adjacency matrix가 곱해진다는 것이다. 기존의 linear combination은 동일하지만, 앞에 graph adjacency가 곱해지면 이를 graph convolution layer라고 부르게 된다. 앞에 곱해지는 $A$의 역할은 오로지 연결된 node에 대해서만 식이 계산되도록 만들어지고, 나머지 node에 대해서는 지워버리게 된다. 일종의 feature selection을 하는 operation으로 이해해도 된다. 이렇게 하면 모든 variable을 고려하지 않고 local linear combination을 할 수 있다. 이는 graph의 connectivity 정보를 고려한 convolution으로 해석이 되는 것이다.

Filtering via Kernel

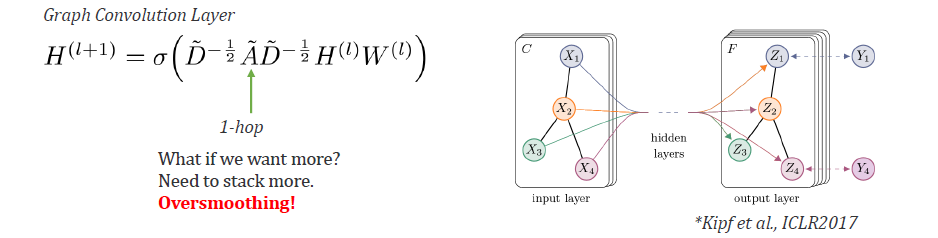하지만 이러한 operation에는 큰 문제가 존재한다. 이렇게 단순히 adjacency matrix를 곱해주게 되면 1-hop distance만을 고려하는 convolution이 수행된다. 여기서 1-hop distance라는 것은 바로 이웃한 node를 가리키기도 하며, 1번 점프를 했을 때 바로 옆의 node로 이동함을 의미하게 된다. 그래서 2-hop 이상 멀리 떨어진 node에 접근하기 위해서는 점프를 여러번 해야하며, 이는 layer를 깊게 쌓아야 하는 문제를 발생시킨다. 그렇다면 layer를 깊게 쌓는 것이 왜 문제가 되는 것일까? Layer를 깊게 쌓는 것은 그만큼 $A$를 여러번 곱하게 되는 것을 의미한다. 이는 모든 node에 대해서 각각 이상적인 hop distance가 있을텐데 이를 무시하고 여러번 점프를 진행시키게 만들고, 이렇게 정보가 계쏙해서 누적이 되다보면 oversmoothing 문제가 발생하게 되어 모든 node들이 특징적이지 않고 비슷한 정보를 가지도록 평균화가 진행될 것이다.

이러한 문제를 해결하기 위해서 각 node마다 동일한 hop distance 대신에 특정한 range를 볼 수 있도록 만들 수가 있다. 여기서 range는 kernel function $e^{-s\lambda}$로 정의될 수 있고, 이는 heat diffusion equation으로 물리학에서 비롯된 개념 중 하나이다. Kernel $h_s(p,q)$는 location $p$에 있는 경우 diffusion distance가 무엇이며, $p$에서 scale $s$로 energy를 퍼트리면 $q$까지 얼마나 걸리는지를 나타낸다. 우리는 이를 random walker distance라고 표현하기도 한다. 만약 술을 많이 마셔서 취한 사람의 경우 본인조차 어디로 갈지 잘 모르는 것이 대부분일 것이다. 이렇듯 임의로 걷고 있는 것과 유사한 상황임을 알 수 있다. 그리고 이러한 상황에서는 어디로 걷는지 모르면서 동시에 몇분동안 얼마나 걸을지도 모를 것이다. 어디로 얼마만큼의 시간동안 갈지를 우리는 정의할 수 있고 이것이 $h_s(p,q)$의 행동을 설명하게 된다. 현재 위치 $p$에서 얼마만큼의 $s$ 시간이 흐른 뒤에 $q$에 도착할지를 설명하는 개념인 것이다. $h_s$를 통해서 negiborhood의 local range를 정의할 수 있고, 이러한 range를 통해서 기존의 hop distance를 재정의할 수 있는 것이다.