[기계학습] Parametric Density Estimation - Bayesian Inference

Bayesian Inference

MLE같은 경우 우리가 관찰하는 결과에 따라 그 값이 너무 민감하게 변화하여 주어진 data들만 잘 설명하고, MAP의 경우 관찰할 수 있는 data 외에도 적절한 data가 있다면 관찰한 data만을 사용하는 것보다 더 우수하게 parameter를 추정할 수 있다. Bayesian inference는 MLE와 MAP와는 다른 방법으로, model parameter를 추정하고자 할 때 가장 근본이 되는 학습에 사용되는 방법이다. Model parameter $\theta$를 추정하고 random variable의 expected value와 variance를 구하는 등 동일한 작업을 MLE와 MAP에서도 할 수 있지만 여기에는 다소 한계점이 존재한다. MLE, MAP도 parameter를 추정하고자 사용되고 이후 posterior distribution이나 likelihood distribtuion을 최대로 만들 수 있는 좋은 방법이지만 계산하는데 있어서 더 직관적인 방법이 필요했던 것이다. MLE, MAP는 보통 2-step으로 먼저 parameter를 추정하고 관심있는 특정 값을 구하게 되는데 이 과정이 다소 복잡하다는 것이 Bayesian inference를 사용하는 이유이다.

또 다시 동전 던지기를 예시로 들어서 총 10번의 시도를 통해서 앞면이 7번 나온 상황을 볼 것이다. 이때 MLE를 통해서는 0.7의 앞면이 나올 확률을 구했으며, MAP를 통해서는 prior를 추가함으로써 0.7보다 더 작은 확률을 구해서 좀 더 0.5에 가까운 값을 제시할 수 있었다. 그러나 여기에는 우리의 불확실성에 대한 이해와 계산이 전혀 들어가있지 못하다. 여기서는 likelihood가 어떻게 보이는지 알 수는 없지만 0.7에서 그저 최대를 만족하게 된다는 사실만 인지하게 된다. 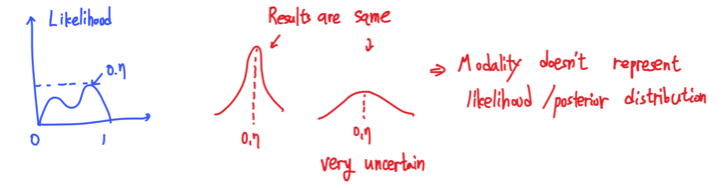만약 파란색 그래프와 같은 모양의 likelihood distribtuion을 가진다고 했을 때 물론 0.7에서 최대를 만족한다고 할 수 있다. 혹은 model이나 sample에 따라서 빨간색 그래프와 같은 estimation 결과를 가질 수도 있다. 이때 모두 0.7에서 최대를 만족하는 estimation 결과를 가지게 되지만 사실 이 구간 외에는 정확히는 어떠한 상태인지는 알 수가 없는 것이다. Likelihood나 posterior를 구하는데 있어서 불확실성은 존재하게 되지만 이를 대놓고 표현하지 못하기에 MLE나 MAP가 어느정도 한계점이 존재하는 것이다. 그래서 우리는 MLE와 MAP를 사용해서 추정한 결과에 대해서 불확실성이 존재하기 때문에 무조건 확신할 수는 없다.

MLE/MAP vs Bayesian Inference

이러한 불확실성에 대한 issue를 해결해줄 수 있는 것이 바로 Bayesian inference이다. 새로운 data point $x_\text{new}$의 distribtuion $p(x_\text{new}|\mathcal{D};\alpha)$을 추정하기를 원한다고 해보자. 그러면 MLE와 MAP는 model parameter $\hat{\theta}$를 추정해서 distribtuion $p(x_\text{new}|\hat{\theta})$을 구하게 될 것이다. 그리고는 이렇게 구한 $p(x_\text{new}|\hat{\theta})$를 사용해서 $x_\text{new}$를 설명하려고 노력할 것이다. 그러나 사실 이 방법은 $p(x_\text{new}|\mathcal{D};\alpha)$를 추정하는데 있어 매우 간접적인 방법이다. 우리가 원하는 것은 우리가 관찰한 것이 주어졌을 때 우리가 추정하고자 하는 것의 conditional probability이다. 그러나 MLE와 MAP에서는 우리의 관찰 결과인 $\mathcal{D},\alpha$를 parameter $\hat{\theta}$로 요약되어 설명하려고 한다. 그래서 MLA와 MAP는 우리의 관찰을 그저 근사시키는 정도가 되며, Bayesian inference에서 우리가 하고자 하는 것은 결국 conditional distribtuion $p(x_\text{new}|\mathcal{D};\alpha)$를 직접 추정하고자 하는 것이다. 이는 어떻게 할 수 있을까?

추정하고자 하는 conditional probability를 law of sum에 의해서 식을 다시 적을 수 있다. 이는 marginalization을 한다고 생각하면 되고, 이를 통해서 식을 분해할 수가 있다. 그러면 분해한 식을 다시 간단하게 적을 수가 있는데, 여기서 중요한 점은 data에 대한 정보들은 걸러질 수 있다는 것이다. 왜냐하면 $\theta$는 새로운 data point를 만들어내는 것과 관련이 있어서 data point를 잘 설명할 수 있다. 비록 또 다른 data들을 관찰한다고 해도 이는 전혀 상관이 없기 때문에 결국에 $p(x_\text{new}|\theta,\mathcal{D};\alpha)$는 간단하게 $p(x_\text{new}|\theta)$로 다시 적을 수가 있는 것이다.

그럼 이렇게 정리된 식을 보면은 우선 $p(\theta|\mathcal{D},\alpha)$는 MAP에서 계산했던 것과 같은 posterior distribution이다. 이렇게 식을 나타내게 되면 결국에 우리가 원하던 $\theta$ 불확실성을 포착할 수 있게 된다. 즉, 모든 parameter를 추정해서 사용할 수 있다는 것이다. 그래서 최대를 만족하는 parameter를 추정하는 것 외에도 모든 상황에 대한 parameter를 알게되어 전체적인 상황을 고려하여 불확실성을 없앨 수가 있다. Bayesian inference는 parameter의 특정 값을 선택하는것 대신에 $\theta$의 모든 값에 대한 weighted average를 통해 직접 추정하려고 하는 것이다.

Posterior Calculation

여기서 계산할 때 신경써야 할 점은 바로 integral이다. 일반적으로 integral 계산은 복잡하여 신경을 많이 써줘야 한다. 이는 posterior과 likelihood가 어떻게 생겼는지에 따라 매우 의존적이게 된다. 다행히도 integral의 계산에 있어 likelihood와 prior의 적절한 조합들이 존재하고, 이러한 조합들을 conjugate prior라고 한다. Integral 안에는 likelihood $p(x_\text{new}|\theta)$와 posterior $p(\theta|\mathcal{D},\alpha)$의 곱셈 형태로 되어 있지만, 사실 이 식은 계산하기 쉽게 식을 다시 나타낼 수가 있다. 왜냐하면 posterior distribtuion을 다음과 같이 계산할 수 있기 때문이다. 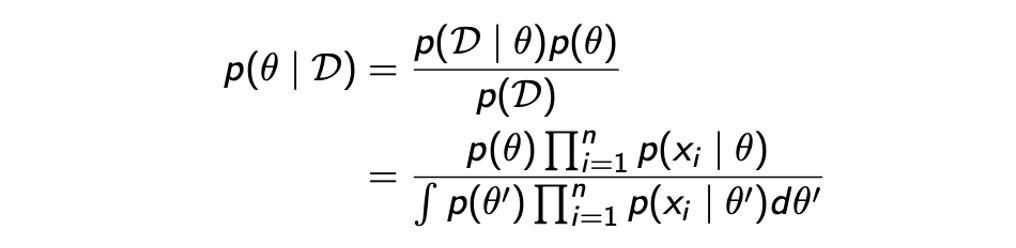$\theta$의 posterior distribtuion은 Bayes' theorem에 의해서 나타낼 수 있으며, 여기서l likelihood는 i.i.d.를 만족하게 되어 위와 같이 나타낼 수 있다. 결국 posterior를 또 다른 likelihood로 분해할 수 있기 때문에 결과적으로 integral을 계산하는데 있어서 다루기 쉬워지게 된다.

Some Conjugate Priors

다음은 $p(x_\text{new}|\theta)p(\theta|\mathcal{D},\alpha)$의 계산을 좀 더 쉽게 만들 수 있는 조합들을 나타낸 것이다.
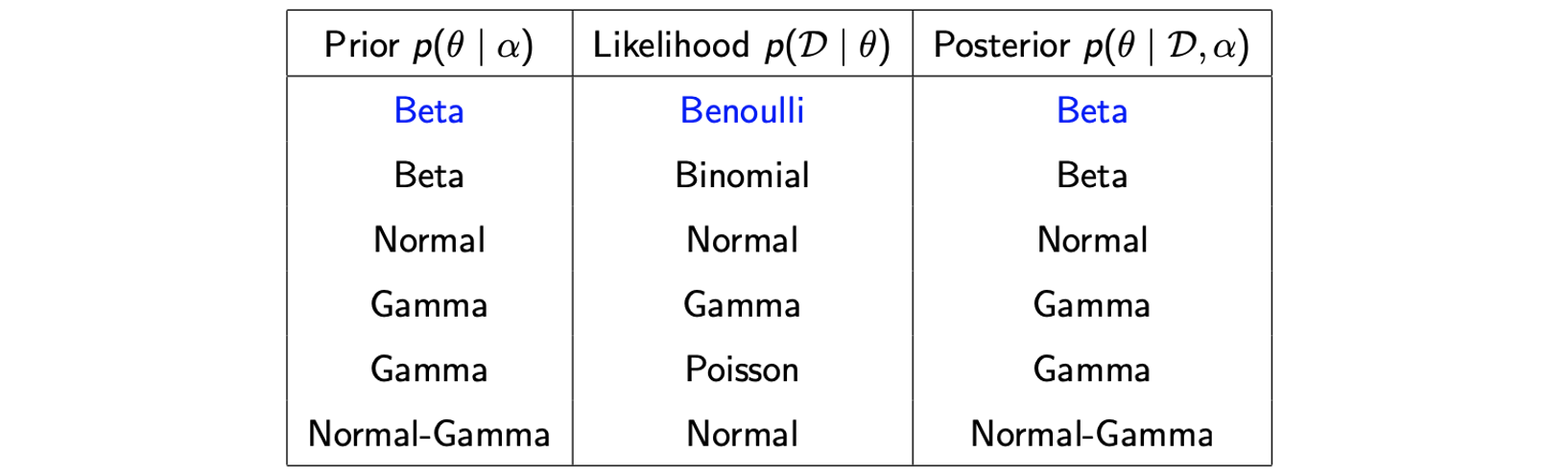예를 들어 prior가 Beta distribution이고, likelihood가 Bernoulli distribtuion인 경우에 posterior는 Beta distribtuion이 되며, 계산이 간단해진다. 그래서 일반적으로 prior가 conjugate prior라고 한다면 likelihood를 선택할 수 있는 대안들이 주어지는 것이다. Beta distribtuion을 Bernoulli나 Binomial likelihood의 conjugate라고 할 수 있는 것이다.

Example of Bayesian Inference

Example 1: Beta-Bernoulli-Beta

Example 2: Normal-Normal-Normal

우리의 model(likelihood)는 $n$개의 $x_i$의 sample로 이루어진 dataset $\mathcal{D}=\{x_i\}_{i=1}^n$에 대해서 $x_i$가 i.i.d.를 만족하여 독립적으로 $\mathcal{N}(\mu,\sigma^2)$을 따른다고 할 것이다. Prior에서 $\sigma^2$는 이미 알려진 값이고 추정해야 하는 $\mu$는 $\mathcal{N}(\mu_0,\sigma_0^2)$를 따르고 있기엔 여기서의 density function은 $p_0(\mu;\mu_0,\sigma^2)$에 의해 나타나게 된다. 즉, prior도 Normal distribtuion이고 likelihood도 Normal distribtuion인 상황이다.

그러면 posterior는 다음과 같이 구해질 수 있다.

여기서 $p_0(\mu)$는 prior로 Normal distribtuion이고, $\prod_{i=1}^np(x_i|\mu)$는 우리의 model 혹은 likelihood로 Normal distribtuion이다. 이로 인해 결과적을 posterior도 conjugate prior에 따라서 Normal distribtuion이 된다. 기본적인 계산을 마치게 되면 다음과 같이 정리된 posterior를 얻을 수 있다.

$n$에 0을 대입해보면 posterior distribtuion은 prior distribtuion과 동일해질 것이다. 반면, $n$이 무한대로 커지게되면 posterior mean은 MLE의 해를 통해서 얻을 수 있게 된다. 결국 우리가 이렇게 해서 얻은 posterior distribution $p(\mu|\mathcal{D})$는 $\int p(x|\mu) p(\mu|\mathcal{D}) d\mu$로 Normal X Normal의 형태가 되고, 따라서 이로부터 우리가 얻고자 하는 expectation이나 variance 등의 다른 값들을 쉽게 얻을 수 있다.