[데이터마이닝] Scoring, Term Weighting and Vector Space Model (VSM) 2

Documents as Vectors

이제 우리는 $|V|$ 차원의 vector space를 가지게 되었고, 이를 분석해보면 term들은 space에서 axis들에 해당하고 document는 이러한 space에서 point나 vector에 해당하게 된다. 그리고 term의 개수에 따라서 차원이 매우 커질 수가 있는 것이다. 이렇게 되면 각 vector는 매우 sparse한 vector가 되고, 대부분의 entry는 0이 될 것이다.

Queries as Vectors

이러한 이유 때문에 text analysis가 어려운 것이다. 우리는 query와 document pair로부터 score를 구할 수 있었다. 여기서 query와 document가 모두 vector라면 쉽게 score를 구할 수가 있다. 하지만 web search를 생각해보면 문제가 발생할 수 있다. Query가 vector로 주어지고 document가 매우 많이 존재한다고 했을 때, 우리는 document들을 해당 query와의 proximity를 통해서 순서를 정해줘야 한다. Vector space에서 proximity를 구한다는 것은 vector들 사이의 similarity를 구하는 것과 같다. 이는 우리가 distance의 inverse를 구하는 것과 같아지게 된다. 매우 높은 차원에서 query와 document가 있다고 했을 때, 이 둘의 거리가 가깝다는 것은 이 둘이 매우 비슷하다는 것을 의미하게 된다. 반대로 둘이 멀리 떨어져있다는 것은 이 둘이 비슷하지 않다는 것이다. 그래서 similarity는 distance의 inverse로 정의할 수 있는 것이다.

Formalizing Vector Space Proximity

그렇다면 이러한 proximity를 어떻게 정의하면 좋을까? 가장 일반적으로 Euclidean space에서 2개의 point 사이의 distance를 생각해보자. 이 방법은 그리 좋은 방법이 아닐 것이다. 그 이유는 Euclidean distanc는 서로 다른 길이를 가지는 vector들에 대해서는 큰 값을 가지기 때문이다. 단어들이 형성하는 space에서 vector의 길이가 길다는 것은 그만큼 많은 단어들을 포함하는 document를 의미한다. 결국 Euclidean distance를 구하기 위한 vector의 크기는 vector의 길이에 따라 달라지게 된다. 그래서 Euclidean distance는 그리 좋은 아이디어는 아니다.

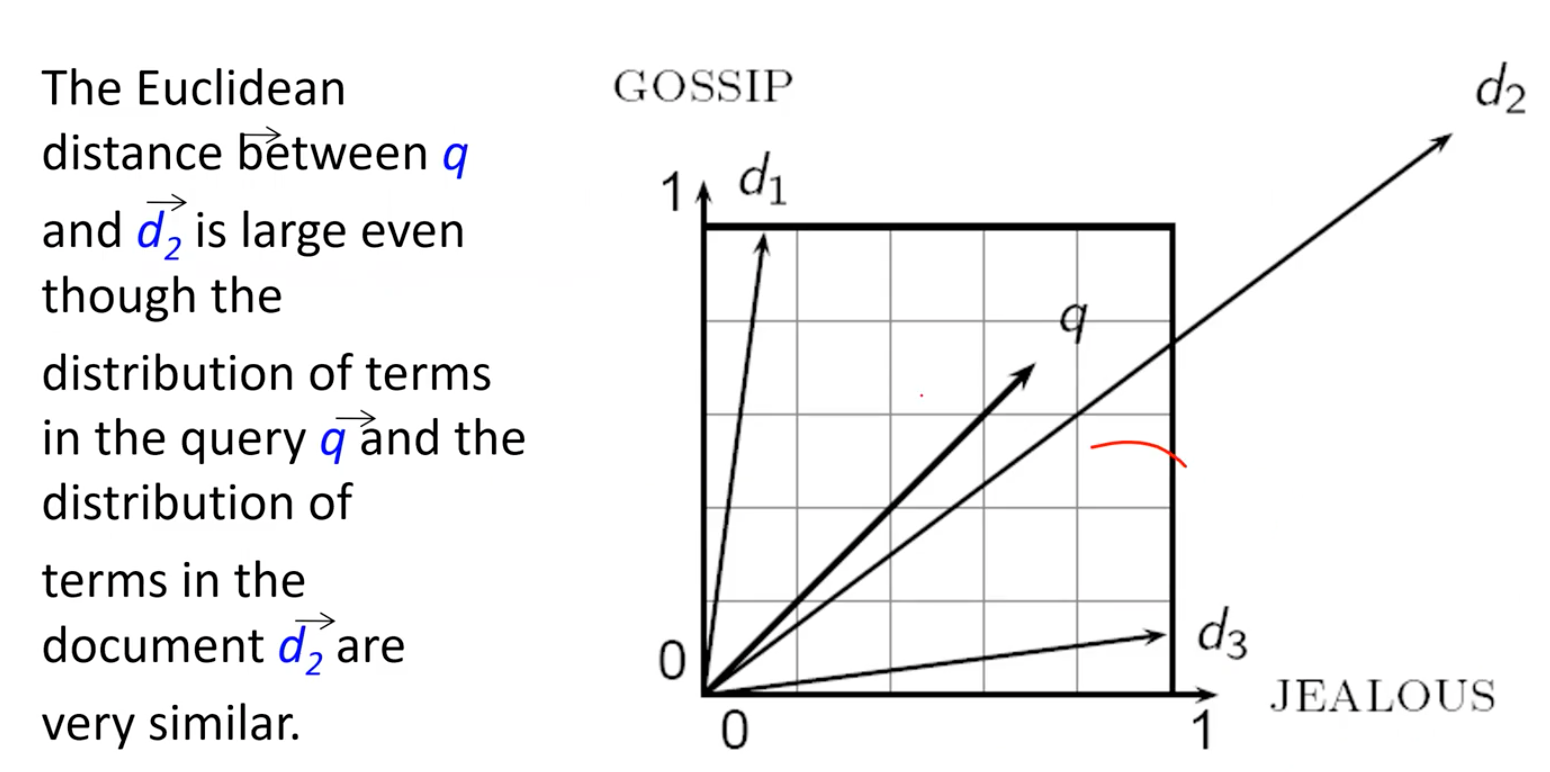
Use Angle instead of Distance

그래서 이번에는 distance 대신에 angle을 사용하고자 한다. 그리고 여기서 angle을 사용한다는 것은 결국 cosine similarity를 사용하겠다는 것과 같은 의미이다. 만약 vector space에서 document vector $d$가 있고, 이와 동일한 방향이지만 길이가 2배인 $d'$이 있다고 해보자. 그러면 이것이 의미하는 바는 동일한 내용을 복사하고 붙여넣기하여 양이 2배가 된 document가 있다는 것이다. 내용이 동일하지만 양이 다른 이러한 경우에 대해서 만약 Euclidean distance를 measure로 사용하게 되면 아마 매우 큰 값을 가지게 될 것이다. 그렇기 때문에 Euclidean distance를 사용하는 것은 좋지 못한 생각일 것이다.

하지만 만약 여기에 angle을 사용하게 되면 2개의 document 사이의 angle은 0이 될 것이고, 이는 cosine 값이 1이 되어 가장 큰 similarity를 얻을 수 있을 것이다. 그래서 cosine에 사용되는 angle이 0인 경우에는 그 값이 1이 되어 최대가 될 것이고, 반대로 angle이 1인 경우에는 그 값이 0이 되어 최소가 될 것이다.

From Angles to Cosines

위에서 보면 angle과 cosine 값의 결과가 반비례하는 경향을 볼 수 있다. 그래서 다음의 두 문장은 동일하다고 생각하면 된다.

• Rank documents in decreasing order of the angle between query and document
• Rank documents in increasing order of cosine(query, document)

이는 cosine function이 0에서 180도 사이의 구간에서는 monotonic하게 감소하기 때문이다.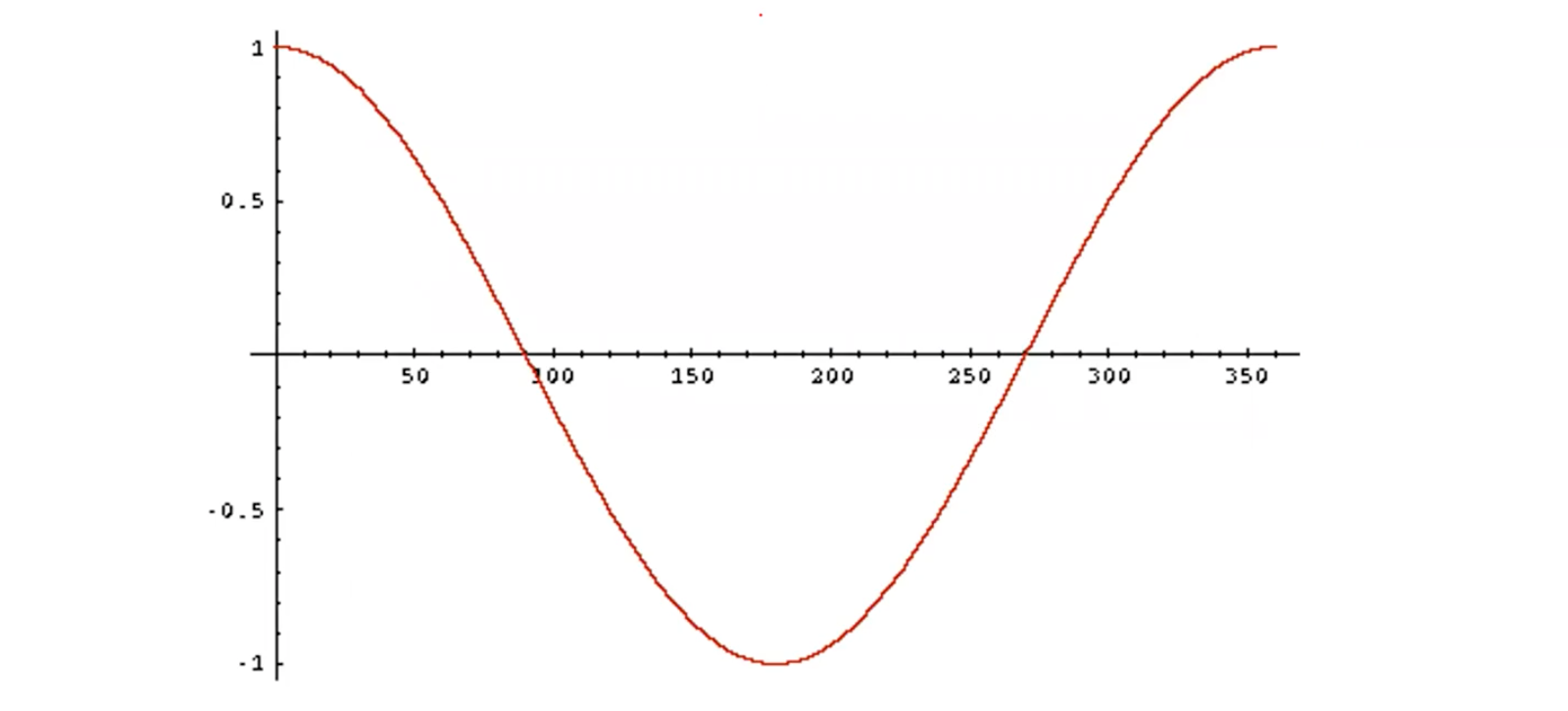

Length Normalization

Vector 연산에 있어서 inner product와 l2-norm만 알고 있으면 cosine 값을 쉽게 구할 수 있다.

우리는 vector를 l2-norm으로 나눠주게 되면 unit (length) vector로 만들 수가 있다. 위에서 document vector $d$와 $d'$이 같은 내용을 가지지만 양은 2배가 차이난다고 했다. 하지만 2개의 vector 모두 length normalization을 해주게 되면 동일한 unit vector로 만들 수가 있게 된다. 이제 normalization을 통해서 길이가 길고 짧은 document들은 서로 비교할만한 weight를 가질 수 있게 되었다.

Cosine(Query, Document)

이제 query와 document 사이의 cosine similarity는 다음과 같이 dot product와 2개의 normalized vector를 통해서 구할 수가 있다.

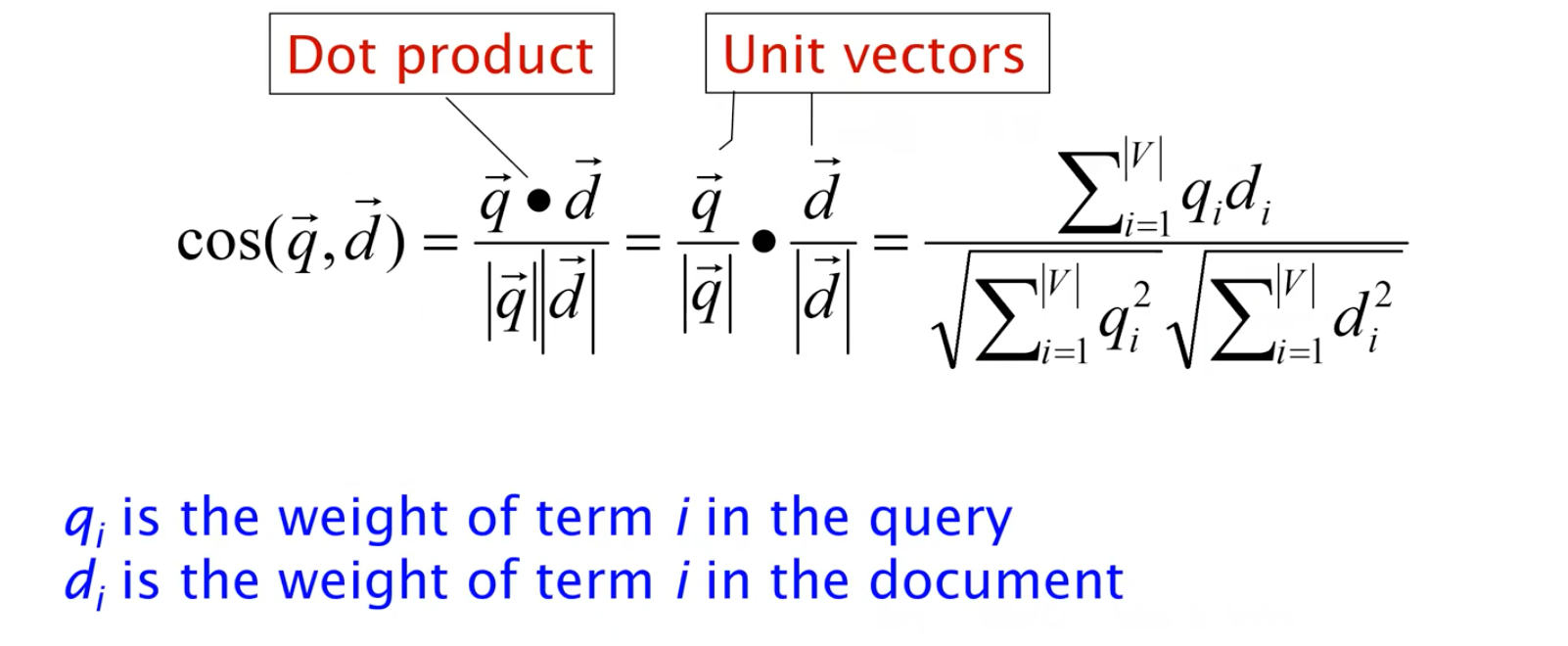
Cosine for Length-Normalized Vectors

만약 vector가 이미 length-normalized vector라면, cosine similarity는 단순히 dot product를 통해서 구할 수가 있다.

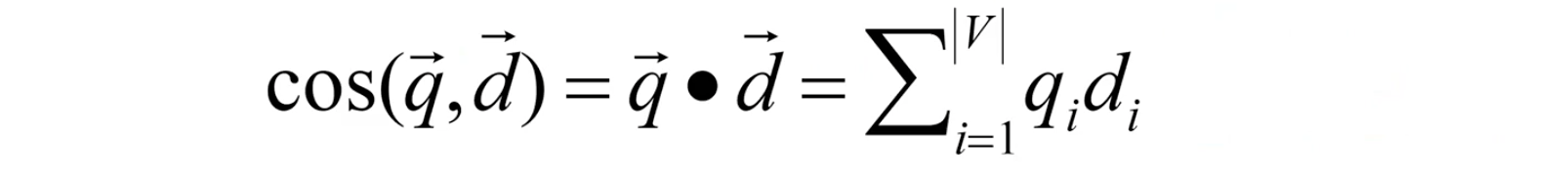
Cosine Similarity Illustrated

다음은 cosine similarity를 그림으로 나타낸 것이다.
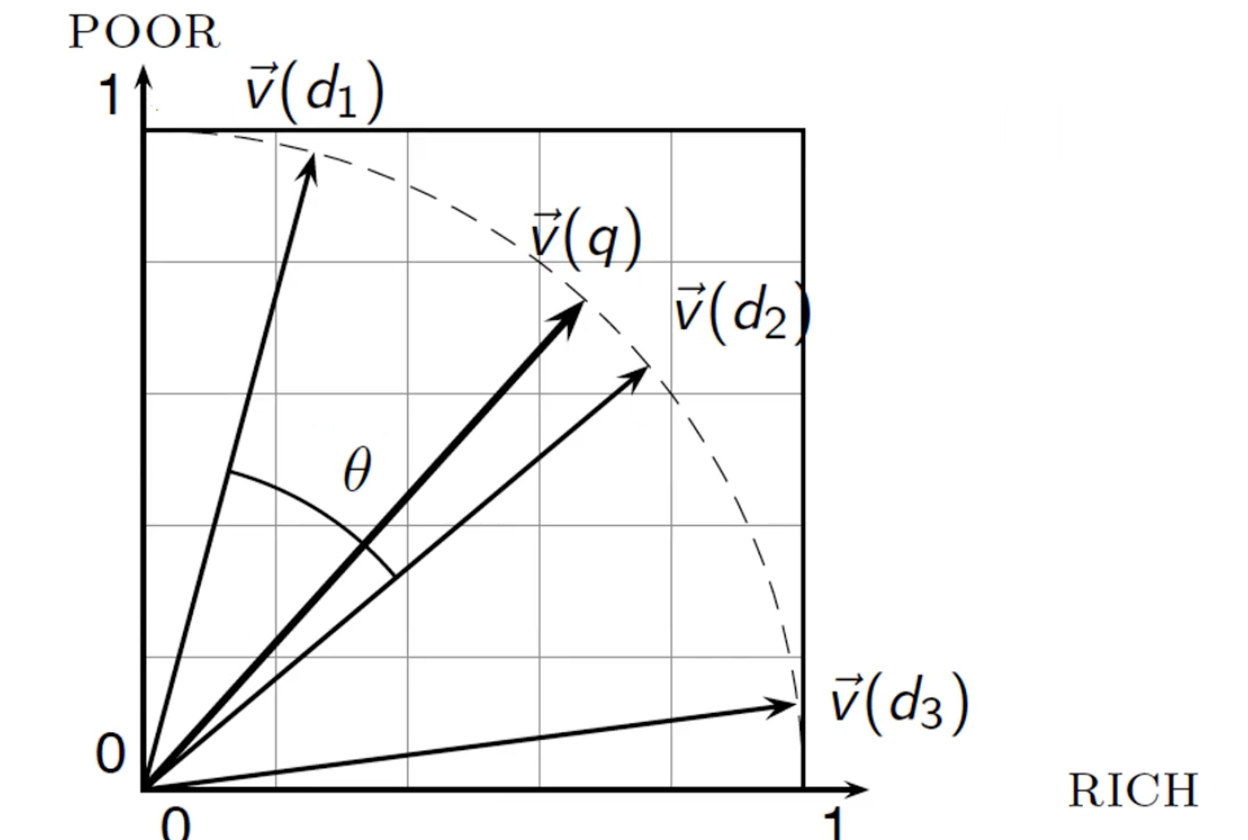모든 document vector가 unit sphere에 존재하는 것을 확인할 수 있다.

Example: Cosine Similarity amongst 3 Documents

Cosine similarity와 관련하여 예시를 보고자 한다. 위와 같이 3개의 novel SaS, PaP, WH가 있다고 해보자. 위의 novel들은 모두 어느정도 유사함이 있어보인다. 그래서 이를 확인하기 위해서 similarity measure를 이용해서 비교해보자.

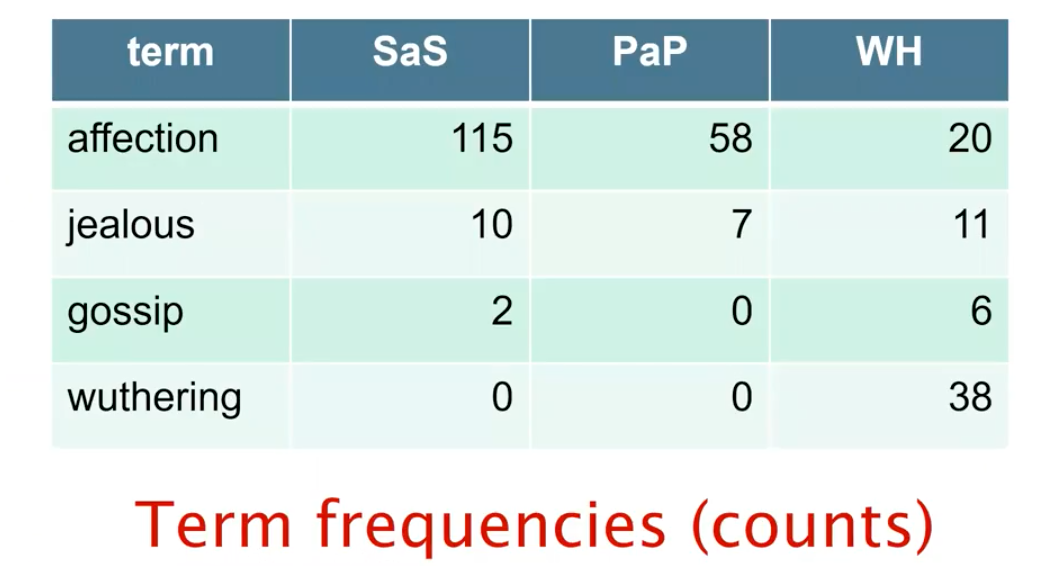총 4개의 term이 얼마나 많이 등장했는지 term frequency를 구한 것이다. 특히 jealous의 경우 WH에서 affection의 절반에 해당하지만 나머지에서는 극히 적은 tf를 보여주고 있다. 그래서 affection과 jealous의 비율이 Sas와 PaP에서는 극히 낮은 것을 확인할 수 있다. 이렇게 4차원의 vector들이 존재하는 count matrix를 통해서 어느 novel에 어느 term이 주로 등장하는지를 확인할 수 있다. 하지만 여기서 중요한 점은 각 novel마다 길이가 다르기 때문에 이를 normalization을 해줘야 한다.

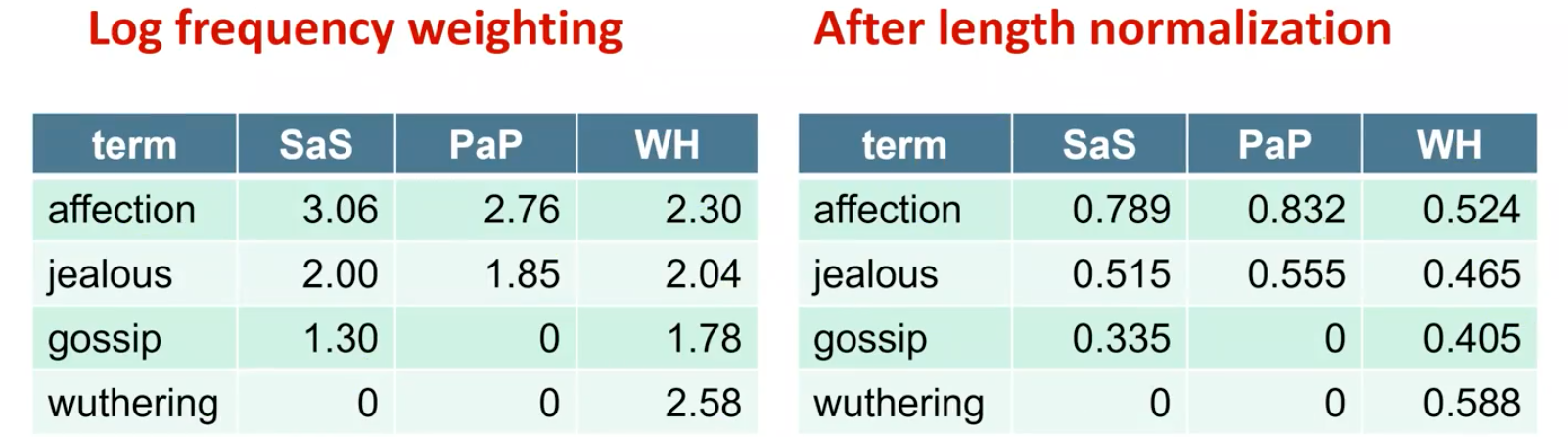먼저 log frequeny weighting 기법을 사용하면 좌측과 같은 결과를 얻을 수 있다. 그리고는 우측과 같이 length normalization을 할 수 있다. 다음과 같이 length normalization 이전에 dot product를 한 결과를 보면 서로 얼마나 유사한지 확인하기가 어렵다. 하지만 length normalization을 한 뒤에 cosine similairty를 구하게 되면 서로 얼마나 유사한지 확인할 수가 있다.
이러한 결과를 통해서 SaS와 PaP가 매우 유사한 것을 확인했다. 이를 통해서 query나 document가 서로 다른 length로 주어졌다면, 우리는 length normalization을 통해서 서로가 얼마나 유사한지를 판단할 수 있게 된다.

tf-idf Weighting has Many Variants

우리가 이번에 살펴본 tf-idf weighting 기법 외에도 다양한 변형식들이 존재한다.

Weighting may differ in Queries vs Documents

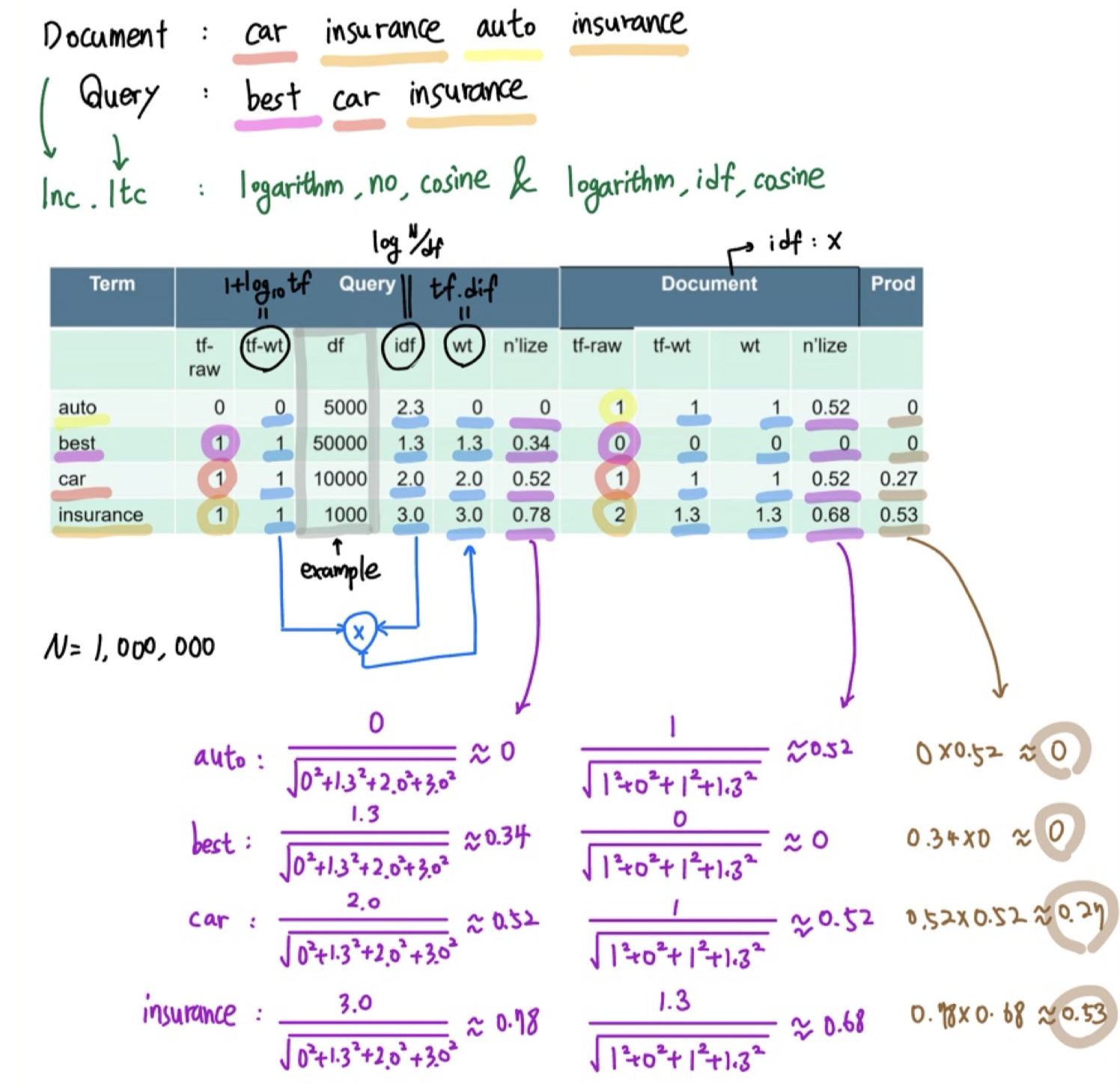
어떠한 기법을 사용하는지에 따라 ddd.qqq와 같이 term frequency, document frequency, normalization 순서대로 notation을 사용할 수 있다. Text mining 논문들을 읽어보면 이러한 표현이 자주 등장하게 된다. 가장 표준이 되는 weighting 기법은 lnc.ltc이다. 다음은 lnc.ltc 기법의 예시이다.

Summary - Vector Space Ranking

Vector space ranking에서 중요한 것은 document의 semantic이다. Query와 document가 전달하고자 하는 information이 무엇이지를 우리는 신경써야한다. 이를 효과적으로 설명하기 위해서 document를 vector space로 보냄과 동시에 이를 normalization 해야한다. 그래서 우리는 query를 weighted tf-idf vector로서 나타내야 함과 동시에 각 document 또한 tf-idf vector로서 나타내야 한다. 물론 직전 예시에서는 document를 tf vector로만 나타냈지만, 알다시피 많은 variance들이 존재한다. 여기서 중요한 점은 semantic의 관점에서 의미있는 similarity를 생각하기 위해서 query vector와 각각의 document vector 사이의 cosine similarity score를 구해야 한다. 이렇게 구한 score를 기반으로 query에 관하여 document의 순위 및 순서를 매길 수가 있다. 최종적으로 이러한 순위를 기반으로 사용자들에게 위에서부터 $K$개의 결과를 제공해주면 된다. 예를 들어 1000개의 document 중에서 순위를 매겨 10개의 결과를 제공해줄 수 있는 것이다. 이러한 방식으로 query와 각각의 document로부터 score를 구해서 순위를 매겨 사용자들에게 유용한 정보를 제공하는 것이 바로 vector space ranking 시스템이다.